Задачи на сплавы, смеси

Занятие по теме: «Задачи на смеси, сплавы, растворы».

Теоретическая

часть

Теоретические основы решения задач «на смеси, сплавы, растворы»

Терминология:

• процентное содержание вещества;
• концентрация вещества;
• массовая доля вещества .

Все это синонимы.

Определение . Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси . ( Это отношение может быть выражено либо в дробях, либо в процентах).

В данной работе чаще упоминается термин « массовая доля » .

Концентрация – это безразмерная величина. Сумма массовых долей всех компонент, составляющих смесь, очевидно, равна единице.

Рассмотрим самый распространённый тип задач, где из двух смесей (сплавов, растворов) получают новую смесь (сплав, раствор). Решим типовую задачу в общем виде, выведем формулу, а затем решим задачи с применением формулы.

Имеются два куска сплава меди с цинком. Процентное содержание меди в них p 1 % и p 2 % соответственно. В каком отношении нужно взять массы этих сплавов, чтобы, переплавив взятые куски вместе, получить сплав, содержащий p% меди?

Решение.

• Если взять два сплава, массы которых одинаковы,

т.е. m 1 = m 2 , то

• Если исходные материалы имеют одинаковую процентную концентрацию, то концентрация конечного раствора не измениться.

• Если р 1 , р 2 , р попарно не равны, то используем формулу:

• Все рассуждения верны если вместо массовой доли дается объемная доля вещества в смеси.

Практическая

часть

Задача №1. Сплав олова с медью весом 12кг содержит 45% меди. Сколько чистого олова нужно добавить, чтобы получить сплав, содержащий 40% меди.

Решение

Масса

Массовая доля чистой меди в 1-ой смеси

Масса

Массовая доля чистой меди во 2-ой смеси

Массовая доля чистой меди в общей смеси

1-ой смеси

2-ой смеси

45%

12кг

40%

0%

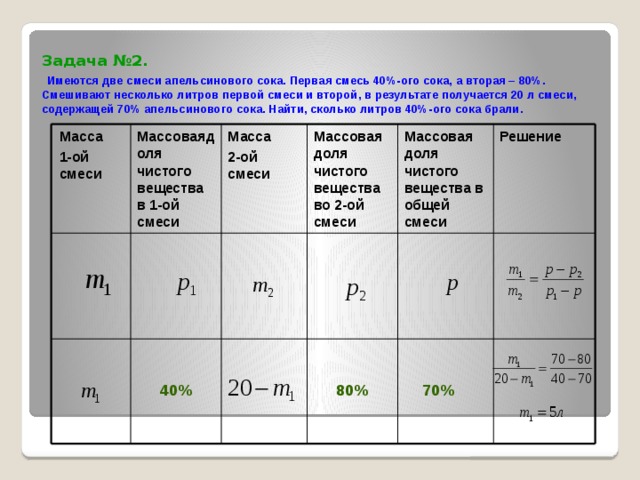
Задача №2. Имеются две смеси апельсинового сока. Первая смесь 40%-ого сока, а вторая – 80%. Смешивают несколько литров первой смеси и второй, в результате получается 20 л смеси, содержащей 70% апельсинового сока. Найти, сколько литров 40%-ого сока брали.

Решение

Масса

Массоваядоля чистого вещества в 1-ой смеси

Масса

Массовая доля чистого вещества во 2-ой смеси

Массовая доля чистого вещества в общей смеси

1-ой смеси

2-ой смеси

70%

80%

40%

Задача №3. Сколько граммов 30%-ого раствора надо добавить к 80 г. 12%-ого раствора этой же соли, чтобы получить 20%-ый раствор соли?

Решение

Масса

Масса

Массоваядоля чистого вещества во 2-ой смеси

Массовая доля чистого вещества в общей смеси

Массоваядоля чистого вещества в 1-ой смеси

1-ой смеси

2-ой смеси

80г

30%

20%

12%

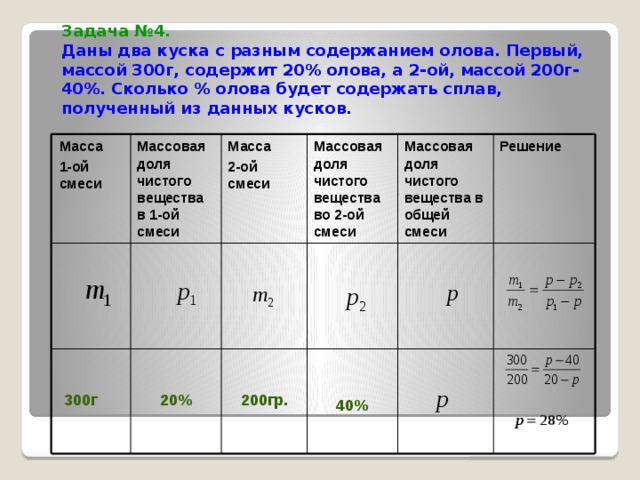
Задача №4. Даны два куска с разным содержанием олова. Первый, массой 300г, содержит 20% олова, а 2-ой, массой 200г-40%. Сколько % олова будет содержать сплав, полученный из данных кусков.

Решение

Масса

Масса

Массовая доля чистого вещества во 2-ой смеси

Массовая доля чистого вещества в общей смеси

Массовая доля чистого вещества в 1-ой смеси

1-ой смеси

2-ой смеси

200гр.

300г

20%

40%

Задача №5. В 500 кг руды содержится некоторое количество железа. После удаления из руды 200 кг примесей, содержащих в среднем 12,5% железа, содержание железа в оставшейся руде повысилось на20%. Определите, сколько процентов железа осталось ещё в руде.

Решение

Масса

Массовая доля чистого вещества в 1-ой смеси

Масса

Массовая доля чистого вещества во 2-ой смеси

Массовая доля чистого вещества в общей смеси

1-ой смеси

2-ой смеси

300кг

12,5%

200кг

Задача №6. Арбуз весил 20 кг. и содержал 99% воды, когда он немного усох, то стал содержать 98% воды. Сколько теперь весит арбуз?

Решение

Масса

Массовая доля чистого вещества в 1-ой смеси

Масса

Массовая доля чистого вещества во 2-ой смеси

Массовая доля чистого вещества в общей смеси

1-ой смеси

2-ой смеси

98%

100%

99%

Задача №7. В свежих яблоках 80% воды, а в сушеных – 20%. На сколько процентов уменьшается масса яблок при сушке?

Решение

Масса

Массовая доля чистого вещества в 1-ой смеси

Масса

Массовая доля чистого вещества во 2-ой смеси

Массовая доля чистого вещества в общей смеси

1-ой смеси

2-ой смеси

100%

80%

20%

13