6 – сабак
5 – сабак үчүн тапшырма
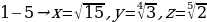
x
y
1
y
z
.
2
z
x
.
3
5x2
y8
.

4
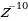
Х -10
.
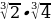
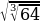
5.
6.
7
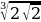
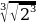
.
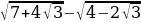
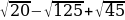
8.
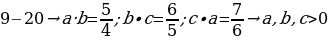
a
0
9
b
0
.
1
c
0
0.
1
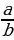
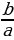
1.
1
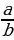
2.
1
b
- 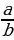
3
. 1
-a
4.
1
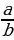
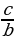
5.
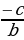
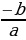
16.
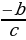
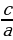
1
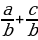
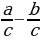
7.
18.
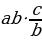
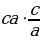
19.
2
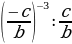
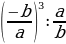
0.
21. х = a2b3 жана y = ab21 төрт орундуу сандар. Эгерде х – у = 2 болсо, b нын маанисин тап ?
1 B) 2 C) 3 D) 4 E) 5
22. a жана b – терс бүтүн сандар, жана 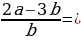 7 а + b сумма-сынын эң чоң маанисин тап ?
7 а + b сумма-сынын эң чоң маанисин тап ?
0 B) – 4 C) – 5 D) – 6 E) – 20
a,b,c – натуралдык сандар.Эгерде а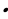 b=30 жана b
b=30 жана b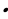 с=24 болсо,
с=24 болсо,
а + b + с нын эң кичине маанисин тап ?
15 B) 21 C) 29 D) 55 E) 61
34 жана 51 сандарынын, ЭЧЖБ 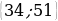 жана ЭКЖБ
жана ЭКЖБ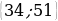 тап ?
тап ?
17 жана 51 B) 34 жана 102 C) 17 жана 102 D) 34 жана 51
E) 51 жана 1
25. 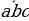 – саны 9 га бөлүнсө жана бирдиги 3 кө барабар болсо, цифралары (a
– саны 9 га бөлүнсө жана бирдиги 3 кө барабар болсо, цифралары (a b
b c) шартын канааттандыруучу канча үч орундуу сандар бар.
c) шартын канааттандыруучу канча үч орундуу сандар бар.
А) бир B) эки C) үч D) төрт E) беш
26. 5 ке бөлгөндө 3 калдык калуучу натуралдык сандын формуласы кайсы?
A)3n+5 B) 5 C) 3n-5 D) 5n+3 E) 3
2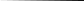 7. 95
7. 95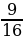 – 88
– 88 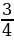 +
+ 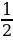
0,0001: 0,005
А) 369 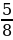 B) 365
B) 365 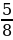 C) – 364 D) 366
C) – 364 D) 366 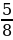 E) –365
E) –365 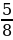
28. 500 санынын канча оң бүтүн бөлүүчүсү бар ?
A) 11 B) 12 C) 13 D) 10 E) 9
500х саны эмнеге барабар, эгерде 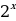 = n жана
= n жана 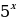 = m болсо, төмөнкүлөрдүн кимиси туура ?
= m болсо, төмөнкүлөрдүн кимиси туура ?
А) n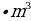 B)
B) 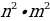 C)
C) 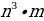 D)
D) 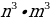 E)
E) 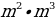
30. 2+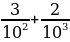 = ?
= ?
А) 2,32 B) 2,032 C) 2,303 D) 2,0032 E) 2,0302
31. а = 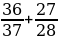 жана b =
жана b = 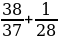 болсо, а ны b аркылуу туюнт.
болсо, а ны b аркылуу туюнт.
А) 1- b B) 2-b C) 3- b D) 1-3 b E) 3-2b
32. (1+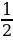 )
)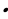 (1+
(1+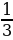 )
)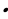 (1+
(1+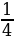 )
)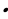 ...
...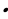 (1+
(1+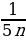 )=63
)=63
А) 20 B) 22 C) 24 D) 25 E) 29
БИР БЕЛГИСИЗДҮҮ ТЕҢДЕМЕЛЕР.
Бир белгисизди өз ичине камтыган эки туюнтмалардын барабардыгы бир белгисиздүү теңдемелер д.а.
Мейли  y = f(x) жана y = g(x) деген эки функциялар берилсин.
y = f(x) жана y = g(x) деген эки функциялар берилсин.
А көптүгү алардын жашоо аймактарынын кесилишүү аймагы болсун.
А көптүгү f(x) = g(x) бир белгисиздүү теңдемесинин жашоо областы (ТЖО) деп аталат.
f(x) = g(x) теңдемесинин тамыры деп, f(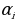 ) = g(
) = g(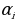 ) шартын канааттандыруучу ушундайдыр бир
) шартын канааттандыруучу ушундайдыр бир 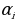 сандары аталат.
сандары аталат.
(Мында 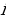 = 1,2,3, ...,п,... )
= 1,2,3, ...,п,... )
f(x)=g(x) теңдемесин чыгаруу деп, ушул барабардыкты канааттандыруучу теңдеменин жашоо областындагы х тин сандык маанилерин табууну айтабыз.
Теңдеменин тамырларынын саны, теңдеменин улуу мүчөсүнүн белгисизинин даража көрсөткүчүнүн сандык маанисинен ашпайт. Эгерде теңдеме тамырга ээ болбосо, анда анын тамырларынын көптүгү куру 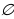 көптүк болот.
көптүк болот.
М: сызыктуу теңдеменин - бир тамыры, квадраттык теңдеменин - эки тамыры, кубдук теңдеменин – үч тамыры, 4–даражалуу теңдеменин – төрт тамыры болот.
Эки теңдеме тең күчтүү теңдемелер деп аталат, эгерде алардын тамырлары дал келсе.
Тең күчтүү теңдемелердин жашоо шарттары:
1. f(x) = g(x) 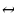 f(x) - g(x) = 0
f(x) - g(x) = 0
2. 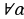 : f(x) = g(x)
: f(x) = g(x)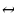 f(x)
f(x)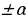 = g(x)
= g(x)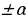
3. 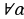 : (
: (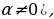 f(x) = g(x)
f(x) = g(x) 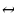 f(x)
f(x)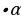 = g(x)
= g(x)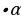 же
же
f(x) = g(x )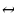 f(x)
f(x)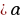 = g(x)
= g(x)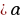 болот.
болот.
4. а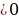 жана а
жана а 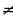 1:
1: 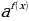 =
= 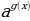
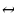 f(x) = g(x)
f(x) = g(x)
5. 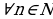 : y = f(x) жана y = g(x) функциялары терс болбосо,
: y = f(x) жана y = g(x) функциялары терс болбосо,
f(x) = g(x) 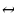 fn(x)=gn(x) болот.
fn(x)=gn(x) болот.
6. а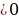 жана а
жана а 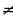 1: y = f(x) жана y = g(x) функциялары оң болсо, анда ТЖО да f (x) = g(x)
1: y = f(x) жана y = g(x) функциялары оң болсо, анда ТЖО да f (x) = g(x) 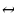 loga f(x) = logag(x).
loga f(x) = logag(x).
7. f (x) = g(x) ТЖО да y = h(x) функциясы жашап жана нөлдөн айрымалуу болсо: f(x) = g(x) 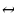 f (x)
f (x)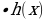 = g(x)
= g(x)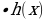 же f(x) = g(x)
же f(x) = g(x) 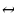 f(x)
f(x)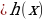 = g(x)
= g(x)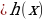 болот.
болот.
2.Бир теңдеме экинчи теңдеменин натыйжасы болуу шарттары:
Эгерде 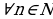 болсо, fn(x) = gn(x) теңдемеси f(x) = g(x) теңдемесинин натыйжасы болот.
болсо, fn(x) = gn(x) теңдемеси f(x) = g(x) теңдемесинин натыйжасы болот.
2. Эгерде а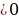 жана а
жана а 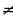 1 болсо, f(x) = g(x) теңдемеси
1 болсо, f(x) = g(x) теңдемеси
logaf(x) = logag(x) теңдемесинин натыйжасы болот.
f(x) = g(x)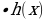 теңдемеси, f(x)
теңдемеси, f(x)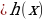 = g(x) теңдемесинин натый-жасы болот.
= g(x) теңдемесинин натый-жасы болот.
Сызыктуу теңдемелер
a∙x + b = c∙x + d - түрүндөгү теңдеме сызыктуу теңдеме болот, бул теңдемени чыгарууда белгисизи бар мүчөлөрүн барабардыктын бир жагына, ал эми турактуу сандарды барабардыктын экинчи жагына чогултабыз жана a ∙ x − c ∙ x = d – b → ( a − c) ∙ x = d – b → x = 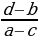 тамырына ээ болобуз ( мында а – с
тамырына ээ болобуз ( мында а – с 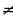 0 болуусу шарт).
0 болуусу шарт).
Квадраттык теңдемелер
а∙х2 + в∙х + с = 0 түрүнө келүүчү теңдемелер квадраттык теңдемелер болот, квадраттык теңдемелер толук, толук эмес жана келтирилген квадраттык теңдемелер болуп бөлүнүшөт.
а∙х2 + в∙х + с = 0 теңдемеси 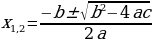 тамырларына;
тамырларына;
а∙х2 + 2к∙х + с = 0 теңдемеси 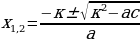 тамырларына;
тамырларына;
а∙х2 + в∙х = 0 теңдемеси х1 = 0, х2 = −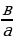 тамырларына ;
тамырларына ;
а∙х2 + с = 0 теңдемеси х1,2 = ±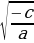 тамырларына ээ болот,
тамырларына ээ болот,
эгерде а,с сандары бирдей бегидеги сандар болсо,
ал эми карама – каршы белгиде болсо чыгарылышы жок болот;
x2 + p∙x +q = 0 теңдемеси x1,2 = −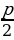 ±
±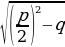 тамырларына ээ болушат. Мындан жогорку даражалуу теңдемелер бош мүчөсүнүн жөнөкөй көбөйүүчүлөрүнө жараша тамырларга ээ болот.
тамырларына ээ болушат. Мындан жогорку даражалуу теңдемелер бош мүчөсүнүн жөнөкөй көбөйүүчүлөрүнө жараша тамырларга ээ болот.
Келтирилген квадраттык теңдеменин тамырлары белгилүү болсо, коефиценттерин же системанын жардамында теңдеменин тамыр-ларын табуу үчүн Виеттин теормасы колдонулат.
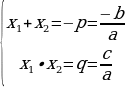 (Виеттин теормасы).
(Виеттин теормасы).
Урматтуу тестке даярдануучулар:
Тесттеги теңдемелерди чыгаруудан мурда анын жашоо областын таап, андан жооптордогу бир эле тамыр ал областка кирбей калса аны теңдеменин өзгөрүлмө чоңдугуна коюп текшерүүнүн зарылчылыгы жок, калган жоопторду текшерүү зарыл. Ошентип туура жоопту теңдемени чыгарбай эле тапса болот, бирок биз жогорудагы эрежелерди билүүбүз керек.
Мисалдар иштөө
Теңдемени чыгаргыла: 5(2 + 1,5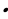 x) – 0,5
x) – 0,5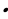 x = 24
x = 24
A) 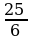 B)
B) 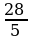 C)
C) 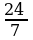 D) 3 E) 2
D) 3 E) 2
Теңдемени чыгаргыла : x+3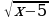 = 5
= 5
A) 5 B) 14 C) 5;14 D) –5 E) -12
Чыгаруу:
1 – жолу: Бул теңдемени чыгаруудан мурда теңдеменин жашоо областын аныктап алалы. Квадраттык тамыр жашашы үчүн х – 5 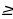 0 болуусу шарт, демек х
0 болуусу шарт, демек х 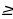 5 болот. Демек жооптогу (D), (E) шартты канаатандырбайт, теңдемени радикалдан куткарсак квадраттык теңдемеге ээ болобуз. Шарт боюнча квадраттык теңдеменин эки тамыры жашайт, биз (С) жообун теңдемеден текшерип көрсөк
5 болот. Демек жооптогу (D), (E) шартты канаатандырбайт, теңдемени радикалдан куткарсак квадраттык теңдемеге ээ болобуз. Шарт боюнча квадраттык теңдеменин эки тамыры жашайт, биз (С) жообун теңдемеден текшерип көрсөк
5 + 3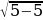 = 5
= 5 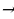 5 + 3
5 + 3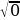 = 5
= 5 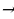 5 = 5,
5 = 5,
14 + 3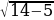 = 5
= 5 14 + 3
14 + 3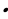 3 = 5
3 = 5 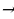 23
23 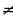 5.
5.
демек жообу (А) болот.
2 – жолу: Бул теңдемени чыгаруудан мурда теңдеменин жашоо областын аныктап алалы. Квадраттык тамыр жашашы үчүн х – 5 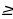 0 болуусу шарт, демек х
0 болуусу шарт, демек х 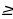 5 болот. Эми теңдемени жөнөкөйлөтөлү,
5 болот. Эми теңдемени жөнөкөйлөтөлү,
3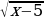 = 5 – х барабардыктын эки жагын тең квадратка көтөрсөк
= 5 – х барабардыктын эки жагын тең квадратка көтөрсөк
9 (х – 5) = 25 – 10х + х2
Мындан х2 – 19х + 70 = 0 квадраттык теңдемесине ээ болдук, бул теңдемени чыгарсак х1 = 5; х2 = 14 тамырларына ээ болобуз. Экөөбү тең шартты канаатандырат жообун (С) деп алсак болот. Ошентип биз адаштык теңдеменин тамырларын теңдемеге алып барып текшербей. Эгерде текшерсек:
х1 =5 ти коёлу: 5 + 3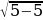 = 5
= 5 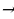 5 + 3
5 + 3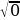 = 5
= 5 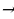 5 =5,
5 =5,
х2 = 14тү коёлу 14 + 3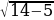 = 5
= 5 14 + 3
14 + 3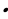 3 = 5
3 = 5 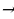 23
23 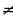 5.
5.
жообу (А) болот.
3. Теңдемени чыгаргыла : x + 2
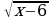 = 6
= 6
A) 3 B) 4 C) –6 D) 6 E) 7
4.Теңдемени чыгаргыла : 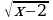 = 7 – 2x
= 7 – 2x
A) 3 B) 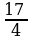 C) 1 D) -3 E) 3;
C) 1 D) -3 E) 3;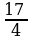
5.Теңдемени чыгаргыла : 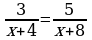
A)  B)
B) 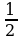 C)
C) 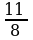 D) 2 E) 4
D) 2 E) 4
6.Теңдемени чыгаргыла : 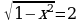
A) 0 B) –1 C) 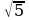 D) чыгарылышы жок
D) чыгарылышы жок
7.Теңдемени чыгаргыла : |x+5|-|x-3|=8
A) 3 B) –3 C) (-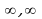 ) D) (3,
) D) (3,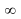 ) E) (-3,
) E) (-3,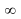 )
)
Теңдемени чыгаргыла : |2x+1|=x
A) x = 1 B) x = -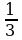 C) чыг.жок D) x1=-1; x2=2, E) x1=2, x2 = -
C) чыг.жок D) x1=-1; x2=2, E) x1=2, x2 = -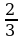
Теңдемени чыгаргыла: 7 - (3,1+ 0,1y)=4 - 0,2y
A) y=-3 B) y=3 C) y=0,3 D) y=-0,3 E) y=1
Теңдемени чыгаргыла: 0,3x(x+13)-2x(0,9-0,2x)=0
A) 0;4,5 B) 0;-3 C) 0;25/3 D) 0;-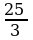 E) 0;-13
E) 0;-13
Теңдемени чыгаргыла : (x – 5 )2 – x2=3
A) x = 2,2 B) x= – 2,2 C) 2,5 D) –2,5 E) x=1,5
Теңдемени чыгаргыла : 2x3+8x = x2+4
A) x = 5 B) x = -5 C) x= - 0,5 D) x = 1/5 E) 3
Теңдемени чыгаргыла : 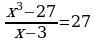
A) –6 B) 6 C) 10 D) 11 E) 9
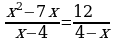 теңдемесин чыгаргыла :
теңдемесин чыгаргыла :
A) –3; -4 B) 3;4 C) –3;4 D) 3 E) –2; -6
Чыгаруу:
Бул теңдемени чыгаруудан мурда теңдеменин жашоо областын аныктап алалы. Мында х – 4 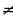 0 жана 4 – х
0 жана 4 – х 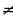 0 болуусу шарт, демек х
0 болуусу шарт, демек х 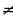 4 болуусу керек. Бул шартты эске алсак (В) жана (С) жооптрун текшерүүнүн зарылчылыгы жок. Теңдемени жөнөкөйлөтөлү
4 болуусу керек. Бул шартты эске алсак (В) жана (С) жооптрун текшерүүнүн зарылчылыгы жок. Теңдемени жөнөкөйлөтөлү 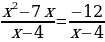 бул барабардыктын бөлүмдөрү бар-абар болгондуктан алымдары да барабар болуусу шарт. Демек
бул барабардыктын бөлүмдөрү бар-абар болгондуктан алымдары да барабар болуусу шарт. Демек
х2 – 7х +12 = 0 теңдемесине ээ болобуз. Теңдемени чыгарсак 3; 4 деген эки тамырга ээ болобуз, экинчи тамыр шартка жооп бербе-гендиктен жообу ( D) болот. Биз адашып (В) деп алышыбыз мүмкүн эгерде теңдеменин жашоо областын текшерип албаганда.
Теңдемени чыгаргыла : 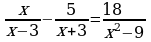
A) –1;3 B) –1; -3 C) –1 D) 3 E) –5; 3
Теңдемени чыгаргыла : 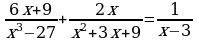
A) 0; -3 B) –3 C) 0 D) 0;3 E) 3;-3
Теңдемени чыгаргыла : 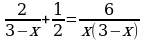
A) 1 B) 2 C) 3 D) 4 E) 5
Теңдемени чыгаргыла : 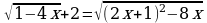
A) –1 B) –2 C) 3 D) –3 E) 2
Теңдемени чыгаргыла : (x+1)(x2+2)+(x+2)(x2+1)=2
A) 1 B) 2 C) –2 D) –1 E) 0
Теңдемени чыгаргыла : 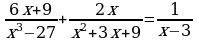
A) 0; -3 B) –3 C) 0 D) 0;3 E) 3;-3
Теңдемени чыгаргыла : 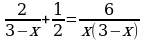
A) 1 B) 2 C) 3 D) 4 E) 5
Теңдемени чыгаргыла : 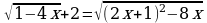
A) –1 B) –2 C) 3 D) –3 E) 2
Теңдемени чыгаргыла : (x+1)(x2+2)+(x+2)(x2+1)=2
A) 1 B) 2 C) –2 D) –1 E) 0
Теңдемени чыгаргыла : 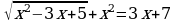
A) 1; -4 B) 4; -1 C) 8; -2 D) 1; 4 E) 3; 5
Теңдемени чыгаргыла : 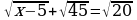
A) чыгарылышы жок B) 10 C) 30 D) 40 E) 30
Эгерде 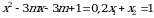 болсо ,m ди тапкыла?
болсо ,m ди тапкыла?
А) 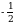 Б)
Б) 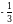 В) 0 Г)
В) 0 Г) 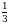 Д)
Д) 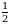
Эгерде 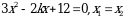 болсо, k ны тапкыла ?
болсо, k ны тапкыла ?
А) 4 Б) 5 В) 6 Г) 7 Д) 8
Эгерде 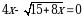 болсо, х ти тапкыла ?
болсо, х ти тапкыла ?
А) 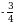 Б)
Б) 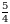 В)
В) 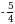 Г)
Г) 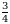 Д)
Д) 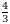
Эгерде 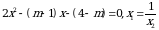 болсо, m ди тапкыла? А)
болсо, m ди тапкыла? А) 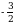 Б) -1 В) 2 Г) 4 Д) 6
Б) -1 В) 2 Г) 4 Д) 6
Эгерде 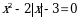 болсо
болсо 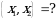 ни тапкыла?
ни тапкыла?
А){-3,3} Б){-3,1} В) {-1,3} Г) {-1,1} Д) {1,3}
Эгерде 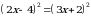 болсо,
болсо, 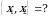 ни тапкыла?
ни тапкыла?
А) 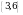 Б)
Б) 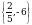 В)
В) 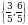 Г)
Г) 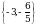 Д)
Д) 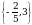
Эгерде 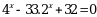 болсо,
болсо,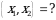 ни тапкыла?
ни тапкыла?
А) { 2 } Б) {0,5} В) {0,2} Г) {1,5} Д) { 0 }
Эгерде 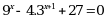 болсо, х ти тапкыла ?
болсо, х ти тапкыла ?
А) {1,2} Б) {3,9} В) {2,4} Г) {0,1} Д) {0,3}
Эгерде 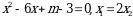 болсо, x ти тапкыла ?
болсо, x ти тапкыла ?
А) 6 Б) 7 В) 8 Г) 10 Д) 11
Эгерде 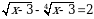 болсо, х ти тапкыла ?
болсо, х ти тапкыла ?
А)15 Б) 17 В) 18 Г)19 Д) 23
Эгерде 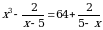 болсо, х ти тапкыла ?
болсо, х ти тапкыла ?
А) -4 Б) -2 В) 3 Г) 4 Д) 8
Эгерде 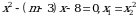 болсо, m ди тапкыла?
болсо, m ди тапкыла?
А) 2 Б) 3 В) 4 Г) 5 Д) 7
Эгерде 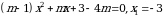 болсо,
болсо, 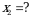 ти
ти
тапкыла ? А) 8 Б) 3 В) 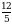 Г)
Г) 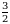 Д)
Д) 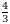
Эгерде 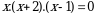 болсо, х = ? ти тапкыла ?
болсо, х = ? ти тапкыла ?
А){0,1,2} Б){0,5} В) {-1,0,2} Г) {1,2} Д) {-2,0,1}
Эгерде 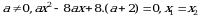 болсо, a ны тапкыла ? А)
болсо, a ны тапкыла ? А) 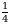 Б)
Б) 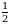 В) 3 Г) 2 Д) 1
В) 3 Г) 2 Д) 1
Эгерде 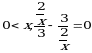 болсо, x ти тапкыла ?
болсо, x ти тапкыла ?
А) 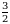 Б)
Б) 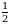 В)
В) 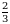 Г)
Г) 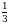 Д) 1
Д) 1
Эгерде 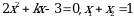 болсо, k ны тапкыла ?
болсо, k ны тапкыла ?
А) 3 Б) 2 В) 1 Г) -1 Д) -2
Эгерде 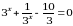 болсо,
болсо, 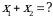 ни тапкыла?
ни тапкыла?
А) -2 Б) -1 В) 0 Г) 1 Д) 2
Эгерде 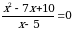 болсо, х ти тапкыла ?
болсо, х ти тапкыла ?
А) {2,5} Б) {5,3} В){2} Г) 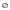 Д) R
Д) R
Үй тапшырма
x2-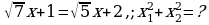
A) 14+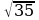 , B) 10+2
, B) 10+2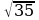 , C) 14+
, C) 14+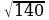 , D)
, D) 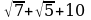 , E) 14+
, E) 14+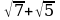
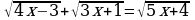 теңдемесин чыгар.
теңдемесин чыгар.
A) 1; -1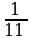 B) –1; 1
B) –1; 1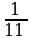 C) 1 D) 1
C) 1 D) 1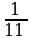 E) -
E) -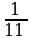
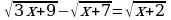 теңдемесин чыгар.
теңдемесин чыгар.
A) 2 B) –2 C) 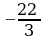 D) 2; -
D) 2; -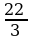 E) –2;
E) –2; 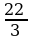
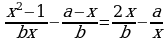 , теңдемесин чыгар.
, теңдемесин чыгар.
A) 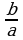 B) b+a C) ab D) b-1 E)
B) b+a C) ab D) b-1 E) 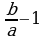
0,05x-0,07(100+x)=40, теңдемесин чыгар.
A) 2300 B) 465 C) 1255 D) 275 E) 250
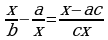 , теңдемесин чыгар. A) a B) b C)
, теңдемесин чыгар. A) a B) b C) 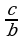 D) c E)
D) c E) 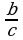
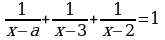 , х = 5 болгондо, a = ?
, х = 5 болгондо, a = ?
A) –2 B) –1 C) 0 D) 1 E) 2
4x2-2xy+y-1=0 y ти x аркылуу туюнт? 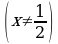
A) y=x B) y=x2 C) y=2x D) y=2x+1 E) y=2x-1
(x-3)2+(3y+48)2 = 0 теңдемесинен, x+y = ?
A) –15 B) 14 C) –13 D) 14 E) 15
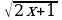 =x-1 теңдемесин чыгар.
=x-1 теңдемесин чыгар.
A) {0} B) {4} C) {0,4} D) {2,0} E) {2}
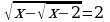 теңдемесин чыгар.
теңдемесин чыгар.
A) {2,1} B) {3,6} C) {1,3} D) {3,4} E) {6}
2tx2-5x+2=0 теңдемесинде х = –1 болсо, t=?
A) 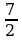 B)
B) 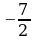 C)
C) 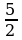 D) -
D) -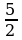 E) 1
E) 1
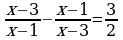 теңдемени чыгар.
теңдемени чыгар.
A)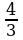 , B)
, B)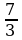 , C) -
, C) -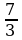 , D) –1, E) 1
, D) –1, E) 1
а нын кандай маанисинде 25х2-25х+12а=0 теңдемеси эки башка чыныгы тамырларга ээ болот ?
A) a 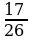 B) a
B) a 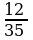 C) a
C) a 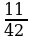 D) a
D) a 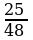 E) a
E) a 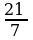
x2+kx-8=0 теңдемеси, x2=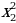 шартын канаатандыруучу x1, x2 жана k нын бүтүн маанисин тап ?
шартын канаатандыруучу x1, x2 жана k нын бүтүн маанисин тап ?
A) –2 B) –1 C) 0 D) 1 E) 2
Эгерде x2+(2m-1)x+m-3= 0(x1 жана x2 теңдеменин тамырлары болсо) x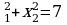 , m = ?
, m = ?
A) {3,4} B) {0,3} C) {0,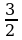 } D) {-1;2} C) {-1,1}
} D) {-1;2} C) {-1,1}
3-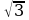 , 3+
, 3+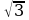 төмөнкү теңдемелердин кимисинин тамырлары болот?
төмөнкү теңдемелердин кимисинин тамырлары болот?
A) x2-x-6=0 B) x2-6x-6=0 C) x2+6x+6=0 D) x2-6x+6=0 E) x2-3=0
x2-2x+a = 0 теңдемеси x1 жана x2 тамырларына ээ болуп
x1+x2+x1 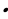 x2 =5 болсо, a ны тап?
x2 =5 болсо, a ны тап?
A) 1 B) 2 C) 3 D) 4 E) 5
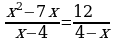 теңдемесин чыгар.
теңдемесин чыгар.
A) –3; -4 B) 3;4 C) –3;4 D) 3; -4 E) –2; -6
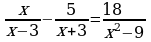 теңдемесин чыгар.
теңдемесин чыгар.
A) –1;3 B) –1; -3 C) –1 D) 3 E) –5; 3
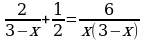 теңдемесин чыгар.
теңдемесин чыгар.
1, B) 2, C) 3, D) 4, E) 5








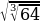
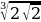
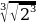
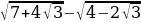
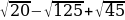
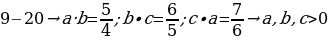
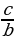
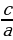
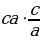
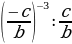
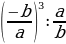
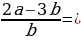 7 а + b сумма-сынын эң чоң маанисин тап ?
7 а + b сумма-сынын эң чоң маанисин тап ? b=30 жана b
b=30 жана b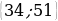 жана ЭКЖБ
жана ЭКЖБ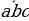 – саны 9 га бөлүнсө жана бирдиги 3 кө барабар болсо, цифралары (a
– саны 9 га бөлүнсө жана бирдиги 3 кө барабар болсо, цифралары (a b
b 7. 95
7. 95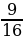 – 88
– 88 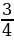 +
+ 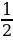
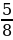 B) 365
B) 365 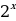 = n жана
= n жана 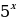 = m болсо, төмөнкүлөрдүн кимиси туура ?
= m болсо, төмөнкүлөрдүн кимиси туура ?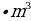 B)
B) 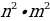 C)
C) 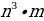 D)
D) 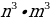 E)
E) 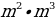
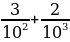 = ?
= ?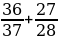 жана b =
жана b = 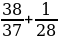 болсо, а ны b аркылуу туюнт.
болсо, а ны b аркылуу туюнт.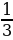 )
)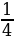 )
)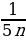 )=63
)=63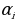 ) = g(
) = g(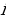 = 1,2,3, ...,п,... )
= 1,2,3, ...,п,... )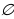 көптүк болот.
көптүк болот.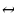 f(x) - g(x) = 0
f(x) - g(x) = 0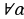 : f(x) = g(x)
: f(x) = g(x)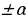 = g(x)
= g(x)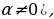 f(x) = g(x)
f(x) = g(x) 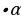 = g(x)
= g(x)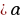 = g(x)
= g(x)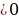 жана а
жана а 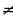 1:
1: 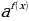 =
= 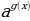
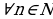 : y = f(x) жана y = g(x) функциялары терс болбосо,
: y = f(x) жана y = g(x) функциялары терс болбосо,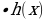 = g(x)
= g(x)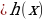 = g(x)
= g(x)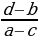 тамырына ээ болобуз ( мында а – с
тамырына ээ болобуз ( мында а – с 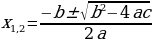 тамырларына;
тамырларына;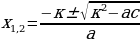 тамырларына;
тамырларына;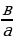 тамырларына ;
тамырларына ;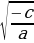 тамырларына ээ болот,
тамырларына ээ болот,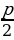 ±
±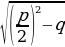 тамырларына ээ болушат. Мындан жогорку даражалуу теңдемелер бош мүчөсүнүн жөнөкөй көбөйүүчүлөрүнө жараша тамырларга ээ болот.
тамырларына ээ болушат. Мындан жогорку даражалуу теңдемелер бош мүчөсүнүн жөнөкөй көбөйүүчүлөрүнө жараша тамырларга ээ болот.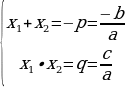 (Виеттин теормасы).
(Виеттин теормасы).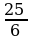 B)
B) 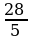 C)
C) 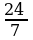 D) 3 E) 2
D) 3 E) 2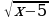 = 5
= 5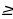 0 болуусу шарт, демек х
0 болуусу шарт, демек х 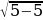 = 5
= 5 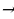 5 + 3
5 + 3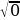 = 5
= 5 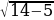 = 5
= 5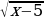 = 5 – х барабардыктын эки жагын тең квадратка көтөрсөк
= 5 – х барабардыктын эки жагын тең квадратка көтөрсөк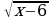 = 6
= 6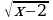 = 7 – 2x
= 7 – 2x 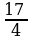 C) 1 D) -3 E) 3;
C) 1 D) -3 E) 3;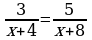
 B)
B) 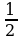 C)
C) 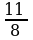 D) 2 E) 4
D) 2 E) 4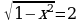
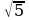 D) чыгарылышы жок
D) чыгарылышы жок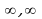 ) D) (3,
) D) (3,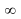 ) E) (-3,
) E) (-3,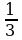 C) чыг.жок D) x1=-1; x2=2, E) x1=2, x2 = -
C) чыг.жок D) x1=-1; x2=2, E) x1=2, x2 = -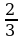
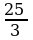 E) 0;-13
E) 0;-13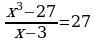
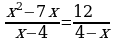 теңдемесин чыгаргыла :
теңдемесин чыгаргыла :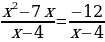 бул барабардыктын бөлүмдөрү бар-абар болгондуктан алымдары да барабар болуусу шарт. Демек
бул барабардыктын бөлүмдөрү бар-абар болгондуктан алымдары да барабар болуусу шарт. Демек 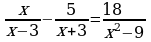
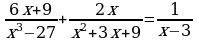
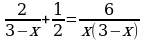
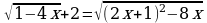
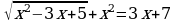
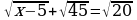
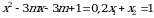 болсо ,m ди тапкыла?
болсо ,m ди тапкыла?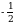 Б)
Б) 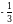 В) 0 Г)
В) 0 Г) 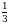 Д)
Д) 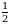
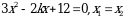 болсо, k ны тапкыла ?
болсо, k ны тапкыла ?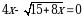 болсо, х ти тапкыла ?
болсо, х ти тапкыла ?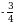 Б)
Б) 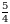 В)
В) 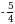 Г)
Г) 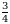 Д)
Д) 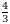
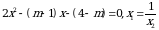 болсо, m ди тапкыла? А)
болсо, m ди тапкыла? А) 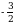 Б) -1 В) 2 Г) 4 Д) 6
Б) -1 В) 2 Г) 4 Д) 6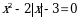 болсо
болсо 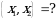 ни тапкыла?
ни тапкыла?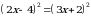 болсо,
болсо, 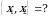 ни тапкыла?
ни тапкыла?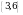 Б)
Б) 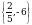 В)
В) 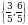 Г)
Г) 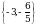 Д)
Д) 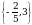
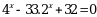 болсо,
болсо,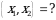 ни тапкыла?
ни тапкыла?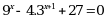 болсо, х ти тапкыла ?
болсо, х ти тапкыла ?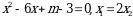 болсо, x ти тапкыла ?
болсо, x ти тапкыла ?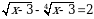 болсо, х ти тапкыла ?
болсо, х ти тапкыла ?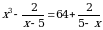 болсо, х ти тапкыла ?
болсо, х ти тапкыла ?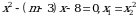 болсо, m ди тапкыла?
болсо, m ди тапкыла?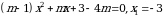 болсо,
болсо, 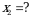 ти
ти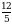 Г)
Г) 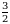 Д)
Д) 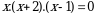 болсо, х = ? ти тапкыла ?
болсо, х = ? ти тапкыла ?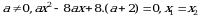 болсо, a ны тапкыла ? А)
болсо, a ны тапкыла ? А) 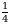 Б)
Б) 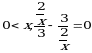 болсо, x ти тапкыла ?
болсо, x ти тапкыла ?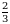 Г)
Г) 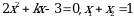 болсо, k ны тапкыла ?
болсо, k ны тапкыла ?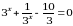 болсо,
болсо, 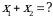 ни тапкыла?
ни тапкыла?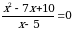 болсо, х ти тапкыла ?
болсо, х ти тапкыла ?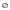 Д) R
Д) R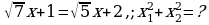
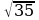 , B) 10+2
, B) 10+2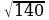 , D)
, D) 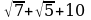 , E) 14+
, E) 14+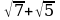
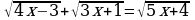 теңдемесин чыгар.
теңдемесин чыгар.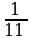 B) –1; 1
B) –1; 1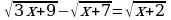 теңдемесин чыгар.
теңдемесин чыгар.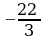 D) 2; -
D) 2; -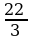 E) –2;
E) –2; 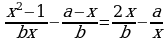 , теңдемесин чыгар.
, теңдемесин чыгар.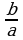 B) b+a C) ab D) b-1 E)
B) b+a C) ab D) b-1 E) 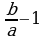
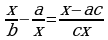 , теңдемесин чыгар. A) a B) b C)
, теңдемесин чыгар. A) a B) b C) 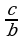 D) c E)
D) c E) 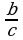
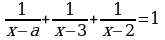 , х = 5 болгондо, a = ?
, х = 5 болгондо, a = ?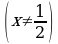
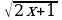 =x-1 теңдемесин чыгар.
=x-1 теңдемесин чыгар.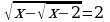 теңдемесин чыгар.
теңдемесин чыгар.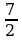 B)
B) 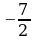 C)
C) 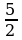 D) -
D) -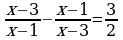 теңдемени чыгар.
теңдемени чыгар. 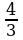 , B)
, B)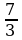 , C) -
, C) -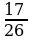 B) a
B) a 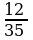 C) a
C) a 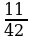 D) a
D) a 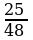 E) a
E) a 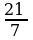
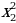 шартын канаатандыруучу x1, x2 жана k нын бүтүн маанисин тап ?
шартын канаатандыруучу x1, x2 жана k нын бүтүн маанисин тап ?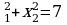 , m = ?
, m = ?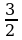 } D) {-1;2} C) {-1,1}
} D) {-1;2} C) {-1,1}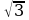 , 3+
, 3+









