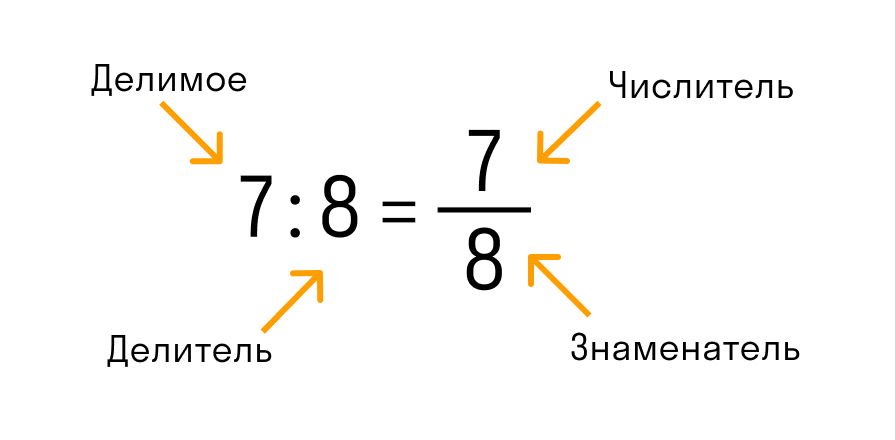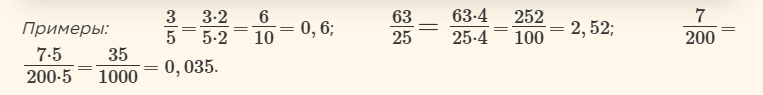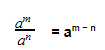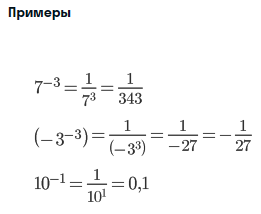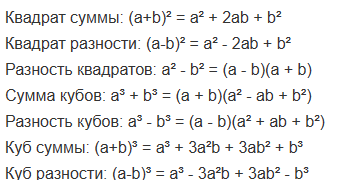Действия над положительными и отрицательными числами, обыкновенными и десятичными дробями

Тема 1.1 Цель и задачи математики при освоении профессии. Числа и вычисления.

Занятие 2: Действия над положительными и отрицательными числами, обыкновенными и десятичными дробями. Действия со степенями, формулы сокращенного умножения

Тип урока: Комбинированный урок.

Цель: заключается в предотвращении забывания усвоенного материала, углублении сведений о ранее изученном, уточнении приобретенных представлений.

Ход урока:

1. Приветствие

2. Актуализация

Что такое положительное\отрицательное число; обыкновенные десятичные дроби; действия с ними; степени; фсу?

1. Объяснение и закрепление повторяемого материала:

Пункт 1: действия над положительными и отрицательными числами

Положительные числа — это числа со знаком «плюс». Они всегда больше нуля. На числовой прямой находятся справа от нуля.

Действия с положительными числами

Вспомним, что с положительными числами возможны любые действия:

• Сложение и вычитание

• Умножение и деление

• Возведение в степень и извлечение корня

• Логарифмирование и т.д.

Отрицательные числа — это числа со знаком минус (−), они всегда меньше нуля. На числовой прямой находятся слева от нуля.

Правила действий с отрицательными и положительными числами

Сложение чисел с одинаковым знаком

• При сложении двух чисел с одинаковым знаком складываются их абсолютные величины и перед суммой ставится общий их знак.

Примеры.
(+8) + (+11) = 19;
(-7) + (-3) = -10.

• При сложении двух чисел с разными знаками из абсолютной величины одного из них вычитается абсолютная величина другого (меньшая из большей) а ставится знак того числа, у которого абсолютная величина больше.

Примеры.
(+7) - (+4) = (+7) + (-4) = 3;
(+7) - (-4) = (+7) + (+4) = 11;
(-7) - (-4) = (-7) + (+4) = -3;
(-4) - (-8) = (-4) + (+8) = 4;

Умножение чисел с разными знаками

При умножении двух чисел умножаются их абсолютные величины и перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные.

Схема (правило знаков при умножении):

Примеры.
( + 2,4) * (-5) = -12; 
(-2,4) * (-5) = 12; 
(-8,2) * (+2) = -16,4.

Примеры.
(-6) : (+3) = -2;
(+8) : (-2) = -4; 
(-12) : (-12) = + 1.

Пункт 2: действия с обыкновенными и десятичными дробями

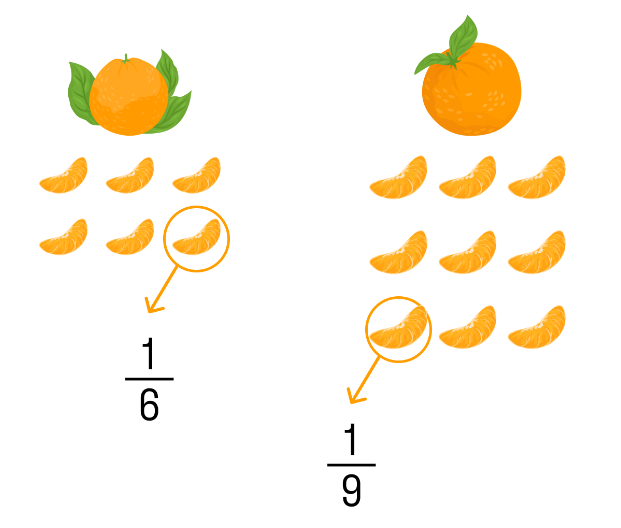
Доля это каждая из равных частей, на которые поделено целое. У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарине шесть долей — каждая из них будет определяться, как одна шестая от целого.

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

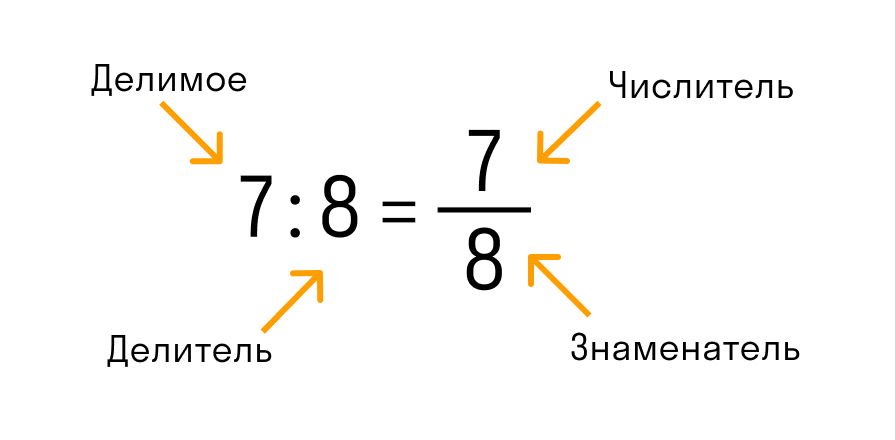
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

С обыкновенными дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой.

Как обыкновенную дробь перевести в десятичную?

Для этого надо домножить числитель и знаменатель дроби на такое число, чтобы в знаменателе получилось 10, 100, 1000 и т.д., а потом записать результат в десятичном виде.

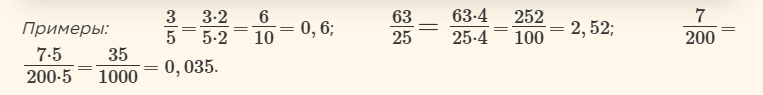
Этот способ хорошо работает, когда в знаменателе дроби: 2, 5, 20, 25… и т.д., то есть когда сразу понятно, на что надо домножать. Однако в остальных случаях:

Для превращения обыкновенной дроби в десятичную нужно поделить числитель дроби на ее знаменатель.

Десятичная дробь — это результат преобразования обыкновенной дроби: деления числителя на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной.

Десятичные дроби можно складывать, вычитать, умножать и делить.

Пункт 3: Действия со степенями

«Степенью n числа а является произведение множителей величиной а n раз подряд»

a^n — степень,

где:

a — основание степени;

n — показатель степени.

Соответственно: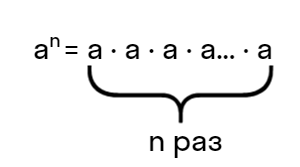

2^3 = 2·2·2, где:

2 — основание степени;

3 — показатель степени.

Свойства степеней:

св-во 1 произведение степеней

При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:

a^n · a^m = a^m+n

a — основание степени

m, n — показатели степени, любые натуральные числа. Натуральные числа - Числа, возникающие естественным образом при счёте

св-во 2 частное степеней

Когда мы делим степени с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.

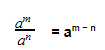
a — любое число, не равное нулю

m, n — любые натуральные числа такие, что m n

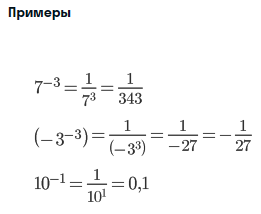
Пункт 4: формулы сокращенного умножения

Формулами сокращенного умножения (ФСУ) называют несколько наиболее часто встречающихся в практике случаев умножения многочленов.

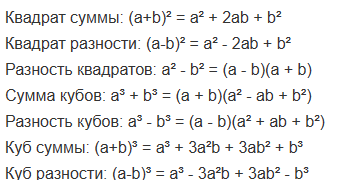
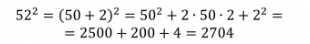
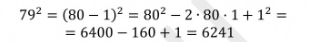
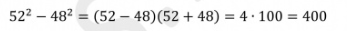
1. Домашнее задание: Проработать конспект.