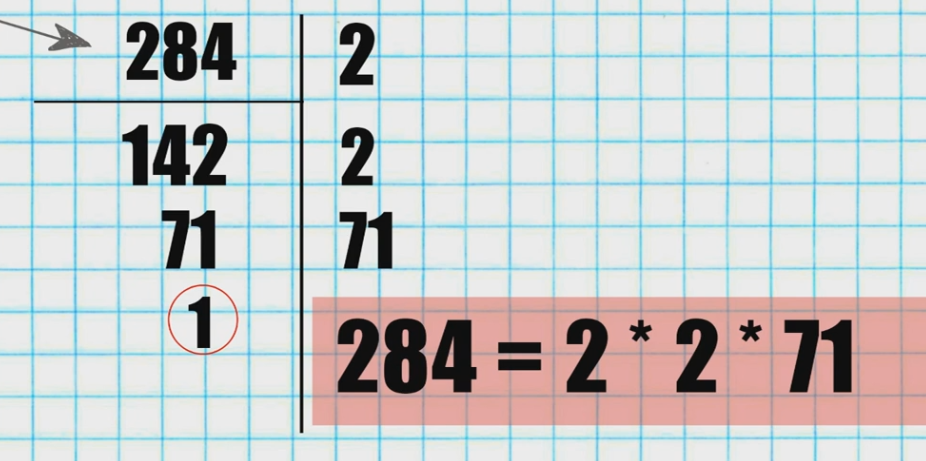Делимость натуральных чисел

Районный конкурс проектных, исследовательских

и творческих работ учащихся.

Образовательная область: естествознание.

Раздел: «Математика»

Исследовательская работа на тему:

«Признаки делимости натуральных чисел »

Автор: Никитина Елизавета,

учащаяся 8 класса

Руководитель:

Цепилова Е. А.

учитель математики.

2014г.

Содержание

1. Введение

2. История делимости натуральных чисел

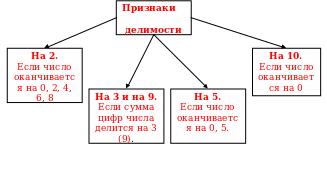
3. Признаки делимости натуральных чисел на 2, на 3, на 9, на 5, на 10, изучаемые в

школьном курсе математики.

4. Признаки делимости на 7, 11, 12, 13, 14, 19, 37, описанные в разных источниках.

5. Признаки делимости натуральных чисел на 4, 6, 8, 15, 25, полученные самостоятельно

6. Применение признаков делимости натуральных чисел при решении задач.

7. Заключение.

1. Введение

Актуальность: При изучении темы: «Признаки делимости натуральных чисел на 2, 3, 5, 9, 10» меня заинтересовал вопрос о делимости чисел. Известно, что не всегда одно натуральное число делится на другое натуральное число без остатка. При делении натуральных чисел, мы допускаем ошибки, в результате - теряем время. Признаки делимости помогают, не выполняя деление установить, делится ли одно натуральное число на другое. На занятиях элективного курса мы рассматривали некоторые другие признаки делимости натуральных чисел. Мне стало интересно, можно ли ещё самой получить новые признаки делимости? Так возникла тема моей исследовательской работы.

Гипотеза: если можно определить делимость натуральных чисел на 2, 3, 5, 9, 10, то должны быть признаки, по которым можно определить делимость натуральных чисел на другие числа.

Объект исследования: делимость натуральных чисел.

Предмет исследования: признаки делимости натуральных чисел.

Цель: дополнить уже известные признаки делимости натуральных чисел нацело, изучаемые в школе.

Задачи:

1. Изучить историю появления признаков делимости.

2. Повторить признаки делимости на 2, 3. 5, 9, 10, изучаемые в школе.

3. Изучить дополнительную литературу, подтверждающую правильность гипотезы о существовании других признаков делимости натуральных чисел и правильность выявленных мной признаков делимости.

4. Получить самостоятельно признаки делимости натуральных чисел на 4, 6, 8, 15, 25.

5. Найти из дополнительной литературы признаки делимости натуральных чисел на 7, 11, 12, 13, 14, 19, 37.

6. Сделать вывод.

Новизна: в ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.

Методы исследования: сбор материала, обработка данных, наблюдение, сравнение, анализ, обобщение.

1. Из истории.

Признак делимости – это правило, по которому, не выполняя деления можно определить, делится ли одно натуральное число на другое. Признаки делимости всегда интересовали ученых разных стран и времен.

Признаки делимости на 2, 3, 5, 9, 10, были известны с давних времен. Признак делимости на 2 знали древние египтяне за 2 тысячи лет до нашей эры, а признаки делимости на 2, 3, 5 были обстоятельно изложены итальянским математиком Леонардо Фибоначчи (1170-1228г.г.).

Вопросы делимости чисел рассматривались пифагорейцами и др.

Блез Паскаль

Большой вклад в изучение признаков делимости чисел внес Блез Паскаль (1623-1662г.г.). Юный Блез очень рано проявил выдающиеся математические способности, научившись считать раньше, чем читать. Свой первый математический трактат «Опыт теории конических сечений» он написал в 24 года. Примерно в это же время он сконструировал механическую суммирующую машинку, прообраз арифмометра. В ранний период своего творчества (1640-1650г.г.) разносторонний ученый нашел алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число, из которого следуют все частные признаки. Его признак состоит в следующем: Натуральное число а разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа a на соответствующие остатки, получаемые при делении разрядных единиц на число b, делится на это число.

1. Признаки делимости натуральных чисел, изучаемые в школе.

При изучении данной темы необходимо знать понятия делитель, кратное, простое и составное числа.

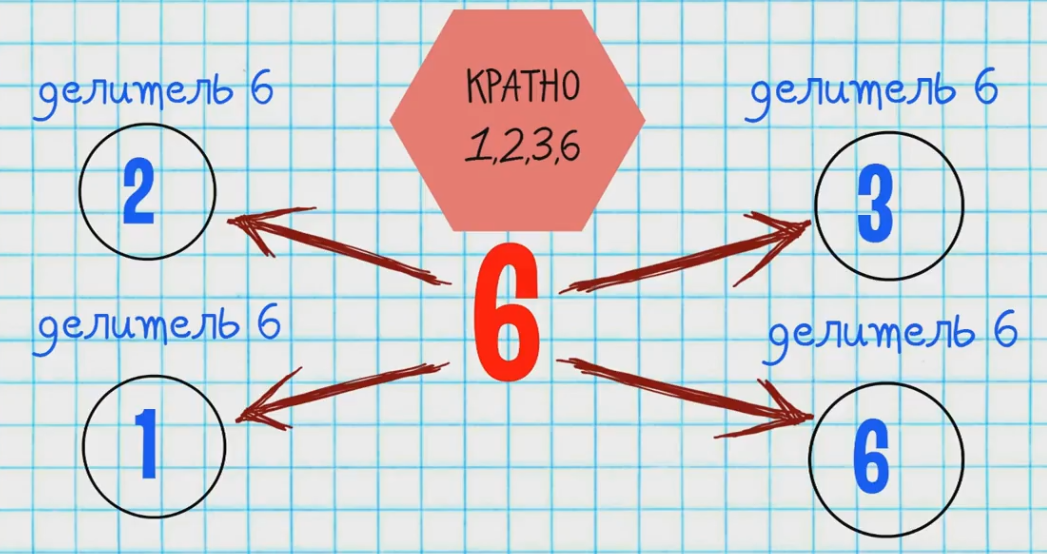
Делителем натурального числа а называют натуральное число b, на которое а делится без остатка.

Часто утверждение о делимости числа а на число b выражают другими равнозначными словами: а кратно b, b - делитель а, b делит а.

Простыми называются натуральные числа, которые имеют два делителя: 1 и само число. Например, числа 5,7,19 – простые, т.к. делятся на 1 и само себя.

Числа, которые имеют более двух делителей, называются составными. Например, число 14 имеет 4 делителя: 1, 2, 7, 14, значит оно составное.

1. Признаки делимости натуральных чисел на 7, 11, 12, 13, 14, 19, 37, описанные в различных источниках.

Из дополнительной литературы я нашла подтверждение правильности сформулированных мной признаков делимости натуральных чисел на 4, 6, 8, 15, 25.

Рассмотрим несколько признаков делимости:

Натуральное число делится на 7, если сумма удвоенного числа, стоящего до десятков и оставшегося числа делится на 7.

Примеры:

4592 делится на 7, т.к. 45·2=90, 90+92=182, 182 делится на 7.

57384 не делится на 7, т.к. 573·2=1146, 1146+84=1230, 1230 не делится на 7.

Число делится на 11, если разность суммы цифр стоящих на нечетных местах, и суммы цифр, стоящих на четных местах кратна 11.

Разность может быть отрицательным числом или 0, но обязательно должна быть кратной 11. Нумерация идет слева направо.

Пример:

2135704 2+3+7+4=16, 1+5+0=6, 16-6=10, 10 не кратно 11, значит, это число не делится на 11.

1352736 1+5+7+6=19, 3+2+3=8, 19-8=11, 11 кратно 11, значит, это число делится на 11.

Натуральное число делится на 12 тогда и только тогда, когда оно делится на 3 и 4 одновременно.

Примеры:

636 делится на 3 и на 4, значит, оно делится на 12.

587 не делится ни на 3, ни на 4, значит, оно не делится на 12.

27126 делится на 3, но не делится на 4, значит, оно не делится на 12.

Натуральное число делится на 13, если разность числа тысяч и числа, образованного последними тремя цифрами, делится на 13.

Примеры:

Число 465400 делится на 13, т.к. 465 – 400 = 65, 65 делится на 13.

Число 256184 не делится на 13, т.к. 256 – 184 = 72, 72 не делится на 13.

Натуральное число делится на 14 тогда и только тогда, когда оно делится на 2 и на 7 одновременно.

Примеры:

Число 45826 делится на 2, но не делится на 7, значит, оно не делится на 14.

Число 1771 делится на 7, но не делится на 2, значит, оно не делится на 14.

Число 35882 делится на 2 и на 7, значит, оно делится на 14.

Натуральное число делится на 19 без остатка тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, делится на 19.

Следует учесть, что число десятков в числе надо считать не цифру в разряде десятков, а общее число целых десятков во всем числе.

Примеры:

1534 десятков-153, 4·2=8, 153+8=161, 161 не делится на 19,значит, и 1534 не делится на 19.

1824 182+4·2=190, 190/19, значит, число 1824/19.

Натуральное число делится на 37, если сумма чисел, образованных тройками цифр данного числа в десятичной записи делится соответственно на 37.

Пример: Определим, делится ли число 100048 на 37.

100/048 100+48=148, 148 делится на 37, значит, и число делится на 37.

1. Признаки делимости натуральных чисел на 4, 6, 8, 15, 25, полученные самостоятельно.

Выполняя действия деления, умножения натуральных чисел, наблюдая за результатами действий, я нашла закономерности и получил следующие признаки делимости.

25·4=100; 56·4=224; 123·4=492; 125·4=500; 2345·4=9380; 2500·4=10000; …

Умножая натуральные числа на 4, я заметил, что числа образованные из двух последних цифр числа делятся на 4 без остатка.

Признак делимости на 4 читается так:

Натуральное число делится на 4 тогда и только тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.

Заметим, что 6=2·3 Признак делимости на 6:

Если натуральное число одновременно делится на 2 и на 3, то оно делится на 6.

Примеры:

216 делится на 2 (оканчивается 6) и делится на 3 (8+1+6=15, 15׃3), значит, число делится на 6.

625 не делится ни на 2, ни на 3, значит, не делится на 6.

2120 делится на 2 (оканчивается 0), но не делится на 3 (2+1+2+0=5, 5 не делится на 3), значит, число не делится на 6.

279 делится на 3 (2+7+9=18, 18:3), но не делится на 2 (оканчивается нечетной цифрой), значит, число не делится на 6.

125·8=1000; 242·8=1936; 512·8=4096; 600·8=4800; 1234·8=9872; 122875·8=983000;…

Умножая натуральное число на 8, я заметила такую закономерность, числа оканчиваются на три 0-ля или три последние цифры составляют число, которое делится на 8.

Значит, признак таков.

Натуральное число делится на 8 тогда и только тогда, когда три его последние цифры 0 или составляют число, делящееся на 8.

Заметим, что 15=3·5

Ели натуральное число одновременно делится и на 5 и на 3, то оно делится на 15.

Примеры:

346725 делится на 5 (оканчивается 5) и делится на 3 (3+4+6+7+2+5=24, 24:3), значит, число делится на 15.

48732 делится на 3 (4+8+7+3+2=24, 24:3), но не делится на 5,значит, число не делится на 15.

87565 делится на 5 (оканчивается 5), но не делится на 3 (8+7+5+6+5=31, 31 не делится на 3),

Выполняя умножение натуральных различных чисел на 25, я увидела такую закономерность: произведения оканчиваются на 00, 25, 50, 75.

Значит, натуральное число делится на 25, если оканчивается на 00, 25, 50, 75.

Все перечисленные признаки делимости натуральных чисел можно разделить на 4 группы:

1группа- когда делимость чисел определяется по последней(им) цифрой (ми)- это признаки делимости на 2, на 5, , на 4, на 8, на 25.

2 группа – когда делимость чисел определяется по сумме цифр числа- это признаки делимости на 3, на 9, на7, на 37.

3 группа – когда делимость чисел определяется после выполнения каких-то действий над цифрами числа- это признаки делимости на 7, на 11, на 13, на 19.

4 группа – когда для определения делимости числа используются другие признаки делимости- это признаки делимости на 6, на 15, на 12, на14.

6. Применение признаков делимости натуральных чисел при решении задач.

Признаки делимости применяются при нахождении НОД и НОК, а также при решении текстовых задач на применении НОД и НОК.

Задача 1: (Использование общих делителей и НОД)

Ученики 6 класса купили 203 учебника. Каждый купил одинаковое количество книг. Сколько было пятиклассников, и сколько учебников купил каждый из них?

Решение: Обе величины, которые требуется определить должны быть целыми числами, т.е. находиться среди делителей числа 203. Разложив 203 на множители, получаем:

203 = 1 ∙ 7 ∙ 29.

Из практических соображений следует, что учебников не может быть 29. также число учебников не может равняться 1, т.к. в этом случае учеников было бы 203. Значит, пятиклассников – 29 и каждый из них купил по 7 учебников.

Ответ: 29 шестиклассников; 7 учебников

Задача 2. Имеется 60 апельсинов, 165 орехов и 225 конфет. Какое наибольшее число одинаковых подарков для детей можно сделать из этого запаса? Что войдёт в каждый набор?

Решение:

Количество подарков должно быть делителем каждого из чисел, выражающих количество апельсинов, конфет и орехов, причем наибольшим из этих чисел. Поэтому надо найти НОД данных чисел. НОД (60, 175, 225) = 15. Каждый подарок будет содержать: 60 : 15 = 4 – апельсина, 175 : 15 = 11 – орехов и 225 : 15 = 15 – конфет.

Ответ: В одном подарке – 4 апельсина, 11 орехов, 15 конфет.

Задача 3: В 9 классе за контрольную работу 1/7 учеников получили пятёрки, 1/3 – четверки, 1/2 - тройки. Остальные работы оказались неудовлетворительными. Сколько было таких работ?

Решение: Решением задачи должно являться число, кратное числам: 7, 3, 2. Найдем сначала наименьшее из таких чисел. НОК (7, 3, 2) = 42. Можно составить выражение по условию задачи: 42 – (42 : 7 + 42 : 3 + 42 : 2) = 1 – 1 неуспевающий.

Математические отношения задачи допускают, что число учеников в классе 84, 126 и т.д. человек. Но из соображений здравого смысла следует, что наиболее приемлемым ответом является число 42.

Ответ: 1 работа.

Задача 4.

В двух классах вместе 70 учеников. В одном классе 7/17 учеников не явились на занятия, а в другом 2/9 получили отличные отметки по математике. Сколько учеников в каждом классе?

Решение: В первом из этих классов могло быть: 17, 34, 51… - числа, кратные 17. Во втором классе: 9, 18, 27, 36, 45, 54… - числа, кратные 9. Нам нужно выбрать 1 число из первой последовательности, а 2 число из второй так, чтобы они в сумме давали 70. Причем в этих последовательностях только небольшое число членов могут выражать возможное кол-во детей в классе. Это соображение существенно ограничивает перебор вариантов. Возможным единственным вариантом оказалась пара (34, 36).

Ответ: В первом классе – 34 ученика, во втором классе – 36 учеников.

Задача 5.

Два автобуса отправляются от одной площади по разным маршрутам. У одного из автобусов рейс туда и обратно длится 48 мин, а у другого 1 ч 12 мин. Через сколько времени автобусы снова встретятся на этой же площади?

Решение: НОК(48, 72) = 144 (мин). 144 мин = 2 ч 24 мин.

Ответ: Через 2 ч 24 мин автобусы снова встретятся на этой же площади.

Задача 6.

Ваня задумал простое трехзначное число, все цифры которого различны. На какую цифру оно может оканчиваться, если его последняя цифра равна сумме первых двух. Приведите примеры таких чисел.

Ответ: Может оканчиваться только на цифру 7. Таких чисел 4: 167, 257, 347, 527.

7. Заключение.

Выводы:

Выполняя работу, я познакомилась с историей развития признаков делимости, сформулировала признаки делимости натуральных чисел на 4, 6, 8, 15, 25, и нашла подтверждение этого из дополнительной литературы. А так же убедилась в том, что существуют другие признаки делимости натуральных чисел (на 7, 11, 12, 13, 14, 19, 37), что подтвердило правильность гипотезы о существовании других признаков делимости натуральных чисел.

Список использованной литературы (источников):

1. Галкин В.А. Задачи по теме «Признаки делимости ».// Математика, 1999.-№5.-С.9.

2. Гусев В.А., Орлов А.И., Розенталь А.Л. Внеклассная работа по математике в 6-8 классах.- М.: Просвещение, 1984.

3. Каплун Л.М. НОД и НОК в задачах. // Математика, 1999.- №7. – С. 4-6.

4. Пельман Я.И. Математика – это интересно ! – М.: ТЕРРА – Книжный клуб, 2006.

5. Энциклопедический словарь юного математика./ Сост. Савин А.П. – М.: Педагогика, 1989. – С. 352.

6. Ресурсы- Internet.