Деревья. Основные понятия. Графы. Основные понятия

37-38 урок, 11 класс – теория

Учитель: Брух Т.В.

Дата:____________

Тема урока: «Деревья. Основные понятия. Графы. Основные понятия»

Цель: Обеспечить в ходе урока усвоение определенных основных понятий, теорем, а также научных фактов.

Развивать память, умение сравнивать, выявлять закономерности.

Воспитание ответственного отношения к своему труду и труду других участников образовательного процесса.

Ход урока

I Орг. момент

II Проверка домашнего задания

III Объяснение нового материала

Введение

Неформально граф можно рассматривать как множество точек и соединяющих эти точки линий со стрелками или без них.

Первой работой теории графов как математической дисциплины считают статью Эйлера (1736 г.), в которой рассматривалась задача о Кёнингсбергских мостах. Эйлер показал, что нельзя обойти семь городских мостов и вернуться в исходную точку, пройдя по каждому мосту ровно один раз. Следующий импульс теория графов получила спустя почти 100 лет с развитием исследований по электрическим сетям, кристаллографии, органической химии и другим наукам.

С графами, сами того не замечая, мы сталкиваемся постоянно. Например, графом является схема линий метрополитена. Точками на ней представлены станции, а линиями — пути движения поездов. Исследуя свою родословную и возводя ее к далекому предку, мы строим так называемое генеалогическое древо. И это древо — граф.

Графы служат удобным средством описания связей между объектами. Ранее мы уже использовали графы как способ наглядного представления конечных бинарных отношений. Но граф используют отнюдь не только как иллюстрацию. Например, рассматривая граф, изображающий сеть дорог между населенными пунктами, можно определить маршрут проезда от пункта А до пункта Б. Если таких маршрутов окажется несколько, хотелось бы выбрать в определенном смысле оптимальный, например самый короткий или самый безопасный. Для решения задачи выбора требуется проводить определенные вычисления над графами. При решении подобных задач удобно использовать алгебраическую технику, да и само понятие графа необходимо формализовать.

Методы теории графов широко применяются в дискретной математике. Без них невозможно обойтись при анализе и синтезе различных дискретных преобразователей: функциональных блоков компьютеров, комплексов программ и т.д.

В настоящее время теория графов охватывает большой материал и активно развивается. При ее изложении ограничимся только частью результатов и основной акцент сделаем на описании и обосновании некоторых широко распространенных алгоритмов анализа графов, которые применяются в теории формальных языков.

Графы, как уже отмечалось в примерах, есть способ "визуализации" связей между определенными объектами. Связи эти могут быть "направленными", как, например, в генеалогическом древе, или "ненаправленными" (сеть дорог с двусторонним движением). В соответствии с этим в теории графов выделяют два основных типа графов: ориентированные (или направленные) и неориентированные.

Построение математического определения графа осуществляется путем формализации и "объектов", и "связей" как элементов некоторых (как правило, конечных) множеств.

Основные понятия и определения

Опр. ГРАФОМ - НАЗЫВАЕТСЯ ПАРА ДВУХ КОНЕЧНЫХ МНОЖЕСТВ: МНОЖЕСТВО ТОЧЕК И МНОЖЕСТВО ЛИНИЙ, СОЕДИНЯЮЩИХ НЕКОТОРЫЕ ПАРЫ ТОЧЕК.

Опр. ТОЧКИ НАЗЫВАЮТСЯ ВЕРШИНАМИ, ИЛИ УЗЛАМИ, ГРАФА, ЛИНИИ – РЕБРАМИ ГРАФА.

Опр. ЕСЛИ РЕБРО ГРАФА СОЕДИНЯЕТ ДВЕ ЕГО ВЕРШИНЫ, ТО ГОВОРЯТ, ЧТО ЭТО РЕБРО ИМ ИНЦИДЕНТНО. ДВЕ ВЕРШИНЫ ГРАФА НАЗЫВАЮТСЯ СМЕЖНЫМИ, ЕСЛИ СУЩЕСТВУЕТ ИНЦИДЕНТНОЕ ИМ РЕБРО.

Опр. ЕСЛИ РЕБРО ГРАФА СОЕДИНЯЕТ ДВЕ ЕГО ВЕРШИНЫ, ТО ГОВОРЯТ, ЧТО ЭТО РЕБРО ИМ ИНЦИДЕНТНО. ДВЕ ВЕРШИНЫ ГРАФА НАЗЫВАЮТСЯ СМЕЖНЫМИ, ЕСЛИ СУЩЕСТВУЕТ ИНЦИДЕНТНОЕ ИМ РЕБРО.

Опр. ЕСЛИ ГРАФ ИМЕЕТ РЕБРО, У КОТОРОГО НАЧАЛО И КОНЕЦ СОВПАДАЮТ, ТО ЭТО РЕБРО НАЗЫВАЕТСЯ ПЕТЛЕЙ (у графа петля – q(C,C)).

Опр. ДВА РЕБРА НАЗЫВАЮТСЯ СМЕЖНЫМИ, ЕСЛИ ОНИ ИМЕЮТ ОБЩУЮ ВЕРШИНУ.

Опр. ЧИСЛО РЕБЕР, ИНЦИДЕНТНЫХ ВЕРШИНЕ A , НАЗЫВАЕТСЯ СТЕПЕНЬЮ ЭТОЙ ВЕРШИНЫ И ОБОЗНАЧАЕТСЯ deg(A).

ЕСЛИ ВЕРШИНЕ ИНЦИДЕНТНА ПЕТЛЯ, ОНА ДАЕТ ВКЛАД В СТЕПЕНЬ, РАВНЫЙ ДВУМ, ТАК КАК ОБА КОНЦА ПРИХОДЯТ В ЭТУ ВЕРШИНУ.

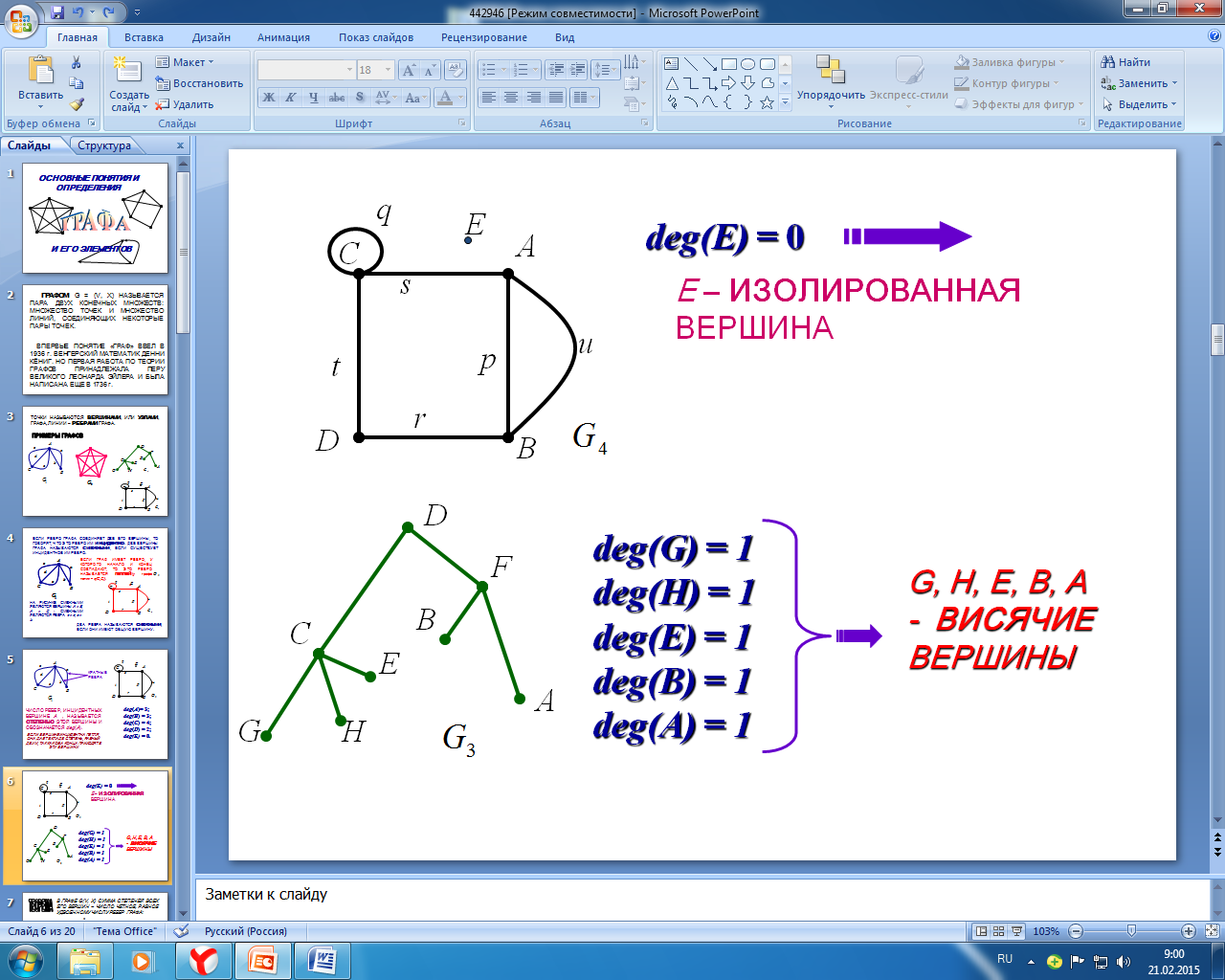
Теорема: В ГРАФЕ G(V, X) СУММА СТЕПЕНЕЙ ВСЕХ ЕГО ВЕРШИН – ЧИСЛО ЧЕТНОЕ, РАВНОЕ УДВОЕННОМУ ЧИСЛУ РЕБЕР ГРАФА:

Теорема: ЧИСЛО НЕЧЕТНЫХ ВЕРШИН ЛЮБОГО ГРАФА – ЧЕТНО.

Следствие: НЕВОЗМОЖНО НАЧЕРТИТЬ ГРАФ С НЕЧЕТНЫМ ЧИСЛОМ НЕЧЕТНЫХ ВЕРШИН.

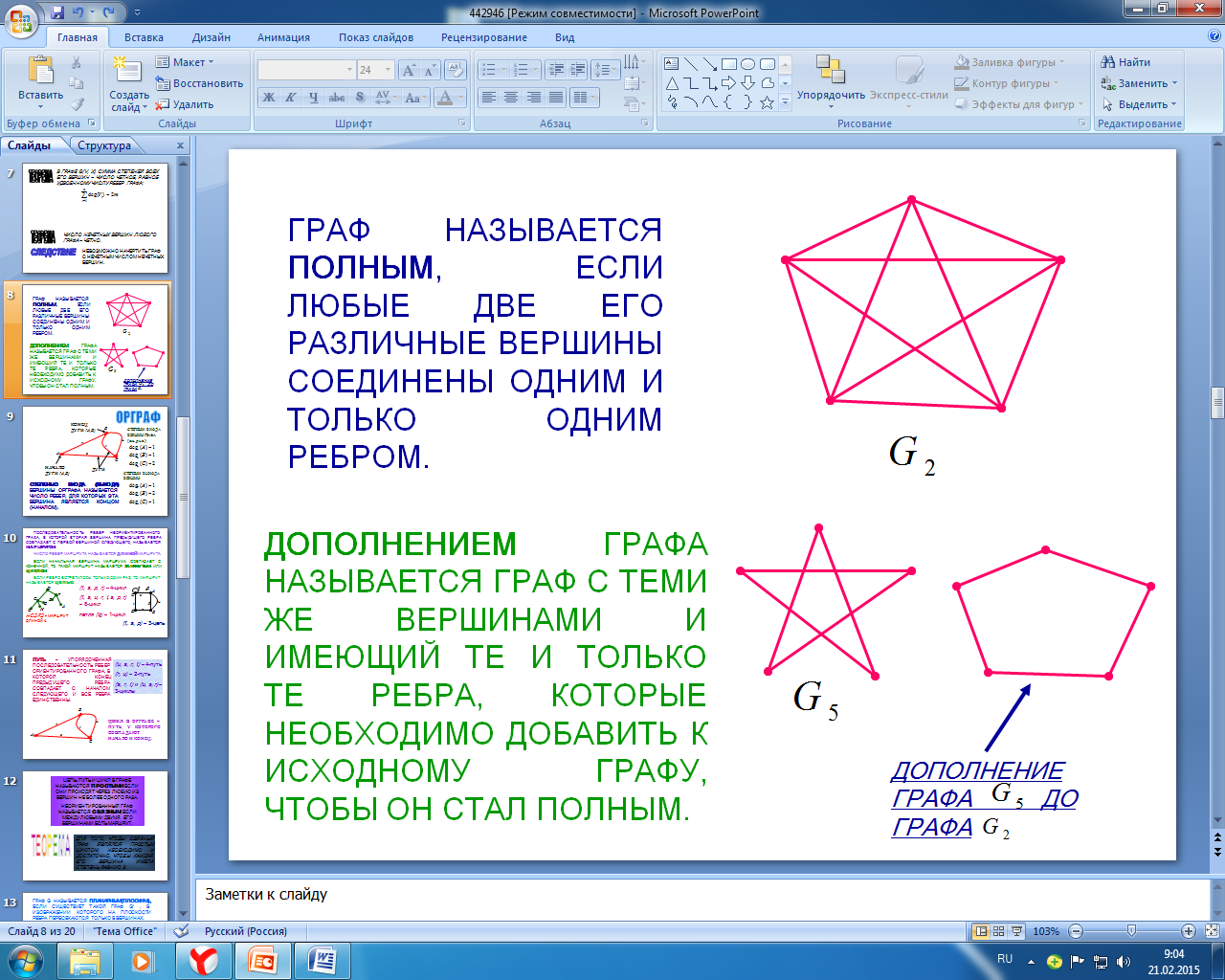
Опр. ГРАФ НАЗЫВАЕТСЯ ПОЛНЫМ, ЕСЛИ ЛЮБЫЕ ДВЕ ЕГО РАЗЛИЧНЫЕ ВЕРШИНЫ СОЕДИНЕНЫ ОДНИМ И ТОЛЬКО ОДНИМ РЕБРОМ.

Опр. ДОПОЛНЕНИЕМ ГРАФА НАЗЫВАЕТСЯ ГРАФ С ТЕМИ ЖЕ ВЕРШИНАМИ И ИМЕЮЩИЙ ТЕ И ТОЛЬКО ТЕ РЕБРА, КОТОРЫЕ НЕОБХОДИМО ДОБАВИТЬ К ИСХОДНОМУ ГРАФУ, ЧТОБЫ ОН СТАЛ ПОЛНЫМ.

Опр. ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР НЕОРИЕНТИРОВАННОГО ГРАФА, В КОТОРОЙ ВТОРАЯ ВЕРШИНА ПРЕДЫДУЩЕГО РЕБРА СОВПАДАЕТ С ПЕРВОЙ ВЕРШИНОЙ СЛЕДУЮЩЕГО, НАЗЫВАЕТСЯ МАРШРУТОМ.

Опр. ЧИСЛО РЕБЕР МАРШРУТА НАЗЫВАЕТСЯ ДЛИНОЙ МАРШРУТА.

ОПР. ЕСЛИ НАЧАЛЬНАЯ ВЕРШИНА МАРШРУИА СОВПАДАЕТ С КОНЕЧНОЙ, ТО ТАКОЙ МАРШРУТ НАЗЫВАЕТСЯ ЗАМКНУТЫМ ИЛИ ЦИКЛОМ.

Опр. ЕСЛИ РЕБРО ВСТРЕТИЛОСЬ ТОЛЬКО ОДИН РАЗ, ТО МАРШРУТ НАЗЫВАЕТСЯ ЦЕПЬЮ.

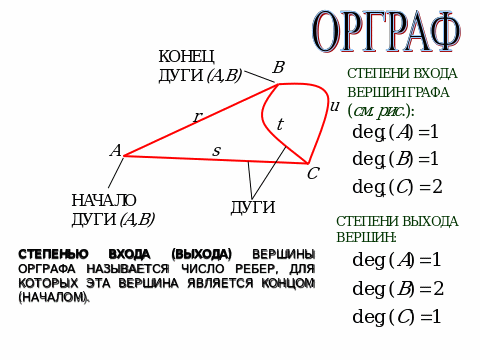
Опр. ПУТЬ – УПОРЯДОЧЕННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР ОРИЕНТИРОВАННОГО ГРАФА, В КОТОРОЙ КОНЕЦ ПРЕДЫДУЩЕГО РЕБРА СОВПАДАЕТ С НАЧАЛОМ СЛЕДУЮЩЕГО И ВСЕ РЕБРА ЕДИНСТВЕННЫ.

(u, s, r, t) – 4-путь

(r, u) – 2-путь

(s, r, t) и (u, s, r) – 3-циклы

Опр. ЦИКЛ В ОРГРАФЕ – ПУТЬ, У КОТОРОГО СОВПАДАЮТ НАЧАЛО И КОНЕЦ.

Опр. ЦЕПЬ, ПУТЬ И ЦИКЛ В ГРАФЕ НАЗЫВАЮТСЯ ПРОСТЫМИ, ЕСЛИ ОНИ ПРОХОДЯТ ЧЕРЕЗ ЛЮБУЮ ИЗ ВЕРШИН НЕ БОЛЕЕ ОДНОГО РАЗА.

Опр. НЕОРИЕНТИРОВАННЫЙ ГРАФ НАЗЫВАЕТСЯ СВЯЗНЫМ, ЕСЛИ МЕЖДУ ЛЮБЫМИ ДВУМЯ ЕГО ВЕРШИНАМИ ЕСТЬ МАРШРУТ.

Теорема: ДЛЯ ТОГО, ЧТОБЫ СВЯЗНЫЙ ГРАФ ЯВЛЯЛСЯ ПРОСТЫМ ЦИКЛОМ, НЕОБХОДИМО И ДОСТАТОЧНО, ЧТОБЫ КАЖДАЯ ЕГО ВЕРШИНА ИМЕЛА СТЕПЕНЬ, РАВНУЮ 2.

Опр. ДЛЯ ТОГО, ЧТОБЫ СВЯЗНЫЙ ГРАФ ЯВЛЯЛСЯ ПРОСТЫМ ЦИКЛОМ, НЕОБХОДИМО И ДОСТАТОЧНО, ЧТОБЫ КАЖДАЯ ЕГО ВЕРШИНА ИМЕЛА СТЕПЕНЬ, РАВНУЮ 2.

Опр. ЭЙЛЕРОВЫМ ПУТЕМ (ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ (ЦИКЛ), КОТОРЫЙ СОДЕРЖИТ ВСЕ РЕБРА ГРАФА ТОЛЬКО ОДИН РАЗ.

Опр. ГРАФ, ОБЛАДАЮЩИЙ ЭЙЛЕРОВЫМ ЦИКЛОМ, НАЗЫВАЕТСЯ ЭЙЛЕРОВЫМ.

Теорема: ГРАФ ЯВЛЯЕТСЯ ЭЙЛЕРОВЫМ ТОГДА И ТОЛЬКО ТОГДА, КОГДА ОН – СВЯЗНЫЙ ГРАФ, ИМЕЮЩИЙ ВСЕ ЧЕТНЫЕ ВЕРШИНЫ.

Опр. ГАМИЛЬТОНОВЫМ ПУТЕМ (ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), ПРОХОДЯЩИЙ ЧЕРЕЗ КАЖДУЮ ЕГО ВЕРШИНУ ТОЛЬКО ОДИН РАЗ.

Опр. ГРАФ, СОДЕРЖАЩИЙ ГАМИЛЬТОНОВ ЦИКЛ, НАЗЫВАЕТСЯ ГАМИЛЬТОНОВЫМ.

Опр. МАТРИЦЕЙ ИНЦИДЕНТНОСТИ ГРАФА G НАЗЫВАЮТ ТАБЛИЦУ B, СОСТОЯЩУЮ ИЗ n СТРОК (ВЕРШИНЫ) И m СТОЛБЦОВ (РЕБРА), В КОТОРОЙ:

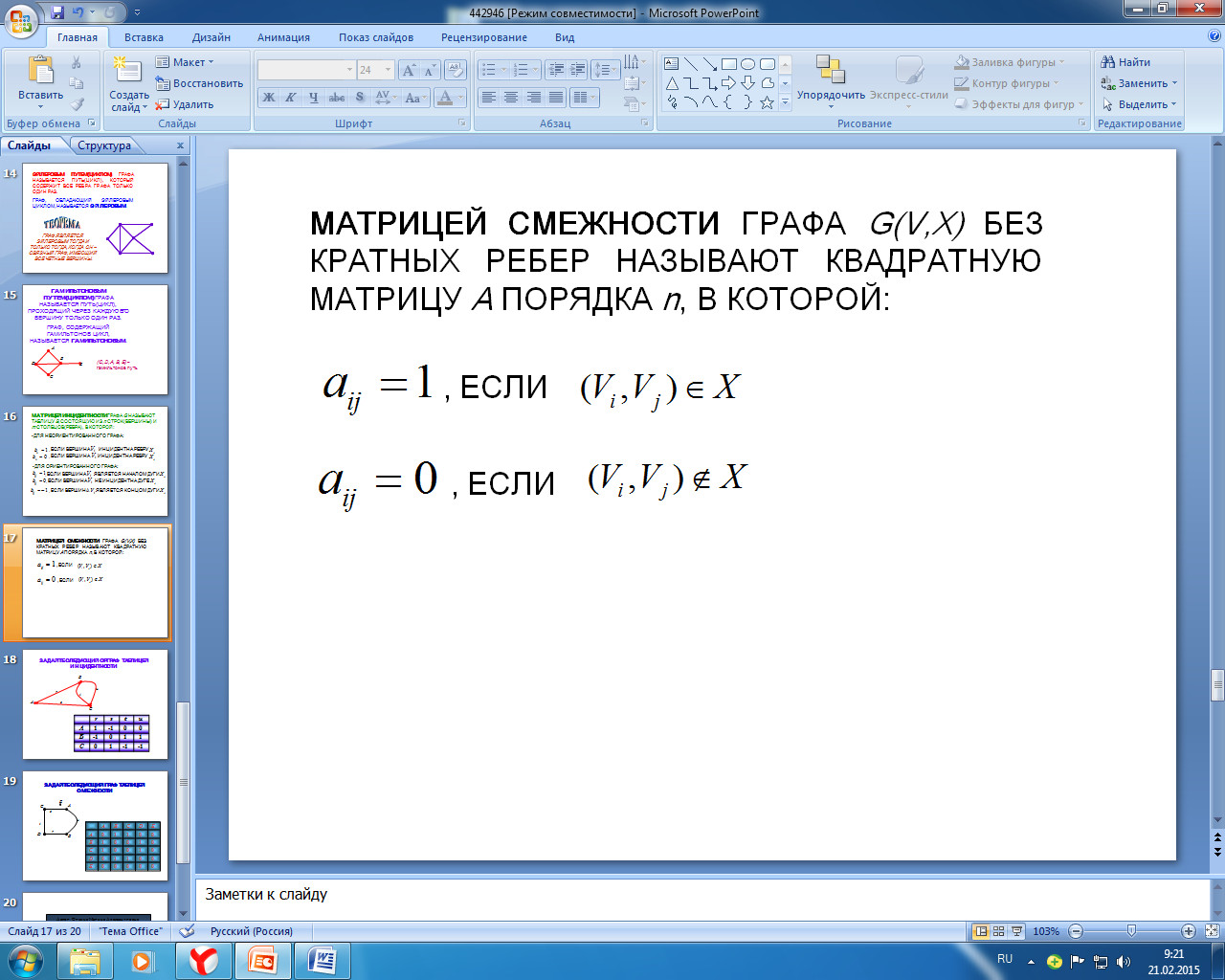
Опр. МАТРИЦЕЙ СМЕЖНОСТИ ГРАФА G(V,X) БЕЗ КРАТНЫХ РЕБЕР НАЗЫВАЮТ КВАДРАТНУЮ МАТРИЦУ A ПОРЯДКА n, В КОТОРОЙ:

Д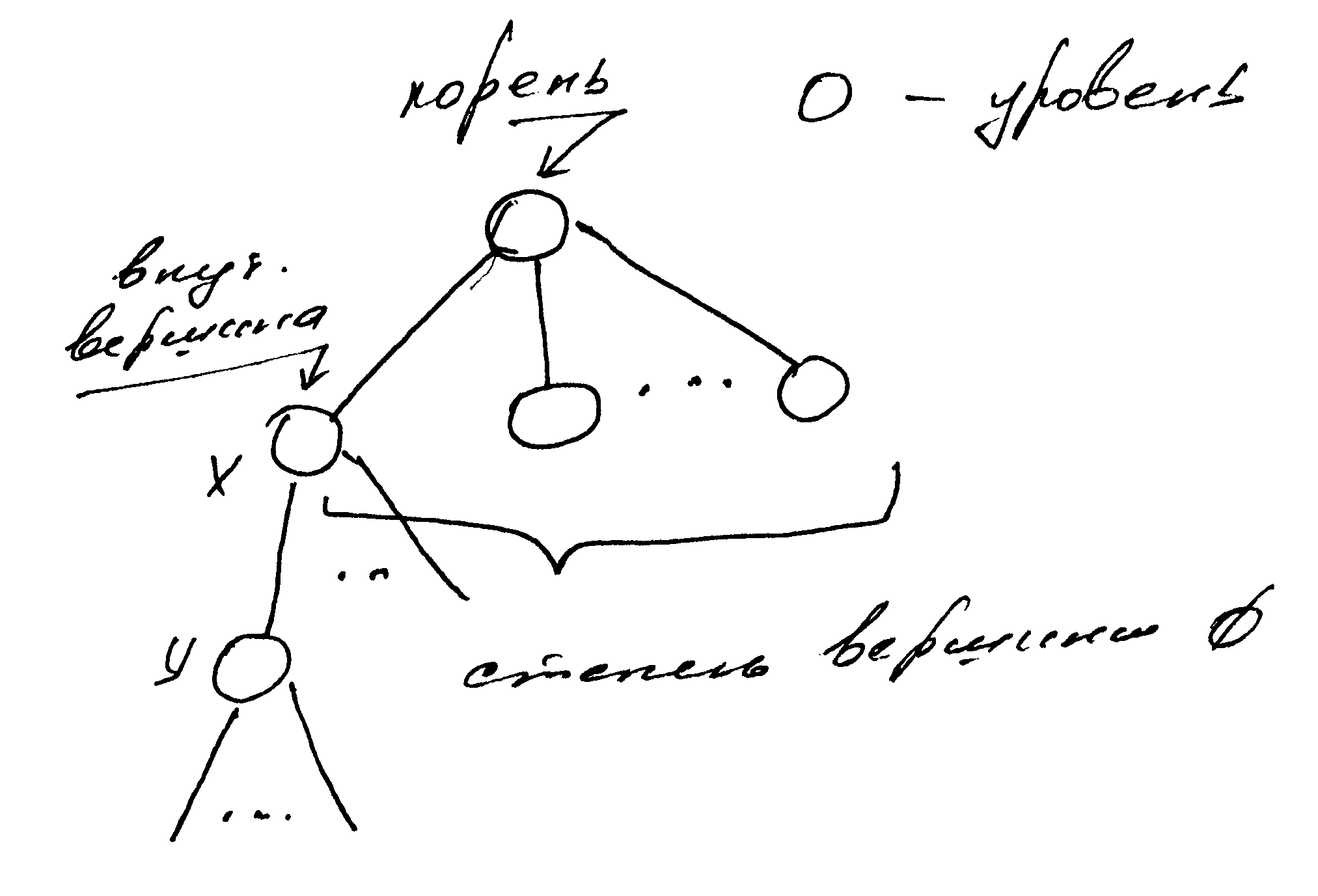 еревья. Основные понятия и определения.

Максимальный уровень вершин дерева называется его глубиной.

Максимальная степень всех вершин есть степень дерева.

Упорядоченное дерево– у которого ребра исходящие из каждой вершины упорядочены.

Двоичные деревья – это упорядоченные деревья второй степени.

Упорядоченное двоичное дерево– это конечное множество вершин (элементов), которое либо пусто, либо состоит из корня (вершины) с двумя отдельными двоичными деревьями, которые называются левыми правым поддеревом этого корня.

IV Закрепление

Вопросы:

1. На рисунке G1 назовите смежные вершины, смежные ребра?

Ответ: НА РИСУНКЕ СМЕЖНЫМИ ЯВЛЯЮТСЯ ВЕРШИНЫ A и B, A и C; СМЕЖНЫМИ ЯВЛЯЮТСЯ РЕБРА c и d, a и b.

1. Найдите степень вершин:

a)

b)

c)

V Домашнее задание: Выучить понятия, определения и теоремы данной темы

VI Итог урока