Движение графиков функций

ГБОУ «Гимназия «Диалог»

• учитель математики Джигкаева Т.З.

Движения графиков функций

y

y=f(x)

Данная презентация может быть использована при проведении уроков в 8-ом классе по теме «Построение графика квадратичной функции с использованием движения графиков», а также для самостоятельного изучения данного материала.

Презентация может быть использована как полностью, так и частично в зависимости от желания преподавателя.

В предлагаемой работе показано пошаговое построение графика функции с использованием некоторых видов движения графиков, что дает возможность учащемуся самостоятельно разобраться с данным материалом.

Также присутствуют задания для самостоятельной работы трех уровней.

Предполагается дальнейшая разработка данной презентации для учащихся старших классов с использованием показательной, логарифмической и тригонометрических функций.

х

o

Рассмотрим некоторые виды движения графиков функций.

Пусть y=f(x) – исходная функция.

f(x) f(x + а )

f(x) f(x) + b

f(x) - f(x)

f(x) f(  x  )

f(x)  f(x) 

Задания для самостоятельной работы

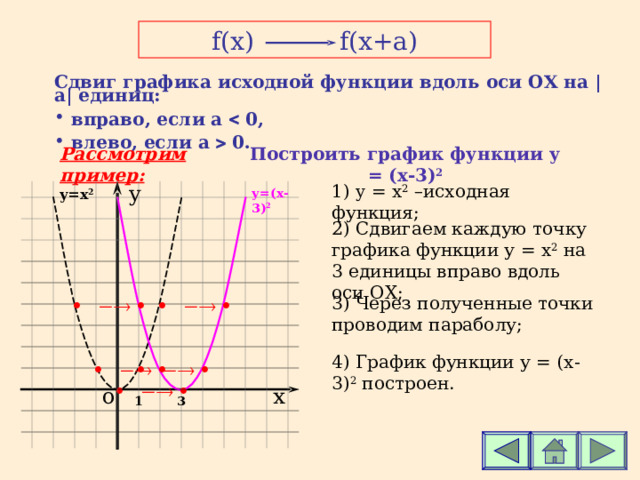
f(x) f(x+a)

Сдвиг графика исходной функции вдоль оси ОХ на | а | единиц:

• вправо, если а  0,
• влево, если а  0.

Рассмотрим пример:

Построить график функции у = ( x- 3 ) 2

y

1) y = x 2 – исходная функция;

y=x 2

у=( x -3) 2

2 ) Сдвигаем каждую точку графика функции у = x 2 на 3 единицы вправо вдоль оси ОХ;

•

• 

• 

•

3 ) Через полученные точки проводим параболу;

4 ) График функции у = ( x -3) 2 построен.

•

•

• 

• 

•

• 

о

х

3

1

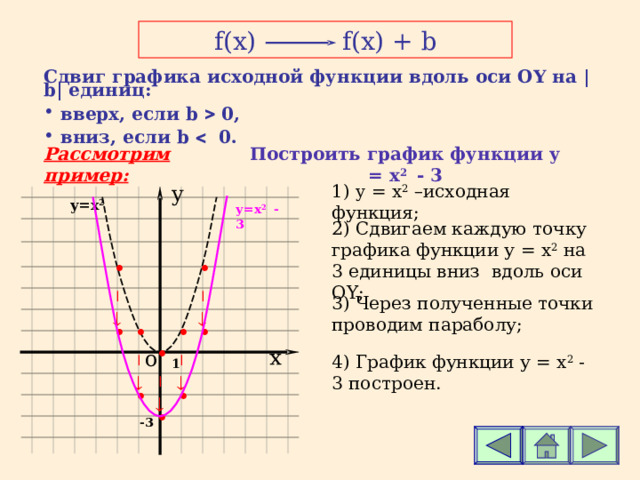
f(x) f(x) + b

Сдвиг графика исходной функции вдоль оси О Y на | b | единиц:

• вверх, если b  0,
• вниз, если b  0.

Построить график функции у = x 2 - 3

Рассмотрим пример:

y

1) y = x 2 – исходная функция;

y=x 2

у= x 2 - 3

2 ) Сдвигаем каждую точку графика функции у = x 2 на 3 единицы вниз вдоль оси О Y ;

•

•









3 ) Через полученные точки проводим параболу;

•

•

•

•









•





о

х

4 ) График функции у = x 2 - 3 построен.

1

•

•

•

-3

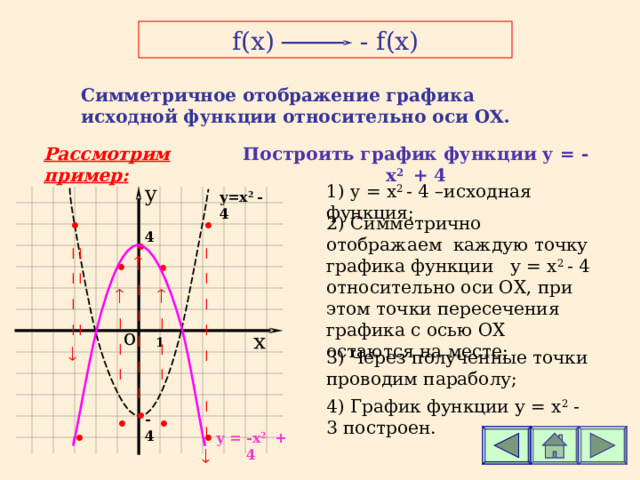
f(x) - f(x)

Симметричное отображение графика исходной функции относительно оси ОХ.

Рассмотрим пример:

Построить график функции у = - x 2 + 4

y

1) y = x 2 - 4 – исходная функция;

y=x 2 - 4

• 

2 ) Симметрично отображаем каждую точку графика функции у = x 2 - 4 относительно оси ОХ, при этом точки пересечения графика с осью ОХ остаются на месте;

• 









4

•



•

•

•









•

•

о

х

1

3 ) Через полученные точки проводим параболу;

4 ) График функции у = x 2 - 3 построен.

-4

•

•

у = - x 2 + 4

f(x) f( | x | )

Симметричное отображение части графика исходной функции, построенной при х  х 0 , относительно прямой х=х 0 , где х 0 – точка смены знака модуля.

Построить график функции у = x 2 - 4 | х |

Рассмотрим пример:

y

1) y = x 2 – 4х – исходная функция, построим ее график при х  0;

у = x 2 – 4х

 ————————————— •

•

2 ) Симметрично отображаем каждую точку части графика функции у = x 2 – 4х, построенной при х  0, относительно прямой х=0;

о

х

2

4

-2

-4

3 ) Через полученные точки проводим кривую;

4 ) График функции у = x 2 – 4х построен.

 ——————— •

•

 — •

•

•

 ————— •

-4

f(x) | f(x) |

Симметричное отображение части графика исходной функции, лежащей под осью ОХ, относительно этой оси.

Рассмотрим пример:

Построить график функции у = | x 2 – 2х – 3 |

1) y = x 2 – 2х – 3 – исходная функция;

y

у = x 2 – 2х – 3

2 ) Симметрично отображаем каждую точку части графика функции у = x 2 – 2х – 3, лежащей под осью ОХ,относительно этой оси;

•

4



•

•

•









•

•

•

•

о

х

3 ) Через полученные точки проводим кривую;

3

-1

4 ) График функции у = x 2 – 2х – 3 построен.

-4

Вам предлагается выполнить построение графиков функций с использованием движения графиков

1 уровень

2 уровень

3 уровень

1 уровень

Постройте график функции с использованием движения графиков:

• y =(x+2) 2 ( f(x)  f(x+a) )
• y = x 2 +1 ( f(x)  f(x) + b )
• y = -x 2 ( f(x)  - f(x) )
• y = | x 2 - 4 | ( f(x)  f(x) + b , f(x)  | f(x) | )

2 уровень

Постройте график функции с использованием движения графиков:

• y = - (x - 1 ) 2 ( f(x)  f(x+a) , f(x)  - f(x) )
• y = | x 2 - 3 | - 1 ( f(x)  f(x) + b , f(x)  - f(x) , f(x)  f(x) + b)
• y = x 2 – 4х + 5

3 уровень

Постройте график функции с использованием движения графиков:

• y = | - ( 3 - x) 2 + 1 |
• y = | x 2 + 4 | х | + 3 |