Эффективность алгоритмов
ПОНЯТЬ
В курсе математики, и уж тем более в жизни, Вы многократно встречались с тем, что одна и та же задача может иметь несколько разных методов решения.
Пример
Квадратное уравнение можно решить методом разложения трёхчлена на сомножители или с помощью дискриминанта.
Переход пешеходов через оживлённую магистраль можно организовать с помощью регулируемого светофором перехода, построив подземный переход или эстакаду над дорогой.
Какой из методов выбрать для программирования? Конечно же, тот, который даёт решение с заданной точностью при минимальных затратах ресурсов. К ресурсам при этом относятся:
время, необходимое для исполнения алгоритма;
объём необходимой памяти;
дополнительное привлечение устройств, программ, файлов.
Время исполнения алгоритма определяется количеством операций (действий), входящих в состав алгоритма, и их сложностью. Например, операция сложения чисел требует меньшего времени, чем операция их умножения; операция присваивания значения переменной осуществляется быстрее, чем операция сравнения.
Объём необходимой памяти зависит от числа переменных и места, занимаемого каждой переменной. Использование множества дополнительных переменных может значительно увеличить объём необходимой памяти.
Обращение в процессе исполнения алгоритма к вспомогательным устройствам и файлам не только увеличивает время выполнения, но и может привести в какой-то момент к сбою в работе программы, ведь устройство может быть выключено, а файл удалён или переименован.
Рассмотрим разные алгоритмы решения одной задачи с целью сравнить их по эффективности. При этом приобретём опыт перехода от словесных формулировок к блок-схемам.
Постановка задачи
Даны три величины A, B, C нужно найти максимальное из них и сохранить его в переменной М.
Заметим, что величины могут быть различного типа. Если это числа, то задача заключается в поиске наибольшего числа; если символы, то - определение символа с наибольшим кодом; если строки, содержащие фамилии, то – определение фамилии, последней по алфавиту. Но сами алгоритмы не зависят от типа величин.
Алгоритм 1.
| Словесная формулировка | Блок-схема |
|
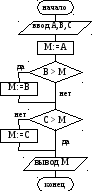
Предположим, что А максимально.
Сравним его с В. Если В больше, то запомним его как максимальное.
Сравним максимальное с С. Если С больше, то запомним его как максимальное.
| 
|
В блок–схеме кроме ввода/вывода есть три операции присваивания и две операции сравнения. Так как исполнение алгоритма при разных значениях А, В и С могут идти по разным «ветвям», то все эти операции будут выполнятся только иногда. Например, при А=1, В=2, С=3. А вот при А=3, В=1, С=2 будет выполнена только одна операция присваивания (М:=А) и две операции сравнения.
Алгоритм 2.
| Словесная формулировка | Блок-схема |
|
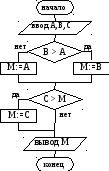
Сравним А с В. Если В больше, то запомним его как максимальное, иначе запомним А как максимальное.
Сравним максимальное с С. Если С больше, то запомним его как максимальное.
| 
|
В блок–схеме также три операции присваивания и две операции сравнения. Но при исполнение алгоритма будут выполнятся или два сравнения и два присваивания (например, при А=1, В=2, С=3), или два сравнения и одно присваивание (например, при А=3, В=1, С=2). То есть при многократном исполнении этот алгоритм более эффективен, чем предыдущий.
Алгоритм 3.
| Словесная формулировка | Блок-схема |
|
Проверим, является ли А максимальным. Если да, то запоминаем его в М, иначе, сравниваем В с С и запоминаем большее из них.
| 
|
В блок–схеме три операции присваивания и три операции сравнения. При исполнение алгоритма будут выполнятся или три сравнения и одно присваивание (например, при А=2, В=1, С=3), или два сравнения и одно присваивание (например, при А=3, В=1, С=2). То есть при многократном исполнении второй алгоритм более эффективен, чем данный.
Алгоритм 4.
| Словесная формулировка | Блок-схема
|
|
Сравниваем попарно величины А, В и С | 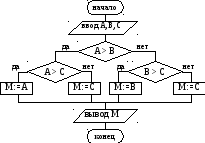
|
Убедитесь, что данный алгоритм при многократном исполнении будет самым эффективным, хотя его блок-схема сложнее, чем блок-схемы предыдущих алгоритмов.
Рассмотренные алгоритмы было легко сравнивать, так как они требуют одной и той же памяти (4 переменных) и не требуют дополнительных ресурсов. То есть сравнение проводилось только по быстродействию при многократном исполнении (среднее количество операций). При решении сложных задач нередки случаи, когда один алгоритм быстрее, но требует больше памяти, а другой медленнее, но обходится меньшими ресурсами. В этом случае сравнивать можно, например, по наиболее важному в каждой конкретной ситуации критерию.
И еще одно важное замечание. Конечно же, нужно заботиться о том, чтобы алгоритм был эффективным. Но если памяти много, процессор достаточно мощный и нет необходимости экономить ресурсы, то нужно выбирать алгоритм, наиболее понятный людям, которые будут его применять, и с которым им будет удобнее всего работать.
ЗНАТЬ
Если существуют разные алгоритмы решения одной и той же задачи, то наиболее эффективным из них будет тот, для выполнения которого требуется меньшие ресурсы компьютера (объём памяти; процессорное время; дополнительные устройства, файлы, программы).
Количество блоков-действий в блок-схеме и количество операций, которые будут выполняться при исполнении алгоритма для конкретных исходных данных, – не одно и то же. В блок-схеме (и в программе) представлены по возможности все возможные действия при разных возможных значениях исходных данных, а при исполнении алгоритма (программы) выполняются только те действия, которые соответствуют конкретным данным, введённым пользователем программы.
УМЕТЬ
1. В параграфе рассматривалась задача поиска максимального из трёх. Предположим, нужно решить задачу упорядочивания значений трёх величин. То есть исходными данными будут А, В и С, а результатом будут три величины: М1, М2 и М3, причём M1 M2 M3. Какой из алгоритмов, рассмотренных в параграфе, наиболее просто дополнить, чтобы решить задачу. Составьте блок-схему алгоритма упорядочивания трёх величин.
2. Необходимо составить алгоритм вычисления х8. Какой из следующих алгоритмов более эффективный?
Каким образом можно вычислить Х15, используя не более пяти операций умножения?
3*** Из курса геометрии Вам известны разные способы вычисления площади треугольника. Например: 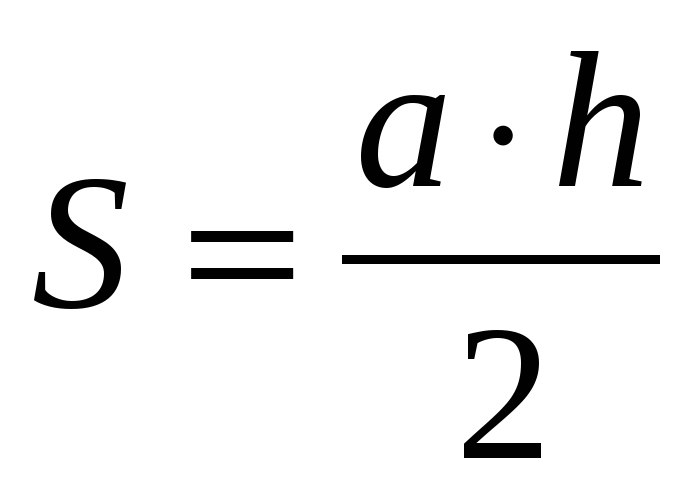 ,
,  ,
, 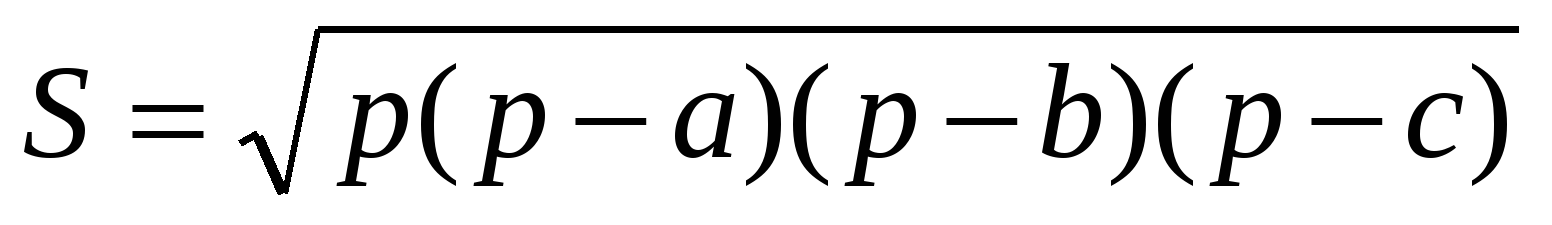 , где а и b – стороны треугольника, h – высота, С – угол, р – полупериметр. Можно ли сравнивать эти способы по эффективности? Ответ обоснуйте.
, где а и b – стороны треугольника, h – высота, С – угол, р – полупериметр. Можно ли сравнивать эти способы по эффективности? Ответ обоснуйте.
ПРАКТИКУМ
Работа в среде программирования Pascal. Операторы ввода и вывода.
В языки программирования включены разнообразные средства для организации вывода информации на экран.
В Pascal вывод текстовой и графической информации производится разными способами и имеет свои особенности.
Текстовый экран представляет собой таблицу 80х25, в каждой позиции которой может быть отображен один из возможных символов таблицы кодировки.

Формат оператора ввода: read (имя_переменной1, имя_переменной2, …);
Формат оператора вывода: write (параметр1, параметр2, …);
Параметрами оператора вывода могут быть:
поясняющий текст в апострофах (выводится неизменно);
константа (выводится неизменно);
имя переменной (выводится значение переменной);
выражение (вычисляется и выводится значение выражения).
Операторы write и writeln допускают также явное указание количества экранных позиций для вывода значения параметра, чтобы выводимые значения не «сливались» друг с другом, а размещались с заданным промежутком между ними. Экранные позиции задаются после параметра через двоеточие.
Операторы ввода и вывода используются также в виде readln (список имен переменных); и writeln (список параметров);. Добавление «ln» (от line –линия) в конце слов read и write означает, что после выполнения этих операторов курсор будет установлен в начало следующей строки рабочего экрана.
Указать конкретную позицию курсора при вводе/выводе можно с помощью процедуры gotoxy(Nk , Ns);, где Nk – номер колонки (от 1 до 80), Ns – номер строки (от 1 до 25).
Цвет выводимых сообщений можно задать с помощью процедуры Textcolor(номер цвета). Номера цветов можно задавать числами от 0 до 15 или их названиями на английском языке: 0 (black) – чёрный, 1 (blue) – синий, 2 (green) – зелёный и т.д. до 15 (white) – белый.
Эти стандартные процедуры размещаются обычно в библиотеке CRT, которую надо подключить в начале программы.
| 1 | Найдите ошибки в записи следующих операторов: а) read (‘a=’, a); б) write (‘a=, a); в) writln (‘a=’, a); г) gotoxy(100, 30); |
| 2 | Подумайте и затем проверьте, что будет на экране после выполнения операторов (переменную а опишите как переменную вещественного типа): а) write (‘a’, a, a0, (a+2)*2); б) writeln (‘a=’, a : 5, ‘a+2=’ : 6, a+2 : 5); в) writeln (true |
| 3 | Введите и отладьте программы, которые вычисляют, подобно калькулятору, квадратный корень из введенного пользователем числа. Объясните, в чём преимущество каждой из них. Program v1; Uses Crt; Var x: Real; Begin ReadLn(x); WriteLn(sqrt(x)); End.
Program v2; Uses Crt; Var x: Real; Begin ClrScr; WriteLn(’Программа вычисляет квадратный корень’); Repeat Write(’Пожалуйста, введите неотрицательное число’); ReadLn(x); Until x = 0; WriteLn(’Значение корня из числа равно ’,sqrt(x):10:5); End. |
| 4 | Составьте и отладьте программы для решения следующих задач. От пользователя ввести имя и год его рождения и вывести на экран сообщение «Вам, имя, возраст лет», например: «Вам, Сережа, 15 лет». Дана сторона квадрата. Найти его периметр и площадь. Дан радиус круга, найти его площадь и длину окружности. Даны катеты прямоугольного треугольника. Найти его периметр и площадь. Дана температура по шкале Цельсия. Определить, чему она равна по шкалам Фаренгейта и Кельвина. (ТС = 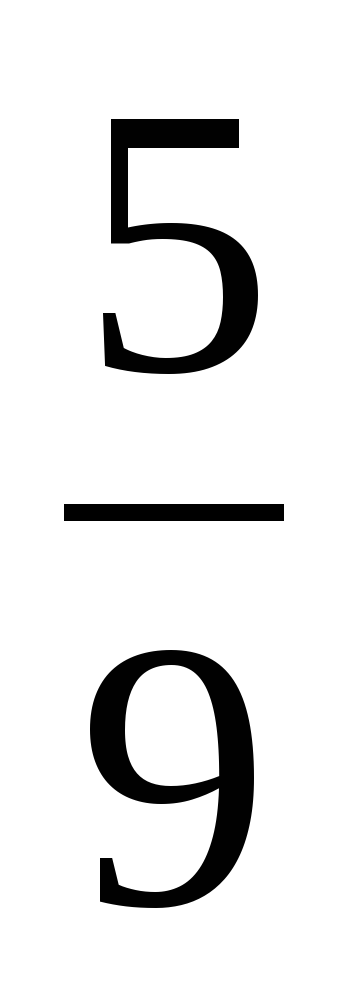 (ТФ – 32); ТС = ТК – 273о) (ТФ – 32); ТС = ТК – 273о) Два автомобиля находятся на расстоянии S и разъезжаются со скоростями V1 и V2. Определить, на каком расстоянии они будут друг от друга через T часов. |
7