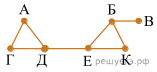РЕШУ ЕГЭ — информатика
Вариант № 17007942
1. Тип 1 № 13399 
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах.
| П1 | П2 | П3 | П4 | П5 | П6 | П7 |
| П1 | | 10 | | | | | 12 |
| П2 | 10 | | | | | | 8 |
| П3 | | | | | 11 | 15 | |
| П4 | | | | | | 5 | |
| П5 | | | 11 | | | 13 | 6 |
| П6 | | | 15 | 5 | 13 | | |
| П7 | 12 | 8 | | | 6 | | |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги из пункта Б в пункт Е. В ответе запишите целое число.
ВНИМАНИЕ! Длины отрезков на схеме не отражают длины дорог.
2. Тип 2 № 27228 
Логическая функция F задаётся выражением (¬x ∨ y ∨ z) ≡ (¬y ∧ z ∧ w). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| ? | ? | ? | ? | F |
| 1 | 1 | 1 | 1 |
| 0 | 0 | | 1 |
| 1 | | 1 | 1 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
3. Тип 3 № 72561 
В файле приведён фрагмент базы данных «Продукты», содержащей информацию о поставках товаров и их продаже. База данных состоит из трёх таблиц.
3.xlsx
Таблица «Торговля» содержит записи о поставках и продажах товаров в магазинах города в июне 2021 г. Таблица «Товар» содержит данные о товарах. Таблица «Магазин» содержит данные о магазинах. На рисунке приведена схема базы данных, содержащая все поля каждой таблицы и связи между ними.
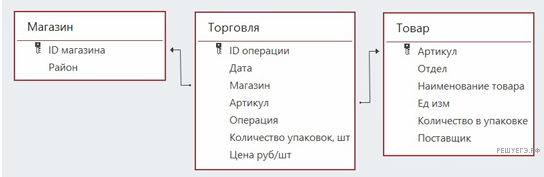
Используя информацию из приведённой базы данных, определите, сколько всего литров всех видов сметаны было поставлено в магазины Центрального района в период с 5 по 9 июня включительно. В ответе запишите число — найденное количество литров.
4. Тип 4 № 27263 
По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 000, Б — 01, В — 1101, Г — 111, Д — 0010, Е — 100. Какое наименьшее количество двоичных знаков потребуется для кодирования слова КОКОС?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
5. Тип 5 № 9792 
Автомат получает на вход трёхзначное число. По этому числу строится новое число по следующим правилам.
1. Перемножаются первая и вторая, а также вторая и третья цифры.
2. Полученные два числа записываются друг за другом в порядке неубывания без разделителей.
Пример. Исходное число: 631. Произведение: 6 · 3 = 18; 3 · 1 = 3. Результат: 318.
Укажите наибольшее число, при обработке которого автомат выдаёт результат 621.
6. Тип 6 № 59684 
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится B начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 6 команд: Поднять хвост, означающая переход к перемещению 6eз рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n — целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m — целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись Повтори k [Команда1 Команда2 ... КомандаS] означает, что последовательность из S команд повторится k раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 2 [Вперёд 10 Направо 90 Вперёд 18 Направо 90]
Поднять хвост
Вперёд 5 Направо 90 Вперёд 7 Налево 90
Опустить хвост
Повтори 2 [Вперёд 10 Направо 90 Вперёд 7 Направо 90].
Определите, сколько точек с целочисленными координатами будут находиться внутри объединения фигур, ограниченных заданными алгоритмом линиями, включая точки на линиях.
7. Тип 7 № 10497 
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 1024 x 1024 пикселей при условии, что в изображении могут использоваться 16 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
8. Тип 8 № 33180 
Тимофей составляет 5-буквенные коды из букв Т, И, М, О, Ф, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой И. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Тимофей?
9. Тип 9 № 45243 
Откройте файл электронной таблицы, содержащей в каждой строке пять натуральных чисел.
9.xlsx
Определите количество строк таблицы, в которых квадрат суммы максимального и минимального чисел в строке больше суммы квадратов трёх оставшихся.
10. Тип 10 № 35984 
Определите, сколько раз в тексте произведения А. С. Пушкина «Дубровский» встречается существительное «застава» в любом числе и падеже.
Задание 10
11. Тип 11 № 13740 
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 10 символов. В качестве символов используют прописные буквы латинского алфавита, то есть 26 различных символов. В базе данных для хранения каждого пароля отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Определите объём памяти (в байтах), необходимый для хранения данных о 50 пользователях. В ответе запишите только целое число — количество байт.
12. Тип 12 № 13544 
Исполнитель Редактор получает на вход строку цифр и преобразует её.
Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Цикл ПОКА условие последовательность команд КОНЕЦ ПОКА выполняется, пока условие истинно. В конструкции ЕСЛИ условие ТО команда1 ИНАЧЕ команда2 КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Ниже приведена программа для исполнителя Редактор.
НАЧАЛО ПОКА нашлось (19) ИЛИ нашлось (299) ИЛИ нашлось (3999) заменить (19, 2) заменить (299, 3) заменить (3999, 1) КОНЕЦ ПОКА КОНЕЦ
На вход этой программе подаётся строка длины 94, состоящая из цифры 3, за которой следуют 93 идущих подряд цифр 9.
Какая строка получится в результате применения программы к этой строке?
13. Тип 13 № 2225 
На сервере info.edu находится файл exam.net, доступ к которому осуществляется по протоколу http. Фрагменты адреса данного файла закодированы буквами а, Ь, с ... g (см. таблицу). Запишите последовательность этих букв, которая кодирует адрес указанного файла в Интернете.
| a | info |
| b | / |
| c | .net |
| d | .edu |
| e | http |
| f | exam |
| g | :// |
14. Тип 14 № 15984 
Значение выражения 912 + 38 − 3? записали в системе счисления с основанием 3.
Сколько цифр 2 содержится в этой записи?
15. Тип 15 № 35904 
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наименьшего натурального числа А формула
ДЕЛ(A, 40) ∧ (ДЕЛ(780, x) → (¬ДЕЛ(A, x) → ¬ДЕЛ(180, x)))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?
16. Тип 16 № 4643 
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(1) = 1;
F(n) = 5 · F(n – 1) + 3 · n при n 1.
Чему равно значение функции F(4)? В ответе запишите только натуральное число.
17. Тип 17 № 37355 
В файле содержится последовательность из 10 000 целых положительных чисел. Каждое число не превышает 10 000. Определите и запишите в ответе сначала количество пар элементов последовательности, у которых сумма элементов кратна 7, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два различных элемента последовательности. Порядок элементов в паре не важен.
17.txt
Ответ:
18. Тип 18 № 58485 
Робот стоит в левом верхнем углу прямоугольного поля, в каждой клетке которого записано целое положительное число. За один ход робот может переместиться на одну клетку вправо или на одну клетку вниз.
Расход энергии на запуск робота равен числу, записанному в стартовой клетке. В дальнейшем расход энергии на шаг из одной клетки в другую равен абсолютной величине разности чисел, записанных в этих клетках.
Определите минимальный и максимальный расход энергии при переходе робота в правую нижнюю клетку поля. В ответе запишите два числа: сначала минимальный расход энергии, затем — максимальный.
Исходные данные записаны в электронной таблице. Пример входных данных (для таблицы размером 4 × 4):
Задание 18
| 45 | 54 | 20 | 86 |
| 68 | 46 | 27 | 71 |
| 83 | 26 | 98 | 82 |
| 23 | 80 | 25 | 48 |
При указанных входных данных минимальное значение получится при движении по маршруту 45 → 54 → 46 → 27 → 71 → 82 → 48. Расход энергии на этом пути равен:
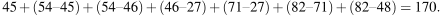
Максимальное значение получится при движении по маршруту 45 → 68 → 83 → 26 → 98 → 25 → 48, расход энергии в этом случае равен 308.
В ответе в данном примере надо записать числа 170 и 308.
Ответ:
19. Тип 19 № 56547 
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в меньшую кучу любое количество камней от одного до количества камней в этой куче. Изменять количество камней в большей куче не разрешается. Если кучи содержат равное количество камней, добавлять камни можно в любую из них. Пусть, например, в начале игры в первой куче 3 камня, а во второй — 5 камней, будем обозначать такую позицию (3, 5). Петя первым ходом должен добавить в первую кучу от 1 до 3 камней, он может получить позиции (4, 5), (5, 5) и (6, 5). Если Петя создаёт позицию (4, 5), то Ваня своим ходом может добавить от 1 до 4 камней в первую кучу, а если Петя создаёт позицию (6, 5), то Ваня может добавить от 1 до 5 камней во вторую кучу, так как теперь она стала меньшей. В позиции (5, 5) Ваня может добавить от 1 до 5 камней в любую кучу.
Игра завершается, когда общее количество камней в кучах становится более 39. Победителем считается игрок, сделавший последний ход, то есть первым получивший 40 или больше камней в двух кучах.
Известно, что Петя смог выиграть первым ходом. Какое наименьшее число камней могло быть суммарно в двух кучах?
20. Тип 20 № 56548 
В игре, описанной в задании 19, в начальный момент в первой куче было 4 камня, а во второй — S камней, 1 ≤ S ≤ 35.
Укажите минимальное и максимальное из таких значений S, при которых Петя не может выиграть первым ходом, но у Пети есть выигрышная стратегия, позволяющая ему выиграть вторым ходом при любой игре Вани.
В ответе запишите сначала минимальное значение, затем максимальное.
Ответ:
21. Тип 21 № 56549 
В игре, описанной в задании 19, в начальный момент в первой куче было 4 камня, а во второй — S камней, 1 ≤ S ≤ 35.
Найдите минимальное из таких значений S, при котором у Вани есть стратегия, позволяющая ему выиграть вторым ходом при любой игре Пети, но у Вани нет стратегии, которая позволяла бы ему гарантированно выиграть первым ходом.
22. Тип 22 № 47603 
В файле 22_22.xlsx содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы — время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) | ID процесса(ов) A |
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1;2 |
| 4 | 7 | 3 |
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 — через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
23. Тип 23 № 18801 
Исполнитель Вычислитель преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера.
1. Прибавить 1.
2. Умножить на 3.
3. Прибавить 2.
Первая команда увеличивает число на экране на 1, вторая умножает его на 3, третье увеличивает его на 2.
Программа для исполнителя Вычислитель — это последовательность команд.
Сколько существует программ, которые преобразуют исходное число 2 в число 12 и при этом траектория вычислений содержит числа 9 и 11?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 10, 30.
24. Тип 24 № 27693 
Текстовый файл состоит не более чем из 106 символов A, B и C. Определите максимальное количество идущих подряд символов C.
Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.
Задание 24
25. Тип 25 № 47022 
Пусть M (N) — пятый по величине делитель натурального числа N без учёта самого числа и единицы. Например, M(1000) = 100.
Если у числа N меньше 5 различных делителей, не считая единицы и самого числа, считаем, что M (N) = 0.
Найдите 5 наименьших натуральных чисел, превышающих 300 000 000, для которых M (N) 0. В ответе запишите найденные значения M (N) в порядке возрастания соответствующих им чисел N.
Ответ:
Примечание.
Пятый по величине делитель — пятый делитель из пяти наибольших делителей числа. То есть для числа 1000 пять наибольших делителей, не считая единицы и самого числа, — 500, 250, 200, 125, 100, пятый по величине — 100.
26. Тип 26 № 48474 
На складе хранятся кубические контейнеры различного размера. Чтобы сократить занимаемое при хранении место, контейнеры вкладывают друг в друга. Один контейнер можно вложить в другой, если размер стороны внешнего контейнера превышает размер стороны внутреннего на 7 и более условных единиц. Группу вложенных друг в друга контейнеров называют блоком. Количество контейнеров в блоке может быть любым. Каждый блок, независимо от количества и размера входящих в него контейнеров, а также каждый одиночный контейнер, не входящий в блоки, занимает при хранении одну складскую ячейку.
Зная количество контейнеров и их размеры, определите минимальное количество ячеек для хранения всех контейнеров и максимально возможное количество контейнеров в одном блоке.
Задание 26
Входные данные.
Первая строка входного файла содержит целое число N — общее количество контейнеров. Каждая из следующих N строк содержит натуральное число, не превышающее 10 000, — размер контейнера в условных единицах.
В ответе запишите два целых числа: сначала минимальное количество ячеек для хранения всех контейнеров, затем максимально возможное количество контейнеров в одном блоке.
Ответ:
27. Тип 27 № 47024 
Дана последовательность натуральных чисел. Необходимо определить количество её непрерывных подпоследовательностей, сумма элементов которых кратна 1111.
Входные данные.
Файл A
Файл B
Первая строка входного файла содержит целое число N — общее количество чисел в наборе. Каждая из следующих N строк содержит одно число. Гарантируется, что общая сумма всех чисел и число в ответе не превышают 2 · 109 по абсолютной величине.
Вам даны два входных файла (A и B), каждый из которых имеет описанную выше структуру. В ответе укажите два числа: сначала значение искомой суммы для файла A, затем для файла B.
Ответ: