РЕШУ ЕГЭ — информатика
Вариант № 17007937
1. Тип 1 № 13533 
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах.
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | П8 |
| П1 | | 15 | | 20 | | | | 18 |
| П2 | 15 | | 25 | | | | | |
| П3 | | 25 | | | | 24 | | 22 |
| П4 | 20 | | | | | | 12 | |
| П5 | | | | | | 13 | 16 | 17 |
| П6 | | | 24 | | 13 | | | 15 |
| П7 | | | | 12 | 16 | | | |
| П8 | 18 | | 22 | | 17 | 15 | | |
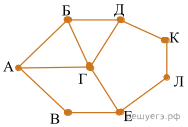
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги от пункта В до пункта Е. В ответе запишите целое число.
2. Тип 2 № 16805 
Логическая функция F задаётся выражением (¬x ≡ z) → (y ≡ (w ∨ x)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
| ??? | ??? | ??? | ??? | F |
| 0 | 0 | | | 0 |
| 0 | | | 0 | 0 |
| 0 | | 0 | 0 | 0 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 1 | Функция |
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
3. Тип 3 № 61383 
В файле приведён фрагмент базы данных «Продукты», содержащей информацию о поставках товаров и их продаже. База данных состоит из трёх таблиц.
Задание 3
Таблица «Торговля» содержит записи о поставках и продажах товаров в магазинах города в июне 2021 г. Таблица «Товар» содержит данные о товарах. Таблица «Магазин» содержит данные о магазинах.
На рисунке приведена схема базы данных, содержащая все поля каждой таблицы и связи между ними.

Используя информацию из приведённой базы данных, определите общую прибыль, полученную за месяц магазинами Заречного района от торговли всеми видами кофе.
Под прибылью в этой задаче понимается разница между стоимостью продажи и стоимостью поставки товаров.
В ответе запишите число — найденную прибыль в рублях.
4. Тип 4 № 11341 
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0; для буквы Б — кодовое слово 10. Какова наименьшая возможная сумма длин всех шести кодовых слов?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
5. Тип 5 № 11262 
Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются отдельно первая и вторая цифры, вторая и третья цифры, а также третья и четвёртая цифры.
2. Из полученных трёх чисел выбираются два наибольших и записываются друг за другом в порядке неубывания без разделителей.
Пример. Исходное число: 9575. Суммы: 9 + 5 = 14; 5 + 7 = 12; 7 + 5 = 12. Наибольшие суммы: 14, 12. Результат: 1214.
Укажите наименьшее число, при обработке которого автомат выдаёт результат 1517.
6. Тип 6 № 47390 
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм: Повтори 12 [Направо 60 Вперёд 1 Направо 60 Вперёд 1 Направо 270].
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
7. Тип 7 № 45241 
Для хранения сжатого произвольного растрового изображения размером 192 на 960 пикселей отведено 90 Кбайт памяти без учёта размера заголовка файла. При сжатии объём файла уменьшается на 35%. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?
8. Тип 8 № 9760 
Алексей составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Алексей использует 5-буквенные слова, в которых есть только буквы A, B, C, X, причём буква X может появиться на первом месте или не появиться вовсе. Сколько различных кодовых слов может использовать Алексей?
9. Тип 9 № 72594 
В каждой строке электронной таблицы записаны шесть натуральных чисел.
Определите количество строк таблицы, содержащих числа, для которых одновременно выполнены все следующие условия:
— в строке есть число, повторяющееся не меньше трёх раз;
— в строке есть число, не повторяющееся в этой строке;
— среднее арифметическое всех повторяющихся чисел строки (с учётом количества повторений) меньше среднего арифметического неповторяющихся чисел этой строки.
В ответе запишите число — количество строк, удовлетворяющих заданным условиям.
Задание 9
10. Тип 10 № 27583 
С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «Онегин» в тексте романа в стихах А. С. Пушкина «Евгений Онегин». Другие формы слова «Онегин», такие как «Онегина», «Онегиным» и т. д., учитывать не следует. В ответе укажите только число.
Задание 10
11. Тип 11 № 7195 
Для регистрации на сайте некоторой страны пользователю требуется придумать пароль. Длина пароля — ровно 7 символов. В качестве символов используются десятичные цифры и 30 различных букв местного алфавита, причём все буквы используются в двух начертаниях: как строчные, так и прописные (регистр буквы имеет значение!). Под хранение каждого такого пароля на компьютере отводится минимально возможное и одинаковое целое количество байтов, при этом используется посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством битов. Определите объём памяти, который занимает хранение 40 паролей. (Ответ дайте в байтах.)
12. Тип 12 № 15630 
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр:
1) заменить (v, w);
2) нашлось (v).
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w, вторая проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из одной единицы и 75 стоящих справа от нее нулей? В ответе запишите сколько нулей будет в конечной строке.
НАЧАЛО
ПОКА нашлось (10) ИЛИ нашлось (1)
ЕСЛИ нашлось (10)
ТО заменить (10, 001)
ИНАЧЕ заменить (1, 00)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
13. Тип 13 № 13515 
В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая — к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес, — в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого разряда — нули. Адрес сети получается в результате применения поразрядной конъюнкции к заданным IP-адресу узла и маске.
Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.
Для узла с IP-адресом 119.83.208.27 адрес сети равен 119.83.192.0. Каково наибольшее возможное количество единиц в разрядах маски?
14. Тип 14 № 15111 
Значение выражения 255 + 514 − 5? записали в системе счисления с основанием 5. Сколько цифр 4 содержится в этой записи?
15. Тип 15 № 9804 
Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n.
Так, например, 14 & 5 = 11102 & 01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула
x & 29 ≠ 0 → (x & 17 = 0 → x & А ≠ 0)
тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной x)?
16. Тип 16 № 4658 
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(1) = 1;
F(2) = 1;
F(n) = F(n–1) * n − 2 * F(n–2) при n 2.
Чему равно значение функции F(6)? В ответе запишите только натуральное число.
17. Тип 17 № 37358 
В файле содержится последовательность из 10 000 целых положительных чисел. Каждое число не превышает 10 000. Определите и запишите в ответе сначала количество пар элементов последовательности, у которых сумма элементов кратна 10, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два различных элемента последовательности. Порядок элементов в паре не важен.
17.txt
Ответ:
18. Тип 18 № 38952 
Робот стоит в левом верхнем углу прямоугольного поля, в каждой клетке которого записано натуральное число. За один ход робот может переместиться на одну клетку вправо или на одну клетку вниз. Выходить за пределы поля робот не может. В начальный момент запас энергии робота равен числу, записанному в стартовой клетке. После каждого шага робота запас энергии изменяется по следующим правилам: если число в очередной клетке больше, чем в предыдущей, запас увеличивается на величину этого числа, если меньше — уменьшается на эту же величину.
Определите максимальный и минимальный запас энергии, который может быть у робота после перехода в правую нижнюю клетку поля. В ответе запишите два числа: сначала максимально возможное значение, затем минимальное.
Исходные данные записаны в электронной таблице.
Задание 18
Пример входных данных (для таблицы размером 4 × 4):
| 200 | 8 | 69 | 50 |
| 87 | 35 | 7 | 17 |
| 32 | 1 | 9 | 32 |
| 44 | 12 | 80 | 43 |
При указанных входных данных максимальное значение получается при движении по маршруту 200 − 8 + 69 − 7 + 17 + 32 + 43 = 346, а минимальное при движении по маршруту 200 − 87 − 35 − 7 + 9 + 80 − 43 = 117.
Ответ:
19. Тип 19 № 56519 
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в меньшую кучу любое количество камней от одного до количества камней в этой куче. Изменять количество камней в большей куче не разрешается. Если кучи содержат равное количество камней, добавлять камни можно в любую из них. Пусть, например, в начале игры в первой куче 3 камня, а во второй — 5 камней, будем обозначать такую позицию (3, 5). Петя первым ходом должен добавить в первую кучу от 1 до 3 камней, он может получить позиции (4, 5), (5, 5) и (6, 5). Если Петя создаёт позицию (4, 5), то Ваня своим ходом может добавить от 1 до 4 камней в первую кучу, а если Петя создаёт позицию (6, 5), то Ваня может добавить от 1 до 5 камней во вторую кучу, так как теперь она стала меньшей. В позиции (5, 5) Ваня может добавить от 1 до 5 камней в любую кучу.
Игра завершается, когда общее количество камней в кучах становится более 45. Победителем считается игрок, сделавший последний ход, то есть первым получивший 46 или больше камней в двух кучах.
Известно, что Петя смог выиграть первым ходом. Какое наименьшее число камней могло быть суммарно в двух кучах?
20. Тип 20 № 56520 
В игре, описанной в задании 19, в начальный момент в первой куче было 5 камней, а во второй — S камней, 1 ≤ S ≤ 40. Укажите минимальное и максимальное из таких значений S, при которых Петя не может выиграть первым ходом, но у Пети есть выигрышная стратегия, позволяющая ему выиграть вторым ходом при любой игре Вани.
В ответе запишите сначала минимальное значение, затем максимальное.
21. Тип 21 № 56521 
В игре, описанной в задании 19, в начальный момент в первой куче было 5 камней, а во второй — S камней, 1 ≤ S ≤ 40.
Найдите минимальное из таких значений S, при котором у Вани есть стратегия, позволяющая ему выиграть вторым ходом при любой игре Пети, но у Вани нет стратегии, которая позволяла бы ему гарантированно выиграть первым ходом.
22. Тип 22 № 61402 
В компьютерной системе необходимо выполнить некоторое количество вычислительных процессов, которые могут выполняться параллельно или последовательно. Для запуска некоторых процессов необходимы данные, которые получаются как результаты выполнения одного или двух других процессов — поставщиков данных. Все независимые процессы (не имеющие поставщиков данных) запускаются в начальный момент времени. Если зависимый процесс получает данные от одного или нескольких других процессов (поставщиков данных), то выполнение зависимого процесса начинается сразу же после завершения последнего из процессов-поставщиков. Количество одновременно выполняемых процессов может быть любым, длительность процесса не зависит от других параллельно выполняемых процессов.
Задание 22
В таблице представлены идентификатор (ID) каждого процесса, его длительность и ID поставщиков данных для зависимых процессов.
Определите суммарную длительность всех промежутков времени, в течение которых выполнялось ровно 3 процесса.
23. Тип 23 № 13552 
Исполнитель Осень16 преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера.
1. Прибавить 1.
2. Прибавить 2.
3. Прибавить 4.
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2, третья — увеличивает на 4.
Программа для исполнителя Осень16 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 15 и при этом траектория вычислений содержит число 8?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 10, 11.
24. Тип 24 № 37131 
Текстовый файл содержит только заглавные буквы латинского алфавита (ABC…Z). Определите наибольшую длину цепочки символов, среди которых нет символов K и L, стоящих рядом.
Например, в тексте ABCAABAKLD самая длинная цепочка символов, удовлетворяющая условию, — ABCAABAK, её длина равна 8.
Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.
Задание 24
25. Тип 25 № 37130 
Напишите программу, которая перебирает целые числа, большие 600 000, в порядке возрастания и ищет среди них такие, среди делителей которых есть хотя бы одно число, оканчивающееся на 7, но не равное 7 и самому числу. Необходимо вывести первые 5 таких чисел, и наименьший делитель, оканчивающийся на 7, не равный 7 и самому числу.
Формат вывода: для каждого из 5 таких найденных чисел в отдельной строке сначала выводится само число, затем — наименьший делитель, оканчивающийся на 7, не равный 7 и самому числу. Строки выводятся в порядке возрастания найденных чисел.
Количество строк в таблице для ответа избыточно.
Ответ:
26. Тип 26 № 47023 
При проведении эксперимента заряженные частицы попадают на чувствительный экран, представляющий из себя матрицу размером 10 000 на 10 000 точек. При попадании каждой частицы на экран в протоколе фиксируются координаты попадания: номер ряда (целое число от 1 до 10 000) и номер позиции в ряду (целое число от 1 до 10 000).
Точка экрана, в которую попала хотя бы одна частица, считается светлой, точка, в которую ни одна частица не попала, — тёмной.
При анализе результатов эксперимента рассматривают группы светлых точек, расположенных в одном ряду так, что между каждыми двумя соседними светлыми точками находится ровно одна тёмная.
Вам необходимо по заданному протоколу определить максимальную длину такой группы и номер ряда, в котором эта группа встречается. Если таких рядов несколько, укажите минимально возможный номер.
Входные данные.
Задание 26
Первая строка входного файла содержит целое число N — общее количество частиц, попавших на экран. Каждая из следующих N строк содержит 2 целых числа: номер ряда и номер позиции в ряду.
В ответе запишите два целых числа: сначала максимальную длину непрерывной группы светлых точек, затем — номер ряда, в котором эта группа встречается.
Ответ:
27. Тип 27 № 27990 
На вход программы поступает последовательность из N целых положительных чисел. Рассматриваются все пары различных элементов последовательности (элементы пары не обязаны стоять в последовательности рядом, порядок элементов в паре неважен). Необходимо определить количество пар, для которых произведение элементов кратно 62.
Входные данные.
Файл A
Файл B
В первой строке входных данных задаётся количество чисел N (1 ≤ N ≤ 60 000). В каждой из последующих N строк записано одно натуральное число, не превышающее 10 000. В качестве результата программа должна вывести одно число: количество пар, в которых произведение элементов кратно 62.
Пример организации исходных данных во входном файле:
5
2
6
13
31
93
Пример выходных данных для приведённого выше примера входных данных:
4
В ответе укажите два числа: сначала значение искомой суммы для файла А, затем для файла B.
Ответ:
Пояснение. Из 5 чисел можно составить 4 пары, удовлетворяющие условию. Для заданного набора чисел получаем пары (2, 31), (2, 93), (6, 31), (6, 93).































