Тип 1 № 68234 
На рисунке схема дорог изображена в виде графа, в таблице указано время в пути (в минутах) по каждой дороге. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите минимальное время перемещения по данным дорогам из пункта А в пункт Д. В ответе укажите целое число: минимальное время в минутах.
|
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | П8 | П9 |
| П1 |
| 34 |
| 32 |
|
|
|
|
|
| П2 | 34 |
|
| 31 |
| 50 |
| 26 |
|
| П3 |
|
|
| 39 | 37 |
|
|
|
|
| П4 | 32 | 31 | 39 |
|
|
|
|
| 41 |
| П5 |
|
| 37 |
|
|
| 21 |
| 44 |
| П6 |
| 50 |
|
|
|
|
| 35 | 23 |
| П7 |
|
|
|
| 21 |
|
|
| 20 |
| П8 |
| 26 |
|
|
| 35 |
|
|
|
| П9 |
|
|
| 41 | 44 | 23 | 20 |
|
|
2. Тип 2 № 35891 
Логическая функция F задаётся выражением (y → z) ∧ ¬((y ∨ w) → (z ∧ x)). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
| 1 | 1 |
| 1 | 1 |
|
| 1 | 1 |
| 1 |
| 1 | 1 |
|
| 1 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 2 | Функция |
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
3. Тип 3 № 48451 
В файле приведён фрагмент базы данных «Продукты», содержащей информацию о поставках товаров и их продаже. База данных состоит из трёх таблиц.
Задание 3
Таблица «Торговля» содержит записи о поставках и продажах товаров в магазинах города в июне 2021 г. Таблица «Товар» содержит данные о товарах. Таблица «Магазин» содержит данные о магазинах.
На рисунке приведена схема базы данных, содержащая все поля каждой таблицы и связи между ними.

Используя информацию из приведённой базы данных, определите общую сумму выручки, полученную от продаж продуктов отдела «Бакалея» в магазинах Первомайского района с 14 по 20 июня.
В ответе запишите число — найденную сумму выручки в рублях.
4. Тип 4 № 26948 
Для кодирования некоторой последовательности, состоящей только из букв А, Б, В, Г, Д, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В использовали соответственно кодовые слова 1, 00, 0100. Укажите минимальную возможную суммарную длину для букв Г и Д, если известно, что код должен допускать однозначное декодирование.
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
5. Тип 5 № 18434 
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа ещё два разряда по следующему правилу:
а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия — справа дописывается остаток от деления суммы её цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите минимальное число R, которое превышает число 55 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.
6. Тип 6 № 70533 
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится B начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 6 команд: Поднять хвост, означающая переход к перемещению 6eз рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n — целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m — целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись Повтори k [Команда1 Команда2 ... КомандаS] означает, что последовательность из S команд повторится k раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 9 [Вперёд 22 Направо 90 Вперёд 6 Направо 90]
Поднять хвост
Вперёд 1 Направо 90 Вперёд 5 Налево 90
Опустить хвост
Повтори 9 [Вперёд 53 Направо 90 Вперёд 75 Направо 90].
Определите периметр области пересечения фигур, ограниченных заданными алгоритмом линиями.
7. Тип 7 № 48428 
Музыкальный фрагмент был записан в формате стерео (двухканальная запись), оцифрован с частотой дискретизации 44 кГц и разрешением 16 бит и сохранён без использования сжатия данных. Получился файл размером 120 Мбайт. Затем тот же фрагмент был записан в формате квадро (четырёхканальная запись) с частотой дискретизации 88 кГц и тоже сохранён без сжатия, при этом получился файл размером 720 Мбайт. С каким разрешением проводилась вторая запись? В ответе укажите целое число — разрешение в битах, единицу измерения писать не нужно.
8. Тип 8 № 14225 
Олег составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Олег использует 4-буквенные слова, в которых есть только буквы A, B, C, D, E, X, Z, причём буквы X и Z встречаются только на двух первых позициях, а буквы A, B, C, D, E — только на двух последних. Сколько различных кодовых слов может использовать Олег?
9. Тип 9 № 38588 
Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа.
9.xlsx
Выясните, какое количество троек чисел может являться сторонами треугольника, то есть удовлетворяет неравенству треугольника. В ответе запишите только число.
10. Тип 10 № 59688 
С помощью текстового редактора определите, сколько раз встречается сочетание букв «дом» или «Дом» только в составе других слов, но не как отдельное слово, в тексте повести А. И. Куприна «Поединок». В ответе укажите только число.
Задание 10
11. Тип 11 № 10414 
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 20 символов и содержащий только символы из 10-символьного набора: А, В, C, D, Е, F, G, H, K, L. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено целое число байт, одно и то же для всех пользователей.
Для хранения сведений о 20 пользователях потребовалось 400 байт. Сколько байт выделено для хранения дополнительных сведений об одном пользователе? В ответе запишите только целое число — количество байт.
12. Тип 12 № 46970 
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка
исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно).
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Дана программа для редактора:
НАЧАЛО
ПОКА НЕ нашлось (00)
заменить (01, 210)
заменить (02, 3101)
заменить (03, 2012)
КОНЕЦ ПОКА
КОНЕЦ
Известно, что исходная строка начиналась с нуля и заканчивалась нулём, а между ними содержала только единицы, двойки и тройки. После выполнения данной программы получилась строка, содержащая 70 единиц, 56 двоек и 23 тройки. Сколько цифр было в исходной строке?
13. Тип 13 № 11348 
В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая — к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес, — в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого разряда — нули. Адрес сети получается в результате применения поразрядной конъюнкции к заданным IP-адресу узла и маске.
Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.
Для узла с IP-адресом 119.83.208.27 адрес сети равен 119.83.192.0. Каково наименьшее возможное количество единиц в разрядах маски?
14. Тип 14 № 48376 
Операнды арифметического выражения записаны в системе счисления с основанием 16:
8x83416 + 44x2716.
В записи чисел переменной x обозначена неизвестная цифра из алфавита шестнадцатеричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 23. Для найденного значения x вычислите частное от деления значения арифметического выражения на 23 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
15. Тип 15 № 34540 
На числовой прямой даны два отрезка: Р = [12, 62] и Q = [52, 92]. Какова наименьшая возможная длина интервала A, что логическое выражение
¬(¬(х ∈ А) ∧ (х ∈ Р)) ∨ (х ∈ Q)
тождественно истинно, то есть принимает значение 1 при любом значении переменной х.
16. Тип 16 № 5089 
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(1) = 5;
F(2) = 5;
F(n) = 5*F(n − 1) − 4*F(n − 2) при n 2.
Чему равно значение функции F(13)? В ответе запишите только натуральное число.
17. Тип 17 № 56545 
Файл содержит последовательность целых чисел, по модулю не превышающих 10 000. Назовём парой два идущих подряд элемента последовательности.
Задание 17
Определите количество пар, для которых выполняются следующие условия:
— запись элементов пары заканчивается одной и той же цифрой;
— ровно один элемент из пары делится без остатка на 7;
— сумма квадратов элементов пары не превышает квадрат наименьшего из элементов последовательности, запись которых заканчивается цифрой 7.
В ответе запишите два числа: сначала количество найденных пар, затем максимальную величину суммы квадратов элементов этих пар.
Ответ: 

18. Тип 18 № 56518 
Робот стоит в левом верхнем углу прямоугольного поля, в каждой клетке которого записано целое положительное число. За один ход робот может переместиться на одну клетку вправо, вниз или по диагонали вправо вниз.
На каждый шаг вправо робот затрачивает 15 единиц энергии, на шаг вниз — 20 единиц, на шаг по диагонали — 10 единиц. В каждой клетке, включая начальную и конечную, робот пополняет запас энергии на величину, равную записанному в этой клетке числу. В начальный момент (до подзарядки в начальной клетке) запас энергии робота равен нулю.
Необходимо перевести робота в правый нижний угол поля. Определите максимальное и минимальное значения запаса энергии, который может быть у робота после завершения маршрута и подзарядки в последней клетке.
В ответе запишите два числа: сначала максимально возможное значение, затем минимально возможное.
Исходные данные записаны в электронной таблице. Пример входных данных (для таблицы размером 4 × 4):
Задание 18
| 43 | 47 | 25 | 35 |
| 49 | 52 | 83 | 64 |
| 97 | 8 | 22 | 32 |
| 36 | 7 | 85 | 74 |
При указанных входных данных максимальное значение 303 получится при движении по маршруту 43 → 49 → 52 → 83 → 22 → 85 →R 9; 74, а минимальное значение 141 при движении по маршруту 43 → 49 → 8 → 22 → 74. В ответе в данном случае надо записать числа 303 и 141.
Ответ: 

19. Тип 19 № 28236 
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или возвести количество камней в квадрат. Например, имея кучу из 7 камней, за один ход можно получить кучу из 8 или 49 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится 100 или более. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 100 или больше камней.
В начальный момент в куче было S камней, 1
Говорят, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
20. Тип 20 № 28237 
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или возвести количество камней в квадрат. Например, имея кучу из 7 камней, за один ход можно получить кучу из 8 или 49 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится 100 или более. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 100 или больше камней.
В начальный момент в куче было S камней; 1 S
Говорят, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
21. Тип 21 № 28238 
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или возвести количество камней в квадрат. Например, имея кучу из 7 камней, за один ход можно получить кучу из 8 или 49 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится 100 или более. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 100 или больше камней.
В начальный момент в куче было S камней, 1 S
Говорят, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока - значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Найдите минимальное значение S, при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22. Тип 22 № 47606 
В файле 22_25.xlsx содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы — время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) | ID процесса(ов) A |
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1;2 |
| 4 | 7 | 3 |
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 — через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
23. Тип 23 № 7466 
Исполнитель Май4 преобразует число, записанное на экране. У исполнителя три команды, которым присвоены номера:
1. Прибавь 1.
2. Прибавь 2.
3. Прибавь 4.
Первая из них увеличивает число на экране на 1, вторая увеличивает это число на 2, а третья — на 4. Программа для исполнителя Май4 — это последовательность команд. Сколько есть программ, которые число 21 преобразуют в число 30?
24. Тип 24 № 69932 
Найти подпоследовательность максимальной длины, которая имеет арифметический смысл и содержит только цифры 6, 7, 8, 0 и знаки операций «−», «*». При этом должны выполняться следующие условия:
Возле цифры 0 не может быть знака операции.
В выражении не должно быть умножения на отрицательные числа.
В выражении не должно быть повторяющихся знаков операций, таких как «**».
Пример правильного выражения: 6787-86.
Пример неправильного выражения: 6786*−78 (содержит повторяющиеся знаки операции и отрицательное число).
Задание 24
25. Тип 25 № 56553 
Маска числа — это последовательность цифр, в которой могут встречаться специальные символы «?» и «*». Символ «?» означает ровно одну произвольную цифру, символ «*» означает произвольную (в том числе пустую) последовательность цифр.
Пример. Маске 123*4?5 соответствуют числа 123405 и 12376415.
Найдите все натуральные числа, не превышающие 1010, которые соответствуют маске 1?2655*8 и при этом без остатка делятся на 4173.
В ответе запишите все найденные числа в порядке возрастания.
Ответ:







26. Тип 26 № 70553 
Во время сессии студенты сдают 4 экзамена, за каждый из которых можно получить от 2 до 5 баллов. Студенты, получившие хотя бы одну «двойку», считаются не сдавшими сессию. Результаты сессии публикуются в виде рейтингового списка, в котором сначала указаны идентификационные номера студентов (ID), сдавших сессию, в порядке убывания среднего балла за сессию, а в случае равенства средних баллов – в порядке возрастания ID.
Затем располагаются ID студентов, не сдавших сессию: сначала — получивших одну «двойку», затем — две «двойки», потом ID студентов с тремя «двойками» и, наконец, ID студентов, получивших по 2 балла за каждый из экзаменов. Если студенты имеют одинаковое количество «двоек», то их ID в рейтинге располагаются в порядке возрастания.
Повышенную стипендию получают студенты, занявшие в рейтинговом списке первые 25% мест, при условии отсутствия у них «двоек».
Гарантируется, что без «двоек» сессию сдали не менее 25% студентов.
Найдите ID студента, который занимает последнее место среди студентов с повышенной стипендией, а также ID первого в рейтинговом списке студента, который имеет более двух «двоек».
В ответе запишите два целых положительных числа: сначала ID студента, который занимает последнее место среди студентов с повышенной стипендией, затем ID первого в рейтинговом списке студента, который имеет более двух «двоек».
Входные данные.
Задание 24
В первой строке входного файла находится число N, обозначающее количество студентов (целое положительное число, не превышающее 10 000). Каждая из следующих N строк содержит 5 чисел через пробел: ID студента (целое положительное число, не превышающее 100 000) и четыре оценки, полученные им за сессию. Гарантируется, что общее число студентов N кратно 4 и хотя бы один студент имеет более двух «двоек».
Во входном файле все ID различны.
Выходные данные.
Два натуральных числа: искомые ID студентов в порядке, указанном в условии задачи.
Типовой пример организации данных во входном файле:
8
4 4 4 4 4
7 5 5 5 2
10 3 4 4 5
1 4 4 4 3
6 3 5 5 3
2 2 2 2 2
13 2 2 2 3
3 3 3 3 3
При таких исходных данных рейтинговый список ID имеет вид: 4 6 10 1 3 7 13 2. Ответ: 6 13.
Ответ:


27. Тип 27 № 70554 
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд — это набор звёзд (точек) на графике, лежащий внутри прямоугольника высотой H и шириной W. Каждая звезда обязательно принадлежит только одному из кластеров.
Истинный центр кластера, или центроид, — это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Под расстоянием понимается расстояние Евклида между двумя точками A(x1, y1) и B(x2, y2) на плоскости, которое вычисляется по формуле:
В файле A хранятся данные о звёздах двух кластеров, где H = 3, W = 3 для каждого кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата x, затем координата y. Значения даны в условных единицах. Известно, что количество звёзд не превышает 1000.
В файле Б хранятся данные о звёздах трёх кластеров, где H = 3, W = 3 для каждого кластера. Известно, что количество звёзд не превышает 10 000.
Структура хранения информации о звездах в файле Б аналогична файлу А.
Файл A
Файл B
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: Px — среднее арифметическое абсцисс центров кластеров, и Py — среднее арифметическое ординат центров кластеров.
В ответе запишите четыре числа: в первой строке сначала целую часть произведения Px × 10 000 , затем целую часть произведения Py × 10 000 для файла А, во второй строке — аналогичные данные для файла Б.
Возможные данные одного из файлов иллюстрированы графиком.
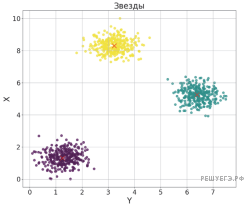
Ответ:



































