Экстремум функции

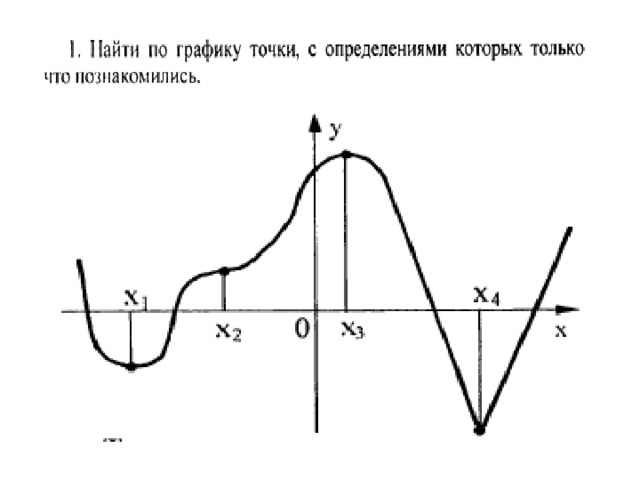
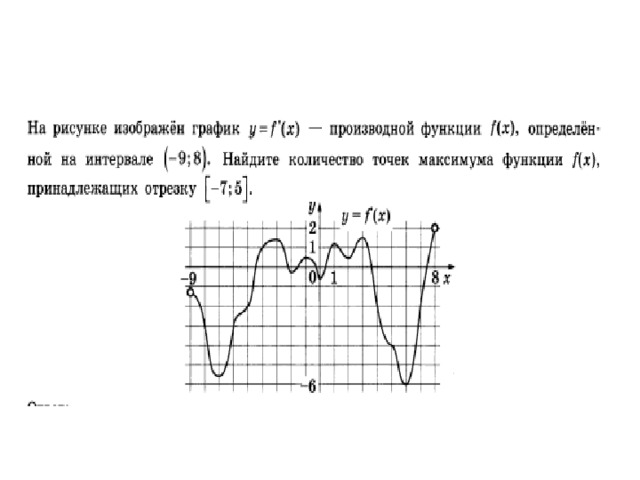
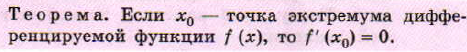Тема: «Экстремумы функции»

Скажи мне, и я забуду.
Покажи мне, и я запомню.
Вовлеки меня, и я научусь.
Китайская мудрость.

Цели урока:

Образовательные:

1. Опираясь на знания учащихся по производной функции помочь сформулировать и осознать определение понятий критических, стационарных точек и точек экстремума; подвести к гипотезе: необходимое и достаточное условие существования экстремума функции.

2. Создать условие для первичного закрепления учащимися умения аналитически и графически определять наличие у функции критических, стационарных точек и точек экстремума.

3. Подготовить учащихся к сдаче ЕГЭ.

Развивающие:

Способствовать развитию учебно-познавательной деятельности, логического мышления.

Воспитательные:

1. Сформировать умения наблюдать, подмечать закономерности, обобщать, проводить рассуждения по аналогии.

2. Развивать мышление, внимание, речь учащегося.

3. Сформировать обще трудовые умения в условиях наибольшей ответственности и ограниченности во времени.

4. Воспитывать умение прислушиваться к другому мнению и отстаивать свою точку зрения.

Тип урока: урок ознакомления с новым материалом.

Ход урока:

I. Организационный момент (Метод информационно-сообщающий)

1. Актуализация знаний. «Мозговой штурм»

1.Вычислить производную функции: ( задание выполняется самостоятельно, с дальнейшей самопроверкой, количество правильных заданий отмечают в листе самоконтроля)

2. Решить неравенство: ( у доски)

3.Определить промежутки монотонности функции : ( у доски два ученика)

А) f(x) = 3х – 9 ( 1 балл)

Б) f(x) = х² + 6х – 9 ( 2 балла)

II. Исследовательская работа. (на миллиметровой бумаге)

Постройте график функции : у = х² –6х + 8;

Ответьте на вопросы :

1. Назовите промежутки возрастания и убывания полученного графика.

2. Назовите точку минимума функции.

3. Как ведет себя производная вблизи этой точки, при переходе через эту точку? А в самой этой точке?

IV. Выдвижение гипотезы (Частично поисковый (эвристический метод))

Сформулируйте гипотезу.

( учащиеся выдвигают гипотезу)

Если производная меняет знак с «-» на «+», а в самой точке равна 0, то данная точка будет точкой минимума функции . ( за выдвижение гипотезы – 4 балла)

Постройте график функции : у = - х² + 4х – 3.

Ответьте на вопросы :

1. Назовите промежутки возрастания и убывания полученного графика.

2. Назовите точку максимума функции.

3. Как ведет себя производная вблизи этой точки, при переходе через эту точку? А в самой этой точке?

Сформулируйте гипотезу.

Работа с учебником.

Стр. 265 – 266. Найти в тексте сформулированную вами гипотезу.

Прочтите её.

Точки минимума и точки максимума называются точками экстремума.

Чем мы будем заниматься на сегодняшнем уроке?

( учиться находить точки экстремума функции )

Какая тема нашего урока?

Экстремумы функции. Записали тему урока.

Сообщение ученицы (метод стимулирования учебной деятельности школьников)

Выдвинутую вами гипотезу доказал французский математик Пьер Ферма 4 века назад.

( историческая справка)

Пьер Ферма (1601-1665) — французский математик, один из создателей аналитической геометрии и теории чисел (теоремы Ферма). Труды по теории вероятностей, исчислению бесконечно малых и оптике (принцип Ферма).

Пьер Ферма открыл методы нахождения экстремумов и касательных, которые, с современной точки зрения, сводятся к отысканию производной.

( учащиеся читают формулировку теорему)

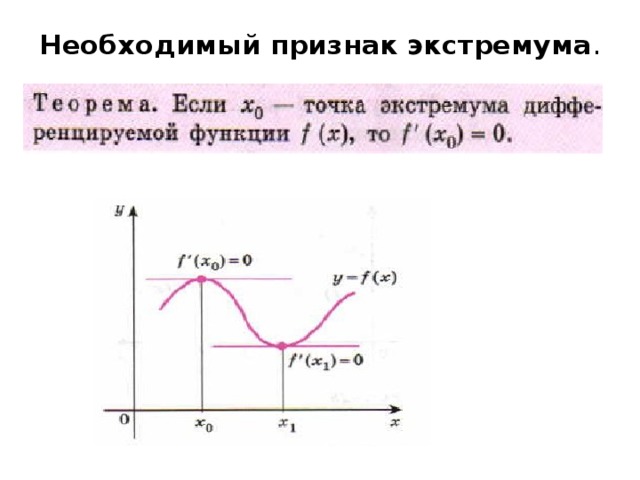
Необходимый признак экстремума.

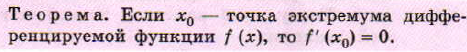
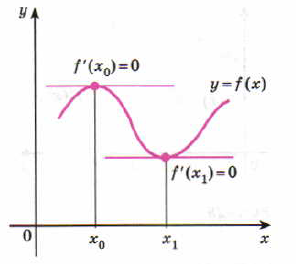
Работа с книгой стр. 267

Найти какие точки называются стационарными, критическими.

( Точки, в которых производная функции равна нулю, называют стационарными

Точки, в которых функция имеет производную, равную нулю, или недифференцируема , называют критическими точками этой функции )

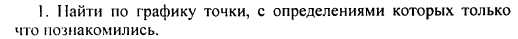
Работа с сигнальными карточками.

Если утверждение верно – «да», если нет – « нет» ( игра «ДА, НЕТ»

За правильный ответ 1 балл

Стр. 268 теорема. ( учащиеся её зачитывают и дают пояснения, как они её понимают)

Достаточный признак экстремума.

У доски: за правильное выполнение – 5 баллов.

Составить алгоритм нахождения точек экстремума функции.

1. Найти область определения функции.

2. Найти f'(x).

3. Найти критические  точки, т.е. точки, где  f'(x) = 0 или f'(x) не существует.
(Производная равна 0 в нулях числителя, производная не существует в нулях знаменателя)

4. Расположить область определения и эти точки на координатной прямой.

5. Определить знаки производной на    каждом из интервалов

6. Применить признаки.

7. Записать ответ.

(Практический метод)

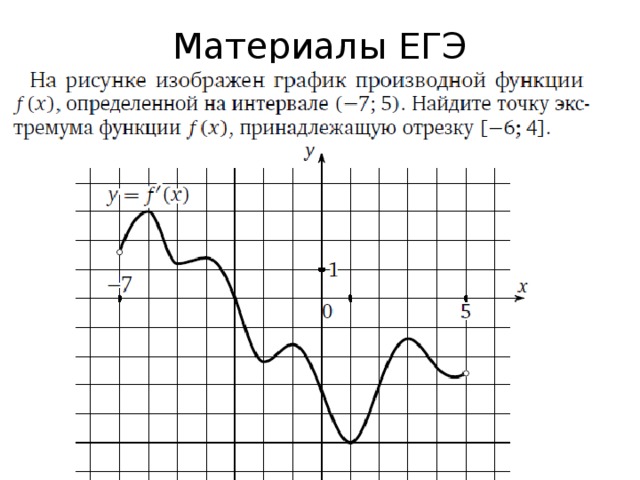
Работа с материалами ЕГЭ

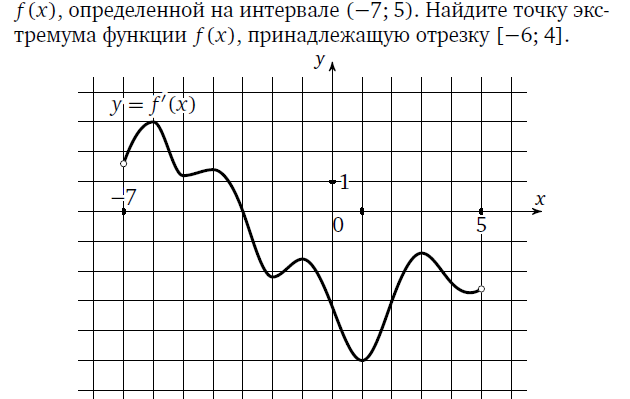
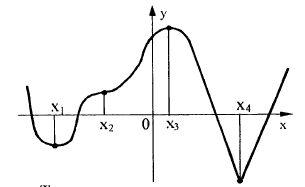
Функция y = f(x) определена на промежутке (-4; 5). На рисунке изображён график её производной. Найдите точку минимума функции y = f(x)

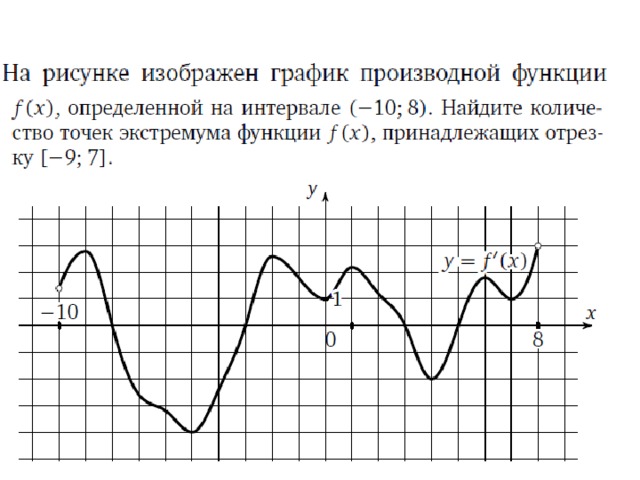
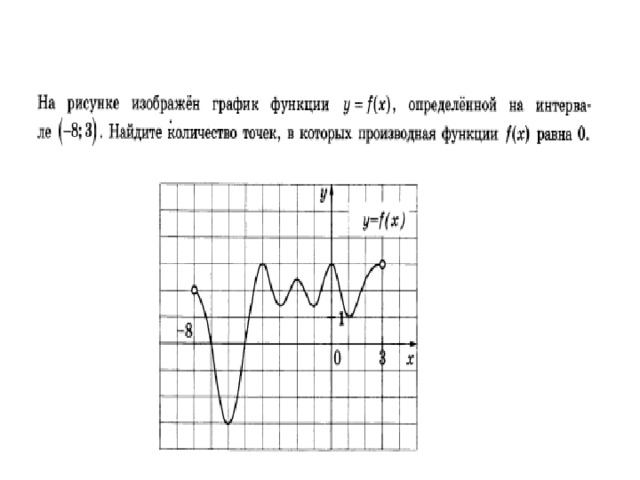
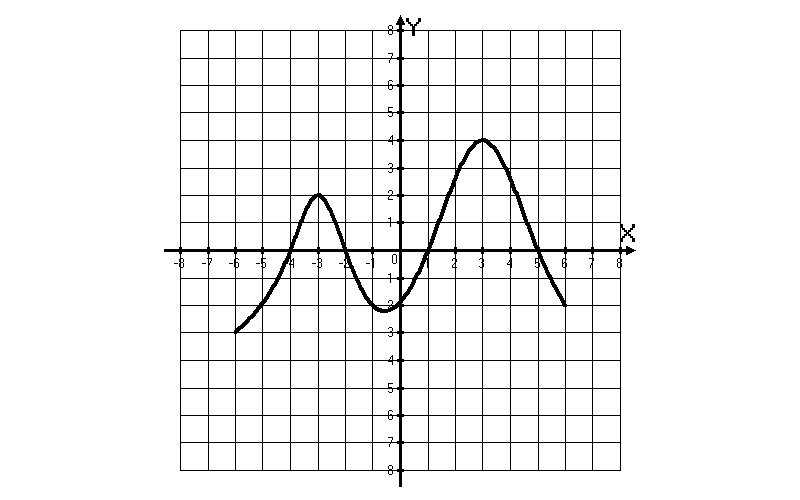
Функция y = f(x) определена на промежутке (- 6; 6). На рисунке изображён график её производной. Найдите точки, в которых производная функции равна нулю (Ответ: х = - 4; х = - 2; х = 1; х = 5).

Итог урока : выставление оценок ( по листам самоконтроля)

д/з: п. 50, № 912 ( 2,4), 913(2,4), 914( 2,4)

• рефлексия учащихся

Я умею …

Я знаю …

Хотелось бы лучше научиться …

Мне нравится …

Мне не нравится …

На уроке я чувствовала себя …

С домашней работой я …

“Великий философ Конфуций однажды сказал: “Три пути ведут к знанию: путь размышления - это путь самый благородный, путь подражания - это путь самый легкий и путь опыта - это путь самый горький”. Выполняя домашнее задание, каждый из вас пройдёт свой путь к знанию.

Скажи мне, и я забуду. Покажи мне, и я запомню. Вовлеки меня, и я научусь.

Китайская мудрость.

№

Задание

1

Ответ

f(x) = 3х 2 – 4 х + 5

2

f(x) = sin x – cos x

3

f(x) = e x + ln x

4

f(x) = е 2х - 6е х + 7

5

f(x) = - х 3 + 3х 2 + 9 х - 29

6х - 4

cоs x + sin x

2e 2x – 6 e x

-3 x 2 + 6 x + 9

Постройте график функции : у = х 2 –6х + 8;

Ответьте на вопросы :

• Назовите промежутки возрастания и убывания полученного графика.
• Назовите точку минимума функции.
• Как ведет себя производная вблизи окрестности этой точки, при переходе через эту точку? А в самой этой точке?

Сформулируйте гипотезу .

Постройте график функции : у = - х 2 + 4х – 3.

• Ответьте на вопросы :
• Назовите промежутки возрастания и убывания полученного графика.
• Назовите точку максимума функции.
• Как ведет себя производная вблизи этой точки, при переходе через эту точку? А в самой этой точке?

Постройте график функции : у = - х 2 + 4х – 3.

Ответьте на вопросы :

• Назовите промежутки возрастания и убывания полученного графика.
• Назовите точку максимума функции.
• Как ведет себя производная вблизи окрестности этой точки, при переходе через эту точку? А в самой этой точке?

Пьер Ферма (1601-1665) — французский математик, один из создателей аналитической геометрии и теории чисел (теоремы Ферма). Труды по теории вероятностей, исчислению бесконечно малых и оптике (принцип Ферма).

Пьер Ферма открыл методы нахождения экстремумов и касательных, которые, с современной точки зрения, сводятся к отысканию производной.

Необходимый признак экстремума .

Алгоритм нахождения точек экстремума функции

1. Найти область определения функции.

2. Найти f'( x ).

3. Найти критические  точки, т.е. точки, где  f'( x ) = 0 или f'( x ) не существует. (Производная равна 0 в нулях числителя, производная не существует в нулях знаменателя)

4. Расположить область определения и эти точки на координатной прямой.

5. Определить знаки производной на    каждом из интервалов

6. Применить признаки.

7. Записать ответ.

д/з: п. 50, № 912 ( 2,4),

913(2,4), 914( 2,4 )

• Я умею …
• Я знаю …
• Хотелось бы лучше научиться …
• Мне нравится …
• Мне не нравится …
• На уроке я чувствовала себя …
• С домашней работой я …

Великий философ Конфуций однажды сказал: “Три пути ведут к знанию: путь размышления - это путь самый благородный, путь подражания - это путь самый легкий и путь опыта - это путь самый горький”. Выполняя домашнее задание, каждый из вас пройдёт свой путь к знанию.

• Конфуций, Кун-цзы (родился приблизительно 551 - умер 479 до н. э.), древнекитайский мыслитель, основатель конфуцианства.

Материалы ЕГЭ