Элементы, множества и графы

&

Элементы и множества. Графы.

Основоположник дискретной математики

• Георг Кантор - великий немецкий ученый, математик. Родился 3 марта 1845 года в России.
• Георг Кантор известен как создатель "теории множеств»

ГЕОРГ КАНТОР

Дискретная математика

• Область математики, занимающаяся изучением свойств структур конечного характера, которые возникают как внутри математики, так и в её приложениях.

• Дискретная (конечная) математика – это раздел математики, не связанный с понятиями предела, непрерывности и бесконечности.

Множество

• Множество можно представить себе как совокупность объектов, обладающих общим свойством.

• Объекты, из которых составлено множество, называются его элементами .

Обозначение множеств

• Множества обычно обозначают большими латинскими буквами (например, A, S, D), а их элементы  - строчными (например, a, s, d).

• Если элемент х принадлежит множеству А, то это обозначается: х€ А; в противном случае говорят, что элемент не принадлежит множеству, это обозначается: х€А.

Способы задания множеств

• 1.     Перечисление элементов: P={точка, прямая, плоскость, тело}, S={0,1,2}.

• 2.     Задание характеристического свойства: L={n|n N и n

Конечность множеств

Множество, содержащее конечное число элементов, называется конечным .

Например, конечным является множество однозначных натуральных чисел {1, 2, 3, 4, 5, 6, 7, 8, 9}.

Множество, не являющееся конечным, называется бесконечным .

Счетность множеств

Бесконечное множество, эквивалентное множеству натуральных чисел N , называется счетным.

Говорят, что все элементы счетного множества можно пронумеровать. В противном случае бесконечное множество будет несчетным.

Основные операции над множествами

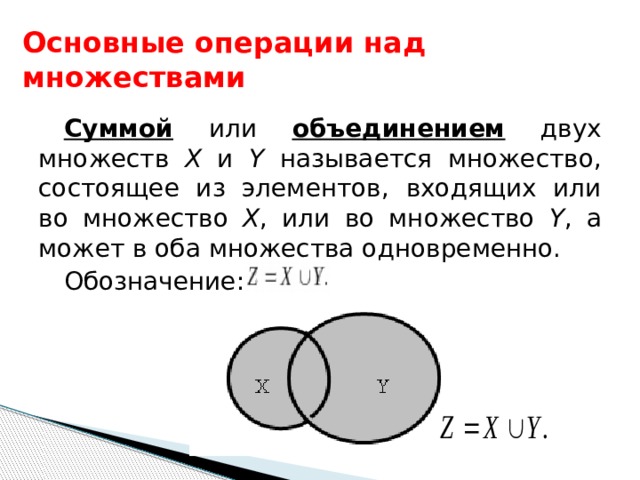
Суммой или объединением двух множеств Х и Y называется множество, состоящее из элементов, входящих или во множество Х , или во множество Y , а может в оба множества одновременно.

Обозначение:

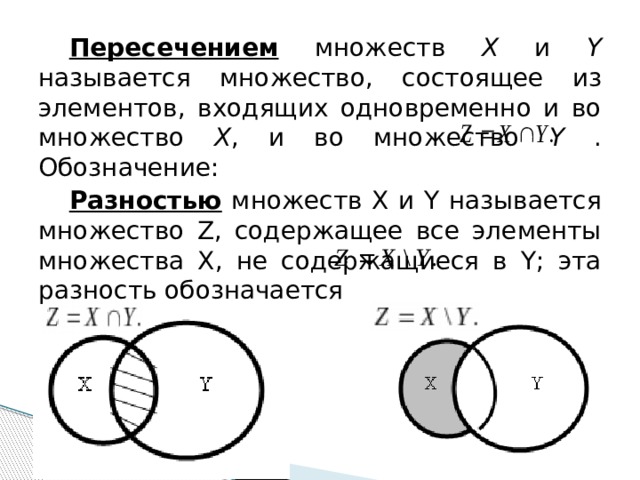
Пересечением множеств Х и Y называется множество, состоящее из элементов, входящих одновременно и во множество Х , и во множество Y . Обозначение:

Разностью множеств X и Y называется множество Z, содержащее все элементы множества X, не содержащиеся в Y; эта разность обозначается

Основные понятия и определения графа и его элементов

.

• Впервые понятие «граф» ввел в 1936 г. венгерский математик Денни Кёниг.

Денни Кенинг

• Но первая работа по теории графов принадлежала перу великого Леонарда Эйлера и была написана еще в 1736 г.

Леонард Эйлер

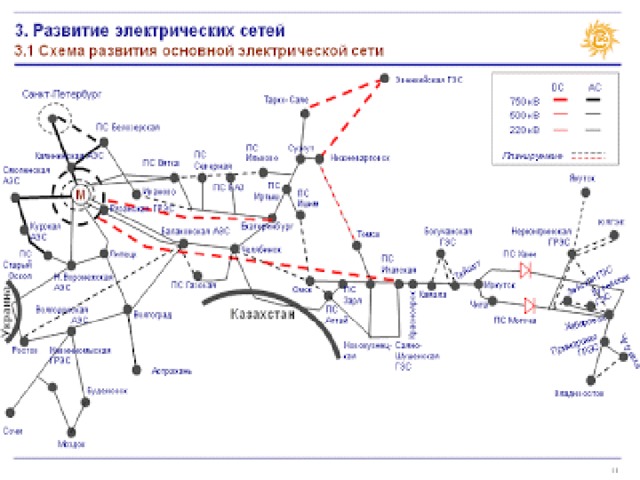
С помощью графов изображаются схемы :

-различных дорог,

-линии воздушных сообщений,

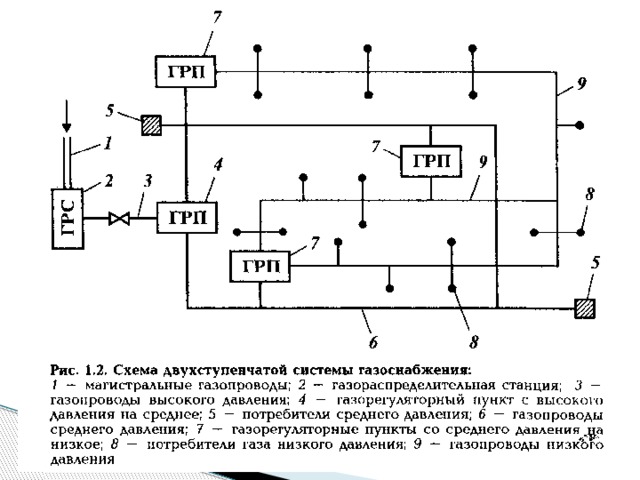
-газопроводов,

-теплотрасс,

-электросетей,

-микросхемы,

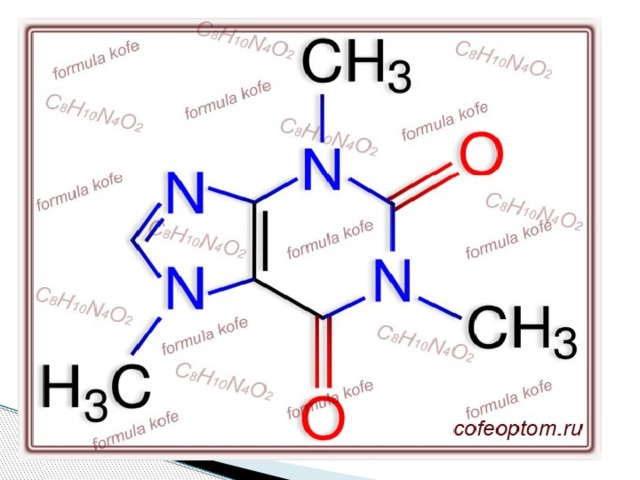
-химические структурные формулы

-и др.

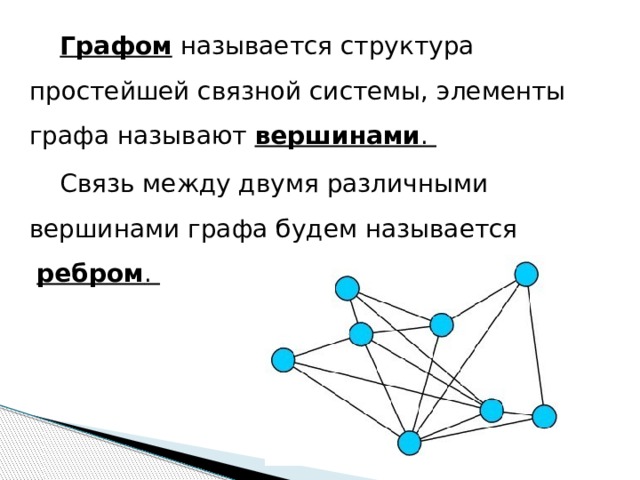
Графом  называется структура простейшей связной системы, элементы графа называют вершинами .

Связь между двумя различными вершинами графа будем называется   ребром .

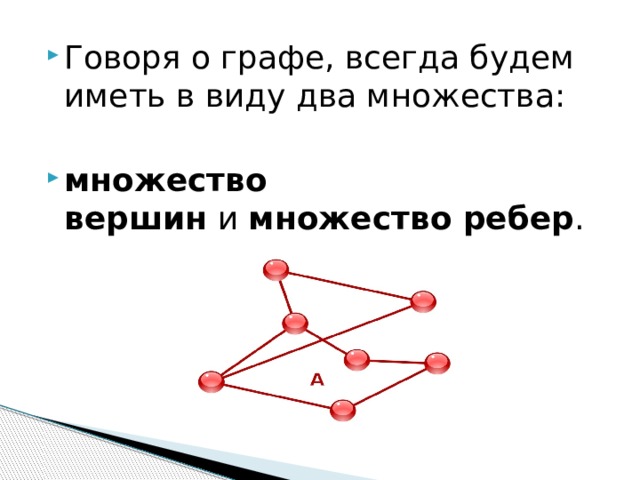
• Говоря о графе, всегда будем иметь в виду два множества:

• множество вершин  и  множество ребер .

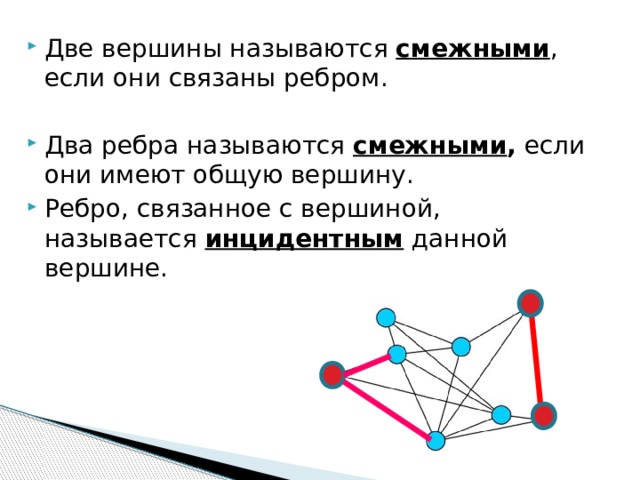
• Две вершины называются смежными , если они связаны ребром.

• Два ребра называются смежными , если они имеют общую вершину.
• Ребро, связанное с вершиной, называется  инцидентным  данной вершине.

Степень вершины графа

• Число ребер инцидентных данной вершине называется её  степенью .

• Степень вершины  vi  обычно обозначают как  degvi

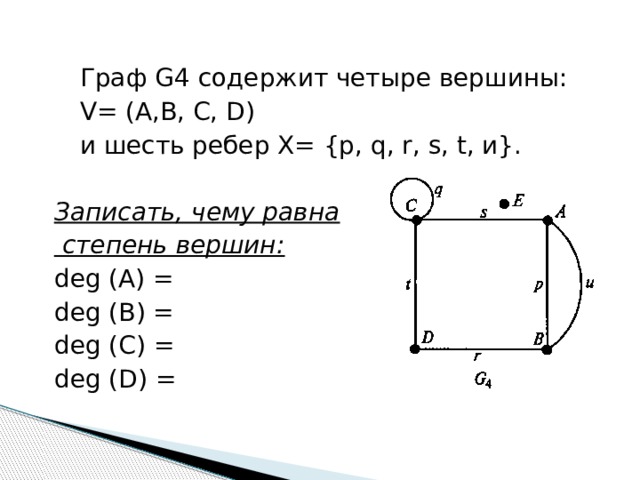
Граф G4 содержит четыре вершины:

V= (A,В, С, D)

и шесть ребер Х= {р, q, r, s, t, и}.

Записать, чему равна

степень вершин:

deg (A) =

deg (В) =

deg (С) =

deg (D) =

Простой граф

• Граф, у которого нет петель и между любыми двумя вершинами не более одной связи называется простым графом

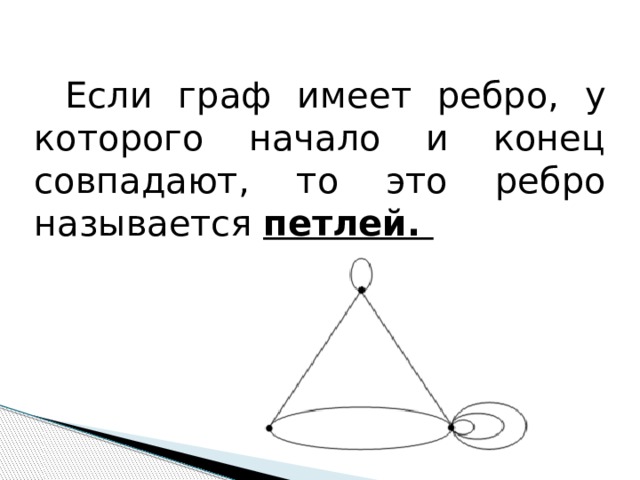
Если граф имеет ребро, у которого начало и конец совпадают, то это ребро называется петлей.

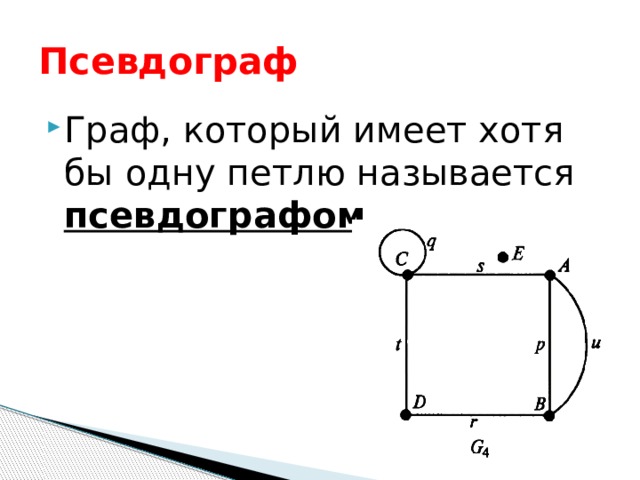
Псевдограф

• Граф, который имеет хотя бы одну петлю называется псевдографом

Мультиграф

• Граф, у которого между двумя вершинами существует более одной связи называется мультиграфом

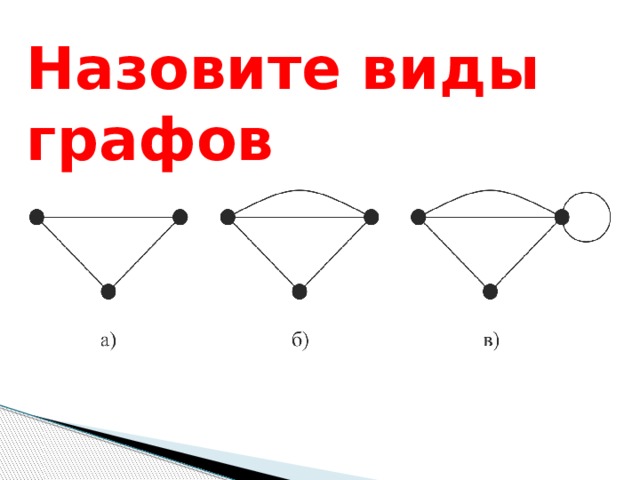
Назовите виды графов

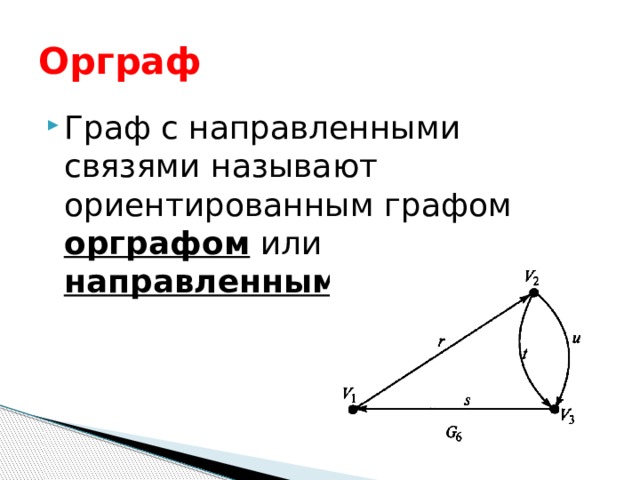
Орграф

• Граф с направленными связями называют ориентированным графом орграфом или направленным.

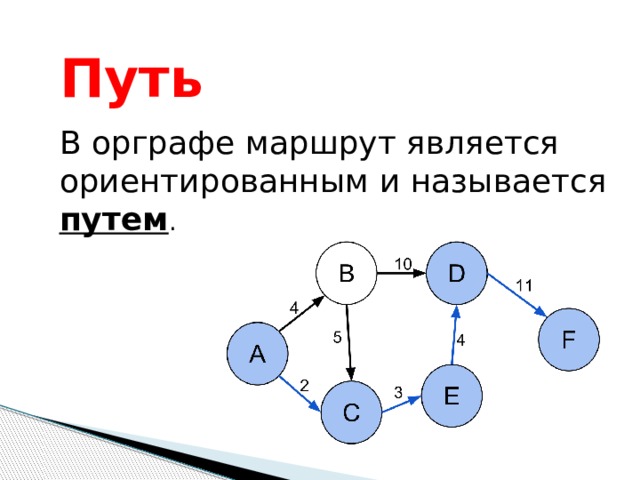
Путь

В орграфе маршрут является ориентированным и называется путем .

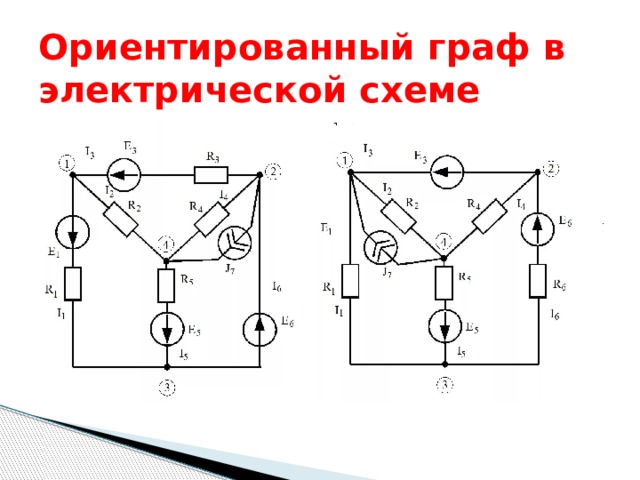
Ориентированный граф в электрической схеме

Задача о Кёнигсбергских мостах

• Обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку

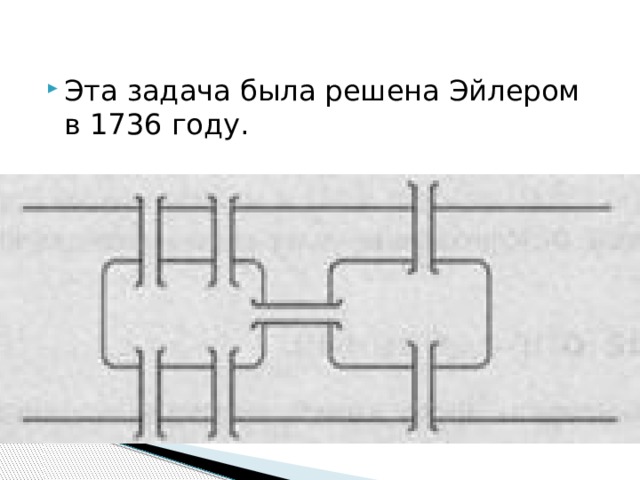
• Эта задача была решена Эйлером в 1736 году.

Эйлеров граф

• Эйлеров путь  в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу.

• Эйлеров цикл  — это эйлеров путь, являющийся циклом.

Условия существования Эйлерова графа

• Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.

• Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.

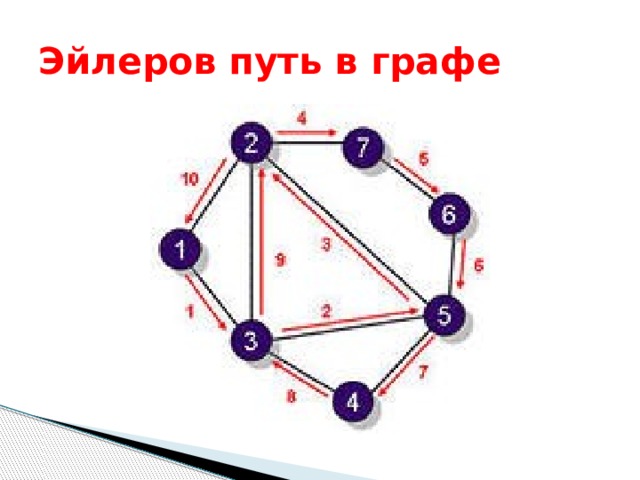
Эйлеров путь в графе

Цепи

• Последовательность смежных вершин, описывающая связь первой и  k-ой вершины, включающая и сами эти вершины называется  простой цепью.

• При этом связываемые вершины (первая и k-ая) называются  концевыми

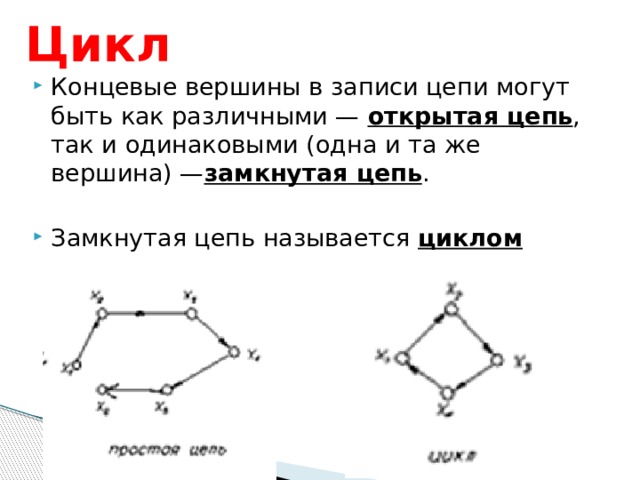
Цикл

• Концевые вершины в записи цепи могут быть как различными —  открытая цепь , так и одинаковыми (одна и та же вершина) — замкнутая цепь .

• Замкнутая цепь называется  циклом

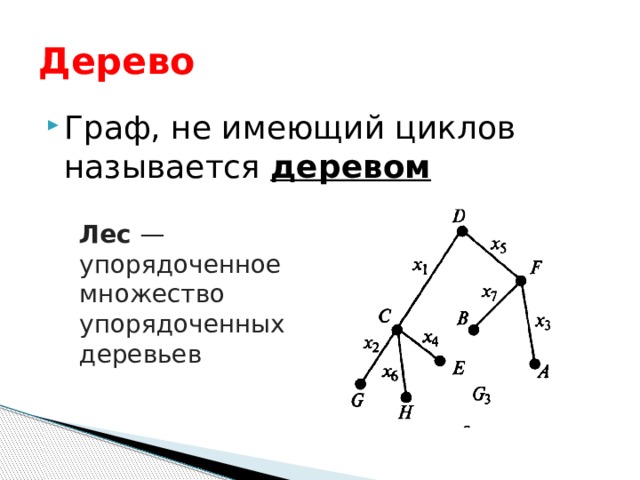
Дерево

• Граф, не имеющий циклов называется деревом

Лес  — упорядоченное множество упорядоченных деревьев

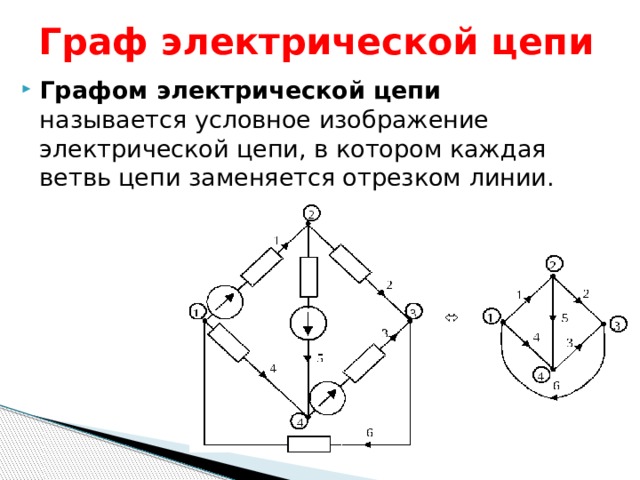
Граф электрической цепи

• Графом электрической цепи называется условное изображение электрической цепи, в котором каждая ветвь цепи заменяется отрезком линии.

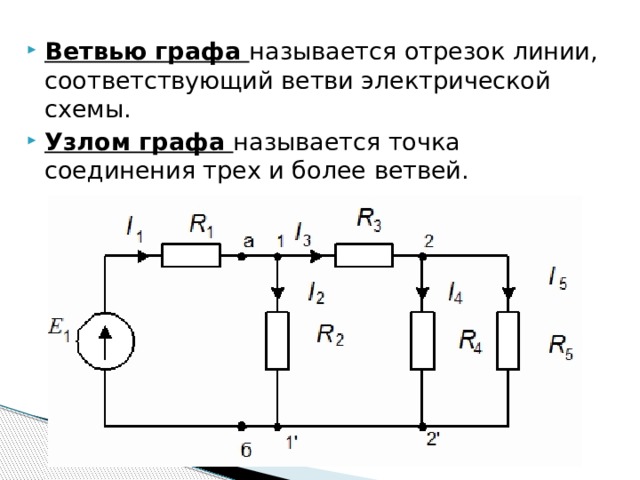
• Ветвью графа называется отрезок линии, соответствующий ветви электрической схемы.
• Узлом графа называется точка соединения трех и более ветвей.

Контрольные вопросы

1) Что такое множество?

2) Что такое граф?

3) Как посчитать степень вершины графа?

4) Опишите виды графов.

4) Что такое Эйлеров граф?

5) Каковы условия существования Эйлерова графа?

6) Что значит граф электрической цепи?