"Фигурные числа"

Содержание

‌‌1. Введение________________________________________________ - 3

2. Основная часть___________________________________________

2.1. История возникновения фигурных чисел_________________ - 4

2.2. Фигурные числа у пифагорейцев________________________ - 5

2.3. Многоугольные числа ________________________________ - 7

2.4. Пространственные фигурные числа______________________ - 9

3. Заключение_______________________________________________ -11

4.Литература________________________________________________ -12

Введение

В мире нет места для

некрасивой математики.

Г. Харди

Многоугольные, или, как их часто называют, фигурные числа были известны ещё в глубокой древности. Они использовались ещё в V – IV веках до н. э. Большой интерес к фигурным числам проявляли индейские математики. Древнегреческие математики предпочитали думать о числах, как о геометрических величинах.

Когда я впервые услышала о фигурных числах, в моём представлении встали красивые числа. Каждая цифра как бы была составлена из геометрических фигур (треугольник, круг, квадрат и т. д.). Но это оказалось не так. Учитель дала нам задание узнать о них больше. Меня это заинтересовало, поэтому я решила глубже познакомиться с ними.

Фигурные числа – общее название чисел, связанных с той или иной геометрической фигурой. Различают следующие виды чисел:

Линейные числа (т. е. простые числа)– числа, которые делятся только на единицу и на самих себя и, следовательно, представимы в виде последовательности точек, выстроенных в линию.

Плоские числа – числа, представимые в виде произведения двух сомножителей.

Телесные числа – числа, выражаемые произведением трёх сомножителей.

Мнение о математике как науке сухой и мертвой живо в обществе и среди учеников по сей день. Одной из основных причин сравнительно плохой успеваемости по математике – слабый интерес многих учащихся к этому предмету. Поэтому в настоящее время большое внимание необходимо уделять формированию познавательного интереса к математике.

Изучение элементов теории фигурных чисел на занятиях по математике в старших классах средней школы не только возможно, но и крайне желательно: обширный исторический материал, расцвеченный увлекательными легендами и мифами, способствует повышению интереса к предмету, общей арифметической культуры школьников.

Поэтому изучение фигурных чисел считаю актуальным.

Целью работы является знакомство с основными теоретико – числовыми доказательствами фигурных чисел.

В соответствии с поставленной целью решались следующие задачи:

- изучить историю происхождения фигурных чисел;

- рассмотреть виды фигурных чисел;

- рассмотреть плоские и пространственные фигурные числа.

Методы исследования:

- обработка и анализ научных источников;

- анализ научной литературы и пособий по исследуемой проблеме.

Собранный мною материал может быть использован как на уроках математики, так и на элективных курсах и курсах по выбору, а также во внеурочной деятельности при проведении мероприятий, научно-практических конференций, исследований, в докладах учащихся.

Основная часть.

2.1 История возникновения фигурных чисел.

Давным – давно, помогая себе при счёте камушками, люди обращали внимание на правильные фигуры, которые можно выложить из камушков. Можно просто класть камушки в ряд: один, два, три. Если класть их в два ряда, чтобы получались прямоугольники, мы обнаружим, что получаются все чётные числа. Можно выкладывать камни в три ряда: получатся числа, делящиеся на три. Всякое число, которое на что–нибудь делится, можно представить таким прямоугольником, и только простые числа не могут быть «прямоугольными».

Фигурные числа были известны ещё в глубокой древности. Предполагают, что впервые они появились в школе Пифагора. Числа древними греками, а вместе с ним Пифагором и пифагорейцами мыслились зримо, в виде камешков, расположенных на песке или на счётной доске – абаке. По этой причине греки не знали нуля, т. к. его невозможно было «увидеть». Но и единица ещё не была полноправным числом, а представлялась как некий «числовой атом», из которого образовывались все числа. Пифагорейцы называли единицу «границей между числом и частями», т. е. между целыми числами и дробями, но в то же время видели в ней «семя и вечный корень». Число же определялось как множество, составленное из единиц. Особое положение единицы как «числового атома», роднило её с точкой, считавшейся «геометрическим атомом». Вот почему Аристотель писал: «Точка есть единица, имеющая положение, единица есть точка без положения». Таким образом, пифагорейские числа в современной терминологии – это натуральные числа.

Числа – камешки раскладывались в виде правильных геометрических фигур. Эти фигуры классифицировались. Так возникли числа, сегодня именуемые фигурными.

Фигурные числа, по мнению пифагорейцев, играют важную роль в структуре мироздания. О них много говорится в пифагорейских учебниках арифметики, созданных Никомахом Геразским и Теоном Смирнским. Изучением фигурных чисел занимались многие математики античности: Эратосфен, Гипсикл и другие. Диофант Александрийский написал большое исследование о свойствах многоугольных чисел, фрагменты которого дошли до наших дней.

Счёт на камушках оставил глубокий след в истории математики. Древние греки, когда им приходилось умножать числа, рисовали прямоугольники; результатом умножения трёх на пять был прямоугольник со сторонами три и пять. Это – развитие счёта на камушках. Множество закономерностей, возникающих при действиях с числами, были обнаружены древнегреческими учёными при изучении чертежей. И долгие века лучшим подтверждением справедливости таких соотношений считался способ геометрический, с прямоугольниками, квадратами, пирамидами и кубами. Даже в ХVII веке, когда была уже хорошо развита алгебра с обозначениями величин буквами, со знаками действий, многие считали её варварской наукой, пригодных для низменных целей – бытовых расчётов, вспомогательных вычислений, но никак не для благородных научных трудов. Один из крупнейших математиков того времени Бонавентура Кавальери, пользовался алгеброй, ибо вычислять с её помощью проще, но для обоснования своих научных результатов все алгебраические выкладки заменял рассуждениями с геометрическими фигурами.

В дальнейшем многие математики интересовались этими числами. Про них доказано много важных и трудных теорем. В Новое время фигурными числами занимались Ферма, Эйлер, Лагранж, Гаусс и другие. Ферма сформулировал в 1670 году так называемую «золотую теорему»:

* Всякое натуральное число – либо треугольное, либо сумма двух или трёх треугольных чисел;

* Всякое натуральное число – либо квадратное, либо сумма двух, трёх или четырёх квадратных чисел;

* Всякое натуральное число – либо пятиугольное, либо сумма от двух до пяти пятиугольных чисел;

* и т. д.

Этой теоремой занимались многие выдающиеся математики, полное доказательство сумел дать Коши в 1813 году.

2.2 Фигурные числа у пифагорейцев.

Фигуры из камешков использовались для представления отдельных чисел в теоретических исследованиях пифагорейцев. Такие визуальные представления позволяли наглядно выявить некоторые свойства чисел.

Квадратными, например, называли числа вида n ∙ n, а прямоугольными – числа

вида (n + 1) ∙ n для некоторого натурального n. Таким образом, 4 = 2 ∙ 2 будет квадратным числом, а 12 = 4 ∙ 3 – прямоугольным.

Для пифагорейцев подобные визуальные представления чисел были важны, в частности потому, что позволяли очень наглядно установить связь между двумя их фундаментальными парами противоположностей: между противоположностью «нечет – чет» с одной стороны и противоположностью «квадрат – прямоугольник» с другой стороны.

Действительно, имеют место следующие элементарные математические факты, которые можно доказать методом математической индукции. Например:

1. Для любого натурального числа n сумма первых n нечётных чисел равняется квадратному числу n ∙ n:

1 + 3 + 5 + … + (2 n - 1) = n².

Доказательство.

а) Проверим при n = 1, 2 ∙ 1 – 1 = 1²; 1 = 1.

б) Предположим, что это верно при n = k,

1 + 3 + 5 + … + (2k - 1) = k².

в ) Докажем, что это верно и при n = k + 1.

1 + 3 + 5 + … + (2k – 1) + (2 ∙ (k + 1) – 1) = k²;

k² +2k + 2 – 1 = k² + 2k +1 = (k + 1)², ч. т. д.

2. Для любого натурального числа n сумма первых n чётных чисел равняется прямоугольному числу (n + 1) ∙ n:

2 + 4 + 6 + … + 2n = (n + 1) ∙ n.

Доказательство.

а) Проверим при n = 1, 2 ∙ 1 = (1 +1) ∙ 1; 2 = 2.

б) Предположим, что это верно при n = k,

2 + 4 + 6 + … 2k = (k + 1) ∙ k.

в ) Докажем, что это верно и при n = k + 1.

2 + 4 + 6 + … + 2k + 2 (k + 1) = (k + 1)(k + 2);

k (k +1) +2k +2 = k² + k +2 k +2 = (k² + k) +(2 k +2) =

= k ∙ (k +1) +2 ∙ (k + 1) = (k + 1) (k + 2), ч. т. д.

Однако пифагорейцы им не пользовались, а заменяли шаги доказательства самоочевидными визуальными построениями, ведущую роль в которых играло понятие гномона. Гномоном (точнее квадратным гномоном) они именовали фигуру, получаемую при операции образования большего квадратного числа из меньшего. Добавляемые при этой операции квадратики в совокупности образуют фигуру, называемую «квадратным гномоном».

Легко заметить, что последовательные квадратные гномоны соответствуют последовательности нечетных чисел, больших единицы (каждый гномон составлен из нечетного числа квадратов):

Таким образом, нечетные числа, большие единицы, визуально представлялись квадратными гномонами.

Описанную выше операцию получения большего квадратного числа из меньшего интерпретировали еще как операцию приложения к меньшему числу соответствующего гномона. Таким образом, любое квадратное число оказывалось возможным породить из единицы посредством последовательного приложения к ней соответствующих квадратных гномонов. В этом и заключалось чисто визуальное доказательство того, что каждое квадратное число является суммой некоторого начального отрезка ряда нечетных чисел.

Совершенно аналогично, прямоугольным гномоном пифагорейцы именовали фигуру, получаемую при операции образования большего прямоугольного числа из меньшего. Добавляемые при этой операции квадратики в совокупности образуют фигуру, называемую «прямоугольным гномоном». Легко заметить, что последовательные прямоугольные гномоны соответствуют последовательности четных чисел, больших двойки (каждый гномон составлен из четного числа квадратов). Таким образом, четные числа, большие двойки, визуально представлялись прямоугольными гномонами. Описанную выше операцию получения большего прямоугольного числа из меньшего интерпретировали еще как операцию приложения к меньшему числу соответствующего гномона. Таким образом, любое прямоугольное число оказывалось возможным породить из двойки посредством последовательного приложения к ней соответствующих прямоугольных гномонов. В этом и заключалось чисто визуальное доказательство того, что каждое прямоугольное число является суммой некоторого начального отрезка ряда четных чисел. Ассоциируя квадраты с квадратными числами, а прямоугольники — с прямоугольными, пифагорейцы утверждали, что квадрат состоит из нечета, а прямоугольник — из чета.

Это утверждение можно сделать особенно наглядным, если раскрасить различными цветами отдельные гномоны, входящие в фигурные числа. В пифагорейской системе фундаментальных пар противоположностей один член каждой пары считался положительным, добрым, благоприятным, другой же имел противоположную окраску. Пифагорейцы считали квадрат более совершенной фигурой, чем прямоугольник, и поэтому относили его к положительному полюсу (а прямоугольник, соответственно, — к отрицательному). Дальше они рассуждали следующим образом: раз нечетное связано с квадратным, то его тоже следует считать положительным, тогда как четное, связанное с прямоугольным, следует считать отрицательным. Такая оценочная квалификация нечетного и четного играла весьма существенную роль в их философии. Однако гораздо более важным представляется то обстоятельство, что эти мистические числовые спекуляции способствовали, тем не менее, отысканию реальных, объективно существующих отношений между числами, т. е. способствовали становлению арифметики как теоретической науки (в отличие от гораздо более древней логистики). Разумеется, мы должны также принять во внимание, что учение о четном и нечетном вообще являлось основополагающим для пифагорейской математики. Эта теория может рассматриваться как самая первая научная теория (т. е. теория, основанная на дедуктивном методе).

Представление чисел в виде правильных геометрических фигур помогало пифагорейцам находить различные числовые закономерности. Фигурное представление чисел помогало им открывать законы арифметических операций, а также легко переходить к числовой характеристике геометрических объектов – измерению площадей и объёмов. Так, представляя число 10 в двух формах: 5 ∙ 2 = 2 ∙ 5, легко «увидеть» переместительный закон умножения: a ∙ b = b ∙ a. В том же числе 10: (2 + 3) ∙ 2 = 2 ∙ 2 + 3 ∙ 2 = 10 можно «разглядеть» и распределительный закон сложения относительно умножения: (a + b) ∙ c = ac + bc.

Наконец, если «камешки», образующие фигурные числа, мыслить в виде равных по площади квадратиков, то, укладывая их в прямоугольное число ab: автоматически получаем формулу для вычисления площади прямоугольника: S = ab.

2.3.Многоугольные числа.

Многоугольные числа также относятся к фигурным. Выкладывая различные правильные многоугольники, получаются разные классы многоугольных чисел. 1.Рассмотрим треугольные числа. Какой же вид они имеют? Заметим, что

1 = 1
         3 = 1 + 2
         6 = 1 + 2 + 3
       10 = 1 + 2 + 3 + 4
       15 = 1 + 2 + 3 + 4 + 5
       . . .
    Мы увидели некоторую закономерность. Попробую доказать, что эта закономерность сохраняется и дальше. Если n-е треугольное число обозначить через Т_n и считать Т₁ = 1, то получится справедлива следующая формула:

Т_n = 1 + 2 + 3 + ... + n.

    На вид она довольно проста, но для вычислений явно не пригодна. Чтобы придать ей более удобную для вычисления форму, заметим, что в правой части равенства равноудалённые от начала и конца слагаемые в сумме дают одно и то же число, а именно n + 1. Напишем нашу формулу два раза, поменяв во втором случае порядок слагаемых на обратный:

Т_n = 1 + 2 + 3 + … + (n – 2) + (n – 1) + n,

Т_n = n + (n – 1) + (n – 2) + … + 3 + 2 + 1 . Сложим «столбиком», получим

2 Т_n = n (n + 1),

откуда Т_n = 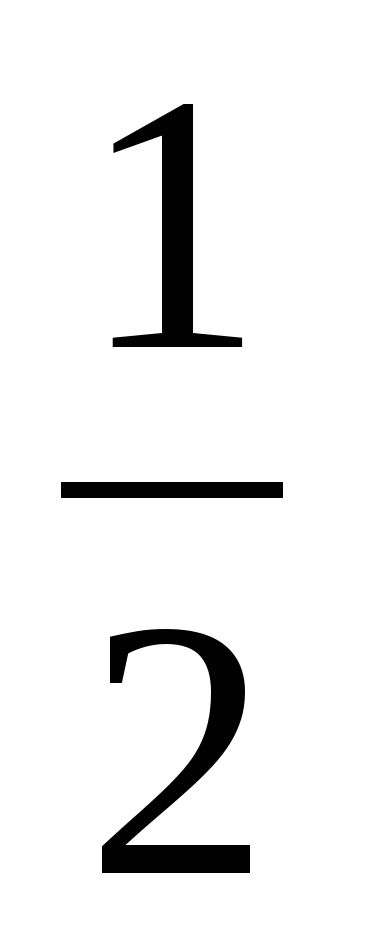n (n + 1).

Применённый здесь метод «спаривания» слагаемых блестяще применил в шестилетнем возрасте мальчик Карл, который впоследствии стал великим Карлом Фридрихом Гауссом, прозванным «королём математики»ещё при жизни.

Кроме треугольных чисел существуют также числа квадратные, пятиугольные, шестиугольные и т. д.

Для каждого числа существуют свои формулы. Квадратные числа связаны таким равенством 1 + 3 + 5 + … + (2 n - 1) = n² , которое было доказано ранее.

2. Чтобы получить выражение для пятиугольных чисел можно применить метод «спаривания» слагаемых, с помощью которого доказывается формула суммы первых n членов арифметической прогрессии

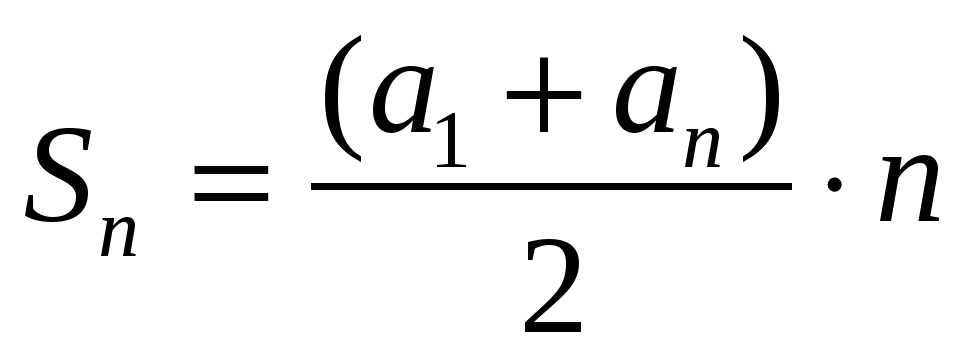или

Я применю формулу суммы первых n членов арифметической прогрессии.

П_n =1+ 4+ 7 + 10 + … + (3n – 2) =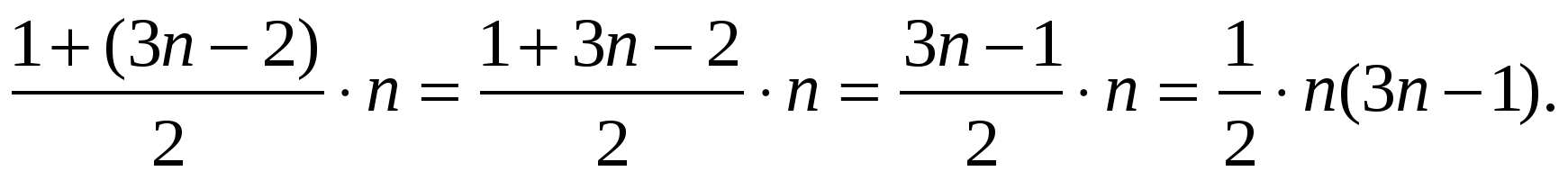

3. Применяя все эти методы можно найти выражения для шестиугольных, семиугольных и т. д. чисел. Выведем общую формулу для любого k-угольного числа.

Пусть 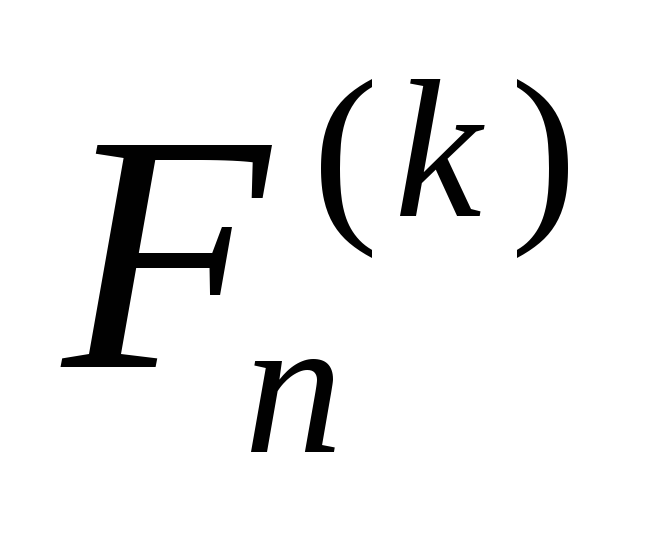обозначает n-е k-угольное число. Рассмотрим k-угольник, порождающий это число. Возьмём одну из вершин этого многоугольника, например, А, и проведём из неё все диагонали. Сколько их будет? Подсчитаем.

Вершину А можно соединить с каждой из остальных (k – 1) вершин; но при соединении А с двумя соседними с ней вершинами мы получим не диагонали, а стороны многоугольника. Значит, диагонали получаются при соединении А

с (k – 1) – 2 = k – 3 вершинами. Это и есть число диагоналей.

Проведя диагонали из вершины А, мы разобьём k-угольник на k – 2 треугольника. Каждый из этих треугольников связан n-м треугольным числом Т_n. Зная же Т_n, мы можем посчитать число точек и в данном k-угольнике, то есть найти формулу для 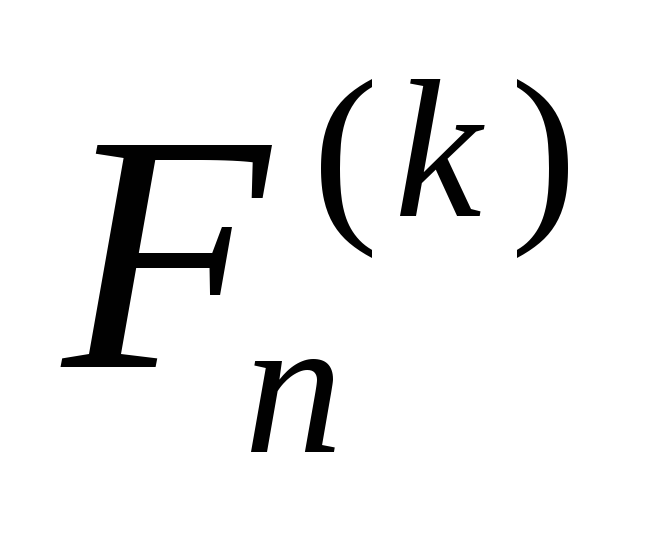. В самом деле, в каждом треугольнике Т_n точек, а треугольников k – 2. Итого –

(k – 2)∙ Т_n точек. При этом точки, лежащие на диагоналях, мы считали два раза – ведь диагональ является общей стороной двух смежных треугольников, а точку А, которая является общей для всех треугольников (k – 2) раза.

Уточним наш подсчёт: на каждой диагонали n точек, а если отбросить точку А, то

n – 1 точка; значит, (n – 1)(k – 3) точек мы считали по два раза; а точку А мы считали

(k – 2) раза и получили при этом на (k – 3) точки больше, чем следовало. Следовательно, из выражения (k – 2)∙ Т_n нужно вычесть число (n – 1)(k – 3) и число

k – 3. это даёт для 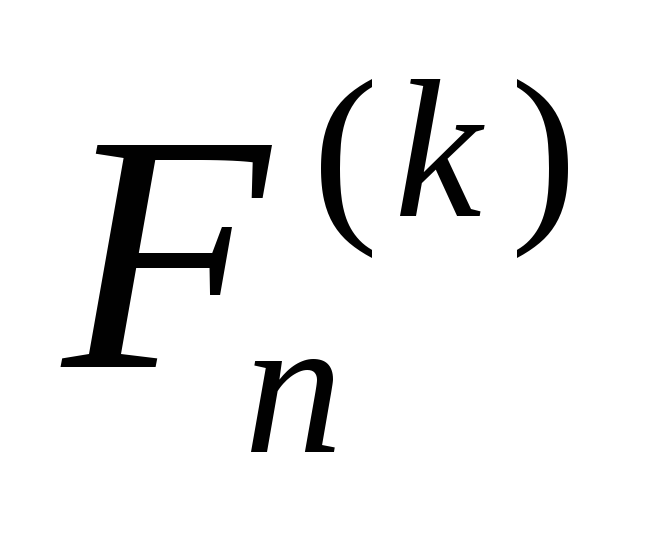следующее выражение:

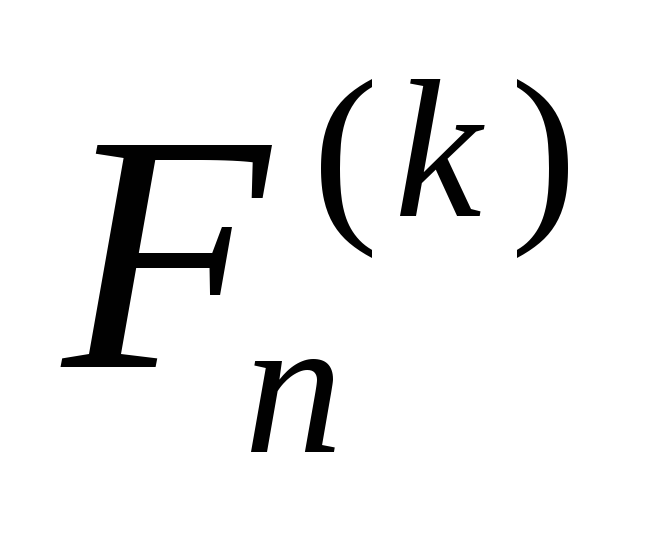= (k – 2)∙ Т_n - (n – 1)(k – 3) - (k – 3). Подставим сюда значение Т_n и проведя элементарные вычисления, получим искомую формулу:

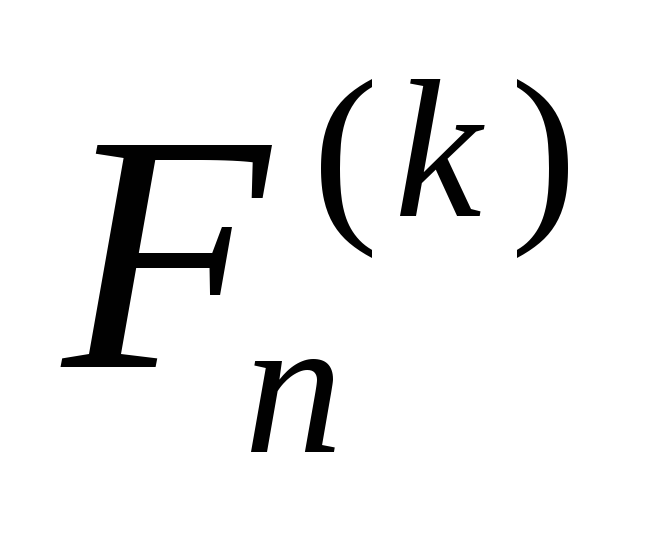= (k – 2)∙ Т_n - (n – 1)(k – 3) - (k – 3) =

= (k – 2)∙ 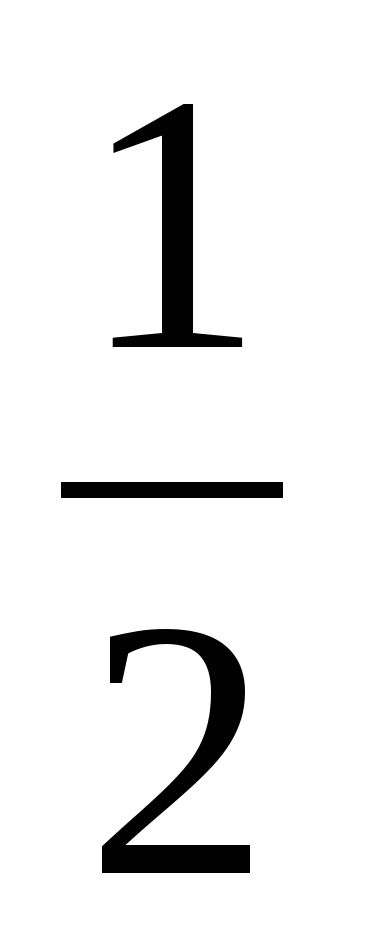n (n + 1) - (n – 1) (k – 3) - (k – 3) =

= (k – 2)∙ 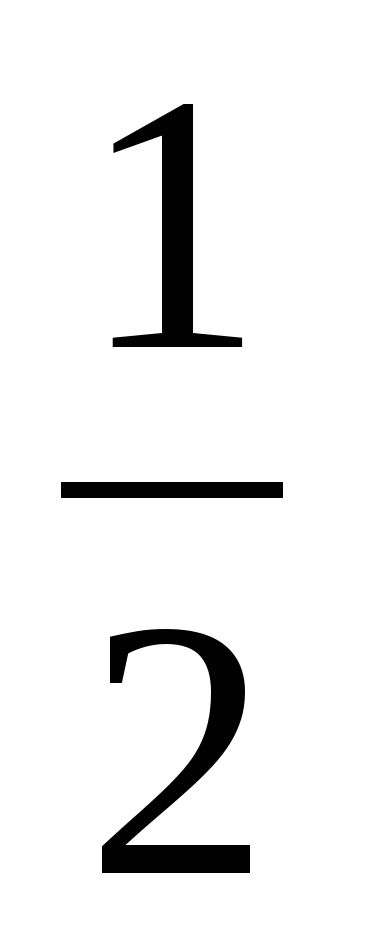n (n + 1) - (k – 3) (n – 1 +1) = 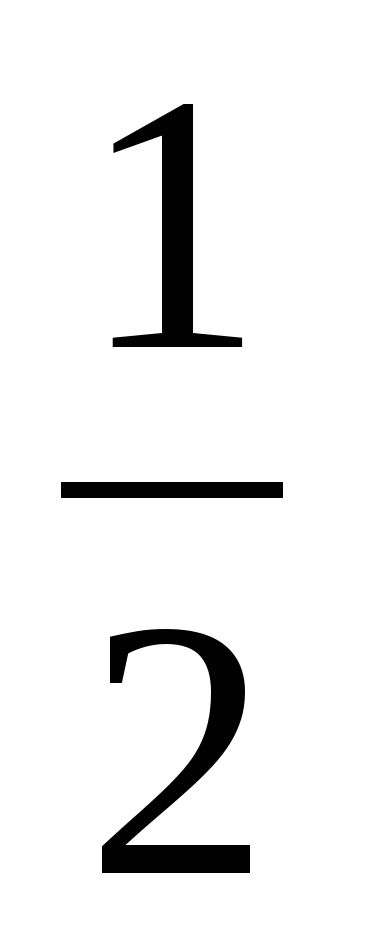(k – 2)∙ n (n + 1) - (k – 3) ∙ n =

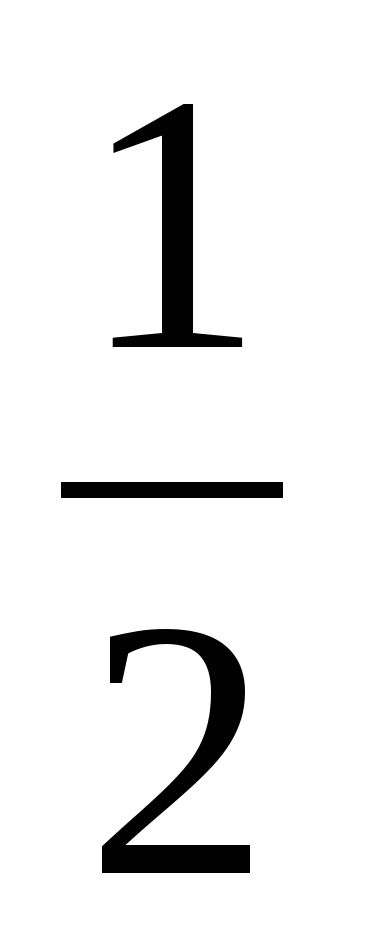= ∙ n [(k – 2)∙ (n + 1) – 2 (k – 3)] = 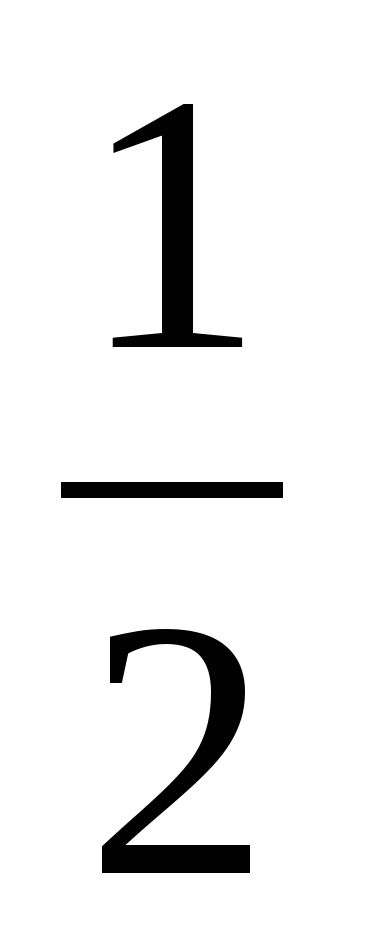∙ n [(k – 2) ∙ n + k – 2 - 2k +6] =

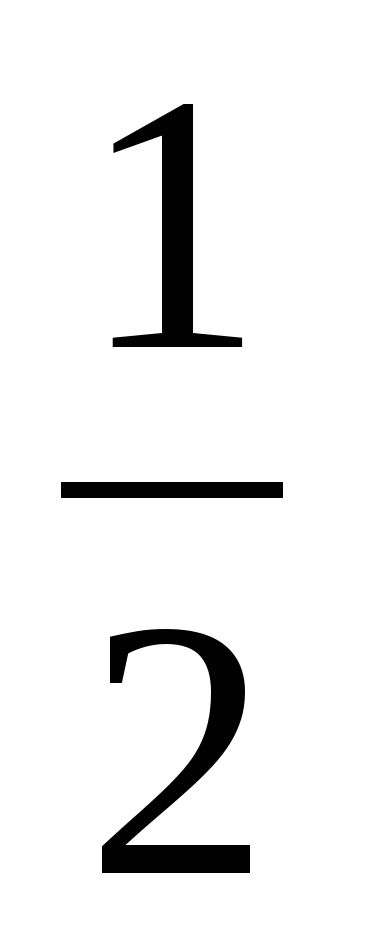= ∙ n [(k – 2) ∙ n + 4 - k] .

Итак, 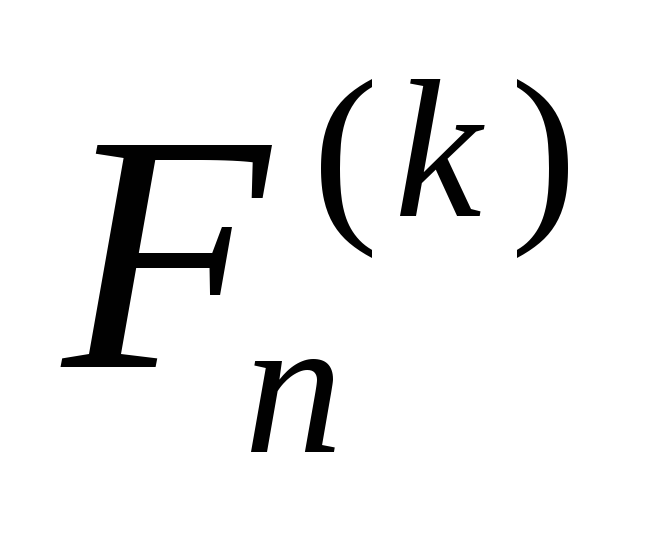= 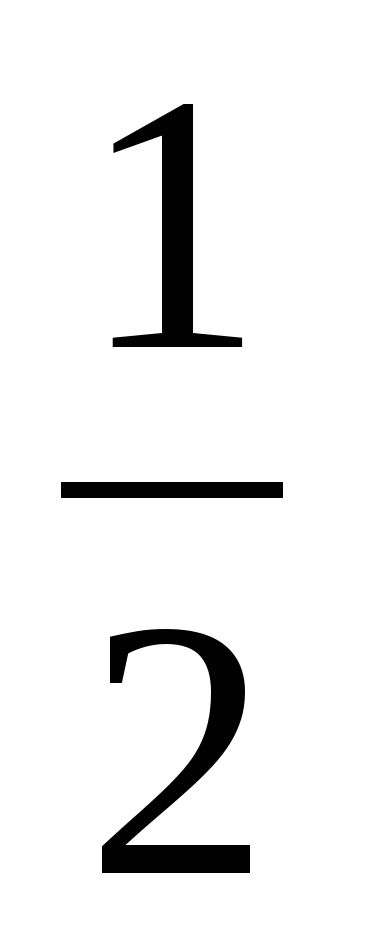∙ n [(k – 2) ∙ n + 4 - k] - общая формула для любого k-угольного числа.

Эту же формулу можно получить, если применить формулу суммы n первых чисел арифметической прогрессии.

Между фигурными числами имеется много интересных зависимостей. Так, например, древнегреческий учёный математик Диофант нашёл простую связь между треугольными числами Т и квадратными К: 8Т + 1 = К.

Можно наглядно представить эту формулу на примере числа 10. На рисунке изображены 81 клеточки, размещённые в квадрате. Они образуют квадратное

число К. Одна клеточка занимает центр квадрата, а остальные 80 сгруппированы в 8 треугольных чисел Т в форме восьми «прямоугольных треугольников». Получается: 8Т + 1 = К.

2.3. Пространственные фигурные числа.

1.Кроме плоских фигурных чисел, существуют ещё пространственные фигурные числа. Пространственные фигурные числа можно получать, составляя последовательные суммы из плоских фигурных чисел

V₁ = S₁,

V₂ = S₁ + S₂,

V₃ = S₁ + S₂ +S₃,

V₄ = S₁ + S₂ + S₃ +S₄ и т. д.

2. Пирамидальные числа возникают при складывании круглых камушков горкой так, чтобы они не раскатывались. Получается пирамида. Каждый слой в такой пирамиде – треугольное число. Наверху один камушек, под ним – 3, под теми – 6 и т. д. Так, ряд треугольных чисел 1, 3, 6, 10, 15 и т. д. производит ряд пирамидальных чисел:

1, 1 + 3 = 4, 1 + 3 + 6 = 10, 1 + 3 + 6 + 10 = 20, …

3.Очень интересны кубические числа, возникающие при складывании кубиков:

1, 2 ∙ 2 ∙ 2 = 8, 3 ∙ 3 ∙ 3 = 27, 4 ∙ 4 ∙ 4 = 64, 5 ∙ 5 ∙ 5 = 125 … и т. д.

Кубические числа представляют собой число точек в кубических таблицах, пирамидальные числа представляют число точек в треугольных пирамидах. Именно от фигурных чисел пошло выражение «Возвести в квадрат или куб». Теперь понятно, почему про такие числа говорят: «два в кубе», «девять в кубе».

Английский математик XVIII в. Э. Варинг поставил задачу о разложении натуральных чисел больших степеней. Было доказано, что всякое натуральное число можно представить в виде суммы не более девяти кубических чисел. В общем случае проблема Варинга остаётся открытой.

Теперь можно понять, почему числа 2 ∙ 2 ∙ 2 ∙ 2= 16, 3 ∙ 3 ∙ 3∙ 3 = 81, 4 ∙ 4 ∙ 4∙ 4 = 256 и т. д. не имеют своего названия. Дело в том, что мы живём в мире трёх измерений (длина, ширина и высота).

Заключение.

В рамках реализации поставленных перед современной системой образования целей и задач на старшей ступени общеобразовательной школы предусматривается профильное обучение, ориентированное на создание условий для качественной дифференциации содержания обучения старшеклассников.

Серьезной проблемой становится в этой ситуации создание соответствующего учебно-методического обеспечения, прежде всего так необходимых сегодня для проведения образовательной реформы учебных пособий, в том числе разработка программ элективных курсов по математике и материалов по их проведению.

Специфика арифметических проблем - простота формулировок, непосредственная связь с элементарной, школьной математикой, глубокие исторические корни в сочетании с богатством, фундаментальностью и разнообразием математического содержания, опирающегося на весь аппарат классической математической науки - позволяет использовать именно теоретико - числовые задачи в качестве одного из наиболее продуктивных источников для построения новых математических курсов для современной школы. В свою очередь, среди арифметических проблем особое место занимают вопросы, связанные с изучением и систематизации свойств тех или иных чисел.

Изучение элементов теории фигурных чисел на занятиях по математике в старших классах средней школы не только возможно, но и крайне желательно: обширный исторический материал, расцвеченный увлекательными легендами и мифами, способствует повышению интереса к предмету; знакомство с основными теоретико - числовыми методами доказательств помогает решению такой важной задачи, как повышение общей арифметической культуры школьников; теснейшие связи курса с алгеброй (арифметическая прогрессия, решение алгебраических уравнений, элементы теории рекуррентных соотношений) способствует углублению базовой математической подготовки; интересные геометрические конструкции выполняют пропедевтическую роль, готовя старшеклассников к изучению современной дискретной математики, в частности теории графов.

Литература.

1. Бендукидзе.А. Д. Физико математический журнал «Квант», 1974 г, № 6.

2. Ван - дер - Варден Б. Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции.

3. Глейзер Г. И. История математики в школе. – М.: Просвещение, 1964.

4. Депман И. Я. История арифметики. Пособие для учителей. – Иэд. Второе. М.: Просвещение, 1965.

5. Диофант. Арифметика и книга о многоугольных числах. – М.: Наука, 1974.

6. Кордемский Б. А. Математическая смекалка. – М.: Наука, 1991.

7. Стиллвелл Д. Математика и её история. – Москва – Ижевск: Институт компьютерных исследований, 2004.

8. Я познаю мир: Детская энциклопедия: Математика. Сост.

А. П. Савин, В. В. Станцо, А. Ю. Котова.

11