Физико- математические софизмы.

Физические софизмы как средство развития рефлексивных и познавательных способностей учащихся

Содержание: I. Ведение. II. Физические софизмы как средство развития рефлексивных и познавательных способностей обучающихся. Сознательное усвоение геометрических теорем; Критическое отношение к выполнению рисунков в геометрических задачах; Нарушение законов равносильности равенства; Нарушение законов равносильности неравенства; Нарушение определения понятия арифметического корня; Приём «преднамеренная ошибка». III. Заключение. IV. Список литературы. I. Ведение. «Школьное дело должно быть нацелено на выработку у подрастающего поколения склонностей и способностей к постоянной рефлексивной работе со знанием, и от успешности школы в решении этой проблемы зависят наши судьбы» Б.М. Бим-Бад. Что же это за рефлексивная работа, от которой зависят наши судьбы? Рефлексия – это анализ, осознание осуществленной деятельности, мышления, общения и психологического состояния в этой деятельности. Именно рефлексия развивает умение использовать свой внутренний потенциал, самосознание. «Выработать» у учащихся «склонность» к рефлексивной работе, значит вооружить их вполне определенными приемами быть не пассивными потребителями знаний, а активными пользователями, ориентированными на осмысление способов познания, анализ, сравнение и перенос знаний. Одним из механизмов развития рефлексивных способностей учащихся является поощрение сомнений и независимой оценки учащимися происходящего. Великий мыслитель древности Сократ утверждал, что нет ни одного положения, которое само по себе было бы настолько понятно, что не стоило бы его исследовать, подвергать сомнению. Для поощрения подвергать все сомнению, анализу и оценке, мы используем математические софизмы. Если в математике путем логической цепи рассуждений, в одном звене которой намеренно допущена трудноуловимая ошибка, хотят убедить кого-то в неверности всем известного математического положения, то перед нами математический софизм. Доказывая математические утверждения, мы постоянно ссылаемся на формулировки теорем, законов, определений. При этом каждая ссылка должна быть точной. Если в определении или законе изменить хотя бы одно слово, смысл утверждения может совершенно измениться. Нередко мы употребляем в рассуждениях слова, точный смысл которых детям не вполне ясен, а поэтому его применение необоснованно. Сократ был первым, кто обратил внимание на значимость точных высказываний. Своими наводящими вопросами, конкретными примерами он побуждал собеседника уточнять определение. Говорят, когда Ксантиппа сообщила родителям, что выходит замуж за Сократа, они спросили, чем занимается жених. И она ответила: «Он учит людей думать!» На уроках математики дети часто получают неверные ответы, хотя, на первый взгляд, применяют верный способ решения. С обидой и возмущением реагируют они на замечания учителя, указавшего на неточности, допущенные в формулировках теорем, определений, понятий, законов. Проблема многих ученических неудач – небрежность в приведенных рассуждениях, выкладках при решении задач. Софистами в древней Греции называли философов-учителей, задачей которых было научить своих учеников «мыслить, говорить и делать». Будучи в большинстве случаев глубоко образованными людьми, они не столько передавали ученикам знания из различных областей греческой науки, столько стремились научить их владеть искусством словесных состязаний. Чтобы выйти победителем в словесном поединке, софисты часто пользовались тем, что противник недостаточно глубоко знает предмет, о котором идет речь, недостаточно внимателен и наблюдателен и поэтому не в состоянии отличить фальшь от правды. II. Математические софизмы как средство развития рефлексивных и познавательных способностей обучающихся. 1. Сознательное усвоение геометрических теорем. В своей учебной деятельности софизмы мы используем как на уроках так и во внеурочное время. Так, на уроках введения нового понятия на этапе вводной части софизмы позволяют создать положительную ауру, эмоциональный настрой на работу, привлечь внимание к рассматриваемой теме. Пример 1. «Катет прямоугольного треугольника равен его гипотенузе». Дан прямоугольный треугольник АВС. DЕ – перпендикуляр к АС в его середине; ВМ – биссектриса угла В; М – точка пересечения указанного перпендикуляра и биссектрисы. Из точки М опущены перпендикуляры МК на ВС и МL на АВ. ВКМ = ВМL. Следовательно, ВК=ВL, (1) п АМD = DМС, АМ = МС СКМ = ALM. Следовательно СК = AL. (2) Складываем равенства (1) и (2): ВК=КС=ВL+AL, Или ВС=АВ, Т.е. катет прямоугольного треугольника равен его гипотенузе. Вывод: Разбор софизма помогает сознательному усвоению признаков равенства прямоугольных треугольников, учащимся 7 классов. Пример 2. «Всякая окружность имеет два центра». Возьмем произвольный угол AВС и в произвольно взятых на сторонах этого произвольного угла точках D и Е построим перпендикуляры к соответствующим сторонам. Пусть М – точка пересечения этих перпендикуляров. Проведем окружность через три точки D¸М и Е. Пусть она пересекает стороны данного угла в точках К и L. Соединим точки К и L с точкой М. Угол КDМ – прямой (по построению); следовательно, будучи вписанным углом, он опирается на диаметр КМ. Угол LЕМ – также прямой и вписанный; следовательно, он также опирается на диаметр LМ. Итак, КМ и LМ – диаметры одной окружности. Середина каждого из них есть центр этой окружность. Окружность имеет два центра. 2. Критическое отношение к выполнению рисунков в геометрических задачах. Пример 3. «Во всякой окружности можно построить хорду, не проходящую через центр, но равную диаметру». Пусть АВ – диаметр (рис.), АС – хорда данной окружности, а F – середина хорды АС. Через точки В и Е проведем хорду ВFD. Точки D и С соединим отрезком прямой. Угол АFВ = углу DFС как вертикальные, Угол А = углу D как вписанные, опирающиеся на одну и ту же дугу ВС; АЕ = FС - по построению. Значит, ∆ АВЕ = ∆ DFС (по стороне и двум углам). Но в равных треугольниках против равных углов лежат равные стороны, следовательно, АВ = DС. (Здесь неправильно применяется теорема о признаке равенства треугольников.) Пример 4. «Прямой угол равен тупому». Возьмем отрезок МN (рисунок) и от его концов отложим два равных отрезка NВ и МА. NВ – перпендикулярен к МN, а МА – не перпендикулярен к МN. Пусть угол АМN будет тупым. 1) Соединим точки А и В отрезком прямой. Очевидно, этот отрезок не параллелен МN. Из середин отрезков АВ и МN точек К и F восставим перпендикуляры к этим прямым. Пусть О – их точка пересечения. Тогда МО = NО и АО = ВО (Точки, лежащие на серединных перпендикулярах, равноудалены от концов данных отрезков). АМ = ВN – по условию. Тогда ∆АОМ - ∆ВОN и угол АМО = углу ВNО. Но угол ОМF = углу ОNF. Поэтому угол АМО + ОМF = углу ВNО + + угол ОNF. Значит, угол АМF = углу ВNF. 2) Если точка пересечения О лежит ниже прямой МN (рисунок), то ∆АМО = ∆ВОN и, следовательно, угол АМО = углу ВNО. Кроме того, угол FМО = углу FNО и угол АМО – угол FМО = углу ВNО – угол FNО. Значит, угол АМF = углу ВNF. Разъяснение. Рассмотрение двух случаев является лишь видимостью общности доказательства, так как его ход зависит не только от положения точки О. Так, в случае 2 (рисунок) тупой угол АМN в сумме с острым углом ОМN может дать угол, превышающий 180° (рисунок), и тогда заключение о равенстве прямого и тупого углов уже сделать нельзя. Таким образом, 2-й случай должен быть разбит еще на два варианта. Первый – уже рассмотрен нами (рисунок), а второй вариант (рисунок) не приводит к результатам, полученным в других случаях. Если теперь рассуждать от противного, то неминуемо придем к выводу, что 2-й вариант 2-го случая является единственно возможным. Вывод: Ошибка в задачах позволяет критически относиться к выполнению рисунков и применяемым теоремам. Пример 5. «Средняя линия любой трапеции равна нулю». РЕШЕНИЕ. Пусть АВСD – произвольная трапеция. АD = а и ВС = b. Докажем, что = 0. Проведем диагонали АС и ВD и на продолжении оснований трапеции отложим отрезки DЕ = b и ВК = а. Соединим точки К и Е. Диагональ ВD разделится на три части: ВМ = x, МF = у, FD = z. Из подобия треугольников DEF и KFB следует, что = или = . Сравнивая пропорции (1) и (2), получим: = = Применяя известное свойство ряда равных отношений (сумма предыдущих так относится к сумме последующих, как один из предыдущих относится к своему последующему), получим: = ; = , а = - 1. Следовательно, = - 1, но = , значит, = - 1 или = - b и = 0, поэтому и = 0. Разъяснение. Свойство ряда равных отношений справедливо, если члены отношений не равны нулю. В данном случае можно показать, что , поэтому = 0. Разбор этих задач развивает наблюдательность и сознательное усвоение темы. Всем известен закон равносильности: обе части равенства можно умножить (разделить) на одно и то же число. Но часто забывают необходимость проверки равенства этого числа нулю. 3. Нарушение законов равносильности равенства. Пример 6. «Отрезки параллельных прямых, заключенные между сторонами угла, равны». Пусть угол АВС – произвольный угол. АС || DЕ (рисунок). Докажем, что АС = DЕ. Из подобия треугольников АВС и DВЕ следует, что = или АВ · ВЕ = ВD · ВС. (1) Умножим обе части равенства на разность АС – DЕ: (АС – DЕ) · АВ · ВЕ = (АС – DЕ) ВD · ВС; АВ · ВЕ · АС – АВ · ВЕ · DЕ = АС · ВD · ВС – DЕ ·ВD · ВС, или АС · АВ · ВЕ – АС · ВD · ВС = АВ · ВЕ · DЕ – DЕ · ВD · ВС, или АС (АВ · ВЕ – ВD · ВС) = DЕ (АВ · ВЕ – ВD · ВС). Разделив обе части равенства на АВ · ВЕ – ВD · ВС, получим АС = DЕ. Разъяснение. Выражение АВ · ВЕ – ВD · ВС равно нулю. Это непосредственно следует из равенства (1). Пример 7. «5 = 7». Доказательство равенства 5 = 7. Пусть число а будет в полтора раза больше числа b, т.е. а = b. Умножая обе части на 4, получим: 4а = 6b, но 4а = 14а – 10а и 6b = 21b - 15b. Тогда 14а – 10а = 21b - 15b, или 15b – 10а = 21b - 14а; 5 (3b – 2а) = 7 (3b – 2а). Разделив обе части на 3b – 2а, будем иметь: 5 = 7 (?). Где ошибка? (выражение 3b – 2а = 0, а делить на 0 нельзя.) Пример 8. «Всякое число во второй степени есть единица». Пусть x = y = Отсюда = Вычтя равенство (2) из равенства (1) по частям, получим x - = y - Или x – y = - = Разложим х – у на множители: · = - Делим обе части последнего равенства на: + = 1 Или 2 = 1, так как х = , то 2 = 1. Или =1. А вот умножение (деление) обеих частей неравенства на одно и то же число (не обратили внимания на знак числа). 4. Нарушение законов равносильности неравенства. Пример 9. «Для любых а и b, таких, что а b, всегда а 2b». Если бы это утверждение было справедливо, то из неравенства 5 4 следовало бы неравенство 5 8. Пусть а b. Умножим обе части этого неравенства на b. Имеем: аb . Отнимем от обеих частей по : аb - - , или а(b – а) (b – а) (b + а). Разделив обе части на (b – а), получим: а b + а. Сложив исходное неравенство с полученным, будем иметь: 2a 2b + а или а 2b, что и требовалось доказать. Разъяснение. Так как а b – по условию, то b – а 0. Поэтому при деление обеих частей неравенства на эту разность необходимо изменить знак неравенства. Нарушение определения арифметического значения квадратного корня из числа приводит к известному софизму 2х2 = сколько вы хотите. 5. Нарушение определения понятия арифметического корня. Пример 10. «2 · 2 = 5» Рассмотрим верное числовое равенство: 16 – 36 = 25 – 45 Прибавим к обеим частям равенства одно и то же число : 16 – 36 + = 25 – 45 + Получилось верное равенство. Представим его в следующем виде: - 2· 4 · + = - 2 · 5 · + Это есть полные квадраты двух выражений: (4 - )² = (5 - )² Извлекая квадратный корень из обеих частей равенства, получим 4 - = 5 - Прибавим к обеим частям равенства по , получим равенство 4 = 5 или 2 · 2 = 5. Пример 11. «а = b. Все числа равны между собой». Рассмотрим верное числовое равенство: – а (а + b) = – b(а + b), где а и b любые числа. Прибавим к обеим частям равенства одно и то же число : - а(а+ b) + = – b(а + b) + Получилось верное равенство. Представим его в следующем виде: - 2· а · + = - 2 · b · + Это есть полные квадраты двух выражений: (а - )² = (b - )² Извлекая квадратный корень из обеих частей равенства, получим а - = b - Прибавим к обеим частям равенства число , получим равенство а = b. Пример 12. «Любое число равно противоположному ему числу». Возьмем любое число а, обозначим его через х, получим равенство х=а. Умножим обе части этого равенства на -4а. -4ах = -4а². К обеим частям равенства прибавим х²: х² - 4ах = х² - 4а². Перенесем -4а² в левую часть равенства с противоположным знаком: х² - 4ах + 4а² = х² или (х – 2а)² = х². Извлечем квадратный корень из обеих частей равенства: х – 2а = х, но х = а, значит, а – 2а = а или –а = а. 6. Приём «преднамеренная ошибка». Изучая софизмы, мы показали обучающимся, какие парадоксы можно получить, если неточно применять теорему или формулу. Но ведь и в определениях каждое слово существенно. Если в определении изменить или опустить хотя бы одно слово, смысл определения может совершенно измениться. Очень важно показать на уроке, к каким парадоксам ведет неточность, допущенная не только в определении, но и в применении математического понятия. В своей работе мы успешно применяем приём «преднамеренная ошибка». Для этого преднамеренно изменим данное в учебнике определение. Пример 1. В определении простого числа опустим слово «только», получится определение: «Натуральное число, большее единицы, называется простым, если оно имеет «….» два натуральных делителя». Согласно этому «новому» определению все натуральные числа являются простыми, так как у каждого числа всегда есть два натуральных делителя. Если в верном определении есть слово-ограничитель «только» два делителя, то по «новому» определению не запрещено иметь и три, и четыре и т.д. делителей. Пример 2. В определении квадратного уравнения опустим утверждение «а 0», получим следующее определение: «Уравнение вида ах + bх + с = 0, где а, b и с любые действительные числа, называется квадратным». Согласно этому определению уравнение 2х – 3 = 0 является квадратным (а = 0; b = 2; с = -3). Пример3. Вспомним определение медианы треугольника: «Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника». Заменим в этом определении слово «отрезок» словом «линия» (такую ошибку в седьмом классе допускают обучающиеся довольно часто). Подумаем, что же изменилось? Нарисуем линию, которая не является отрезком. Увидев такую «медиану», дети больше не станут в этом определении заменять слово «отрезок» словом «линия». В А С М Пример 4. В определении параллелограмма заменим слово «четырехугольник» словом «фигура»: «Фигура, у которой противоположные стороны попарно параллельны, называется параллелограммом». Что же получилось? Нарисуем такую фигуру Это всё - параллелограммы. III. Заключение. «Софизмы – формально кажущееся правильным, но по существу ложное умозаключение, основанное на преднамеренно неправильном подборе исходных положений». «Словарь русского языка» С.И.Ожегов Разбор софизмов на уроках и на внеурочных занятиях развивает критическое мышление, прививает навыки сознательного усвоения изучаемого материала. Обнаружить ошибку в софизме – значит осознать ее, а осознание ошибки предупреждает от повторения ее в других математических рассуждениях. Решение софизмов развивает у обучающихся умение обосновывать свои утверждения, анализировать результат своей мыслительной деятельности. Очень важно добиваться отчетливого понимания допущенной ошибки в софизме, иначе желаемые результаты работы не будут достигнуты. Софизмы можно предлагать обучающимся в качестве готовой задачи, где ребята должны найти ошибку в рассуждении. Этот приём позволяет формировать у обучающихся склонность и способность к рефлексивной работе, но больший интерес вызывает у школьников софизмы, доказанные учеником (желательно неуспешным в математике), которого можно заранее подготовить. Из опыта нашей работы мы видим, что в классах, где использовались указанные механизмы развития рефлексивных способностей, обучающиеся намного реже допускают ошибки в доказательствах, сознательно оценивают результаты своей работы не только на уроках математики, но и на других уроках. Представляем некоторые высказывания о мыслительной деятельности, которые можно использовать на уроках математики: «В математических вопросах нельзя пренебрегать даже самыми малыми ошибками». И. Ньютон «Именно математическое дает надежнейшие правила: кто им следует – тому не опасен обман чувств». Л. Эйлер «Только с алгеброй начинается строгое математическое учение». Н.И. Лобачевский «Величие человека – в его способности мыслить». Б. Паскаль «Правильно понятая ошибка – это путь к открытию» И.П. Павлов IV. Список использованной литературы: 1. Гельфанд М.Б., Павлович В.С. Внеклассная работа по математике. М. 1965. 2. Глейзер Г. И. История математики в школе. М. 1981. 3. Декарт Р. Правила руководства ума. М. 1989. 4. Калягин Ю. М. Учись решать задачи. М. 1980. 5. Колосов А.А. Книга для внеклассного чтения по математике. М. 1963. 6. Перельман Я. И. Занимательная алгебра. М. 1980. 7. Пойа Д. Как решать задачу. М. 1961. 8. Пойа Д. Математика и правдоподобные рассуждения. М.1975. 9. Фридман П. М.

Понятие о софизмах и логических парадоксах

Непреднамеренная ошибка, допущенная человеком в мышле­нии, называется паралогизмом.

Паралогизмы допускают мно­гие люди. Преднамеренная ошибка с целью запутать своего противника и выдать ложное суждение за истинное называется софизмом. Софистами называют людей, которые ложь пыта­ются выдать за истину путем различных ухищрений.

В математике имеются математические софизмы. В кон­це XIX - начале XX в. большой популярностью среди учащих­ся пользовалась книга В. И. Обреимова “Математические софизмы”, в которой собраны многие софизмы. И в ряде совре­менных книг собраны интересные математические софизмы'. Например, Ф. Ф. Нагибин формулирует следующие матема­тические софизмы:

1) “5 = 6”;

2) “2 • 2 = 5”;

3) “2 = 3”;

4) “Все числа равны между собой”;

5) “Любое число равно половине его”;

6) “Отрицательное число равно положительному”;

7) “Любое число равно нулю”;

8) “Из точки на прямую можно опустить два перпендикуляра”;

9) “Прямой угол равен тупому”;

10) “Всякая окружность имеет два центра”;

11) “Длины всех окружностей равны” и многие другие.

2*2=5.

Требуется найти ошибку в следующих рассужде­ниях. Имеем числовое тождество: 4:4=5:5. Вынесем за скобки в каждой части этого тождества общий множитель. Получим 4(1 : 1) = 5(1 : 1). Числа в скобках равны. Поэтому 4 =5, или 2 *2=5.

5 =1.

Желая доказать, что 5 = 1, будем рассуждать так. Из чисел 5 и 1 по отдельности вычтем одно и то же число 3. Полу­чим числа 2 и -2. При возведении в квадрат этих чисел получа­ются равные числа 4 и 4. Значит, должны быть равны и исход­ные числа 5 и 1. Где ошибка?

Понятие о логических парадоксах

Парадокс - это рассуждение, доказывающее как истинность, так и ложность некоторого суждения или (иными словами) до­казывающее как это суждение, так и его отрицание. Парадоксы были известны еще в древности.

Их примерами являются: “Куча”, “Лысый”, “Каталог всех нормальных каталогов”, “Мэр города”, “Генерал и брадобрей” и др. Рассмотрим некоторые из них.

Парадокс “Куча”.

Разница между кучей и не-кучей - не в одной песчинке. Пусть у нас есть куча (например, песка). Начи­наем из нее брать каждый раз по одной песчинке, и куча остает­ся кучей. Продолжаем этот процесс. Если 100 песчинок - куча, то 99 - тоже куча и т. д. 10 песчинок - куча, 9 - куча,... 3 песчин­ки - куча, 2 песчинки - куча, 1 песчинка - куча. Итак, суть пара­докса в том, что постепенные количественные изменения (убав­ление на 1 песчинку) не приводят к качественным изменениям.

Парадокс “Лысый” аналогичен парадоксу “Куча”, т. е. раз­ница между лысым и не-лысым не в одной волосинке.

Парадоксы теории множеств

В письме Готтлобу Фреге от 16 июня 1902 г. Бертран Рассел сообщил о том, что он обнаружил парадокс множества всех нор­мальных множеств (нормальным множеством называется мно­жество, не содержащее себя в качестве элемента).

Примерами таких парадоксов (противоречий) являются “Ка­талог всех нормальных каталогов”, “Мэр города”, “Генерал и брадобрей” и др.

Парадокс, называемый “Мэр города”, состоит в следующем: каждый мэр города живет или в своем городе, или вне его. Был издан приказ о выделении одного специального города, где жили бы только мэры, не живущие в своем городе. Где должен жить мэр этого специального города? а). Если он хочет жить в своем городе, то он не может этого сделать, так как там живут только мэры, не живущие в своем городе, б). Если же он не хочет жить в своем городе, то, как и все мэры, не живущие в своих городах, должен жить в отведенном городе, т. е. в своем. Итак, он не может жить ни в своем городе, ни вне его.

Парадокс “Генерал и брадобрей” состоит в следующем: каж­дый солдат может сам себя брить или бриться у другого солдата. Генерал издал приказ о выделении одного специального солдата-брадобрея, у которого брились бы только те солдаты, которые себя не бреют. У кого должен бриться этот специально выделенный солдат-брадобрей? а). Если он хочет сам себя брить, то он это­го не может сделать, так как он может брить только тех солдат, которые себя не бреют, б). Если он не будет себя брить, то, как и все солдаты, не бреющие себя, он должен бриться только у одного специального солдата-брадобрея, т. е. у себя. Итак, он не может ни брить себя, ни не брить себя.

Этот парадокс аналогичен парадоксу “Мэр города”. Парадокс “Каталог всех нормальных каталогов” получа­ется так. Каталоги подразделяются на два рода:

1) такие, которые в числе перечисляемых каталогов не упо­минают себя (нормальные), и

2) такие, которые сами входят в число перечисляемых ката­логов (не-нормальные).

Библиотекарю дается задание составить каталог всех нор­мальных и только нормальных каталогов. Должен ли он при со­ставлении своего каталога упомянуть и составленный им? Если он упомянет его, то составленный им каталог окажется не-нормальным, т. е. он не может упоминать его. Если же библиотекарь не упомянет свой каталог, то один из нормальных каталогов - тот, который он составил, - окажется неупомянутым, хотя должен был бы быть упомянутым, как все нормальные каталоги. Итак, биб­лиотекарь не может ни упомянуть, ни не упомянуть составляе­мый им каталог. Как же тут быть? Посмотрим на этом примере, как разрешаются подобные парадоксы.

Естественно заметить, что понятие “нормальный каталог” не имеет фиксированного объема, пока не установлено, какие каталоги следует рассматривать (в какой, например, библиоте­ке и в какое время находящиеся). Если будет дано задание со­ставить каталог всех нормальных каталогов на 20 июня 1998 г., то объем понятия “каталог всех нормальных каталогов” будет фиксирован и при составлении своего каталога библиотекарь не должен будет его упоминать. Но если аналогичное задание бу­дет дано уже после того, как каталог составлен, то придется учесть и этот каталог. Так разрешается парадокс.

Таким образом, в логику входит категория времени, категория изменения: приходится рассматривать изменяющиеся объемы понятий. А рассмотрение объема в процессе его изменения – это уже аспект диалектической логики. Трактовка парадоксов мате­матической логики и теории множеств, связанных с нарушением требований диалектической логики, принадлежит С. А. Яновской. В примере с каталогом удается избежать противоречия потому, что объем понятия “каталог всех нормальных каталогов” берет­ся на какое-то определенное, точно фиксированное время, напри­мер, на 20 июня 1998 г. Имеются и другие способы избежать про­тиворечий такого рода.

 

СОДЕРЖАНИЕ.

1.    Введение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

2.    Софизм как понятие. . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

3.    Экскурс в историю. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

4.    Алгебраические софизмы. . . . . . . . . . . . . . . . . . . . . . . .8

5.    Геометрические софизмы . . . . . . . . . . . . . . . . . . . . . . . 11

6.    Арифметические софизмы. . . . . . . . . . . . . . . . . . . . . . . 14

7.    Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

8.    Список литературы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

ВВЕДЕНИЕ.

 

Наверняка, каждый человек хоть раз в жизни слышал подобную фразу: «Дважды два равно пяти» или хотя бы: «Два равно трем». На самом деле, таких примеров можно привести очень много, но что все они обозначают? Кто их выдумал? Имеют ли они какое-нибудь логическое объяснение или же это лишь вымысел???

Именно эти вопросы я хочу рассмотреть в своей работе, название которой - математические софизмы. Неслучайно я выбрала именно математические софизмы (хотя бывают и логические, и словесные). Они, как мне кажется, более интересны, имеют четкое логическое объяснение, кроме того, с математическими софизмами мы встречаемся намного чаще, чем с обычными. Само понятие математических софизмов предполагает несколько видов софизмов, ведь в математические можно включить и алгебраические, и геометрические, и простейшие арифметические.

Глава 1. «Понятие софизма. Исторические сведения»

Понятие софизма.

Софизм - (от греческого sophisma – уловка, ухищрение, выдумка, головоломка), умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям. Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибок.

Что же такое математический софизм? Математический софизм - удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. История математики полна неожиданных и интересных софизмов, разрешение которых порой служило толчком к новым открытиям. Математические софизмы приучают  внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записи чертежей, за законностью математических операций. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если  их не понимать.

Что касается типичных ошибок в софизмах, то они таковы: запрещенные действия, пренебрежение условиями теорем, формул и правил, ошибочный чертеж, опора на ошибочные умозаключения. Нередко, ошибки, допущенные в софизме, настолько умело скрыты, что даже опытный математик не сразу их выявит. Именно в этом и проявляется связь математики и философии в софизмах. На самом деле,  софизм- гибрид не только математики и философии, но и логики с риторикой. Основные создатели софизмов – древнегреческие ученые-философы, но тем не менее, они создавали  математические  софизмы, основываясь на элементарных аксиомах, что еще раз подтверждает связь математики и философии в софизмах. Кроме того, очень важно правильно преподнести софизм, так, чтобы докладчику поверили, а значит, необходимо владеть даром красноречия и убеждения. Группа древнегреческих ученых, начавшая заниматься софизмами как отдельным математическим явлением, назвала себя софистами. Об этом подробнее в следующем разделе.

Экскурс в историю.

  Софистами называли группу древнегреческих философов 4-5 века до н.э., достигших большого искусства в логике. В период падения нравов древнегреческого общества( 5 век) появляются так называемые учителя красноречия, которые целью своей деятельности считали и называли приобретение и распространения мудрости, вследствие чего они именовали себя софистами. Наиболее известна деятельность старших софистов, к которым относят Протагора из Абдеры, Горгия из Леонтип, Гиппия из Элиды и Продика из Кеоса. Но суть деятельности софистов много больше, чем простое обучение искусству красноречия. Они обучали и просвещали древнегреческий народ, старались способствовать достижению нравственности, присутствия духа, способности ума ориентироваться во всяком деле. Но софисты не были учеными. Умение, которое должно было быть достигнуто с их помощью, заключалось в том, что человек учился иметь в виду многообразные точки зрения. Основным направление деятельности софистов стала социально-антропологическая проблема. Они рассматривали самопознание человека, учили сомневаться, но все же, это очень глубокие философские проблемы, которые стали основой для мыслителей Европейской культуры. Что касается самих софизмов, то они стали как бы дополнением к софистике в целом, если рассматривать ее как истинно философское понятие.

            Исторически сложилось, что с понятием софизма связывают идею о намеренной фальсификации, руководствуясь признанием Протагора, что задача софиста- представить наихудший аргумент как наилучший путем хитроумных уловок в речи, в рассуждении, заботясь не об истине, а об успехе в споре или о практической выгоде. Там не менее, в Греции софистами называли и простых ораторов.

         Известнейший ученый и философ Сократ по началу был софистом, активно участвовал в спорах и обсуждениях софистов, но вскоре стал критиковать учение софистов и софистику в целом. Такому же примеру последовали и его ученики (Ксенофонт и Платон). Философия Сократа была основана на том, что мудрость приобретается с общением, в процессе беседы. Учение Сократа было устным. Кроме  того, Сократа и по сей день считают самым мудрым философом.

          Что касается самих софизмов, то, пожалуй, самым популярным на тот момент в Древней Греции был софизм Евбулида : «Что ты не терял, ты имеешь. Рога ты не терял. Значит у тебя рога». Единственная неточность, которую возможно было допустить, то это- двусмысленность высказывания. Данная постановка фразы является нелогичной, но логика возникла намного позже, благодаря Аристотелю, поэтому, если бы фраза строилась так: «Все, что ты не терял. . .», то вывод стал бы логически безупречным.

         Подобных софизмов действительно очень много, но хотелось бы больше всего разобрать некоторые математические софизмы, которые наиболее популярны и известны. Об этом  и будет следующая глава.

Глава 2. «Математические софизмы»

Разбор и решение любого рода математических задач, а в особенности нестандартных, помогает  развивать смекалку и логику. Математические софизмы относятся именно к таким задачам. В этом разделе работы я рассмотрю три типа математических софизмов: алгебраические, геометрические и арифметические.

           Алгебраические софизмы.

1. «Два неодинаковых натуральных числа равны между собой»

 

 

решим систему двух уравнений:   х+2у=6,     (1)

                                                           у=4- х/2    (2)

подстановкой у из 2го ур-я в 1 по-

лучаем х+8-х=6, откуда 8=6

где ошибка???

Уравнение (2) можно записать как  х+2у=8, так что исходная система запишется в виде:

    Х+2у=6,

    

    Х+2у=8

В этой системе уравнений коэффициенты при переменных одинаковы, а правые части не равны между собой, из этого следует, что система несовместна, т.е. не имеет ни одного решения. Графически это означает, что прямые у=3-х/2 и у=4-х/2 параллельны и не совпадают.

Перед тем, Как решать систему линейных уравнений, полезно проанализировать, имеет ли система единственное решение, бесконечно много решений или не имеет решений вообще.

2. «Сочетательное и переместительное свойства алгебраической суммы не имеют места»

 

Рассмотрим сумму бесконечного числа слагаемых, поочередно равных плюс единице и минус единице, т.е.

                       S=1-1+1-1+1-1+1-1+1-1+…….. ,(1)

И попробуем найти значение этой суммы.

 Сначала поступим следующим образом. Будем объединять слагаемые в пары, начиная со второго слагаемого, ставя перед каждой парой «минус», т.е.

                         S=1-(1-1)-(1-1)-….=1-0-0-…=1.

Теперь переставим каждое положительное слагаемое той же суммы (1) на место отрицательного и обратно, тогда

                         S=-1+1-1+1-1+1-…=-1+(1-1)+(1-1)+…=-1+0+0+…=-1.

Итак, по-разному переставляя слагаемые суммы(1), мы пришли к различным значениям этой суммы: 1 и –1, в итоге сумма слагаемых изменяется от перегруппировки слагаемых ,а сочетательное и переместительное свойства алгебраической суммы не имеют места.

Где ошибка?

3. «Дважды два равно пяти».

Обозначим 4=а, 5=b, (a+b)/2=d. Имеем: a+b=2d, a=2d-b, 2d-a=b. перемножим два последних равенства по частям. Получим: 2da-a*a=2db-b*b. Умножим обе части получившегося равенства на –1 и прибавим к результатам d*d. Будем иметь: a ²-2da+d²=b² -2bd+d², или (a-d)(a-d)=(b-d)(b-d), откуда a-d=b-d и a=b, т.е. 2*2=5

Где ошибка???

Из равенства квадратов двух чисел не следует, что сами эти числа равны.

4. «Отрицательное число больше положительного».

 

Возьмем два положительных числа а и с. Сравним два отношения:

                      а        -а

                     -с         с

Они равны, так как каждое из них равно –(а/с). Можно составить пропорцию:

                    а            -а

                   -с              с

Но если в пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего. В нашем случае а-с, следовательно, должно быть –ас, т.е. отрицательное число больше положительного.

Где ошибка???

   Данное свойство пропорции может оказаться неверным, если некоторые члены пропорции отрицательны.

Геометрические софизмы.

1. «Через точку на прямую можно опустить два перпендикуляра»

Попытаемся "доказать", что через точку, лежащую вне прямой, к этой прямой можно провести два перпендикуляра. С этой целью возьмем треугольник АВС. На сторонах АВ и ВС этого треугольника, как на диаметрах, построим полуокружности. Пусть эти полуокружности пересекаются со стороной АС в точках Е и Д. Соединим точки  Е и Д прямыми с точкой В. Угол АЕВ прямой, как вписанный, опирающийся на диаметр; угол ВДС также прямой. Следовательно, ВЕ  перпендикулярна АС и ВД перпендикулярна АС. Через точку В проходят два перпендикуляра к прямой АС.

Где ошибка???

Рассуждения, о том, что из точки на прямой можно опустить два перпендикуляра, опирались на ошибочный чертеж. В действительности полуокружности пересекаются со стороной АС в одной точке, т.е. ВЕ совпадает с ВD. Значит, из одной точки на прямой нельзя опустить два перпендикуляра.

 

2. « Спичка вдвое длиннее телеграфного столба»

 

 Пусть  а дм- длина спички и b дм - длина столба. Разность между b и  a  обозначим через c .

Имеем  b - a = c, b = a + c. Перемножаем два эти равенства по частям, находим: b² - ab = ca + c². Вычтем из обеих частей bc. Получим: b²- ab - bc = ca + c² - bc, или b(b - a - c) = - c(b - a - c), откуда

b = - c, но c = b - a, поэтому b = a - b, или a = 2b.    

Где ошибка???

В выражении b(b-a-c )= -c(b-a-c) производится деление на (b-a-c), а этого делать нельзя, так как b-a-c=0.Значит, спичка не может быть вдвое длиннее телеграфного столба.

3. «Катет равен гипотенузе»

 

Угол С равен 90^о, ВД - биссектриса угла СВА, СК = КА, ОК перпендикулярна СА, О - точка пересечения прямых ОК и ВД, ОМ перпендикулярна АВ, ОL перпендикулярна ВС. Имеем: треугольник LВО равен треугольнику МВО, ВL = ВМ, ОМ = ОL = СК = КА, треугольник КОА равен треугольнику ОМА (ОА - общая сторона, КА = ОМ, угол ОКА и угол ОМА - прямые), угол ОАК = углу МОА, ОК = МА = СL, ВА = ВМ + МА, ВС = ВL + LС, но ВМ = ВL, МА = СL, и потому ВА = ВС.

Где ошибка???

 

Рассуждения, о том, что катет равен гипотенузе опирались на ошибочный чертеж. Точка пересечения прямой, определяемой биссектрисой ВD и серединного  перпендикуляра к катету АС, находится вне треугольника АВС.

 

Арифметические софизмы.

1. « Если А больше В, то А всегда больше, чем 2В»

 

Возьмем два произвольных положительных числа А и В, такие, что                                                                  АВ.

Умножив это неравенство на В, получим новое неравенство АВВ*В, а отняв от обеих его частей А*А, получим неравенство АВ-А*АВ*В-А*А, которое равносильно следующему:

                        А(В-А)(В+А)(В-А).      (1)

После деления обеих частей неравенства (1) на В-А получим, что

                        АВ+А (2),

А прибавив к этому неравенству почленно исходное неравенство АВ, имеем 2А2В+А, откуда

                                А2В.

Итак, если АВ, то А2В. Это означает, к примеру, что из неравенства 65 следует, что 610.

Где ошибка???

 

Здесь совершен неравносильный переход от неравенства (1) к неравенству (2).

Действительно, согласно условию АВ, поэтому В-А

2.     «Один рубль не равен ста копейкам»

 

Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е.

        Если a=b, c=d, то ac=bd.

 Применим это положение к двум очевидным равенствам

                                             1 р.=100 коп,  (1)

                                             10р.=10*100коп.(2)

перемножая эти равенства почленно, получим

                                              10 р.=100000 коп.     (3)

и, наконец, разделив последнее равенство на 10 получим, что

                              1 р.=10 000 коп.

таким образом, один рубль не равен ста копейкам.

Где ошибка???

 

Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.

Действительно, перемножая равенства (1) и (2), мы получим не (3), а следующее равенство

                               2                                2

                       10 р.  =100 000 к . ,

которое после деления на 10 дает

                               2                                    2

                        1 р.  = 10 000 коп.,         (*)

а не равенство 1р=10 000 к, как это записано в условии софизма. Извлекая квадратный корень из равенства (*), получаем верное равенство     1р.=100 коп.

3.     «Число, равное другому числу, одновременно и больше, и меньше его».

 Возьмем  два произвольных положительных равных числа А и В и напишем и напишем для них следующие очевидные неравенства:

                          А-В и В-В.       (1)

Перемножив оба этих неравенства почленно, получим неравенство

     А*ВВ*В, а после его деления на В, что вполне законно, ведь В0, придем к выводу, что 

                                   АВ.              (2)

Записав же два других столь же бесспорных неравенства

                       В-А и А-А,                  (3)

Аналогично предыдущему получим, что В*АА*А, а разделив на А0, придем к неравенству

                       АВ.                           (4)

Итак, число А, равное числу В, одновременно и больше, и меньше его.

Где ошибка???

Здесь совершен неравносильный переход от одного неравенства к другому при недопустимом перемножении неравенств.

Проделаем правильные преобразования неравенств.

Запишем неравенство (1) в виде А+В0, В+В0.

Левые части этих неравенств положительны, следовательно, умножая почленно оба эти неравенства

                     (А+В)(В+В)0, или А-В,

что представляет собой просто верное неравенство.

Аналогично предыдущему, записывая неравенства (3) в виде

                      (В+А)0, А+А0, получим просто верное неравенство В-А.

4.     «Ахиллес никогда не догонит черепаху»

Древнегреческий философ Зенон доказывал, что Ахиллес, один из самых сильных и храбрых героев, осаждавших древнюю Трою, никогда не догонит черепаху, которая, как известно, отличается крайне медленной скоростью передвижения..

Вот примерная схема рассуждений Зенона. Предположим, что Ахиллес и черепаха начинают свое движение одновременно, и Ахиллес стремится догнать черепаху. Примем для определенности, что Ахиллес движется в 10 раз быстрее черепахи, и что их отделяют друг от друга 100 шагов.

Когда Ахиллес пробежит расстояние в 100 шагов, отделяющее его от того места, откуда начала двигаться черепаха, то в этом месте он туже ее не застанет, так как  она пройдет вперед расстояние в 10 шагов. Когда Ахиллес минует и эти 10 шагов, то и там черепахи уже не будет, поскольку она успеет перейти на 1 шаг вперед. Достигнув и этого места, Ахиллес опять не найдет там черепахи, потому что она успеет пройти расстояние, равное 1/10 шага, и снова окажется несколько впереди его. Это рассуждение можно продолжать до бесконечности, и придется признать, что быстроногий  Ахиллес никогда не догонит медленно ползающую черепаху.

Где ошибка???

Рассматриваемый софизм Зенона даже на сегодняшний день далек от своего окончательного разрешения, поэтому здесь я обозначу только некоторые его аспекты.

Сначала определим время t, за которое Ахиллес догонит черепаху. Оно легко находится из уравнения a+vt=wt, где а -расстояние между Ахиллесом и черепахой до начала движения, v и w – скорости черепахи и Ахиллеса соответственно. Это время при принятых в софизме условиях  (v=1 шаг/с и w=10 шагов/с) равно 11, 111111… сек.

Другими словами, примерно через 11, 1 с. Ахиллес догонит черепаху. Подойдем теперь к утверждениям софизма с точки зрения математики, проследим логику Зенона. Предположим, что Ахиллес должен пройти столько же отрезков, сколько их пройдет черепаха. Если черепаха  до момента встречи с Ахиллесом пройдет m отрезков, то Ахиллес должен пройти те же m отрезков плюс еще один отрезок, который разделял их до начала движения. Следовательно, мы приходим к равенству m=m+1, что невозможно. Отсюда следует, что Ахиллес никогда не догонит черепаху!!!

Итак, путь, пройденный Ахиллесом, с одной стороны, состоит из бесконечной последовательности отрезков, которые принимают бесконечный ряд значений, а с другой стороны, эта бесконечная последовательность, очевидно не имеющая конца, все же завершилась, и завершилась она своим пределом, равном сумме геометрической прогрессии.

Трудности, которые возникают при оперировании понятиями непрерывного и бесконечного и столь мастерски вскрываются парадоксами и софизмами Зенона, до сих пор не преодолены, а разрешение противоречий, содержащихся в них, послужило более глубокому осмыслению основ математики.

Заключение.

О математических софизмах можно говорить бесконечно много, как и о математике в целом. Изо дня в день рождаются новые парадоксы, некоторые из них останутся в истории, а некоторые просуществуют один день. Софизмы есть смесь философии и математики, которая не только помогает развивать логику и искать ошибку в рассуждениях. Буквально вспомнив, кто же такие были софисты, можно понять, что основной задачей было постижение философии. Но тем не менее, в нашем современном мире, если и находятся люди, которым интересны софизмы, в особенности математические, то они изучают их как явление только со стороны математики, чтобы улучшить навыки правильности и логичности рассуждений.

Понять софизм как таковой (решить его и найти ошибку) получается не сразу. Требуются определенный навык и смекалка. Что касается меня, то некоторые софизмы приходилось разбирать по нескольку раз, чтобы действительно в них разобраться, некоторые же наоборот, казались очень простыми. Развитая логика мышления поможет не только в решении каких-нибудь математических задач, но еще может пригодиться в жизни.

Исторические сведения о софистике и софистах помогли мне разобраться, откуда же все-таки началась история софизмов. По началу, я думала, что софизмы бывают исключительно математические. Причем в виде конкретных задач, но, начав исследование в этой области, я поняла, что софистика-это целая наука, а именно математические софизмы - это лишь часть одного большого течения.

Исследовать софизмы действительно очень интересно и необычно. Порой сам попадаешься на уловки софиста, на столь безукоризненность его рассуждений. Перед тобой открывается какой-то особый мир рассуждений, которые поистине кажутся верными. Благодаря софизмам и парадоксам можно научится искать ошибки в рассуждениях других, научится грамотно строить свои рассуждения и логические объяснения. Если есть желание, то можно стать искусным софистом, добиться исключительного мастерства в искусстве красноречия или просто на досуге проверить свою смекалку. 

Список литературы.

          

1.    А.Г. Мадера, Д.А. Мадера  «Математические софизмы»

Москва, «Просвещение», 2003г.

2.    Ф.Ф. Нагибин, Е.С. Канин «Математическая шкатулка»

Москва, «Просвещение», 1988г.

3.    «Большая энциклопедия Кирилла и Мефодия 2004г.»

4.    www.peterlife.ru/download%20free%20online/humanities/fl_5_a5.htm

5.    www.tmn.fio.ru/works/60x/306/06_2.htm

6.    www.golovolomka.hobby.ru/books/gardner/gotcha/ch2/02.html

7.    www.referats.net

8.    www.ug.ru

9.    www.cultinfo.ru/fulltext/1/001/008/104/779.htm

Математичеcкие софизмы.
(Fallacies)

Математический парадокс можно определить как истину, настолько противоречащую нашему опыту, интуиции и здравому смыслу, что в нее трудно поверить даже после того, как мы шаг за шагом проследим все ее доказательство. Математическим софизмом принято называть не менее удивительные утверждения, в доказательствах которых в отличие от доказательства парадоксов кроются незаметные, а подчас и довольно тонкие ошибки. В любой области математики — от простой арифметики до современной теоретико-множественной топологии — есть свои псевдодоказательства, свои софизмы. В лучших из них рассуждения с тщательно замаскированной ошибкой позволяют приходить к самым невероятным заключениям. Ошибкам в геометрических доказательствах Евклид посвятил целую книгу, но до наших дней она не дошла, и нам остается лишь гадать о том, какую невосполнимую утрату понесла из-за этого элементарная математика.

Семь математических софизмов, о которых пойдет речь в этой главе, выбраны из разных областей математики, каждый из них по-своему интересен. Объяснять, в чем состоит ошибочность рассуждения в каждом софизме, мы не будем, чтобы не лишать читателя удовольствия самостоятельно найти ее.

Наш первый софизм чрезвычайно элементарен. Мы предпошлем ему занимательный парадокс, на примере которого великий немецкий математик Давид Гильберт любил объяснять необычные свойства наименьшего из трансфинитных чисел «алеф-нуль». Как-то раз хозяину одной великолепной гостиницы с бесконечным, но счетным числом номеров, ни один из которых не был свободен, нужно было принять нового гостя. Хозяин вышел из положения очень просто: каждого из своих постояльцев он переселил в комнату, номер которой был на единицу больше номера прежней комнаты, в результате чего обитатель n-й комнаты переехал в (n + 1)-ю и освободил для нового гостя самую первую комнату. Как может поступить хозяин, если прибудет бесконечное множество новых гостей? Ничуть не смущаясь, хозяин переселяет всех своих прежних постояльцев в комнаты с вдвое большими номерами (гость из комнаты 1 переезжает в комнату 2, гость из комнаты 2 — в комнату 4, гость из комнаты 3 — в комнату 6, гость из комнаты 4 — в комнату 8 и т. д.) и размещает вновь прибывших в освободившихся комнатах с нечетными номерами.

Но так ли необходимо хозяину иметь счетное число комнат для того, чтобы разместить новых гостей? В приведенных ниже стишах, взятых из одного английского журнала, выходившего в прошлом веке, рассказывается о хитром хозяине гостиницы, сумевшем разместить в девяти номерах десять гостей так, что каждому из них досталось по отдельной комнате.

Их было десять чудаков, Тех спутников усталых, Что в дверь решили постучать Таверны «Славный малый». — Пусти, хозяин, ночевать, Не будешь ты в убытке, Нам только ночку переспать, Промокли мы до нитки. Хозяин тем гостям был рад, Да вот беда некстати: Лишь девять комнат у него И девять лишь кроватей. — Восьми гостям я предложу Постели честь по чести, А двум придется ночь проспать В одной кровати вместе. Лишь он сказал, и сразу крик, От гнева красны лица: Никто из всех десятерых Не хочет потесниться. Как охладить страстей тех пыл, Умерить те волненья? Но старый плут хозяин был И разрешил сомненья.

Двух первых путников пока, Чтоб не судили строго, Просил пройти он в номер «А» И подождать немного. Спал третий в «Б», четвертый в «В», В «Г» спал всю ночь наш пятый, В «Д», «Е», «Ж», «3» нашли ночлег С шестого по девятый. Потом, вернувшись снова в «А», Где ждали его двое, Он ключ от «И» вручить был рад Десятому герою. Хоть много лет с тех пор прошло, Неясно никому, Как смог хозяин разместить Гостей по одному. Иль арифметика стара, Иль чудо перед нами, Понять, что, как и почему, Вы постарайтесь сами.

Примером более тонкого математического софизма служит следующее «алгебраическое» доказательство того, что любое число а равно меньшему числу b.

Начнем с равенства

а = b + c.

Умножив обе его части на a — b, получим

а² — аb = аb + аc — b² — be.

Перенесем ас в левую часть:

а² — аb — аc = аb — b² — be

и разложим на множители:

а(а — b — c) = b(а — b — c).

Разделив обе части равенства на а — b — c, найдем

а = b,

что и требовалось доказать.

Много неприятностей подстерегает того, кто неосторожно обращается с мнимой единицей i (квадратным корнем из -1). Об этом свидетельствует хотя бы следующее удивительное «доказательство» равенства 1 = -1:

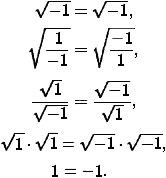
Рис. 82. Треугольник Керри.

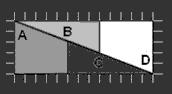
В планиметрии большая часть ошибочных доказательств связана с использованием неправильных чертежей. Рассмотрим, например, удивительное «доказательство» того, что площадь лицевой стороны многоугольника, вырезанного из бумаги, отличается от площади оборотной стороны того же многоугольника. Это «доказательство» придумано врачом-психиатром Л. Восбургом Лионсом, в нем используется один любопытный принцип, открытый П. Керри.

Прежде всего начертим на листке бумаги в клетку треугольник, площадь которого равна 60 клеткам (рис. 82), и разрежем его вдоль прямых, показанных на верхнем рисунке. Перевернув части треугольника на другую сторону и составив из них треугольник, изображенный на рис. 82 в середине, мы обнаружим, что в центре нового треугольника появилась дырка площадью в 2 клетки. Иначе говоря, суммарная площадь частей исходного треугольника при переворачивании уменьшилась до 58 клеток! Перевернув еще раз (лицевой стороной вверх) лишь три части исходного треугольника, мы сможем составить из всех шести частей фигуру, изображенную на рис. 82 внизу. Ее площадь равна 59 клеткам. Что-то здесь не так, это ясно, но что именно?

Теория вероятностей изобилует правдоподобными, но логически не безупречными рассуждениями. Предположим, что вы встретились со своим другом Джоном и что каждый из вас носит тот галстук, который ваша жена подарила ему на Рождество. Вы начинаете спорить о том, чей галстук дороже, и в конце концов решаете пойти в магазин, где были куплены галстуки, и узнать, сколько стоит каждый из них. Тот, кто выиграет (чей галстук окажется дороже), по условию пари должен отдать свой галстук проигравшему, чтобы смягчить горечь поражения.

Вы рассуждаете так: «Шансы выиграть и проиграть у меня одинаковые. Выиграв, я обеднею на сумму, равную стоимости моего галстука. Проиграв, я получу более дорогой галстук. Следовательно, заключив пари, я окажусь в более выгодном положении, чем мой приятель».

Разумеется, ничто не мешает Джону рассуждать точно так же. Могут ли обе стороны, заключившие пари, иметь преимущество друг перед другом?

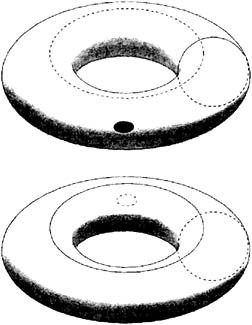
Один из наиболее впечатляющих парадоксов топологии заключается в том, что тор (поверхность бублика), если его поверхность растягивать (не разрывая при этом), можно вывернуть наизнанку через любую сколь угодно малую дырочку. Никакой проблемы здесь нет. Но уж если тор действительно можно вывернуть наизнанку, то следует обратить внимание и еще на один, пожалуй, даже более замечательный факт.

Рис. 83. Если тор вывернуть наизнанку, то кажется, что кольца, нарисованные на его поверхности, расцепляются.

        На наружной стороне тора проведем меридиан (рис. 83, вверху). На внутренней стороне того же тора проведем параллель. Обе эти окружности, очевидно, сцеплены между собой. Вывернем теперь тор наизнанку через дырочку в его поверхности. Как видно из нижнего рисунка, первая окружность перейдет с наружной поверхности тора внутрь, а вторая — наружу, и обе окружности окажутся расцепленными! Очевидно, что это нарушает фундаментальный топологический закон, который гласит: разделить две сцепленные замкнутые кривые можно, лишь разорвав одну из кривых и протащив через место разрыва вторую.
        В нашем последнем софизме, заимствованном из элементарной теории чисел, речь пойдет о сравнительных достоинствах «интересных» чисел. Разумеется, числа могут представлять интерес с различных точек зрения. Так, для Джорджа Мура, когда он писал свою знаменитую оду тридцатилетней женщине, особый интерес представляло число 30 — Мур считал, что в этом возрасте замужние женщины особенно привлекательны. Для специалиста по теории чисел число 30 представляет, по-видимому, еще больший интерес, поскольку это наибольшее из чисел, обладающих тем свойством, что все меньшие числа, не имеющие с ними общих делителей, про­сты. Число 15 873 также небезынтересно: если его умножить сна­чала на любую цифру, то есть на любое из чисел от 1 до 9, а затем на 7, то результат будет состоять из повторений выбранной для первого умножения цифры. Еще более удивительными свойствами обладает число 142 857: умножая его на числа от 1 до 6, вы будете получать циклические перестановки одних и тех же шести цифр.
        Возникает вопрос: существуют ли неинтересные числа? С помощью элементарных рассуждений нетрудно доказать, что неинтересных чисел нет. Если бы скучные числа существовали, то все числа можно было бы разбить на два класса: интересные числа и неинте­ресные, скучные числа. Во множестве неинтересных чисел нашлось бы одно число, которое было бы наименьшим из всех неинтересных чисел. Но наименьшее из всех неинтересных чисел — это уже число само по себе интересное. Поэтому мы должны были бы изъять его из множества неинтересных чисел и перевести в другое множество. В оставшемся множестве в свою очередь нашлось бы наименьшее число. Повторяя этот процесс достаточно долго, можно сделать ин­тересным любое неинтересное число.

* * *

Наибольшее беспокойство читателям доставил софизм с вывернутым наизнанку тором. Тор действительно можно вывернуть наизнанку, но это изменяет его ориентацию. В результате обе окружности меняются местами и остаются в зацеплении. Если отрезать нижнюю часть чулка и сшить концы в трубку, получится превос­ходная модель тора. На ней нитками различных цветов можно про­стегать меридиан и параллель. Такой тор легко вывернуть через дырочку в поверхности, при этом прекрасно видно все, что проис­ходит с меридианом и параллелью.

Подробное объяснение софизма с треугольником и некоторые другие головоломки можно найти в двух главах «Исчезновение фигур» моей книги «Математические чудеса и тайны»**. Софизм с галстуком подробно разобран у М. Крайчика***.

Заключительное «доказательство» того, что неинтересных чисел не существует, вызвало следующую телеграмму читателя:

Немедленно прекратите вылавливать неинтересные числа и превращать их в интересные. Для интереса оставьте хоть одно неинтересное число!

 Процесс познания человеком окружающего мира можно сравнить с радостным торжеством, ибо каждая раскрытая тайна укрепляет веру в свои силы. Но на пути победоносной человеческой мысли возникают большие, казалось бы непреодолимые, преграды, перед которыми были бессильными умозаключения. Древнегреческий философ Диодор Кронос (примерно307 год до н.э) не решив одну из древнейших логических задач - парадокс Эвклида, умер от разочарования, а другой философ Фигет Косский, познав такую же неудачу, покончил жизнь самоубийством. Древнегреческие ученые сталкивались с такими задачами в математике. Они прикладывали много усилий, чтобы выявить механизм образования таких загадок. Было установлено, что наши рассуждения тоже подчинены определенным законам (законам логики), нарушение которых обесценивает результаты, добытые в этих рассуждениях. Неразрешенность задач, с которыми встретились Диодор Кронос и Фигет Косский, объясняется как правило, нарушением законов логики. Поэтому уже тогда остро встал вопрос о системе "профилактических приемов" -определенных правил с целью устранения логических ошибок. Первая в истории проба проведения "логической профилактики" в математике принадлежит гениальному древнегреческому математику, автору "Начал" - Эвклиду (IV в до н.э.)Он создал удивительный сборник "Псевдарий", где помещая разнообразные ошибочные рассуждения, к которым часто приходят те, кто начинает играть в математику. Таким образом, Эвклид был автором первого из известных сборников математических софизмов и парадоксов. Остается сожалеть, что этот труд не дошел до нас. Зато требовательность Эвклида и строгость к культуре рассуждений нашла многочисленных последователей. Они собрали и опубликовали большую коллекцию математических софизмов и парадоксов. В наше время ученые продолжают это дело совсем не для того, чтобы удивить кого-то. Человеку свойственно ошибаться, поэтому очень важно, чтобы он умел выявлять свои и чужие ошибки, учился избегать их. Действительно, чем хитрее софизм, чем искустнейше замаскирована ошибка, тем больше удовлетворения приносит он тому кто разгадал его, так как это - маленькое открытие и прекрасная школа, культура математических вычислений. Сборники математических софизмов и парадоксов были всегда популярными. Так в 1846 году М.Г.Чернышевский писал брату Александру:"... сижу 11 недель и 3 дня и никак не разгрызу орешек. Нe поможешь ли мне? Я дал слово не вставать со стула, пока не решу эту задачу. Но что-то не удаётся; помоги хоть ты, лишь на тебя надежда. Вот она. Квадрат любой стороны в любом треугольнике равен сумме квадратов двух других сторон." М.Г.Чернышевский поместил в письме рисунок и доказательства, которые привели к интересному софизму (этот софизм приведен далее).

      Этот доклад не просто предлагает задачи из занимательной математики, но и приглашает в своеобразное путешествие неспокойными дорожками человеческой мысли.

"Людям, которые желают идти верной дорогой, важно также знать и об отклонениях." Аристотель

      Что такое истина?

      В философском понятии истина есть вполне определенное отображение человеком реальной действительности предмета познания таким, каким он есть независимо от нашего сознания и вне его. Истина занимает особое место в жизни человека. Она приносит радость и огорчение, увлекает и вызывает злость, парализует волю слабых и ведет на подвиги сильных. Выдающийся древнегреческий философ материалист Демокрит (460-370 лет до н.э.) говорил, что доказательство теоремы ему дороже чем царственный престол. Великий итальянский ученый Джордано Бруно (1548 - 1600) познал жестокие преследования и пошел на огонь инквизиции ради научной истины. В 1820 году венгерский математик Фархаш Бойян писал своему сыну Яношу, когда узнал, что тот берется за доказательство V постулата Эвклида: "Ты не должен пытаться одолеть теорию параллельных линий: я знаю этот путь, я прошел его до конца, я пережил эту беспросветную ночь и весь свет, всю радость моей жизни я похоронил в нем. Молю тебя забудь учение параллельных оно лишит тебя здоровья, потом оно лишит тебя радости жизни. Это - беспросветная тьма может поглотить тысячами таких талантов, как Ньютон... Я готов был стать мучеником этой истины, чтобы только очистить геометрию от этого пятна. Я проделал страшную, гигантскую работу, я достиг значительно больше, чем то, что было найдено до меня, но полного удовлетворения я не получил!" Предупреждения были напрасными. Янош Бойян прошел весь трудный путь по раскрытию тайны параллельных прямых, познал радостные минуты первооткрывателя и горькие часы и даже годы непризнания его парадоксальных в то время результатов.

      Пытливая человеческая мысль проявляла неисчерпаемую находчивость, изворотливость и силу, отвоевывая её тайны. То, что казалось очевидным, часто оказывалось ошибкой. Люди наблюдают, как "Солнце вращается вокруг Земли", в действительности это движение есть зрительное следствие движения Земли вокруг Солнца и своей оси. А сколько неправильной информации поступает от наших органов чувств, когда оцениваются расстояния, размеры тел, отрезки времени, положение предметов в пространстве, их цвет. В " Сфинксе " Эдгар По описывает такой случай с героем рассказа; " Дело в том", что скоро по приезду в коттедж со мной случилось что-то непонятное и зловещее... Я был настолько потрясен, что прошло много дней, прежде чем я отважился рассказать об этом моему товарищу. В конце жаркого дня я сидел с книжкой в руках около открытого окна, откуда открывался вид на берег речки и на отдаленный пригорок, с ближайшего к нам бока - безлесный, вследствие, так называемого оползня. Мысли так давно уже оторвались от книжки и, отведя глаза от страницы, я увидел оголенный склон, а на нем мерзкую тварь, которая быстро спускалась с пригорка и скрылась в густом лесу около его подножья. При появлении этого существа я сначала подумал, что я сошел с ума, но во всяком случае не поверил своим глазам. Прошло немало времени, прежде чем я убедился, что не сплю и не сошел с ума. Но если я опишу тварь, которую я четко увидел и имел возможность наблюдать, пока она спускалась по склону, читателям ещё труднее чем мне будет в неё поверить. "Страшной тварью оказалась... кошка , которая проползла по паутине вдоль оконной рамы. Сопоставления и гиперболизация воображаемых образов заставили героя рассказа пережить минуты глубокого потрясения.

      Чтобы избежать подобных ситуаций человек с первых шагов своей деятельности прибегает к другому методу познания мира, который помогал не только критиковать, но и корректировать познания через органы чувств. Этим методом стало мышление. Только благодаря мышлению удаётся объяснить и уточнить факты, выявленные в результате наблюдений и опытов. Высшей формой умственной деятельности человека есть теоретическое мышление. Среди различных теоретических методов познания мира наиболее мощным стал математический метод. Он занял особое место в познании по масштабам применения. Выдающийся 41ранцузский философ и математик Пьер Гассенди (1592 - 1635) писал: "Тот, кто с детства проникся математикой, усвоив её непростые доказательства, так подготовлен к принятию истины, что легко отбросит любую фальшь."

      Математика важна для студента не только как основа дальнейшего технического и профессионального обучения. Она важна потому, что учит его точному и правильному мышлению. А мыслить правильно нужно всем: инженеру, ученому, врачу, писателю, артисту.

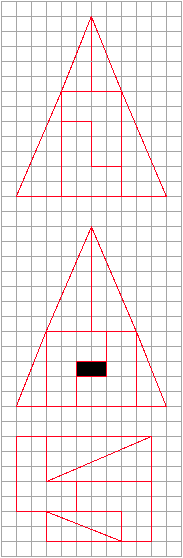
Софизм 65=64.

Рисунок 1

Рисунок 2

      На рисунке 1 имеем на клетчатой бумаге нарисованный прямоугольник размерами 5 x 13, т.е. площадью 65. На рисунке 2 имеем квадрат 8 x 8 = 64. Обе фигуры разрезаны на попарно равные части. Отсюда, их площади равны; следовательно, 64 = 65.

      В этом софизме проявляется еще одно интересное свойство чисел Фибоначчи (он же Леонардо Пизанский (1180 - 1240), итальянский математик). Вкратце это так: первоначальный прямоугольник 5 x 13 разрезан на такие части, что 5 + 8 = 13 (по оси x). Квадрат же составлен 8 x 8, т.е. среднее между числами 5 и 13 в ряде Фибоначчи.

      Софизм равенства катета гипотенузе, или все треугольники равносторонние.

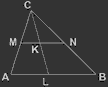
      Рассмотрим произвольный треугольник ABC(рис.3). Проведем биссектрису угла B и серединный перпендикуляр к стороне AC; точку их пересечения назовем O. Опустим из нее перпендикуляры EO и OF на стороны AB и BC соответственно.

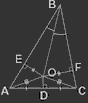
Рисунок 3

      Т.к. DO одновременно и высота и медиана треугольника AOC, то он равнобедренный и AO = OC. Т.к. BO - биссектриса, то, из равенства треугольников EBO и OBF (откуда EB = BF), EO = OF. Следовательно, треугольник AEO равен треугольнику FCO, т.е. AE = FC. Отсюда, т.к. AB = AE + EB и BC = BF + FC, AB = BC. Проведя такое же рассуждение для основания не AC, а, например, AB, получим, что BC = CA.

      Из этого следует, что все треугольники на свете - равносторонние. В частном случае, если треугольник прямоугольный, то катеты равны гипотенузе.

      Софизм, названный мною "парадоксом" равных отрезков, или полуокружность длиннее прямой.

Рисунок 4

Рисунок 5

      Рассмотрим треугольник ABC(рис.5). Проведем прямую MN параллельно AB так, как показано на рисунке. Теперь для любой точки L стороны AB проведем прямую CL, которая пересечет MN в точке K. Таким образом установим однозначное соответствие между отрезками AB и MN, т.е. они оба содержат одинаковое количество точек. Значит, имеют одинаковую длину.

      Аналогичным способом для любой точки K(рис.4) полуокружности MN установим однозначное соответствие с точками прямой a. Но у нас останутся две точки, а именно M и N, для которых это соответствие не установим. Следовательно, в полуокружности на две точки больше, а значит, полуокружность длиннее прямой.

*В класс Арифмантики вошла неспешно четверокурсница. Она прошла мимо рядов парт, поглядывая на лица студентов, подошла к преподавательскому столу и обернулась, сияя радостной улыбкой именинницы*

Доброго дня, товарищи студенты! Добро пожаловать на лекцию Магии Чисел, и рада сообщить, что в период Самоуправления я буду вести у вас этот предмет. Прошу называть меня weila, и - в такой знаменательный период - всё-таки добавляйте слово «профессор»;)
Наша сегодняшняя лекция, как вы могли понять по надписи на доске, посвящена математическим парадоксам. Перейдём прямо к материалу урока, чтобы вы не скучали…

*профессор постучала волшебной палочкой по столу, и две студентки, рассматривавшие под партой новый выпуск «Оракула», смущённо посмотрели на преподавателя*

…Итак, издревле математики стали замечать, что порой их суждения не столь обоснованы, как хотелось бы, а иногда и вовсе противоречат логике. Их сей факт, естественно, задел, и они дали красивое название таким математическим несовпадениям – парадоксы (от греческого слова «paradoxos», которое значит – «противоречащий обычному мнению»). Часто действительно в парадоксах одна аксиома натыкалась на другую, и они между собой «конкурировали» - победа не могла достаться ни той, ни другой также по практически аксиоме. Вот, к примеру, известные в математическом кругу парадоксы.

*учитель взмахнула палочкой, из её стола вырвался свиток больших размеров и развернулся перед учениками*

Парадокс Рассела. А иначе – парадокс брадобрея.

В одном городе брадобрей бреет всех жителей, которые не бреют себя сами. Вопрос: кто бреет тогда самого брадобрея? Ведь если он бреется сам, это противоречит условию – тогда он бреет не только тех жителей, которые не бреются сами, но и одного жителя, который бреется сам. Если он бреется не сам, то он не бреет всех жителей городка, которые не бреются сами.

Вчитались?) Смотрите, как противоречивы ответы – ни один нельзя признать верным. Теперь
взгляните-ка на ещё один свиток, совсем короткий:

Парадокс "Куча".
Одна песчинка не есть куча песка. Если n песчинок не есть куча песка, то и n + 1 песчинка - тоже не куча. Следовательно, никакое число песчинок не образует кучу песка.

И здесь мы с вами обнаружили противоречие, не так ли?
Вот и математики в своё время поделились на две группы: интуиционистов и их противников. Первые заявили, что с появлением парадоксов стало ясно – наука математика изначально неверна в своих положениях. Но, к счастью всего современного человечества, вторых было больше, и они смогли опровергнуть все заявления интуиционистов. Ведь всем известно – не бывает правил без исключений.
Например, парадокс "Куча" формалисты - противники интуиционистов - объяснили тем, что куча
песка - это неопределённое понятие, и здесь нельзя применять математические методы (в парадоксе как раз использован метод индукции).

Итак, вы могли на примере ощутить, что же такое математический парадокс. Но иногда мы можем спутать истинно логичное рассуждение с некими другими понятиями - например, в магии чисел или же в других науках. Примером могут послужить софизмы. Кто знает, что это такое?

*поднялась рука ученика на третьей парте, и он стал отвечать: "Ну, софизмы это что-то вроде математических фокусов… Это очевидно верные рассуждения, но в них часто какой-то подвох. Софизмы… они… они… опровергают аксиомы, но при тщательном рассмотрении теряют всякую истинную подоплёку…"*

В общем, верно, - профессор улыбнулась, - Но запишите определение, чтобы не забыть:

Софизм - формально кажущееся правильным, но ложное по существу умозаключение, основанное на преднамеренном нарушении правил логики.

А ты мог бы нам привести пример софизма? – обратилась преподаватель к ученику.

*Тот смущённо встал, вышел к доске и начал рассказывать:

"Мне рассказывала бабушка. Вот, как-то раз к продавщице мороженого пришёл необычайно хитрый покупатель. Он протянул ей десять монет по 5 копеек и заказал мороженое. Продавщица удивилась:

- Мороженое-то стоит 5 рублей! А у вас 50 копеек.
- Смотрите, полрубля равно пяти копейкам, а полрубля по десять раз, - он потряс монетками в руке, - это и есть 5 рублей.
- Но ведь пять копеек - не пол-рубля!
- А как же? Смотрите. 1/4 рубля = 25 копеек. Извлечём корень из обеих частей равенства. Получится: 1/2 рубля=5 копеек.
- А в рубле-то 100 копеек!
- Да смотрите же: 100 копеек = 1 рубль. Опять извлечём корень из обеих частей. 10 копеек = 1 рубль.
Вот так покупатель обхитрил продавщицу".

Студент обернулся к профессору, увидел, что та кивнула, и отправился на своё место*

Вот видите, как легко порой запутать человека! Но ваша задача, как образованных магов, не попадаться под уловки таких хитрецов, которые пользуются софизмами в неблагородных целях.
Привести ещё пример? Что ж. Я могу написать вам ещё одно доказательство такого "факта" – дважды два равно пяти. Посмотрите теперь на карточки прямо перед вами на партах.



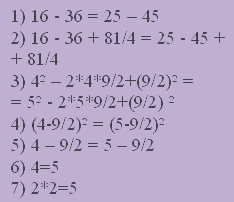
Здесь достаточно помнить формулу о квадрате разности, чтобы всё понять) Но, спрашивается, если всё верно, то как же быть со всем известной аксиомой? Или опять парадокс? Нет, всего лишь софизм, а в чём тут «фокус», я вам сейчас объясню. Взгляните на новые карточки перед вами, и вы увидите, в чем загадка этого софизма.



На самом деле верным доказательство этого софизма назвать нельзя, и поэтому его авторы нарочно забыли про то, что уместным было бы поставить знак "плюс-минус", вынося выражение из-под знака квадрата. Такое доказательство противоречит основным научным законам, потому и не воспринимается всерьёз.

Порой к парадоксам сводят совсем нелепые доказательства. Но в каждой шутке, в том числе и нелепости, есть доля правды. Например, находят неточности в формулировках теорем. Снова взгляните на карточки:



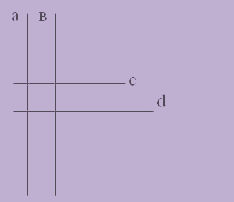
а по условию параллельно в. с в свою очередь параллельно d. а и в – параллельные прямые, они пересекаются с с и d – параллельными прямыми. Вывод: параллельные прямые пересекаются. Но такие явные попытки ввести в заблуждение не должны вас запутать – вы теперь сможете отличить истинный парадокс от софизма или вовсе наивных попыток вроде вышеописанной)

Что ж – наша лекция окончена, а теперь обратите внимание на домашнее задание, которое поможет усвоить материал.

1) Приведите пример парадокса и объясните, в чём именно заключено противоречие, по вашему мнению. А, быть может, вы приведёте в качестве примера вовсе не истинный парадокс, а софизм – тогда уж постарайтесь объяснить, что в нём является неверным.

2) Всё же разгадайте загадку софизма с мороженщицей, описанного в лекции. В чём заключается хитрость, которая ввела её в заблуждение?

3) Ответьте на вопрос задачки под названием "Дилемма крокодила": "Крокодил украл ребенка и пообещал отцу вернуть его, если отец угадает - вернет ему крокодил малыша или нет. Что должен сделать крокодил, если отец скажет, что крокодил не вернет ему ребенка?"

К сведению:
- Помните, что важную роль играет общее впечатление от домашней работы.
- Она должна по объёму составлять не менее одного листа Word, 12-м размером шрифта Times New Roman.
- Использование фантазии настоятельно рекомендуется!)
- В качестве доклада Вы можете привести примеры интересных, на ваш взгляд, софизмов или математических парадоксов, которые не были указаны в лекции или Вашей домашней работе. А также я принимаю любые сочинения с дополнительной информацией по теме урока.

Думаю, многие хотя бы раз в жизни слышали подобные высказывания: «Все числа равны» или «два равно трём». Таких примеров может быть очень много, но что же это значит? Кто это придумал? Можно-ли как-то объяснить эти высказывания или всё это – вымысел? На эти вопросы, и на многие другие я хочу ответить в своей работе. Существуют различные софизмы: логические, терминологические, психологические, математические и т.д.

ПОНЯТИЕ «СОФИЗМ»

Софизм – (от греческого sophisma , «мастерство, умение, хитрая выдумка, уловка») - умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям. Софизм, в отличие от паралогизма, основан на преднамеренном, сознательном нарушении правил логики. Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибок. Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. История математики полна неожиданных и интересных софизмов, разрешение которых порой служило толчком к новым открытиям. Математические со-физмы приучают внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записи черте-жей, за законностью математических операций. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать.

ЭКСКУРС В ИСТОРИЮ

Софистами называли группу древнегреческих философов 4-5 века до н.э., достигших большого искусства в логике. В период падения нравов древнегреческого общества( 5 век) появляются так называемые учителя красноречия, которые целью своей деятельности считали и называли приобретение и распространения мудрости, вследствие чего они именовали себя софистами. Наиболее известна деятельность старших софистов, к которым относят Протагора из Абдеры, Горгия из Леонтип, Гиппия из Элиды и Продика из Кеоса. Но суть деятельности софистов много больше, чем простое обучение искусству красноречия. Они обучали и просвещали древнегреческий народ, старались способствовать достижению нравственности, присутствия духа, способности ума ориентироваться во всяком деле. Но софисты не были учеными. Умение, которое должно было быть достигнуто с их помощью, заключалось в том, что человек учился иметь в виду многообразные точки зрения. Аристотель называл софизмом «мнимые доказательства», в которых обос-нованность заключения кажущаяся и обязана чисто субъективному впечатлению, вызванному недостаточностью логического анализа. Убедительность на первый взгляд многих софизмов, их «логичность» обычно связана с хорошо замаскированной ошибкой — семиотической: за счёт метафоричности речи, нарушающих однозначность мысли и приводящих к смешению значений терминов, или же логической: подмена основной мысли (тезиса) доказательства, принятие ложных посылок за истинные, несоблюдение допустимых способов рассуждения (правил логического вывода), использование «неразрешённых» или даже «запрещённых» правил или действий, например деления на нуль в математических софизмах. Исторически с понятием «софизм» неизменно связывают идею о намеренной фальсификации, руководствуясь признанием Протагора, что задача софиста (софист, от греч. sophistes — умелец, изобретатель, мудрец, лжемудрец) — представить наихудший аргумент как наилучший путём хитроумных уловок в речи, в рассуждении, заботясь не об истине, а об успехе в споре или о практической выгоде. С этой же идеей обычно связывают и «критерий основания», сформулированный Протагором: мнение человека есть мера истины. Так, софизм «куча» («Одно зерно — не куча. Если n зё-рен не куча, то n + 1 зерно — тоже не куча. Следовательно, любое число зёрен — не куча») — это лишь один из «парадоксов транзитивности», возникающих в ситуации «неразличимости».

АРИФМЕТИЧЕСКИЕ СОФИЗМЫ

Арифметика - (греч. arithmetika, от arithmys — число), наука о числах, в первую очередь о натуральных (целых положительных) числах и (рацио-нальных) дробях, и действиях над ними. Так что же такое арифметические софизмы? Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.

1. « Если А больше В, то А всегда больше, чем 2В»

Возьмем два произвольных положительных числа А и В, такие, что АВ. Умножив это неравенство на В, получим новое неравенство АВВ*В, а отняв от обеих его частей А*А, получим неравенство АВ-А*АВ*В-А*А, которое равносильно следующему:
А(В-А)(В+А)(В-А). (1)
После деления обеих частей неравенства (1) на В-А получим, что
АВ+А (2),
А прибавив к этому неравенству почленно исходное неравенство АВ, имеем 2А2В+А, откуда
А2В.
Итак, если АВ, то А2В. Это означает, к примеру, что из неравенства 65 следует, что 610.
Где же ошибка???
Здесь совершен неравносильный переход от неравенства (1) к неравенству (2). Действительно, согласно условию АВ, поэтому В-А
2. «Число, равное другому числу, одновременно и больше, и меньше его».

Возьмем два произвольных положительных равных числа А и В и напи-шем и напишем для них следующие очевидные неравенства:
А-В и В-В. (1)
Перемножив оба этих неравенства почленно, получим неравенство А*ВВ*В, а после его деления на В, что вполне законно, ведь В0, придем к выводу, что
АВ. (2)
Записав же два других столь же бесспорных неравенства
В-А и А-А, (3)
Аналогично предыдущему получим, что В*АА*А, а разделив на А0, придем к неравенству
АВ. (4)
Итак, число А, равное числу В, одновременно и больше, и меньше его.
Где ошибка???
Здесь совершен неравносильный переход от одного неравенства к другому при недопустимом перемножении неравенств. Проделаем правильные преобразования неравенств. Запишем неравенство (1) в виде А+В0, В+В0. Левые части этих неравенств положительны, следовательно, умножая почленно оба эти неравенства (А+В)(В+В)0, или А-В, что представляет собой просто верное неравенство. Аналогично предыдущему, записывая неравенства (3) в виде (В+А)0, А+А0, получим просто верное неравенство В-А.

АЛГЕБРАИЧЕСКИЕ СОФИЗМЫ

Алгебра — один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией к числу старейших ветвей этой науки. Задачи, а также методы А., отличающие её от других отраслей математики, создавались постепенно, начиная с древности. Алгебра возникла под влиянием нужд общественной практики, в результате поисков общих приёмов для решения однотипных арифметических задач. Приёмы эти заключаются обычно в составлении и решении уравнений. Т.е. алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях.
1. «Два неодинаковых натуральных числа равны между собой»
решим систему двух уравнений:

х+2у=6, (1)
у=4- х/2 (2)

Сделаем это подстановкой у из 2го уравнения в 1, получаем х+8-х=6, отку-да 8=6
Где же ошибка???
Уравнение (2) можно записать как х+2у=8, так что исходная система за-пишется в виде:

Х+2у=6,
Х+2у=8

В этой системе уравнений коэффициенты при переменных одинаковы, а правые части не равны между собой, из этого следует, что система несо-вместна, т.е. не имеет ни одного решения. Графически это означает, что прямые у=3-х/2 и у=4-х/2 параллельны и не совпадают. Перед тем, Как решать систему линейных уравнений, полезно проанализировать, имеет ли система единственное решение, бесконечно много решений или не имеет решений вообще.

2. «Отрицательное число больше положительного».
Возьмем два положительных числа а и с. Сравним два отношения:
а/-c и -а/c
Они равны, так как каждое из них равно –(а/с). Можно составить пропорцию: a/-c=-a/c
Но если в пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего. В нашем случае а-с, следо-вательно, должно быть –ас, т.е. отрицательное число больше положительного.
Где ошибка???
Данное свойство пропорции может оказаться неверным, если не-которые члены пропорции отрицательны.

3. «Дважды два равно пяти».

Обозначим 4=а, 5=b, (a+b)/2=d. Имеем: a+b=2d, a=2d-b, 2d-a=b. перемножим два последних равенства по частям. Получим: 2da-a*a=2db-b*b. Умножим обе части получившегося равенства на –1 и прибавим к результатам d*d. Будем иметь: a 2-2da+d2=b2 -2bd+d2, или (a-d)(a-d)=(b-d)(b-d), откуда a-d=b-d и a=b, т.е. 2*2=5
Где ошибка???
Из равенства квадратов двух чисел не следует, что сами эти числа равны.

ГЕОМЕТРИЧЕСКИЕ СОФИЗМЫ

Геометрические софизмы – это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.
1. « Спичка вдвое длиннее телеграфного столба»

Пусть, а дм- длина спички и b дм - длина столба. Разность между b и a обозначим через c . Имеем b - a = c, b = a + c. Перемножаем два эти равенства по частям, нахо-дим: b2 - ab = ca + c2. Вычтем из обеих частей bc. Получим: b2- ab - bc = ca + c2 - bc, или b(b - a - c) = - c(b - a - c), откуда b = - c, но c = b - a, поэтому b = a - b, или a = 2b.
Где ошибка???
В выражении b(b-a-c )= -c(b-a-c) производится деление на (b-a-c), а этого делать нельзя, так как b-a-c=0.Значит, спичка не может быть вдвое длиннее телеграфного столба.

ПРОЧИЕ СОФИЗМЫ

Кроме математических софизмов, существует множество других, например: логические, терминологические, психологические и т.д. Понять абсурдность таких утверждений проще, но от этого они не становятся менее интересными. Очень многие софизмы выглядят как лишенная смысла и цели игра с языком; игра, опирающаяся на многозначность языковых выражений, их неполноту, недосказанность, зависимость их значений от контекста и т.д. Эти софизмы кажутся особенно наивными и несерьезными.

«Полупустое и полуполное»
«Полупустое есть то же, что и полуполное. Если равны половины, значит, равны и целые. Следовательно, пустое есть то же, что и полное».

«Чётное и нечётное»
«5 есть 2 + 3 («два и три»). Два — число чётное, три — нечётное, выходит, что пять — число и чётное и нечётное. Пять не делится на два, также, как и 2 + 3, значит, оба числа не чётные!»

«Не знаешь то, что знаешь»
«Знаешь ли ты, о чём я хочу тебя спросить?» — «Нет». — «Знаешь ли ты, что добродетель есть добро?» — «Знаю». — «Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что знаешь».

«Лекарства»
«Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно больше».

«Вор»
«Вор не желает приобрести ничего дурного. Приобретение хорошего есть дело хорошее. Следовательно, вор желает хорошего».

«Отец — собака»
«Эта собака имеет детей, значит, она — отец. Но это твоя собака. Значит, она твой отец. Ты её бьёшь, значит, ты бьёшь своего отца и ты — брат щенят».

«Рогатый»
«Что ты не терял, то имеешь. Рога ты не терял. Значит, у тебя рога».

«Чем больше»
«Чем больше я пью водки, тем больше у меня трясутся руки. Чем больше у меня трясутся руки, тем больше спиртного я проливаю. Чем больше я проливаю, тем меньше я выпиваю. Значит, чтобы пить меньше, надо пить больше».

«Самое быстрое существо не способно догнать самое медленное»
Быстроногий Ахиллес никогда не настигнет медлительную черепаху. Пока Ахиллес добежит до черепахи, она продвинется немного вперед. Он быстро преодолеет и это расстояние, но черепаха уйдет еще чуточку вперед. И так до бесконечности. Всякий раз, когда Ахиллес будет достигать места, где была перед этим черепаха, она будет оказываться хотя бы немного, но впереди.

«Нет конца»
Движущийся предмет должен дойти до половины своего пути прежде, чем он достигнет его конца. Затем он должен пройти половину оставшейся половины, затем половину этой четвертой части и т.д. до бесконечности. Предмет будет постоянно приближаться к конечной точке, но так никогда ее не достигнет.

«Медимн зерна»
Большая масса мелких, просяных например, зерен при падении на землю всегда производит шум. Он складывается из шума отдельных зерен, и, значит, каждое зерно и каждая малейшая часть зерна должны, падая, произво-дить шум. Однако отдельное зерно падает на землю совершенно бесшумно. Значит, и падающий на землю медимн зерна не должен был бы производить шум, ведь он состоит из множества зерен, каждое из которых падает бесшумно. Но все-таки медимн зерна падает с шумом!

«Куча»
Одна песчинка не есть куча песка. Если n песчинок не есть куча песка, то и n+1 песчинка - тоже не куча. Следовательно, никакое число песчинок не образует кучу песка. К этому парадоксу можно сделать следующий комментарий: метод полной математической индукции нельзя применять, как показывает парадокс, к объёмно неопределённым понятиям, каковым является понятие "куча песка".

«Может ли всемогущий маг создать камень, который не сможет поднять?»
Если не может - значит, он не всемогущий. Если может - значит, всё равно не всемогущий, т.к. он не может поднять это камень. «Равен ли полный стакан пустому?»
Да. Проведем рассуждение. Пусть имеется стакан, наполненный водой до половины. Тогда можно сказать, что стакан, наполовину полный равен стакану, наполовину пустому. Увеличивая обе части равенства вдвое, получим, что стакан полный равен стакану пустому.

«Софизм Кратила»
Диалектик Гераклит, провозгласив тезис "все течет", пояснял, что в одну и ту же реку (образ природы) нельзя войти дважды, ибо когда входящий будет входить в следующий раз, на него будет течь уже другая вода. Его ученик Кратил, сделал из утверждения учителя другие выводы: в одну и ту же реку нельзя войти даже один раз, ибо пока ты входишь, она уже изменится.

«Софизм Эватла»
Эватл брал уроки софистики у софиста Протагора под тем условием, что гонорар он уплатит только в том случае, если выиграет первый процесс. Ученик после обучения не взял на себя ведения какого-либо процесса и потому считал себя вправе не платить гонорара. Учитель грозил подать жалобу в суд, говоря ему следующее: "Судьи или присудят тебя к уплате гонорара или не присудят. В обоих случаях ты должен будешь уплатить. В первом случае в силу приговора судьи, во втором случае в силу нашего договора". На это Эватл отвечал: "Ни в том, ни в другом случае я не заплачу. Если меня присудят к уплате, то я, проиграв первый процесс, не заплачу в силу нашего договора, если же меня не присудят к уплате гонорара, то я не заплачу в силу приговора суда". (Ошибка становится ясной, если мы раздельно поставим два вопроса: 1) должен ли Эватл платить или нет и 2) выполнены ли условия договора или нет.)

Другие примеры софизмов, сформулированных еще в древней Греции:

«Сидящий встал; кто встал, тот стоит; следовательно, сидящий стоит».

«Сократ - человек; человек - не то же самое, что Сократ; значит, Сократ - это нечто иное, чем Сократ».

«Для того чтобы видеть, вовсе необязательно иметь глаза, ведь без правого глаза мы видим, без левого тоже видим; кроме правого и левого, других глаз у нас нет; поэтому ясно, что глаза не являются необходимыми для зрения».

«Тот, кто лжет, говорит о деле, о котором идет речь, или не говорит о нем; если он говорит о деле, он не лжет; если он не говорит о деле, он говорит о чем-то несуществующем, а о нем невозможно не только лгать, но даже мыслить и говорить».

«Если какой-нибудь человек говорит, что он лжет, то лжет ли он или говорит правду?» Допущение того, что он говорит правду, будет означать, что правдой является то, что он лжет (об этом он и говорит), значит, выходит, что лжет. Если же он лжет, то это как раз и есть то, что он открыто признает. Получается, что он говорит правду».


А вот несколько примеров современных софизмов:

«Одна и та же вещь не может иметь какое-то свойство и не иметь его. Хозрасчет предполагает самостоятельность, заинтересованность и ответственность. Заинтересованность — это, очевидно, не ответственность, а ответственность — не самостоятельность. Получается вопреки сказанному вначале, что хозрасчет включает самостоятельность и несамостоятельность, ответственность и безответственность».

«Акционерное общество, получившее когда-то ссуду от государства, те-перь ему уже не должно, так как оно стало иным: в его правлении не осталось никого из тех, кто просил ссуду».

Содержание
1. Введение 3
2. История софизмов 3
3. Классификация софизмов 7
3. 1 Алгебраические софизмы 7
3.2 . Геометрические софизмы 17
3.3 . Логические софизмы 21
4. Классификация ошибок 28
4.1 Терминологические ошибки 28
4.2 Психологические ошибки 29
4.2 .1 Интеллектуальные причины 29
4.2 .2 Аффективные причины 29
4.2 .3 Волевые причины 29
5. Заключение 31
6. Терминологический словарь 32
7. Литература 33

1. Введение

История математики полна неожиданных и интересных софизмов и
парадоксов. И зачастую именно их разрешение служило толчком к новым
открытиям, из которых в свою очередь произрастали новые софизмы и
парадоксы.
В истории развития математики софизмы играли существенную роль. Они
способствовали повышению строгости в математических рассуждениях и
содействовали более глубокому уяснению понятий и методов математики.
Роль софизмов в развитии математики сходна с той ролью, какую играли
непреднамеренные ошибки в математических доказательствах, допускаемые
даже выдающимися математиками.
Большинство софизмов известно очень давно, и можно найти в различных
сборниках, журналах. Некоторые из них передаются устно из поколения в
поколение. Целью моей работы было классифицировать различные виды
софизмов и дать характеристику наиболее часто встречающимся ошибкам.

2. История софизмов

Софизм – (от греческого sophisma , «мастерство, умение, хитрая
выдумка, уловка») умозаключение или рассуждение, обосновывающее
какуюнибудь заведомую нелепость, абсурд или парадоксальное
утверждение, противоречащее общепринятым представлениям. Софизм,
основан на преднамеренном, сознательном нарушении правил логики. Каким
бы ни был софизм, он всегда содержит одну или н е с ко лько
замаскированных ошибок.

Математический софизм – удивительное
утверждение, в доказательстве которого кроются незаметные, а подчас и
довольно тонкие ошибки. История математики полна неожиданных и
интересных софизмов, разрешение которых порой служило толчком к новым
открытиям. Математические софизмы приучают внимательно и настороженно
продвигаться вперед, тщательно следить за точностью формулировок,
правильностью записи чертежей, за законностью математических операций.
Очень часто понимание ошибок в софизме ведет к пониманию м атематики в
целом, помогает разв ивать логику и навыки правильного мышления. Если
нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки
предупреждает от ее повторения в дальнейших математических
рассуждениях.
Пожалуй, особенно поучительна в этом отношении история аксиомы
Евклида о параллельных прямых. Сформулировать эту аксиому можно так:
через данную точку, лежащую вне данной прямой, можно провести не более
одной прямой, параллельной данной (что одну прямую, параллельную

данной, можно провести – это доказывается). Это утверждение на
протяжении более чем двух тысяч лет пытались доказать, вывеси из
остальных аксиом геометрии, но все попытки не увенчались успехом.
Полученные «доказательства» оказались ошибочными. И всё же, несмотря
на ошибочность этих «доказательств», они принесли большую пользу
развитию геометрии. Можно сказать, что они подготовили одно из
величайших достижений в области геометрии и всей математики –
создание неевклидовой геометрии. Честь разработки новой геометрии
принадлежит нашему великому соотечественнику Н.И. Лобачевскому и
венгерскому математику Яношу Бойяи. Н.И. Лобачевский и сам сначала
пытался доказать аксиому параллельных, но скоро понял, что этого
сделать нельзя. И путь, идя которым Лобачевский убедился в этом,
привёл его к созданию новой геометрии. Этот замечательный вклад в
математику был одним из тех, которые прославили русскую науку.
Аристотель называл софизмом «мнимые доказательства», в которых
обоснованность заключения кажущаяся и обязана чисто субъективному
впечатлению, вызванному недостаточностью логического или
семантического анализа. Убедительность на первый взгляд многих
софизмов, их «логичность» обычно связана с хорошо замаскированной
ошибкой — семиотической: за счёт метафоричности речи, омонимии
или полисемии слов, амфиболий и пр., нарушающих однозначность мысли и
приводящих к смешению значений терминов, или же логической: подмена
основной мысли (тезиса) доказательства, принятие ложных посылок за
истинные, несоблюдение допустимых способов рассуждения (правил
логического вывода), использование «неразрешённых» или даже
«запрещённых» правил или действий, например деления на нуль в
математических софизмах
Вот один из древних софизмов («рогатый»), приписываемый Эвбулиду:
«Что ты не терял, то имеешь. Рога ты не терял. Значит, у тебя рога» .
Здесь маскируется двусмысленность большей посылки. Если она мыслится
универсальной: «Всё, что ты не терял…», то вывод логически
безупречен, но неинтересен, поскольку очевидно, что большая посылка
ложна; если же она мыслится частной, то заключение не следует
логически. Последнее, однако, стало известно лишь после того, как
Аристотель сформулировал логику.
А вот современный софизм, обосновывающий, что с возрастом «годы
жизни» не только кажутся, но и на самом деле короче: «Каждый год вашей
жизни — это её 1 / n часть, где n — число прожитых вами
лет. Но n + 1 n . Следовательно, 1 / ( n + 1) Исторически с понятием «софизм» неизменно связывают идею о намеренной
фальсификации, руководствуясь признанием Протагора, что задача софиста
— представить наихудший аргумент как наилучший , путём
хитроумных уловок в речи, в рассуждении, заботясь не об истине, а об
успехе в споре или о практической выгоде. Повидимому, первыми, кто
понял важность семиотического анализа софизмов, были сами софисты.
Учение о речи, о правильном употреблении имён Продик считал важнейшим.
Анализ и примеры софизмов часто

встречаются в диалогах Платона. Аристотель написал специальную книгу
«О софистических опровержениях», а математик Евклид —
«Псевдарий» — своеобразный каталог софизмов в геометрических
доказательствах.
" В Древней Греции развитие искусства ведения дискуссий нередко
приводило к изобретению хитроумных "доказательств" неверных
утверждений. Такие "доказательства" называются софизмами, поскольку их
часто использовали софисты учителя философии и красноречия в Древней
Элладе."
С офистами в древней Греции называли философовучителей, задачей
которых было научить своих учеников «мыслить, говорить и делать».
Будучи в большинстве случаев глубоко образованными людьми, они не
столько передавали ученикам знания из различных областей науки,
сколько стремились научить их владеть искусством словесных состязаний.
Чтобы выйти победителем в словесном поединке, софисты часто
пользовались тем, что противник недостаточно глубоко знает предмет, о
котором идет речь, недостаточно внимателен и наблюдателен , и поэтому
не в состоянии отличить ложь от истины. В результате словесного
поединка противник должен был согласиться с доводами софиста и
признать себя побежденным, хотя истина, казалось, была на его стороне.

3. Классификация софизмов

3.1 Алгебраические софизмы

Алгебра — один из больших разделов математики, принадлежащий
наряду с арифметикой и геометрией к числу старейших ветвей этой науки.
Зада чи, а также методы, отличающие её от других отраслей математики,
создавались постепенно, начиная с древности. Алгебра возникла под
влиянием нужд общественной практики, в результате поисков общих
приёмов для решения однотипных арифметических задач. Приёмы эти
заключаются обычно в составлении и решении уравнений. Т.е.
алгебраические софизмы – намеренно скрытые ошибки в уравнениях и
числовых выражениях.
Примеры софизмов

1. «Число, равное другому числу, одновременно и больше, и меньше
его».
Возьмем два произвольных положительных равных числа a и b и напишем
для них следующие очевидные неравенства:
a b и b b . (1)
Перемножив оба этих неравенства почленно, получим неравенство a · b
b · b , а после его деления на b , что вполне законно, ведь b 0 ,
придем к выводу, что
a b . (2)
Записав же два других столь же бесспорных неравенства
b a и a a , (3)
Аналогично предыдущему получим, что b · a a · a , а разделив на a
0 , придем к неравенству
b a . (4)
Итак, число a , равное числу b , одновременно и больше, и меньше его.

Где ошибка?
Ошибка совершена при переходе от равенства (1) к (2), и от равенства
(3) к (4). Т.к. число b положительное по условию, то – b
отрицательное, следовательно , при перемножении почленно знак нужно
изменить на противоположный, аналогично для a .

2. « Если “ a ” больше “ b ” , то
“ a ” всегда больше, чем “ 2 b b ” »
Возьмем два произвольных положительных числа a и b , такие, что a b
. Умножив это

неравенство на b , получим новое неравенство ab b · b , а отняв от
обеих его частей a · a , получим неравенство ab a · a b · b a · a ,
которое равносильно следующему:
a ( b a ) ( b + a )( b a ) . (1)
После деления о беих частей неравенства (1) на b a получим, что
a b + a (2),
А прибавив к этому неравенству почленно исходное неравенство a b ,
имеем 2 a 2 b + a , откуда
a 2 b .
Итак , если a b , то a 2 b .
Где ошибка?
Ошибка совершена при переходе от равенства (1) к (2). Т.к. a b , то
b a

3. «Отрицательное число больше положительного».
Возьмем два положительных числа а и с. Сравним два отношения:
и
Они равны, так как каждое из них равно – (а/с). Можно составить
пропорцию:
=
Но если в пропорции предыдущий член первого отношения больше
последующего, то предыдущий член второго отношения также больше своего
последующ его. В нашем случае а-с, следо вательно, должно быть
– ас, т.е. отрицательное число больше положительного.
Где ошибка?
Данное свойство пропорции мо жет оказаться неверным, если не которые
члены пропорции отрицательны.

4. «Восемь равно шести»
Р ешим систему двух уравнений
Сделаем это подстановкой у из 2го уравнения в 1, получаем х+8-х=6 ,
откуда
8=6
Где же ошибка?
Уравнение (2) можно записать как х+2у =8, так что исходная система за
пишется в виде
В этой системе уравнений коэффициенты при переменных одинаковы, а
правые части не равны между собой, из этого следует, что система
несовместна, т.е. не имеет ни одного решения. Графически это означает,
что прямые у=3и у=4параллельны и не совпадают. Перед тем, Как решать
систему линейных уравнений, полезно проанализировать, имеет ли система
единственное решение, бесконечно много решений или не имеет решений
вообще.

5. «Единица равна двум»
Простым вычитанием легко убедиться в справедливости равенства
1-3=4-6
Добавив к обеим частям этого равенства число , получим новое
равенство
1-3 + =4-6 +
в котором, как нетрудно заметить, правая и левая части представляют
собой полные квадраты, т.е .
2 = 2 (1)
Извлекая из правой и левой частей предыдущего равенства квадратный
корень, получаем равенство
1= 2(2)
Откуда следует, что
1=2
Где ошибка?
Неправильное извлечение корня из квадрата числа в переходе от
равенства (1) к (2).

6. «Все числа равны»
Возьмём два разных числа, такие что: a Тогда существует такое c 0 , что: a + c = b
Умножим обе части на ( a −'3f b ) , имеем: ( a + c )( a
−'3f b ) = b ( a −'3f b )
Раскрываем скобки, имеем: a 2 + ca −'3f ab −'3f cb = ba
−'3f b 2
cb переносим вправо, имеем: a 2 + ca −'3f ab = ba −'3f
b 2 + cb
a ( a + c −'3f b ) = b ( a −'3f b + c )
a = b
Где ошибка?
По определению : a + c = b
Значит, a + c −'3f b = 0
И выражение a ( a + c −'3f b ) = b ( a + c −'3f b )
Тождественно a ∙'95 0 = b ∙'95 0 .

7. Дваж ды два пять!

Возьмем в качестве исходного соотношения следующее очевидное
равенство:
4:4= 5:5 (1) .
После вынесения за скобки общего множителя из каждой части равенства
(1) будем иметь:
4∙'95 (1:1)=5 ∙'95 (1:1) (2)
или
(2∙'952)(1:1)=5 (1:1) (3)
Наконец, зная, что 1:1=1, мы из соотношения (2) устанавливаем:
2 ∙'95 2=5.
Где ошибка?
Нельзя выносить множитель за скобки, как это сделано в равенстве (2).

8. «Неравные числа равны»
Возьмём два неравных между собой произвольных числа a и b . Пусть их
разность равна c , т.е. a b = c . Умножив обе части этого равенства на
( a b ) , получим:
( a b ) 2 = c ( a b )
раскрыв скобки, придем к равенству
a 2 -2 ab + b 2 = ca cb
Преобразованием получаем
a 2 -abac = abb 2 -bc
Вынося общий множитель а слева, и общий множитель b справа получим
a(ab-c) = b(ab-c)
Разделив последнее равенство на ( a b c ), получаем
a = b
Где ошибка?
Здесь ошибка совершена при переходе от равенства a ( a b c ) = b ( a
b c ) к равенству, а = b . Действительно, согласно условию разность
двух произвольных чисел а и b равна с, т. е. аb = с , откуда аb-с = 0
. Можно записать равенство a ( a b c ) = b ( a b c ) в виде: а*0= b*0
. Переход от этого равенства к равенству, а = b осуществляется путем
деления обеих частей на равное нулю число аb-с = 0 . Следовательно,
здесь мы имеем деление нуля на нуль, которое не имеет смысла,
поскольку равенство, а*0 = b*0 выполняется при любых а и b . Поэтому
вывод, сделанный в софизме, что числа а и b равны, неверен.

9. «Любое число равно нулю»
Возьмем произвольное положительное число а и рассмотрим сумму х
бесконечного числа слагаемых, равных а:
х=а+а+а+а+… .
Очевидно, что мы можем представить эту сумму как
х=а+(а+а+а+….)
в которой сумма, стоящая в скобках, также равна х как сумма
бесконечного числа слагаемых, равных а. Так что можем записать, что
х=а+х, откуда заключаем, что
а=0
Где ошибка?
Ошибка допущена в равенстве (1) , в котором бесконечная сумма чисел а
обозначена конечным числом х .

1 0 . «Единица равна нулю»
Возьмем уравнение
x a =0
Разделив обе его части на ха, получим
=
Откуда сразу же получаем требуемое равенство
1=0
Где ошибка?
Ошибка заключается в деление на нуль.

1 1 . Любое число равно
Возьмем два произвольных положительных действительных и равных друг
другу числа x и z . Поскольку по условию x = z , то . Поэтому с полным
основанием мы можем записать два следующих тождества
х= z (1)
(2)
Сложив эти два неравенства почленно, получим
(3)
Прибавив и отняв в левой части равенства (3) величину вместо
равенства(3) получим, или, что очевидно, то же самое,
(4)
В левой части последнего равенства первый и второй члены представим в
виде , а третий и четвертый в виде . В результате этих преобразований
равенство (4) примет вид
= (5)
И окончательно может быть записано так:
(6)
Для того чтобы равенство (6) имело место, необходимо выполнения
условия
(7)
А так как в силу исходного равенства x = z , заключаем, что 2 , или , откуда
x=
Где ошибка?
В этом софизме все выкладки вплоть до равенства (6) проведены
правильно. Ошибка содержится при переходе от равенства (6) к равенству
(7).
Действительно, каково бы ни было число а , произведение а на нуль
всегда дает нуль. Другими словами, в равенстве а ∙'95 0=0число
а может быть каким угодно.
По условию числа x и z равны между собой. Следовательно, равны и их
арифметическ ие квадратные корни , т.е. , а поэтому и т аким образом,
равенство(6) можно записать в виде , откуда сразу же следует, что
число может иметь вообще любое значение.

1 2 . «Неравные числа равны»
Возьмем два неравных между собой произвольных числа а и b . Пусть их
разность равна с , т.е. аb = c
Умножив обе части этого равенства на аb , получим (аb ) 2 = c ( a b )
, а раскрыв скобки, придем к равенству a 2 -2 ab + b 2 = ca cb , из
которого следует равенство a 2 ab ac = ab b 2 bc . Вынося общий
множитель а слева и общий множитель b справа за скобки получим:
a ( a b c )= b ( a b c ) (1)
Разделив последнее равенство на ( a b c ) , получаем, что
a = b
Где ошибка?
Т. к. аb = c , то a b c =0, следовательно, ошибка заключается в
деление на 0.

13. « Всякое число равно своему удвоенному значению»
Запишем очевидное для любого числа а тождество
а 2 -а 2 = а 2 -а 2
Вынесем а в левой части за скобку, а правую часть разложим на
множители по формуле разности квадратов, получив:
а(аа)=(а+а)(аа) (1)
Разделив обе части на аа, получим а=а+а , или
а=2а
Где ошибка?
Т.к. аа=0 , то ошибка заключается в деление на нуль равенства (1).

14. «Единица равна минус единице»
П усть число х равно 1. Тогда можно записать, что х 2 =1 , или х 2
-1=0 . Р аскладывая х 2 -1 по формуле разности квадратов, получим:
(х-1)(х+1)=0 (1)
Разделив обе части этого равенства на х-1 , имеем:
х+1=0 и х = -1 (2)
Поскольку по условию х=1 , то отсюда приходим к равенству
1= -1
Где ошибка?
Ошибка аналогична ошибке в примере 13.

15. « Если одно число больше другого, то эти числа равны»
Возьмем два произвольных числа т и п , такие, что т п , и другие три
произвольных числа а, b и с , сумма которых равна d , т.е. а+ b + c =
d .
Умножив обе части этого равенства на т , а затем на п , получим:
ma+mb+mc=md, na+nb+nc=nd
Сложив почленно равенства
ma + mb + mc = md
nd = na + nb + nc
получим ma + mb + mc + nd = na + nc + nb + md . Перенося здесь nd
вправо , а md влево, имеем
ma+mb+mcmd=na+nb+ncnd
Вынося слева число т , а справа число п за скобки, придем к
соотношению
m(a+b+cd)=n(a+b+cd) , (1)
Разделив обе части последнего равенства на ( a + b + c d ) , находим,
что
т=п
Где ошибка?
Ошибка аналогична ошибке в примерах 13 и 14.

16. «Семь равно тринадцати»
Р ассмотрим уравнение
(1)
Оно может быть решено следующим образом. Приведя левую часть
уравнения к общему знаменателю, будем иметь , откуда , или
(2)
Поскольку числители дробей в левой и правой частях уравнения равны, то, для того чтобы имело место равенство обеих частей
уравнения, необходимо, чтобы были равны и знаменатели дробей. Таким
образом, приходим к равенству.
7=13
Где ошибка?
Область допустимых значений исходного уравнения (1) состоит из всех
значений переменой х кроме х=7, х=13. В этом софизме неявно
подразумевается, что равенство(2) является не уравнением, а тождеством
равным при любых значениях х, что неверно. Поэтому утверждение софизма
не имеет места.

17. «Сумма любых двух чисел равна их полусумме»
Возьмем два произвольных числа а и b и возведем их сумм у в степень п
. Воспользуемся для этого формулой бинома Ньютона:
с праведливой для любого натурального числа п .
Положив в формуле бинома Ньютона п=2т , получим
(1)
Приняв в последнем соотношении т = и учитывая, что а 0 =1 и b 0 =1 ,
найдем, что
( a + b ) 1 = a + b +0+ ... +0+ a + b . (2)
Откуда получаем равенство a + b =2 a +2 b , или
a + b =
Где ошибка?
Известно, что в формуле бинома Ньютона для (а+ b ) n число членов его
разложения равно n +1. Недоразумение возникло потому, что в формуле
(1) выписано в общем виде три первых члена, три последних и
промежуточные члены, замененные многоточием. В формуле (1) должно было
остаться только первые два слагаемых. Т.е. (а+ b) 1 =a+b

18. «Половина любого числа равна половине ему противоположного»

Возьмем произвольное число а и положим . Тогда 2х+а=0 или после
умножения на а получим 2ах+а 2 =0 . Прибавляя к обеим частям этого
равенства х 2 , имеем:
х 2 +2ах+а 2 =х 2 .
Так как х 2 +2ах+а 2 = (х+а) 2 , то предыдущее равенство можно
записать в виде
(х+а) 2 = х 2 , (1)
а после извлечения квадратного корня из обеих частей последнего
равенства получаем
х+а= х. (2)
Поскольку по условию , то из равенства (2) имеем , и поэтому получаем
окончательно
Где ошибка?
Ошибка состоит в неправильном извлечении квадратного корня из
квадрата числа.

19. «Любое положительное число равно числу, ему противоположному»

Возьмем произвольное положительное число z . По правилам извлечения
квадратных корней имеем
(1)
С другой стороны,
(2)
Отсюда получаем, что
z =z
Где ошибка ?
Ошибочна последовательность равенств (2). Т.к. z положительное, то
– z – отрицательное, тогда не имеет смысла.

3 . 2 . Геометрические софизмы

Геометрические софизмы – это умозаключения или рассуждения,
обосновывающие какуюнибудь заведомую нелепость, абсурд или
парадоксальное утверждение, связанное с геометрическими фигурами и
действиями над ними.
Примеры геометрических софизмов

1. «Катет равен гипотенузе»
Угол С равен 90 ˚'3f , ВД биссектриса угла СВА, СК = КА, ОК
перпендикулярна СА, О точка пересечения прямых ОК и ВД, ОМ
перпендикулярна АВ, ОL перпендикулярна ВС. Имеем: треугольник LВО
равен треугольнику МВО, ВL = ВМ, ОМ = ОL = СК = КА, треугольник КОА
равен треугольнику ОМА (ОА общая сторона, КА = ОМ, угол ОКА и угол ОМА
прямые), угол ОАК = углу МОА, ОК = МА = СL, ВА = ВМ + МА,

ВС = ВL + LС, но ВМ = ВL, МА = СL, и потому ВА = ВС.
2
Ошибка заключается в том, что рассуждения, о том, что катет равен
гипотенузе, опирались на ошибочный чертеж. Точка пересечения прямой,
определяемой биссектрисой ВD и серединного перпендикуляра к катету АС,
находится вне треугольника АВС.
2.
Рассмотрим произвольный треугольник АВС, в котором р и q –
проекции сторон АВ и АС на сторону ВС соответственно, h – высота
треугольника, опущенная из вершины А.
Проведем параллельно высоте h отрезок ED , делящий треугольник АВС на
две равновеликие части, причем ED = h ' . Обозначим через х отрезок на
стороне ВС от вершины В до основания перпендикуляра h ' , т.е. до
точки D .
Условие равенства площадей двух равновеликих частей треугольника АВС
, лежащих слева и справа от прямой h ' , приводит к соотношению
(1)
Поскольку треугольники BED и BAF подобны по признаку подобия
прямоугольных треугольников, то справедливо равенство , откуда
.
Подставляя последнее равенство в (1) получим , откуда
.
Поскольку точки В и С равноправны, то аналогично предыдущему получим,
что
где у – отрезок стороны ВС от вершины С до основания h ' . Так
как х+у=р+ q , то, подставляя вместо х и у полученные для них
выражения и деля обе части этого равенства на , получим
откуда
Где ошибка?
Точки В и С не равноправны. Если поменять местами эти точки,
поменяется и система обозначений, которая используется для получения
формул (1) и (2) . В софизме через х обозначен отрезок на стороне ВС
от вершины В до основания h ' т.е. до точки D , причем расстояние BD ,
равное х, является катетом прямоугольного треугольника BDE . Поменяв
же местами обозначения вершин В и С , получим что х теперь не будет
катетом треугольника BDE . Вместо него катетом будет служить отрезок
СВ, обозначенный как у. Эти действия приводят к переобозначению х на у
и подмене истинной формулы для у на неверную формулу (3).

3. « Отрезки параллельных прямых, заключенные между сторонами
угла, равны»
Рассмотрим произвольный угол с вершиной в точке Е и пересечем их
стороны двумя параллельными прямыми, отрезки которых АВ и CD заключены
между сторонами этого угла.
Как известно параллельные прямы отсекают от сторон угла
пропорциональные отрезки, следовательно, , откуда
АЕ· DE = BE · CE
Умножив обе части последнего равенства на отличную от нуля разность
АВ – CD , запишем
AE·DE·AB AE·DE·CD = AE·DE·CD BE·CE·CD,
Или
AB(AE·DE BE·CE) = CD(AE·DE BE·CE)
Разделив обе части последнего равенства на ( AE · DE BE · CE )
получим равенство
АВ= CD
Где ошибка ?
Т.к. АЕ· DE = BE · CE , то AE · DE BE · CE = 0, то ошибка в деление
на 0.

4. «Внешний угол треугольника равен внутреннему, не смежному с
ним»
Рассмотрим четырехугольник ABCD , такой, в котором
ADC + ABC =180˚'3f
Через точки A , D и С проведем окружность, которая пересечет стороны
АВ и ВС в некоторых точках E и F . Соединив точки С и Е, получим
вписанный в эту окружность четырехугольник ADCE . Но

сумма противоположных углов всякого вписанного четырехугольника , как
известно, равна 180˚'3f , потому
ADC + AEC = 180˚'3f
Сравнив равенства (1) и (2), получим ADC + ABC = ADC + AEC
ABC = AEC
2
Где ош ибка?
Ошибка кроется в том, что на самом деле окружность, проведена через
точки А, D и С данного четырехугольника, обязательно пройдет через
точку B . Другими словами, все точки четырехугольника ABCD должны
лежать на одной окружности.
По условию четырехугольник ABCD построен так, что углы при вершинах В
и D в сумме составляют 180 ˚'3f . Но это условие является
условием того, что вокруг этого четырехугольника можно описать
окружность.

5. «Из точки на прямую можно опустить два перпендикуляра»
Попытаемся доказать, что через точку, лежащую вне прямой, к этой
прямой можно провести два перпендикуляра. С этой целью возьмем
∆'3fАВС. На сторонах АВ и ВС этого треугольника, как на
диаметрах, построим полуокружности. Пусть эти полуокружности
пересекаются со стороной АС в точках Е и D . Соединим точки Е и D
прямыми с точкой В. Угол АЕВ – прямой, как вписанный,
опирающийся на диаметр, угол В DC также прямой. Следовательно,
ВЕ║'a6АС и В D ║'a6АС. Через точку В проходят два
перпендикуляра к прямой АС.
Где ошибка?
Рассуждения опирались на ошибочный чертеж. В действительности
полуокружности пересекаются со стороной АС в одной точке, т.е. ВЕ
совпадает с В D .
Даже если чертеж был бы правильным, то не возможно, что в
треугольнике ВЕ D сумма всех углов больше 180 ˚'3f . ( Е=90
˚'3f , D =90 ˚'3f ).

6. «Хорда, не проходящая через центр окружности , равна диаметру»

Пусть в окружности приведен диаметр АВ. Через точку В проведем
какуюлибо хорду ВС, не проходящую через центр, затем через середину
этой хорды D и точку А проведем новую хорду АЕ. Наконец, точки Е и С
соединим отрезком прямой. Рассмотрим ∆'3f АВ D и ∆'3f Е
D С. В этих треугольниках: В D = DC (по построению), А= С (как
вписанные, опирающиеся на одну и ту же дугу). Кроме того, В D А= Е DC
(как вертикальные). Если же сторона и два угла одного треугольника
соответственно равны
стороне и двум углам другого треугольника, то такие треугольники
равны.
Значит, ∆'3f В D А= ∆'3f Е DC , а в равных
треугольниках против равных углов лежат равные стороны. Поэтому,
АВ=ЕС.
2
Где ошибка?
По теореме о признаке равенства треугольника:
Если сторона и два прилежащих к ней угла одного треугольника
соответственно равны стороне и двум прилежащим к ней углам другого
треугольника, то такие треугольники равны.
А в нашем случае, А не прилежит к стороне В D .

7. «Все треугольники равнобедренные»
Докажем, что все треугольники –
равнобедренные.
Рассмотрим произвольный треугольник АВС (рис.). Проведем в нем
биссектрису угла В и серединный перпендикуляр к стороне АС . Точку их
пересечения обозначим через О . Из точки О опустим перпендикуляр О D
на сторону АВ и перпендикуляр ОЕ на сторону

ВС . Очевидно, что
ОА=ОС и О D =ОЕ . Но тогда прямоугольные треугольники АО D и СОЕ
равны по катету и гипотенузе.
Поэтому D АО = ЕС О . В то же время ОАС= ОСА, так как треугольник АОС
равнобедренный. Получаем: ВАС= D АО+ ОАС= ЕС О + ОСА= В СА
Итак, угол ВАС равен углу ВСА , поэтому треугольник АВС
равнобедренный: АВ=ВС .
2
Где ошибка?
Здесь ошибка в чертеже. Серединный перпендикуляр к стороне и
биссектриса противоположного ей угла для неравнобедренного
треугольника, пересекаются вне этого треугольника.

8. «Куда пропала клетка?»
И еще один пример софизма. Посмотрим на рисунок. Прямоугольники явно
равносоставлены, но площадь одного равна 64 клеткам, а площадь
другого65.
И здесь ошибка в чертеже .Точки В, Е, F и D не лежат на одной прямой,
а являются вершинами очень узкого параллелограмма, площадь которого
равна площади одной клеткитой самой лишней клетки.
9. «Все хорды одной и той же окружности равны»
Возьмем две произвольные неравные хорды одной произвольной окружности
и проведем соответственно равные им и параллельные между собой хорды
АВ и CD . Пусть S – точка пересечения продолжений отрезков АС и
BD .
Поскольку треугольники SAB и SCD подобны, то имеет место пропорция
, откуда
AB · SC = CD · AS
Умножая почленно последнее равенство на отличную от нуля величину CD
AB , получим
AB·SC·CD AB 2 ·SC = AS·CD 2 AB·AS·CD,
или
AB·SC·CD AS·CD 2 = AB 2 ·SC AB·AS·CD
а после вынесения общего множителя в левой и правой частях получим
CD(AB·SC AS·CD) = AB (AB·SC AS·CD)
Сокращая последнее равенство на общий множитель, получим
окончательное равенство
CD = AB
Где ошибка?
Т . к . AB ·SC=CD·AS, то AB·SC AS·CD=0. Т.е ошибка в деление на 0.

3.4. Логические софизмы

Кроме математических софизмов, существует множество других. Понять
абсурдность таких утверждений проще, но от этого они не становятся
менее интересными. Очень многие софизмы выглядят как лишенная смысла и
цели игра с языком; игра, опирающаяся на многозначность языковых
выражений, их неполноту, недосказанность, зависимость их значений от
контекста и т.д. Эти софизмы кажутся особенно наивными и несерьезными.

Примеры логических софизмов

1. «Полупустое и полуполное»
«Полупустое есть то же, что и полуполное. Если равны половины,
значит, равны и целые. Следовательно, пустое есть то же, что и
полное».

2. «Чётное и нечётное»
«5 есть 2 + 3 («два и три»). Два — число чётное, три —
нечётное, выходит, что пять — число и чётное и нечётное. Пять не
делится на два, также как и 2 + 3, значит, оба числа не чётные!»

3. «Не знаешь то, что знаешь»
«Знаешь ли ты, о чём я хочу тебя спросить?» — «Нет». —
«Знаешь ли ты, что добродетель есть добро?» — «Знаю». —
«Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что
знаешь».

4. «Лекарства»
«Лекарство, принимаемое больным, есть добро. Чем больше делать добра,
тем лучше. Значит, лекарств нужно принимать как можно
больше».

5. «Вор»
«Вор не желает приобрести ничего дурного. Приобретение хорошего есть
дело хорошее. Следовательно, вор желает хорошего».

6. «Отец — собака»
«Эта собака имеет детей, значит, она — отец. Но это твоя
собака. Значит, она твой отец. Ты её бьёшь, значит, ты бьёшь своего
отца и ты — брат щенят».

7. «Рогатый»
«Что ты не терял, то имеешь. Рога ты не терял. Значит, у тебя рога».

8. «Самое быстрое существо не способно догнать самое
медленное»
Быстроногий Ахиллес никогда не настигнет медлительную черепаху. Пока
Ахиллес добежит до черепахи, она продвинется немного вперед. Он быстро
преодолеет и это расстояние, но черепаха уйдет еще чуточку вперед. И
так до бесконечности. Всякий раз, когда Ахиллес будет достигать места,
где была перед этим черепаха, она будет оказываться хотя бы немного,
но впереди.

9. «Нет конца»
Движущийся предмет должен дойти до половины своего пути прежде, чем
он достигнет его конца. Затем он должен пройти половину оставшейся
половины, затем половину этой четвертой части и т.д. до бесконечности.
Предмет будет постоянно приближаться к конечной точке, но так никогда
ее не достигнет.

10. «Медимн зерна»
Большая масса мелких, просяных например, зерен при падении на землю
всегда производит шум. Он складывается из шума отдельных зерен, и,
значит, каждое зерно и каждая малейшая часть зерна должны, падая,
производить шум. Однако отдельное зерно падает на землю совершенно
бесшумно. Значит, и падающий на землю медимн зерна не должен был бы
производить шум, ведь он состоит из множества зерен, каждое из которых
падает бесшумно. Но все-таки медимн зерна падает с шумом!

11. «Куча»
Одна песчинка не есть куча песка. Если n песчинок не есть куча песка,
то и n+1 песчинка тоже не куча. Следовательно, никакое число песчинок
не образует кучу песка. К этому парадоксу можно сделать следующий
комментарий: метод полной математической индукции нельзя применять,
как показывает парадокс, к объёмно неопределённым понятиям, каковым
является понятие "куча песка".

12. «Может ли всемогущий маг создать камень, который не сможет
поднять?»
Если не может значит, он не всемогущий. Если может значит, всё равно
не всемогущий, т.к. он не может поднять это камень.

13. «Равен ли полный стакан пустому?»
Да. Проведем рассуждение. Пусть имеется стакан, наполненный водой до
половины. Тогда можно сказать, что стакан, наполовину полный равен
стакану, наполовину пустому. Увеличивая обе части равенства вдвое,
получим, что стакан полный равен стакану пустому.

14. «Софизм Кратила»
Диалектик Гераклит, провозгласив тезис "все течет", пояснял, что в
одну и ту же реку (образ природы) нельзя войти дважды, ибо когда
входящий будет входить в следующий раз, на него будет течь уже другая
вода. Его ученик Кратил, сделал из утверждения учителя другие выводы:
в одну и ту же реку нельзя войти даже один раз, ибо пока ты входишь,
она уже изменится

15. «Софизм Эватла»

Эватл брал уроки софистики у софиста Протагора под тем условием, что
гонорар он уплатит только в том случае, если выиграет первый процесс.
Ученик после обучения не взял на себя ведения какоголибо процесса и
потому считал себя вправе не платить гонорара. Учитель грозил подать
жалобу в суд, говоря ему следующее: "Судьи или присудят тебя к уплате
гонорара или не присудят. В обоих случаях ты должен будешь уплатить. В
первом случае в силу приговора судьи, во втором случае в силу нашего
договора". На это Эватл отвечал: "Ни в том, ни в другом случае я не
заплачу. Если меня присудят к уплате, то я, проиграв первый процесс,
не заплачу в силу нашего договора, если же меня не присудят к уплате
гонорара, то я не заплачу в силу приговора суда". (Ошибка становится
ясной, если мы раздельно поставим два вопроса: 1) должен ли Эватл
платить или нет и 2) выполнены ли условия договора или нет.)

4. Классификация ошибок

4.1 Терминологические ошибки
Грамматические, терминологические и риторические источники софизмов
выражаются
· в неточном или неправильном словоупотреблении и построении фразы
наиболее характерные:
1. Ошибка омонимия. Например: реакция в смысле химическом,
биологическом и историческом; доктор как врач и как учёная степень.
2.Ошибка сложения — когда разделительному термину придаётся
значение собирательного. Все углы треугольника

4.2 Психологические ошибки
Психологические причины софизмов бывают троякого рода:
интеллектуальные, аффективные и волевые. Во всяком обмене мыслей
предполагается взаимодействие между 2 лицами, читателем и автором или
лектором и слушателем, или двумя спорящими. Убедительность софизмов
предполагает два фактора: б — психические свойства одной и в
— другой из обменивающихся мы слями сторон. Правдоподобность
софизмов зависит от ловкости того, кто защищает его, и уступчивости
оппонента, а эти свойства зависят от различных особенностей обеих
индивидуальностей.

4.2 .1 Интеллектуальные причины
Интеллектуальные причины софизма заключаются в преобладании в уме
лица, поддаю щегося софизму, ассоциаций по смежности над ассоциациями
по сходству, в невнимание, в слабой памяти, непривычке к точному
словоупотреблению, бедности знаний по данному предмету, лености в мыш
лении и т.д. Обратные качества, разумеется, являются наиболее выг
одными для лица, защищающего софизм. О бозначим первые отрицательные
качества через b , вторые соответствующие им положительные через a
.
4.2 .2 Аффективные причины
Сюда относятся трусость в мышлении — боязнь опасных
практических последствий, вытекающих от принятия известного положения;
надежда найти факты, подтверждающие ценные для нас взгляды,
побуждающая нас видеть эти факты там, где их нет, любовь и ненависть,
прочно ассоциировавшиеся с известными представлениями, и т.д. Желающий
обольстить ум своего соперника софист должен быть не только искусным
диалектиком, но и знатоком человеческого сердца, умеющим виртуозно
распоряжаться чужими страстями для своих целей. Обозначим аффективный элемент в душе
искусного диалектика, который распоряжается им как актёр, чтобы
тронуть противника, через c , а те страсти, которые пробуждаются в
душе его жертвы и омрачают в ней ясность мышления через d .

4.2 .3 Волевые причины
При обмене мнений мы воздействуем не только на ум и чувства
собеседника, но и на его волю. Во всякой аргументации (особенно
устной) есть элемент внушения. Категоричность тона, не допускающего
возражения, определённая мимика и т. п. ( e ) действуют на лиц, легко
поддающихся внушению, особенно на массы. С другой стороны, пассивность
( f ) слушателя особенно благоприятствует успешности аргументации
противника. Таким образом, всякий С. предполагает взаимоотношение
между шестью психическими факторами: a + b + c + d + e + f .
Успешность С. определяется величиной этой суммы, в которой a + c + e
составляет показатель силы диалектика, b + d + f есть показатель
слабости его жертвы. Прекрасный психологический анализ софистики даёт
Шопенгауэр в своей «Эристике» (перев. кн. Д. Н. Цертелева).

5. Заключение

Поиск заключенных в софизме ошибок, ясное понимание их причин
ведет к осмысленному изучению математики. Обнаружение и анализ
ошибки, заключенной в софизме, очень часто оказывается более
поучительным, чем просто разбор решений «безошибочных» задач.
Эффектная демонстрация «доказательства» явно неверного результата,
демонстрация того, к какой нелепице приводит пренебрежение какимлибо
математическим правилом, и последующий поиск и разбор ошибки,
позволяют понять и «закрепить» математическое правило или утверждение.
Такой подход способствует пониманию того , что математика – это
живая наука, а не собрание закостенелых догм, выдуманных по чьейто
злой воле.

6. Терминологический словарь
Амфиболимя (греч. ἀ'3f мцйвплЯб — двусмысленность,
неясность) — двойственность или двусмысленность,
получающаяся от того или иного расположения слов или от употребления
их в различных смыслах, смешение понятий.
Омонимы — разные по значению, но одинаковые по написанию и
звучанию единицы языка (слова, морфемы и др.). Термин введён
Аристотелем.
Полисемия (от греч. рплхузмеЯб — « многозначный») —
многозначность, наличие у слова (единицы языка) двух или более
взаимосвязанных и исторически обусловленных значений.
Простой категорический силлогизм — рассуждение, состоящее из
трёх простых атрибутивных высказываний: двух посылок и одного
заключения. Посылки силлогизма разделяются на большую (которая
содержит предикат заключения) и меньшую (которая содержит субъект
заключения). По положению среднего термина силлогизмы делятся на
фигуры, а последние по логической форме посылок и заключения —
на модусы.
Пример силлогизма:
Всякий человек смертен ( большая посылка)
Сократ — человек (меньшая посылка)
-----------Сократ смертен (заключение)

6. Литература
1. Lietzman W. Wo steckt
der Fehler? Mathematische Trugschlьsse und Warnzeichen. –
Leipzig? 1952
2. Аменицкий Н. Математические развлечения и любопытные приемы
мышления. – М., 1912
3. Богомолов С. А. Актуальная бесконечность. – М.; Л., 1934
4. Больцано Б. Парадоксы бесконечного. – Одесса, 1911
5. Брадис В. М., Харчева А. К. Ошибки в математических рассуждениях.
– М., 1938
6. Горячев Д. Н., Воронец А. М. Задачи, вопросы и софизмы для
любителей математики. – М., 1903
7. Литцман В., Трир Ф. Где ошибка? – СПб., 1919
8. Лямин А. А. Математические парадоксы и интересные задачи. –
М., 1911
9. Мадера А.Г., Мадера Д.А. Математические софизмы. – М.:
Просвещение, 2003
10. Обреимов В. И. Математические софизмы. – 2-е изд. –
СПб., 1889.