Формирование математической функциональной грамотности у младших школьников

Министерство просвещения Российской Федерации

Нижнетагильский государственный социально-педагогический институт (филиал) федерального государственного автономного образовательного учреждения высшего образования

«Российский государственный профессионально-педагогический университет»

Факультет психолого-педагогического образования

Кафедра психологии и педагогики дошкольного и начального образования

ФОРМИРОВАНИЕ МАТЕМАТИЧЕСКОЙ ФУНКЦИОНАЛЬНОЙ ГРАМОТНОСТИ У МЛАДШИХ ШКОЛЬНИКОВ

Выпускная квалификационная работа

по направлению подготовки 44.03.02 Психолого-педагогическое образование

профилю подготовки «Психология и педагогика начального образования»

Нижний Тагил 2022

Министерство просвещения Российской Федерации

Нижнетагильский государственный социально-педагогический институт (филиал) федерального государственного автономного образовательного учреждения высшего образования

«Российский государственный профессионально-педагогический университет»

Факультет психолого-педагогического образования

Кафедра психологии и педагогики дошкольного и начального образования

Работа допущена к защите Зав. кафедрой ППО _______/Е. В. Малеева/ «04» февраля 2022 г.

Выпускная квалификационная работа

ФОРМИРОВАНИЕ МАТЕМАТИЧЕСКОЙ ФУНКЦИОНАЛЬНОЙ ГРАМОТНОСТИ У МЛАДШИХ ШКОЛЬНИКОВ

Направление подготовки 44.03.02 Психолого-педагогическое образование,

профиль «Психология и педагогика начального образования»

Исполнитель: студентка группы Нт-505 ПСНО	________________ /подпись/	Колногорова Ксения Дмитриевна
Руководитель: доцент кафедры ППО	_________________ /подпись/	Зубарева Е. С., кандидат педагогических наук
Рецензент: доцент кафедры ППО	__________________ /подпись/	Ломаева М.В., кандидат педагогических наук
Нормоконтролер: доцент кафедры ППО	__________________ /подпись/	Зубарева Е. С., кандидат педагогических наук

Нижний Тагил 2022

Министерство просвещения Российской Федерации

Нижнетагильский государственный социально-педагогический институт (филиал) федерального государственного автономного образовательного учреждения высшего образования

«Российский государственный профессионально-педагогический университет»

Факультет психолого-педагогического образования

Кафедра психологии и педагогики дошкольного и начального образования

УТВЕРЖДАЮ:

Зав. кафедрой ППО

________ Е. В. Малеева

ЗАДАНИЕ

на подготовку выпускной квалификационной работы

Студентки Нт-505 ПСНО группы Колногоровой Ксении Дмитриевны.

Направление: 44.03.02 Психолого-педагогическое образование.

Профиль: «Психология и педагогика начального образования».

Руководитель ВКР: Зубарева Елена Сергеевна, кандидат педагогических наук, доцент кафедры психологии и педагогики дошкольного и начального образования филиала РГППУ в городе Нижнем Тагиле.

Срок выполнения ВКР: с 10.11.2021 г. по 13.03.2022 г.

Тема ВКР: «Формирование математической функциональной грамотности у младших школьников».

Утверждена: Протокол заседания кафедры № 2 от 15.10.2021 года. Приказ по НТГСПИ (ф) РГППУ № 822-У от 10.11.2021 г.

Перечень основных теоретических вопросов, подлежащих разработке в данной ВКР: сущность и содержание понятия «математическая функциональная грамотность», её признаки, структура и уровни развития; особенности формирования математической функциональной грамотности у младших школьников; характеристика приёмов, направленных на формирования математической функциональной грамотности младших школьников.

Содержание практической части ВКР (исследовательские материалы, иллюстрированное приложение, творческие работы и т.д.): описание методик и результатов диагностики уровня сформированности математической функциональной грамотности у детей младшего школьного возраста; педагогический проект формирования математической функциональной грамотности у младших школьников.

Основная литература и исходные данные к работе: психологии школьников, возрастным особенностям развития в том числе детей младшего школьного возраста посвящены фундаментальные труды ученых Л. С. Выготского, Д. Б. Эльконина; вопросами изучения функциональной грамотности школьников занимались ученые И. В. Семенова, М. А. Ушакова, К. Т. Медеубаева, М. И. Козлова; функциональной грамотности младшего школьного возраста посвятили свои труды Н. Ф. Виноградова и А. Е. Жумабаева; работы Н. М. Евтыховой, Л. Л. Баговой, А. П. Карачевцевой посвящены математической функциональной грамотности младшеклассников.

План-график выполнения ВКР

Этапы выполнения ВКР	Сроки их выполнения	Подпись руководителя
Ознакомление с положением о подготовке и защите ВКР, программой ИГА	08.11.2021 г.
Написание заявления о выборе темы ВКР	08.11.2021 г.
Составление плана работы по написанию ВКР (совместно с руководителем)	до 17.11.2021 г.
Представление списка использованной литературы и источников	до 27.11.2021 г.
Разработка и согласование с руководителем введения ВКР	до 10.12.2021 г.
Разработка и согласование с руководителем первой главы ВКР	до 24.12.2021 г.
Разработка и согласование с руководителем второй главы ВКР	до 19.01.2022 г.
Разработка и согласование с руководителем заключения ВКР	до 26.01.2022 г.
Оформление текста ВКР	до 03.02.2022 г.
Проведение предварительной защиты ВКР	04.02.2022 г.
Устранение замечаний после предварительной защиты ВКР	до 28.02.2022 г.
Проверка текста ВКР на объем заимствований (научным руководителем)	до 4.03.2022 г.
Прохождение нормоконтроля ВКР	1.03.2022 г.
Представление ВКР рецензенту для написания рецензии	4-13.03.2022 г.
Представление ВКР руководителю для написания отзыва	до 4.03.2022 г.
Составление реестра ВКР	до 13.03.2022 г.
Представление ВКР в ГЭК (секретарю ГЭК)	14.03.2022 г.
Защита выпускной квалификационной работы	18.03.2022 г.

Задание получил:				/Колногорова К.Д./		10.11.2021 г.
	(подпись студента)			(Фамилия И. О. студента)		(дата)
Решением кафедры психологии и педагогики дошкольного и начального образования от 04.02.2022 г., протокол № 6, выпускная квалификационная
работа студентки		Колногоровой Ксении Дмитриевны
		(Фамилия И. О. студента)

признана завершенной и допущена к защите в государственной экзаменационной комиссии (ГЭК).

Заведующая кафедрой			/Малеева М. В./		04.02.2022 г
	(подпись)		(Фамилия И. О.)		(дата)
Руководитель ВКР			/Зубарева Е.С./		04.02.2022 г
	(подпись)		(Фамилия И. О.)		(дата)

АННОТАЦИЯ

Выпускная квалификационная работа выполнена на 81 странице, содержит 3 таблицы, 37 источников литературы, а также 2 приложения на 11 страницах.

Ключевые слова: функциональная грамотность, математическая грамотность, младший школьный возраст, обучение, PISA.

Библиографическое описание ВКР.

Колногорова, Ксения Дмитриевна. Формирование математической функциональной грамотности у младших школьников [Текст] : выпускная квалификационная работа / исполн.: К. Д. Колногорова; рук.: Зубарева Е. С.; М-во просвещения Рос. Федерации, Нижнетагил. гос. соц.-пед. ин-т (ф) ФГАОУ ВО «Рос. гос. проф.-пед. ун-т», Фак. психол.-пед. образования, Каф. психологии и педагогики дошкол. и нач. образования.  Нижний Тагил: НТГСПИ (ф) РГППУ, 2022.  81 л. Библиогр.: л. 65–69 (37 назв.).

Краткая характеристика содержания ВКР:

Тема: «Формирование математической функциональной грамотности у младших школьников».

Проблема исследования заключается недостаточность методической продукции, которая позволит формировать функциональную математическую грамотность.

Цель исследования: выявить и научно обосновать приемы, направленные на формирования математической функциональной грамотности у младших школьников на уроках математики.

На основе изучения и анализа психолого-педагогической и методической литературы изучили понятие «функциональная грамотность» и познакомились с её признаками, структурой и уровнями развития; определили особенности формирования математической функциональной грамотности в младшем школьном возрасте; проанализировали ресурсы и условия реализации комплекса заданий, направленных на развитие математической функциональной грамотности младших школьников; выявили наиболее эффективные приемы формирования математической функциональной грамотности у младших школьников в процессе обучения. Описали методику и результаты диагностики уровня сформированности математической функциональной грамотности; разработали педагогический проект, направленный на формирование математической функциональной грамотности у детей младшего школьного возраста.

Новизна выполненной выпускной квалификационной работы в сравнении с другими, родственными по тематике и целевому назначению заключается в том, что созданный педагогический проект представляет собой набор приёмов, последовательная реализация которых способствует успешному формированию математической функциональной грамотности у младших школьников.

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ		9
Глава 1.	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКОЙ ФУНКЦИОНАЛЬНОЙ ГРАМОСТНОСТИ У ДЕТЕЙ МЛАДШЕГО ШКОЛЬНОГО ВОЗРАСТА	13
1.1.	Сущность и содержание понятия «математическая функциональная грамотность», её признаки, структура и уровни развития	13
1.2.	Особенности формирования математической функциональной грамотности у младших школьников	20
1.3.	Характеристика приемов формирования математической функциональной грамотности младших школьников	30
ВЫВОДЫ	ПО ГЛАВЕ 1	43
Глава 2.	ПРОЕКТИРОВАНИЕ ДЕЯТЕЛЬНОСТИ ПЕДАГОГА ПО ФОРМИРОВАНИЮ МАТЕМАТИЧЕСКОЙ ФУНКЦИОНАЛЬНОЙ ГРАМОТНОСТИ У МЛАДШИХ ШКОЛЬНИКОВ	45
2.1.	Описание методик и результатов диагностики уровня сформированности математической функциональной грамотности у детей младшего школьного возраста	45
2.2.	Педагогический проект формирования математической функциональной грамотности у младших школьников	50
ВЫВОДЫ	ПО ГЛАВЕ 2	61
ЗАКЛЮЧЕНИЕ		62
СПИСОК ЛИТЕРАТУРЫ		65
ПРИЛОЖЕНИЕ 1. Комплексная диагностическая работа		70
ПРИЛОЖЕНИЕ 2. Комбинированная диагностическая работа для 2 класса по определению математической функциональной грамотности		78

ВВЕДЕНИЕ

В современном обществе существенно возрастает значимость качества математического образования.

Актуальность исследования формирования математической функциональной грамотности у младших школьников обусловлена значительными изменениями приоритетов школьного образования в России. Усиливается внимание к обеспечению адаптации обучающихся к существующим реалиям, наиболее значимыми становится использование математической функциональной грамотности как одно из необходимых условий эффективной жизнедеятельности для реализации их самообучения и саморазвития.

Единство образовательных требований к результатам освоения программ начального общего образования реализуется в Федеральном государственном образовательном стандарте на основе системно-деятельностного подхода, обеспечивающего системное и гармоничное развитие личности обучающегося, освоение им знаний, компетенций, необходимых как для жизни в современном обществе, так и для успешного обучения на уровне основного общего образования, а также в течение жизни [1].

Также, одним из показателей успешности вхождения в мировое образовательное пространство, является выполнение образовательных международных стандартов, в которых формирование математической функциональной грамотности обозначено в качестве одной из приоритетных задач. Формирование функциональной грамотности рассматривается как условие становления динамичной, творческой, ответственной и конкурентоспособной личности.

Математическая грамотность, по словам А. А. Леонтьева, предусматривает способность человека использовать приобретенные в течение жизни знания для решения широкого диапазона жизненных задач в различных сферах человеческой деятельности, общения и социальных отношений [13].

В условиях современной основной школы образовательный процесс ориентирован на формирование личностных, предметных и метапредметных результатов, достижение которых обеспечивает формирование личностных характеристик, соответствующих портрету выпускника основной школы. Одним из показателей их сформированности является уровень знаний и умений школьников, достаточный для нормального функционирования личности в системе социальных отношений. Одновременно с этим формируется и готовность учащихся максимально адаптироваться и функционировать во внешней среде.

По результатам тестирования Programme for International Student Assessment (Международная программа по оценке образовательных достижений учащихся) в 2018 году, Россия занимает в международном рейтинге качества образования 30 место по математической функциональной грамотности. Данные факты показывают необходимость ориентации части учебного процесса на формирование математической функциональной грамотности. В Федеральной целевой программе развития образования указывается на необходимость пристального внимания к системе оценочных процедур (включая международные исследования качества) в общем образовании [6].

Вопрос функциональной грамотности учащихся и всего подрастающего поколения также отражен в послании Президента: «Необходимо также уделять большое внимание функциональной грамотности наших детей, в целом всего подрастающего поколения. Это важно, чтобы наши дети были адаптированы к современной жизни» [2].

Психологии школьников, возрастным особенностям развития, в том числе детей младшего школьного возраста, посвящены фундаментальные труды ученых Л. С. Выготского, Д. Б. Эльконина. Вопросами изучения функциональной грамотности школьников занимались ученые И. В. Семенова, М. А. Ушакова, К. Т. Медеубаева, М. И. Козлова. Функциональной грамотности младшего школьного возраста посвятили свои труды Н. Ф. Виноградова и А. Е. Жумабаева. Работы Н. М. Евтыховой, Л. Л. Баговой, А. П. Карачевцевой посвящены математической функциональной грамотности у детей младшего школьного возраста.

На основе анализа нормативных документов, психолого-педагогической, методической литературы и педагогического опыта были определены следующие противоречия:

– между требованиями ФГОС НОО к результату образования, в том числе и к математической компетентности выпускников начальной школы и реальными недостаточно высокими результатами математической функциональной грамотности обучающихся;

– между достаточной теоретической изученностью проблемы формирования математической функциональной грамотности младших школьников и трудностями в отборе действенных педагогических средств по формированию математической функциональной грамотности обучающихся;

– между необходимостью развития математической грамотности у младших школьников и недостаточным количеством методических пособий, позволяющих целенаправленно и планомерно развивать математическую грамотность младших школьников.

Из данных противоречий нами была выделена следующая проблема: «Каковы педагогические условия формирования математической функциональной грамотности у детей младшего школьного возраста?».

Объект исследования – процесс формирования математической функциональной грамотности у младших школьников.

Предмет исследования – приёмы математической функциональной грамотности на уроках математики.

В соответствии с темой были определены цель и задачи исследования.

Цель: выявить и научно обосновать приемы, направленные на формирования математической функциональной грамотности у младших школьников на уроках математики.

Задачи:

1. На основе анализа психолого-педагогической и методической литературы изучить понятие «математическая функциональная грамотность» и ознакомиться с её признаками, структурой и уровнями развития;

2. Изучить психологические особенности детей младшего школьного возраста и определить особенности формирования математической функциональной грамотности в младшем школьном возрасте;

3. Выявить наиболее эффективные приемы формирования математической функциональной грамотности у младших школьников в процессе обучения;

4. Подобрать методики и описать результаты диагностики уровня сформированности математической функциональной грамотности;

5. Разработать педагогический проект, направленный на формирование математической функциональной грамотности у детей младшего школьного возраста.

Гипотеза исследования: процесс формирования математической функциональной грамотности будет эффективнее, если преподаватель в своей деятельности будет иметь, учитывать и использовать приёмы, направленные на формирование математической функциональной грамотности у младших школьников.

Методы теоретического исследования: анализ психолого-педагогической литературы, сравнение, обобщение.

Методы эмпирического исследования: тестирование, констатирующий эксперимент.

Практическая значимость заключается в том, что подобранные приемы при грамотном включении в урок, способствует успешному формированию функциональной грамотности у младших школьников.

Структура и объем: дипломная работа состоит из введения, двух глав, заключения, списка литературы (37 источников), двух приложений. Объем работы составляет 81 страницу.

ГЛАВА 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКОЙ ФУНКЦИОНАЛЬНОЙ ГРАМОСТНОСТИ ДЕТЕЙ МЛАДШЕГО ШКОЛЬНОГО ВОЗРАСТА

1. Сущность и содержание понятия «функциональная грамотность», её признаки, структура и уровни развития

Сложности современного мира требуют иного подхода в педагогике: это связано с появлением новых технологий, новых профессий, сфер экономики и с социально-психологическими изменениями самого человека. Окружающий мир больше не аналогово-текстологический, его сменяет визуально-цифровой – и это требует расширения и переосмысления понятия «функциональная грамотность» [34].

Само понятие было впервые употреблено на Всемирном конгрессе министров просвещения в Тегеране в 1965 году, и тогда под функциональной грамотностью подразумевалась как «совокупность умений читать и писать для использования в повседневной жизни и решения житейских проблем». Однако уже в 1978 Организация Объединенных наций по образованию, науке и культуре переработало и дополнило это понятие: «функционально грамотным считается только тот, кто может принимать участие во всех видах деятельности, в которых грамотность необходима для эффективного функционирования его группы и которые дают ему также возможность продолжать пользоваться чтением, письмом и счётом для своего собственного развития и для дальнейшего развития общины (социального окружения)» [5].

Буквально ещё через двенадцать лет Организация Объединенных наций по образованию, науке и культуре объявила Десятилетие грамотности в самой широкой интерпретации данного понятия с 2002 по 2012 гг., в декларации этого всемирного события функциональная грамотность становится больше, чем просто базовая грамотность: теперь это «…полноценно и эффективно функционировать как члены сообщества, родители, граждане и работники» [5].

Однако революция в науке и технике внесла свои коррективы в развитие и функциональной грамотности, и самого понятия о ней. Многие ученые приводят все новые и новые формулировки, стараясь наиболее полно описать функциональную грамотность современного человека.

Углубимся в понятие «функциональная грамотность». А. А. Леонтьев даёт следующее определение: «Функционально грамотный человек – это человек, который способен использовать все постоянно приобретаемые в течение жизни знания, умения и навыки для решения максимально широкого диапазона жизненных задач в различных сферах человеческой деятельности, общения и социальных отношений» [11].

Функциональная грамотность — «способность человека решать стандартные жизненные задачи в различных сферах жизни и деятельности на основе прикладных знаний».

Функционально грамотная личность — это человек, ориентирующийся в мире и действующий в соответствии с общественными ценностями, ожиданиями и интересами [27].

Основные признаки функционально грамотной личности: это человек самостоятельный, познающий и умеющий жить среди людей, обладающий определёнными качествами, ключевыми компетенциями.

Содержание функциональной грамотности:

— языковая грамотность;

— компьютерная и информационная грамотность;

— правовая грамотность;

— гражданская грамотность;

— финансовая грамотность;

— экологическая грамотность;

— профессиональные и специальные аспекты функциональной грамотности (менеджмент, PR, бизнес-планирование, новые технологии и т.д.).

Особое место в представлении о функциональной грамотности занимает деятельностная грамотность: способность ставить и изменять цели и задачи собственной деятельности, осуществлять коммуникацию, реализовывать простейшие акты деятельности в ситуации неопределенности [15].

Функциональная грамотность отражает общеучебную компетенцию, что на современном этапе обеспечивается за счет внедрения ФГОС на всех уровнях образования. Кроме того, функциональная грамотность упоминается в Концепции развития поликультурного образования в Российской Федерации. В нем подчеркивается, что только функциональная грамотность (владение современной техникой, языками и т.п.) позволяет современному человеку осваивать социальную и природную среду, активно работать в условиях интенсивной экономики и постиндустриальной цивилизации, стать гражданином мира в широком смысле [4].

Сам термин «грамотность» имеет специфическое содержание в данном исследовании. Здесь под грамотностью понимается скорее способность функционально использовать математические знания и умения, нежели мастерское владение этими знаниями в рамках требований школьной программы. И эту способность можно называть «функциональной математической грамотностью» [3].

Итак, математическая функциональная грамотность — способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и в будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину.

В принятом определении, «заниматься» математикой не означает выполнять простые физические или социальные математические действия (например, вычислить сдачу при покупке в магазине), под этим подразумевается более широкое использование математики в связи с самыми различными целями, например, высказать обоснованное мнение о бюджете, предлагаемом правительством [30].

Функциональная математическая грамотность включает также способность выделять в различных ситуациях математическую проблему и решать ее, а также наклонность выполнять такую деятельность, что достаточно часто связано с такими чертами характера, как уверенностью в себе и любознательностью.

Формирование функциональной грамотности на уроках математики невозможно без правильной и четкой математической речи. Для формирования грамотной, логически верной математической речи можно использовать составление математического словаря, написание математического диктанта, выполнение заданий, направленных на грамотное написание, произношение и употребление имен числительных, математических терминов [12].

На начальном этапе обучения главное — развивать умение каждого ребенка мыслить с помощью таких логических приемов, как анализ, синтез, сравнение, обобщение, классификация умозаключение, систематизация, отрицание, ограничение. Формированию функциональной грамотности на уроках в начальной школе помогут задания, соответствующие уровню логических приемов.

Результатом развития функциональной грамотности является овладение обучающимися системой ключевых компетенций, позволяющих молодым людям эффективно применять усвоенные знания в практической ситуации и успешно использовать в процессе социальной адаптации. Ключевые компетенции — это требование государства к качеству личности выпускника основной и средней школы в виде результатов образования, заявленные в федеральном государственном стандарте и учебных программах [19].

Как отмечалось выше, составляющими функциональной грамотности являются умения (ключевые компетенции или универсальные учебные действия) определённого типа, основанные на прочных знаниях, а именно: организационные, интеллектуальные, оценочные и коммуникативные.

Для успешного формирования и развития функциональной грамотности обучающихся, достижения ключевых и предметных компетенций необходимо соблюдать следующие условия:

— обучение должно носить деятельностный характер (формирование у школьников умений самостоятельной учебной деятельности, поэтому проблема функциональной грамотности рассматривается, как проблема деятельностная, как проблема поиска механизмов и способов быстрой адаптации в современном мире);

— программа должна быть взвешенной и учитывать индивидуальные интересы учащихся и их потребность в развитии (новый Стандарт соответствует данному условию);

— обучающиеся должны стать активными участниками процесса изучения нового материала;

— учебный процесс необходимо ориентировать на развитие самостоятельности и ответственности ученика за результаты своей деятельности;

— во внеурочной деятельности использовать продуктивные формы групповой работы [22].

Кроме того, для обеспечения продуктивности формирования функциональной грамотности школьников педагогам необходимо применять специальные активные, деятельностные, личностно-ориентированные, развивающие образовательные технологии, такие как:

— проблемно-диалогическая технология освоения новых знаний, позволяющая формировать организационные, интеллектуальные и другие умения, в том числе умение самостоятельно осуществлять деятельность изучения нового материала;

— технология проектной деятельности, обеспечивающая условия для формирования организационных, интеллектуальных, коммуникативных и оценочных умений (подготовка различных плакатов, памяток, моделей, организация и проведение выставок, викторин, конкурсов, спектаклей, мини-исследований, предусматривающих обязательную презентацию полученных результатов, и др.);

— уровневая дифференциация обучения, использование которой вносит определённые изменения в стиль взаимодействия учителя с учениками (ученик — это партнёр, имеющий право на принятие решений, например, о содержании своего образования, уровне его усвоения и т. д.), главная же задача и обязанность учителя — помочь ребёнку принять и выполнить принятое им решение;

— информационные и коммуникационные технологии, использование которых позволяет формировать основу таких важнейших интеллектуальных умений, как сравнение и обобщение, анализ и синтез;

— технология оценивания учебных достижений учащихся [17].

Математическая грамотность — это способность человека мыслить математически, формулировать, применять и интерпретировать математику для решения задач в разнообразных практических контекстах. Она включает в себя понятия, процедуры и факты, а также инструменты для описания, объяснения и предсказания явлений. Она помогает людям понять роль математики в мире, высказывать хорошо обоснованные суждения и принимать решения, которые должны принимать конструктивные, активные и размышляющие граждане в 21 веке.

В определении математической грамотности особое внимание уделяется использованию математики для решения практических задач в различных контекстах.

Для проведения проверки математической грамотности были выделены три направления: виды деятельности, содержание, ситуации [26].

Виды деятельности — задания, используемые в исследовании, группируются вокруг трех уровней компетентности. Первый — воспроизведение — включает проверку определений или простых вычислений, характерных для обычной проверки математической подготовки учащихся. Второй — установление связей — требует интеграции математических фактов и методов для решения явно сформулированных и до некоторой степени знакомых математических задач. Третий — размышления — включает проверку математического мышления, умения обобщать, глубоко понимать, использовать интуицию, анализировать предложенную ситуацию для выделения в ней проблемы, которая решается средствами математики, и формулирования этой проблемы [18].

Содержание проверки в данном исследовании группируется вокруг некоторых общих явлений или типов проблем, которые возникают при рассмотрении этих явлений. В качестве таких явлений предлагаются следующие: количество, пространство и форма, изменение и зависимости, неопределенность.

Один из важных аспектов математической грамотности — это применение математики в различных ситуациях, которые связаны с личной и школьной жизнью, местным обществом, общественной жизнью, работой и отдыхом [1].

В концепцию по математике было добавлено 8 навыков 21 века:

1. Критическое мышление;

2. Креативность;

3. Исследование и изучение;

4. Саморегуляция, инициативность, настойчивость;

5. Использование информации;

6. Системное мышление;

7. Коммуникация;

8. Рефлексия.

Основа организации исследования математической грамотности включает три структурных компонента:

1. Контекст, в котором представлена проблема;

2. Содержание математического образования, которое используется в заданиях;

3. Мыслительная деятельность, необходимая для того, чтобы связать контекст, в котором представлена проблема, с математическим содержанием, необходимым для её решения [25].

Таким образом, функциональная грамотность — это способность человека решать стандартные жизненные задачи в различных сферах жизни и деятельности на основе прикладных знаний. А под математической функциональной грамотностью понимается способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и в будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину. Функциональная математическая грамотность включает способность выделять в различных ситуациях математическую проблему и решать ее, а также наклонность выполнять такую деятельность, что достаточно часто связано с такими чертами характера, как уверенностью в себе и любознательностью. Для проведения проверки математической грамотности выделяют три основных направления: виды деятельности, содержание, ситуации.

1.2. Особенности формирования математической функциональной грамотности у младших школьников

Младший школьный возраст охватывает период жизни от 6 до 11 лет, когда он проходит обучение в начальных классах, и определяется важнейшим обстоятельством в жизни ребенка — его поступлением в школу. Для того чтобы определить особенности формирования математической функциональной грамотности, необходимо дать психолого-педагогическую характеристику данного возраста [16].

В это время происходит интенсивное биологическое развитие детского организма (центральной и вегетативной нервных систем, костной и мышечной систем, деятельности внутренних органов). В основе такой перестройки (ее еще называют вторым физиологическим кризом) лежит отчетливый эндокринный сдвиг — включаются в действие «новые» железы внутренней секреции и перестают действовать «старые». Такая физиологическая перестройка требует от организма ребенка большого напряжения для мобилизации всех резервов. В этот период возрастает подвижность нервных процессов, процессы возбуждения преобладают, и это определяет такие характерные особенности младших школьников, как повышенную эмоциональную возбудимость и непоседливость [28].

Поскольку мышечное развитие и способы управления им не идут синхронно, то у детей этого возраста есть особенности в организации движения. Развитие крупных мышц опережает развитие мелких, в связи с чем, дети лучше выполняют сильные и размашистые движения, чем мелкие и требующие точности (например, при письме). Вместе с тем растущая физическая выносливость, повышение работоспособности носят относительный характер, и в целом для детей остается характерной повышенная утомляемость и нервно-психическая ранимость. Их работоспособность обычно падает через 25 – 30 минут урока. Дети утомляются в случае посещения группы продленного дня, а также при повышенной эмоциональной насыщенности уроков и мероприятий [31].

Физиологические трансформации вызывают большие изменения в психической жизни ребенка. С вступлением в школьную жизнь у ребенка как бы открывается новая эпоха. Л. С. Выготский говорил, что расставание с дошкольным возрастом — это расставание с детской непосредственностью. Ребенок, попадая в школьное детство, оказывается в менее снисходительном и более суровом мире. И от того, как он к этим условиям приспособится, зависит очень многое. Преподавателям и родителям необходимо владеть знаниями о данном периоде развития ребенка, поскольку неблагоприятное его протекание для многих детей становится началом разочарований, причиной конфликтов в школе и дома, слабого овладения школьным материалом. А отрицательный эмоциональный заряд, полученный в начальных классах, может явиться конфликтом в будущем [29].

Младший школьный возраст, как и все возраста, открывается критическим, или переломным, периодом, который был описан в литературе раньше остальных, как кризис семи лет. Давно замечено, что ребенок при переходе от дошкольного к школьному возрасту очень резко меняется и становится более трудным в воспитательном отношении, чем прежде. Утеря непосредственности означает привнесение в наши поступки интеллектуального момента, который вклинивается между переживанием и непосредственным поступком, что является прямой противоположностью наивному и непосредственному действию, свойственному ребенку [13].

В 7-летнем возрасте мы имеем дело с началом возникновения такой структуры переживаний, когда ребенок начинает понимать, что значит «я радуюсь», «я огорчен», «я сердит», «я добрый», «я злой», т. е. у него возникает осмысленная ориентировка в собственных переживаниях. Благодаря этому выступают некоторые особенности, характеризующие кризис семи лет.

Таким образом, кризис 7 лет появляется на основе возникновения личного сознания. Основная симптоматика кризиса:

1. Потеря непосредственности. Между желанием и действием вклинивается переживание того, какое значение это действие будет иметь для самого ребенка;

2. Манерничанье: ребенок что-то из себя строит, что-то скрывает (уже душа закрыта);

3. Симптом «горькой конфеты»: ребенку плохо, но он старается этого не показать. Возникают трудности воспитания, ребенок начинает замыкаться и становится неуправляемым [23].

В основе этих симптомов и лежит обобщение переживаний. У ребенка возникла новая внутренняя жизнь, жизнь переживаний, которая прямо и непосредственно не накладывается на внешнюю жизнь. Но эта внутренняя жизнь небезразлична для внешней, она на нее влияет [10].

Возникновение внутренней жизни — чрезвычайно важный факт, теперь ориентация поведения будет осуществляться внутри этой внутренней жизни. Кризис требует перехода к новой социальной ситуации, требует нового содержания отношений. Ребенок должен вступить в отношения с обществом как с совокупностью людей, осуществляющих обязательную, общественно необходимую и общественно полезную деятельность. В наших условиях тенденция к ней выражается в стремлении скорее пойти в школу. Нередко более высокую ступень развития, которой ребенок достигает к семи годам, смешивают с проблемой готовности ребенка к школьному обучению. Наблюдения в первые дни пребывания ребенка в школе показывают, что готовности к обучению в школе у многих детей еще нет [17].

Из работ Л. С. Выготского известно, что каждая стадия психического развития ребенка характеризуется соответствующим типом ведущей деятельности. В период младшего школьного детства учебная деятельность является для ребенка ведущей. Следует отметить, что и на предыдущих стадиях своего развития ребенок учился, но лишь теперь учеба предстает перед ним как самостоятельная деятельность. В школьные годы учебная деятельность начинает занимать центральное место в деятельности ребенка. Все главные изменения в психическом развитии ребенка наблюдаемы на этой стадии, связаны в первую очередь с учебой [29].

С приходом в школу изменяется эмоциональная сфера ребенка. С одной стороны, у младших школьников, особенно первоклассников, в значительной степени сохраняется характерное и для дошкольников свойство бурно реагировать на отдельные, задевающие их, события и ситуации. Дети чувствительны к воздействиям окружающих условий жизни, впечатлительны и эмоционально отзывчивы. Они воспринимают прежде всего те объекты или свойства предметов, которые вызывают непосредственный эмоциональный отклик, эмоциональное отношение. Наглядное, яркое, живое воспринимается лучше всего. С другой стороны, поступление в школу порождает новые, специфические эмоциональные переживания, так как свобода дошкольного возраста сменяется зависимостью и подчинением новым правилам жизни. Ситуация школьной жизни вводит ребенка в строго нормированный мир отношений, требуя от него организованности, ответственности, дисциплинированности, хорошей успеваемости. Ужесточая условия жизни, новая социальная ситуация у каждого ребенка, поступившего в школу, повышает психическую напряженность. Это отражается и на здоровье младших школьников, и на их поведении. Под руководством учителя дети начинают усваивать содержание основных форм человеческой культуры (науки, искусства, морали) и учатся действовать в соответствии с традициями и новыми социальными ожиданиями людей. Именно в этом возрасте ребенок впервые отчетливо начинает осознавать отношения между ним и окружающими, разбираться в общественных мотивах поведения, нравственных оценках, значимости конфликтных ситуаций, то есть постепенно вступает в сознательную фазу формирования личности [22].

Принципиально меняется весь жизненный строй ребенка. Еще недавно в развитии маленького дошкольника игра являлась основным занятием, а теперь он школьник, изменилась вся система отношений с взрослыми и сверстниками. У ребенка появляется совершенно новая система отношений, а именно отношения с учителями, которые в глазах ребенка выступают «не заместителем родителей, а полномочным представителем общества, вооруженным всеми средствами контроля и оценки, действующим от имени и по поручению общества».

Знания для ребенка этого возраста не существуют без учителя. И если ребенок полюбил учителя, то стремление к знаниям у него, несомненно, повысится, урок станет для него интересным и желанным, а взаимодействие с учителем радостным и приносящим много полезных плодов. Если же ребенок недолюбливает учителя, то учение теряет для него всякую ценность [18].

Однако игра не исчезает в младшем школьном возрасте совсем, она приобретает иные формы и содержание. Игра занимает существенное место в жизни ребенка наряду с учебной деятельностью, прежде всего это игры с правилами, игры-драматизации. Многие ученики берут с собой на занятия свои любимые игрушки, а на переменах активно играют в них с друзьями, забывая о том, что они находятся в стенах школы. И, хотя, игра уже не занимает того важного места в жизни ребенка, которое было характерно для нее в дошкольном возрасте, она все еще имеет большое значение в психическом развитии младшего школьника.

Стоит отметить, что некоторые школьники в силу запаздывания своего общего психического развития попадают в это время в сложную ситуацию: для них еще не потеряла свою актуальность игровая деятельность, но в то же время школа предъявляет к ним новые требования, ставит перед необходимостью присвоения соответствующих младшему школьному возрасту форм жизнедеятельности, где ведущей уже выступает учебная, появляются новые социальные установки, новые социальные мотивы, связанные с чувством долга и ответственности, необходимости получения образования [15].

Огромное значение для формирования личности ребенка в возрасте 7 – 9 лет имеет коллектив, который формирует социальную направленность школьника. Особенно к концу младшего школьного возраста, ребенок стремиться к обществу других детей, интересуется делами класса, членом которого сам является. Особое значение для него начинает приобретать мнение сверстников. Школьники хотят занять свое место в классе, завоевать авторитет и уважение товарищей. Процесс включения ученика в школьный коллектив сложный, неоднозначный, нередко противоречивый. Прежде всего, данный процесс глубоко индивидуален. Школьники отличаются друг от друга состоянием здоровья, внешностью, чертами характера, степенью общительности, знаниями, умениями, поэтому они по-разному входят в систему коллективных отношений. Особенно трудно младшим школьникам, у которых еще недостаточно развиты самосознание и самооценка, умение правильно оценивать отношение к себе коллектива, товарищей, умение найти место в коллективе [32].

Стремление детей данного возраста состоит так же и в том, чтобы поскорее стать взрослыми, они во многом охотно подражают родителям, учителям, старшим братьям и сестрам. Желание этой взрослости дети реализуют во всех формах повседневной жизни: игры, общение со сверстниками, родителями, учителями, где ребенок активно может проявлять свою самостоятельность и независимость. Стремление поскорее стать взрослым это также непреодолимая тяга к получению знаний, таких как овладение письмом, чтением, желание начать говорить на иностранном языке. Таким образом, совершенно не обязательно напоминать ребенку, что он еще маленький и чрезмерно опекать его, а наоборот, пробовать поручать ему «важные» дела, возложить на него некоторую ответственность, причем, заведомо предполагая, что он успешно со всем справится. Таким образом, мы взрослые, делаем этот процесс взросления ощутимым для него.

Именно на этом этапе возможно наиболее эффективное воздействие на интеллектуальную и личностную сферы ребенка. Использование различных игр и развивающих упражнений в работе с младшими школьниками оказывает благотворное влияние на развитие не только познавательной, но и личностно-мотивационной сферы учащихся. Создаваемый на уроках благоприятный эмоциональный фон в огромной степени способствует развитию учебной мотивации, что является необходимым условием эффективной адаптации младшего школьника к условиям школьной среды и успешного протекания учебной деятельности, являющейся основной на данном периоде развития ребенка [24].

Возрастная особенность младших школьников — сравнительная слабость произвольного внимания. Значительно лучше развито у них непроизвольное внимание. Все новое, неожиданное, яркое, интересное само по себе привлекает внимание учеников безо всяких усилий с их стороны. Дети могут упустить существенные детали в учебном материале и обратить внимание на несущественные только потому, что они привлекают внимание. Кроме преобладания непроизвольного внимания к возрастной особенности относится также его сравнительно небольшая устойчивость. Первоклассники и отчасти второклассники еще не умеют длительно сосредоточиваться на работе, особенно если она неинтересна и однообразна; их внимание легко отвлекается. В результате дети могут не выполнить задание в срок, потерять темп и ритм деятельности, пропустить буквы в слове и слова в предложении. Только к третьему классу внимание может сохраняться непрерывно уже в течение всего урока [19].

Ведущие виды памяти у младших школьников — эмоциональная и образная. Дети быстрее и прочнее запоминают все яркое, интересное, все то, что вызывает эмоциональный отклик. В то же время, эмоциональная память не всегда сопровождается отношением к ожившему чувству, как к воспоминанию ранее пережитого. Так, ребенок, напуганный зубным врачом или директором школы, пугается при каждой встрече с ними, но не всегда осознает, с чем связано это чувство, поскольку произвольное воспроизведение чувств практически невозможно. Таким образом, несмотря на то что эмоциональная память обеспечивает быстрое и прочное запоминание информации, полагаться на точность ее сохранения можно не всегда. Тем более что если в обычных, спокойных условиях возрастание силы и яркости впечатления повышает четкость и прочность запоминания, то в экстремальных ситуациях (например, на контрольной) сильное потрясение ослабляет или даже полностью глушит то, что было воспроизведено [15].

Математическая грамотность включает в себя математические компетентности, которые можно формировать через специально разработанную систему задач:

1 группа – задачи, в которых требуется воспроизвести факты и методы, выполнить вычисления;

2 группа – задачи, в которых требуется установить связи и интегрировать материал из разных областей математики;

3 группа – задачи, в которых требуется выделить в жизненных ситуациях проблему, решаемую средствами математики, построить модель решения.

ФГОС утверждают, что предметные результаты освоения основной образовательной программы начального общего образования должны отражать:

— «использование начальных математических знаний для описания и объяснения окружающих предметов, процессов, явлений, а также оценки их количественных и пространственных отношений;

— приобретение начального опыта применения математических знаний для решения учебно-познавательных и учебно-практических задач» [1].

Учащиеся, овладевшие математической грамотностью, способны:

— распознавать проблемы, возникающие в окружающей действительности, которые могут быть решены средствами математики;

— формировать проблемы на языке математики;

— решать проблемы, используя математические знания и методы математического моделирования;

— интерпретировать полученные знания;

— формулировать и записывать окончательные решения [29].

В ходе уроков математики развивается математическая культура учащихся в целом. В понятие математическая культура входят: алгоритмическая культура, вычислительная культура, графическая культура, логическая культура, математическая грамотность. Дополнительные задания, применяемые в системе на различных этапах урока, позволяют развивать различные компоненты математической грамотности.

В различных источниках находили интересные задания, получился банк технологий, приемов, образцов заданий, которые я использую в рамках развития математической грамотности. Главное, чтобы эти задания были связаны с жизненной ситуацией [36].

Формирование математической грамотности обеспечивается за счёт применения современных образовательных технологий (проблемное, проектное обучение, игровые технологии, ИКТ, работы с символическим текстом, преобразование информации, работа с диаграммами, таблицами, чертежами), отбора и использования эффективных методов, приёмов и форм работы на уроках математики.

Таким образом, задачи по формированию математической грамотности обучающихся возможно реализовать при условии оптимального сочетания учебного содержания базового уровня образования и дополнительных курсов, направленных на совершенствование математических умений, использующихся в различных жизненных ситуациях [4].

Математическая грамотность младшего школьника как компонент функциональной грамотности трактуется как:

— понимание необходимости математических знаний для учения и повседневной жизни (для чего, где может пригодиться, где воспользуемся полученными знаниями);

— потребность и умение применять математику в повседневных (житейских) ситуациях: рассчитывать стоимость, массу, количество необходимого материала и т.д. находить, анализировать математическую информацию об объектах окружающей действительности, рассчитывать стоимость (протяженность, массу);

— способность различать математические объекты (числа, величины, фигуры), устанавливать математические отношения (длиннее-короче, быстрее-медленнее), зависимости (увеличивается, расходуется), сравнивать, классифицировать;

— совокупность умений: действовать по инструкции (алгоритму), решать учебные задачи, связанные с измерением, вычислениями, упорядочиванием, формулировать суждения с использованием математических терминов, знаков, свойств арифметических действий. Важно, чтобы ребята понимали, для чего эти знания. Важно понимать, когда вычисления выполнять письменно, а когда устно. Полезны сочетания устных и письменных вычислений, но все они должны быть применены в повседневной жизни [12].

Из сказанного следует, что на формирование функциональной математической грамотности у человека первостепенное значение оказывает период его обучения в младшей школе. Математическая грамотность младшего школьника, как компонент функциональной грамотности, трактуется, как способность различать математические объекты (числа, величины, фигуры), устанавливать математические отношения (длиннее-короче, быстрее-медленнее), зависимости (увеличивается, расходуется), сравнивать, классифицировать, решать задачи в 1-3 действия, связанные с бытовыми жизненными ситуациями (покупка, измерение, взвешивание). При этом следует обращать внимание на важность тщательной подготовки к планируемому уроку. В нем должны учитываться требования программы, а также необходимость детей быть активными в познавательном процессе. Ученику важно проявлять активность в мышлении, умении представлять, выражать свои мысли, делать предположения и аргументировать сказанное.

1.3. Характеристика методов и приемов формирования математической функциональной грамотности младших школьников

Современные требования времени таковы, что каждый день дети сталкиваются с огромным количеством задач, которые необходимо не только решить, но и найти рациональное и неординарное решение. Перед учителем ставятся новые задачи: научить не только грамотно решать эти задачи, но и делать выводы, систематизировать накопленные знания, уметь самостоятельно добывать необходимую информацию.

Исследования немецких ученых показали, что человек запоминает только 10% того, что он читает, 20% того, что слышит, 30% того, что видит; и только тогда, когда мы говорим и участвуем в реальной деятельности, он запоминает и усваивает материал на 90% [37].

Вот и встают перед учителем вопросы: как научить ребенка учиться, ориентироваться в большом объеме информации, работать с текстом? Как вызвать активную познавательную деятельность? Как вызвать положительное отношение к учебе? Как формировать функциональную грамотность? Появляется необходимость в новых педагогических технологиях, в эффективных формах образовательного процесса, в активных методах и приемах обучения, которые направлены на развитие познавательной, мыслительной активности, которая в свою очередь направлена на отработку, обогащение знаний каждого учащегося, развитие его функциональной грамотности [11].

Приём «Урок без темы». Описание: универсальный приём триз, направленный на создание внешней мотивации изучения темы урока. Данный прием позволяет привлечь интерес учащихся к изучению новой темы, не блокируя восприятия непонятными терминами.

Пример: Учитель записывает на доске слово «тема», выдерживает паузу до тех пор, пока все не обратят внимание на руку учителя, которая не хочет выводить саму тему [18].

Учитель: ребята, извините, но моя рука отказалась написать тему урока, и, кажется, неслучайно! Вот вам еще одна загадка, которую вы разгадаете уже в середине урока: почему рука отказалась записать тему урока?

Данный вопрос записывает в уголке классной доски.

Учитель: ребята, вам предстоит проанализировать и доказать, с точки зрения полезности, отсутствие темы в начале урока! Но начинать урок нам все равно надо, и начнем с хорошо знакомого материала…

Данный приём направлен на формирование функциональной грамотности младшего школьника. Он направлен на создание внешней мотивации для изучения любой математической темы и приближения её к жизни.

Приём «Ложная альтернатива» (прием триз). Описание: внимание слушателя уводится в сторону с помощью альтернативы «или - или», совершенно произвольно выраженной. Ни один из предлагаемых ответов не является верным [27].

Пример. Учитель предлагает вразброс обычные загадки и лжезагадки, дети должны их угадывать и указывать их тип. Например:

1. Сколько будет 8 + 4: 11 или 13?

2. Что растет не березе - яблоки или груши?

3. Слово "часы" - пишется как "чесы" или "чисы"?

4. Кто быстрее плавает - котенок или цыпленок?

5. Столица России - Париж или Минск?

6. Какие звери живут в Африке - мамонты или динозавры?

Данный приём направлен на развитие функциональной грамотности, в том числе и математической. Основывается на умении высказывать хорошо обоснованные математические суждения и использовать знания по предмету.

Приём «Шаг за шагом». Описание: приём интерактивного обучения. Используется для активизации полученных ранее знаний. Автор – Е. Д. Тимашева [15].

Ученики, шагая к доске, на каждый шаг называют термин, понятие, явление из изученного ранее материала. Тем самым актуализируя ранее полученные знания.

Приём «Я возьму тебя с собой»

Описание: Учитель загадывает признак, по которому будет собрано множество объектов. Задача класса угадать этот признак. Для этого они называют разнообразные предметы, а учитель говорит, возьмет ли он их с собой или нет. Игра продолжается, пока кто-то из учеников не догадается, какой признак объединяет все «взятые» предметы.

«Я беру тебя с собой» — гибкий прием, который можно изменять согласно теме урока.

Данный приём формирует способность человека осваивать и использовать математические знания для распознавания и постановки вопросов, для освоения новых знаний и объяснения явлений. Задача учителя — помочь ученику ориентироваться в обилии поступающей информации.

Приём «Хорошо — плохо» направлен на активизацию мыслительной деятельности обучающихся на уроке, формирование представления о том, как устроено противоречие. Формирует познавательные умений: обучающиеся осознанно и произвольно строят речевые высказывания в устной форме; устанавливают причинно-следственные связи; строят логические цепочки рассуждений и приводят доказательства.

Кроме этого формируются:

— умение находить положительные и отрицательные стороны в любом объекте, ситуации;

— умение разрешать противоречия;

— умение оценивать объект, ситуацию с разных позиций.

Приём «Фишбоун» (рыбий скелет/рыбья кость) — универсальный приём, которым можно пользоваться на уроках любого типа. Но наиболее эффективно «рыбья кость» применяется на занятиях обобщения и систематизации полученных знаний, чтобы помочь учащимся организовать полученную информацию в стройную систему. В основе Фишбоуна — схематическая диаграмма в форме рыбьего скелета. Для младшего школьного возраста подойдет более естественная форма рыбы – горизонтальная (рис. 1) [33].

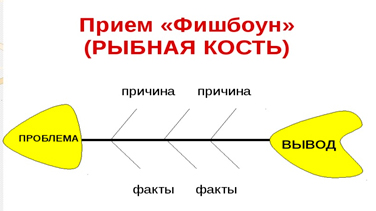
Рис. 1. Прием «Фишбоун» (рыбная кость)

Рассмотрим этот приём на теме урока окружающего мира «Какие бывают растения».

Проблема «Какие бывают растения?»

1 причина - деревья, факты - имеют один большой ствол, покрытый корой, от которого отходят ветки

2 причина - кустарники, факты - имеют много стволов- стволики

3 причина - травы, факты - имеют мягкий зелёный стебель

Вывод: чтобы определить вид растения, надо рассмотреть главный отличительный признак - вид ствола.

Этот приём позволяет учащимся проанализировать весь учебный материал, который был предложен в ходе изучения темы и сделать соответствующие выводы.

Приём «Займись синтезом». Описание: Интересный способ ввести себя в состояние творчества. Приём заключается в смешивании различных видов восприятия, способности ощущать вкус звуков, слышать цвета, обонять ощущения [26].

Пример. Чем пахнет слово «учитель»?

Каково на ощупь число 7?

Какой вкус у сиреневого цвета?

Какая форма у среды (как она выглядит)?

Какую музыку вы слышите, когда представляете лицо пожилого человека, смеющегося ребенка?

Развития творческого восприятия, совершенствования механизмов переключения можно добиться, регулярно работая над подобными упражнениями.

Функциональная грамотность учащихся на уроках математики формируется с помощью компетентностно-ориентированных заданий, интегрированных заданий и информационных технологий.

Компетентностные задания (задачи международного исследования РISA) способны привить интерес ученика к изучению математики, изменяют организацию традиционного урока. Они базируются на знаниях и умениях, и требуют умения применять накопленные знания в практической деятельности.

Интегрированные задания — это задания, объединяющие математику с другими предметами (математика — русский язык, экономика — математика, математика — литература, математика — познание мира) [35].

Кроме того, одним из главных средств развития функциональной грамотности в начальной школе являются информационные технологии (персональный сайт учителя, дистанционные олимпиады).

Важным аспектом в формировании функциональной грамотности младших школьников является формирование логической грамотности. В 1-х и 2-х классах, обучение проводится по следующей тематике:

«Смысл слов: «и», «или», «все», «некоторые», «каждый»

«Прием сравнения, выделение свойств предметов».

«Прием сравнения, существенные и несущественные свойства».

«Высказывания» (истинные, ложные).

«Прием классификации».

«Прием анализа и синтеза».

«Прием обобщения».

Примеры:

Разбей числа на группы, чтобы в каждой группе были числа, похожие между собой:

53, 33, 84, 75, 22, 13, 11, 44

По какому правилу записан каждый ряд чисел?

Продолжи его:

10, 30, 50, 70 …

14, 34, 54, 74 …

На каждом уроке математики отводится 5 - 10 минут на работу с заданиями, развивающими логическое и абстрактное мышление. Применение приема классификации на уроках математики способствует формированию положительных мотивов в учебной деятельности, так как подобная работа содержит элементы игры и элементы поисковой деятельности, что повышает активность учащихся и обеспечивает самостоятельное выполнение работы.

Такая система работы по развитию логического мышления учащихся направлена на формирование умственной деятельности детей. Дети учатся выявлять математические закономерности и отношения, выполнять посильное обобщение, делать выводы [10].

Основной целью математического образования должно быть развитие умения математически, логично и осознанно исследовать явления реального мира. Реализации этой цели может и должно способствовать решение на уроках математики разного рода нестандартных логических задач. Поэтому использование учителем школы этих задач на уроках математики является не только желаемым, но даже необходимым элементом обучения математике.

Нестандартные задачи требуют повышенного внимания к анализу условия и построения цепочки взаимосвязанных логических рассуждений. Примеры таких задач, ответ на которые необходимо логически обосновать:

В коробке лежат 5 карандашей: 2 синих и 3 красных. Сколько карандашей надо взять из коробки, не заглядывая в не, чтобы среди них был хотя бы 1 красный карандаш?

Использование таких задач расширяет математический кругозор младших школьников, способствует математическому развитию и повышает качество математической подготовленности.

Предлагая учащимся нестандартные задачи, мы формируем у них способность выполнять логические операции и одновременно развиваем их.

При решении занимательных задач преследуются следующие цели:

— формирование и развитие мыслительных операций: анализа и синтеза; сравнения, аналогии, обобщения и т.д.;

— развитие и тренинг мышления вообще и творческого в частности;

— поддержание интереса к предмету, к учебной деятельности (уникальность занимательной задачи служит мотивом к учебной деятельности);

— развитие качеств творческой личности, таких, как познавательная активность, усидчивость, упорство в достижении цели, самостоятельность;

— подготовка учащихся к творческой деятельности (творческое усвоение знаний, способов действий, умение переносить знания и способы действий в незнакомые ситуации и видеть новые функции объекта).

1 класс:

1. Расставить 6 книг на две полки так, чтобы на одной было на 2 книги больше, чем на другой.

2. В люстре 5 лампочек. Через некоторое время 3 лампочки перегорели. Сколько лампочек придется заменить?

2 класс:

1. В коробке умещается 10 красных и 6 синих бусинок. Какие бусинки мельче: красные или синие? (красные)

2. В парке 4 зеленых и коричневые скамейки. Зеленых скамеек больше. Сколько скамеек каждого цвета? (3 зеленые и 1 коричневая)

В современной педагогике игра, дидактическая игра используется в качестве самостоятельной технологии для освоения понятия темы и даже раздела учебного предмета, а также как элемент более общей технологии.

Игра является незаменимым помощником в работе, она формирует у учащихся такие качества, как интерес к учебному материалу, положительное отношение к школе, внимание, мышление. В ходе игры, учащиеся выполняя различные упражнения, приобретают новые знания, повторяют пройденный материал. Игра ставит учащихся в условия поиска, побуждает интерес к победе, значит, дети стремятся быть быстрыми, находчивыми, четко выполнять задания, соблюдая правила игры. В игре учащиеся учатся оказывать помощь товарищам, считаться с мнением и интересами других, сдерживать свои желания. В совместной деятельности детей возникают ситуации, требующие согласования действий, проявления доброжелательного отношения к сверстникам, умения отказаться от личных желаний ради достижения общей цели. Включение в урок игр и игровых моментов делает процесс обучения интересным, создаёт у детей бодрое рабочее настроение, облегчает усвоение учебного материала. В зависимости от цели, темы и характера игры игровой момент включаю на различных этапах урока. Ниже представлен ряд работ, используемых на уроках математики способствующий развитию функциональной математической грамотности младших школьников [27].

1.  Работа над задачей.

Многие ученики только после повторного анализа осознают план решения задачи. Это путь к выработке твердых знаний по математике.

2. Решение задач разными способами.

Мало уделяется внимания решению задач разными способами в основном из-за недостатка времени. Но это умение свидетельствует о достаточно высоком математическом развитии.

3. Представление ситуации, описанной в задачи и её моделирование:

а) с помощью отрезков:

Лягушка встречала гостей. Лиса пришла раньше Медведя, Волк позже Зайца, Медведь раньше Зайца, Сорока позже Волка.

Кто пришёл раньше всех?  Кто пришёл позже всех? В каком порядке приходили гости? (обозначь на отрезке)

б) с помощью рисунка:

На грядке сидели 6 мышек. К ним подбежали ещё 3. Кот подкрался и схватил одну. Сколько мышек осталось на грядке?

в) с помощью чертежа.

Обращаем внимание детей на детали, которые нужно обязательно представить, и которые можно опустить.

4. Разбивка текста задачи на значимые части.

5. Решение задач с недостающими или лишними данными.

Работа над задачей с недостающими и лишними данными воспитывает у детей привычку лучше осмысливать связи между искомым и данными.

Задача: в первом букете ромашки. Это на 12 ромашек больше, чем во втором букете. Сколько ромашек в двух букетах?

6. Самостоятельное составление задач учениками:

1) используя слова: больше на несколько, меньше на несколько единиц, в несколько раз больше, в несколько раз меньше;

2) по данному плану ее решения,

3) действиям и ответу;

4) по выражению [16].

7. Объяснение готового решения задачи.

8. Изменение вопроса задачи.

У Иры 5 роз, а у Оли на 2 розы меньше. Сколько роз у Оли?

Измени вопрос так, чтобы задача решалась в 2 действия.

9. Составление разных выражений к данным задачам

10. Выбор выражений, которые являются решением задачи.

11. Выбор способа записи решения задачи (выражением, уравнением, по действиям, с пояснением, с вопросами).

12. Использование приема сравнения задач и их решений.

13. Выбор решения из двух предложенных (верного и неверного).

14. Изменение условия задачи так, чтобы задача решалась другим действием.

15. Закончить решение задачи.

16. Составление аналогичной задачи с измененными данными.

17. Составление и решение обратных задач [23].

Развитие логического мышления младших школьников основывается на решении нестандартных задач на уроках математики и внеклассных занятиях. Нестандартные задачи требуют повышенного внимания к анализу условия и построения цепочки взаимосвязанных логических рассуждений. Приведем примеры таких задач, ответ на которые необходимо логически обосновать:

1. Логические задачи.

В клетке находились 3 попугая. Трое ребят купили по одному из этих попугаев, и один попугай остался в клетке. Как это могло случиться?

2. Задачи, связанные с величинами.

Слонёнок заболел. Для его лечения требуется ровно 2 л сока, а у доктора Айболита есть только полная пятилитровая банка с соком и пустая трёхлитровая банка. Как Айболиту отмерить ровно 2 л сока?

3. Расстановки. Задачи на промежутки.

Как расставить 5 кубиков в 2 ряда так, чтобы в каждом ряду было по 3 кубика? Нарисуй.

4. Задачи-шутки.

На дереве сидели 10 птиц. Охотник выстрелил и подстрелил одну птицу. Сколько птиц осталось на дереве?

5. Арифметические задачи, требующие особых приёмов решения.

У Оли и Коли 8 орехов. Сколько орехов у каждого, если у Коли на 2 ореха больше?

6. Задачи на планирование действий [19].

Хотят поскорее поджарить 3 ломтика хлеба. На сковороде умещается лишь 2 ломтика, причем на поджаривание одной стороны ломтика затрачивается 1 мин. Как поджарить с обеих сторон все 3 ломтика хлеба за 3 мин?

Как показывает практика, одним из эффективных способов развития функциональной грамотности является компетентностно-ориентированное задание. Кроме того, решение задач практического содержания направлено на привитие интереса к изучению математики. Такие задания базируются на знаниях и умениях и требуют умения применять накопленные знания в практической деятельности. Занятия направлены на развитие у учащихся логического, алгоритмического, пространственного мышления, внимания. Задания носят творческий характер. Они позволяют рассматривать объект с разных точек зрения, учат анализу, синтезу, оценочным суждениям, воспитывают внимание, способствуют развитию познавательного интереса и активности учащихся.  Занимательный материал, в виде математических ребусов, головоломок, волшебных и магических квадратов, математических загадок, стихов, игр, помогает активизировать мыслительные процессы, развивает познавательную активность, наблюдательность, внимание, память, поддерживает интерес к изучаемому. Создание на занятиях ситуаций активного поиска, предоставление возможности сделать собственное «открытие», знакомство с оригинальными путями рассуждений, овладение элементарными навыками исследовательской деятельности позволят обучающимся реализовать свои возможности, развить способности самостоятельной познавательной деятельности, приобрести уверенность в своих силах.

Таким образом, задачи по формированию функциональной грамотности, в частности, математической грамотности обучающихся, возможно реализовать при условии оптимального сочетания учебного содержания базового уровня образования и дополнительных курсов, направленных на совершенствование прикладных математических умений, использующихся в различных жизненных ситуациях [30].

Для развития логического мышления можно использовать различные задания: логические цепочки, магические квадраты, задачи в стихах, головоломки, математические загадки, кроссворды, геометрические задания со счётными палочками, логические задачи со временем, весом, комбинаторные задачи. Формирование логического мышления – это важная составная часть педагогического процесса. Помочь в полной мере проявить свои способности, развить инициативу, самостоятельность, творческий потенциал - одна из основных задач современной школы [41].

Все учителя начальных классов на своих уроках используют коллективные виды работ. Они делают урок более интересным, живым, воспитывают у детей сознательное отношение к учебному труду, активизируют мыслительную деятельность, дают возможность многократно повторять материал, помогают учителю объяснять и постоянно контролировать знания, умения и навыки у ребят всего класса. У детей повышается уровень развития, обучения и воспитания. А учитель получает возможность реально осуществить индивидуальный подход к обучающимся.

При организации работы в парах и группах каждый ученик мыслит, не просто сидит на уроке, предлагает своё мнение, пусть оно и неверное, в группах рождаются споры, обсуждаются разные варианты решения, идёт взаимообучение детей в процессе учебной дискуссии, учебного диалога.

Таким образом, перечисленные приёмы формирования математической функциональной грамотности младших школьников способствуют развитию информационно-образовательной среды, направленной на повышение математической функциональной грамотности учащихся, обеспечивающей личное саморазвитие, самостоятельность в приобретении знаний, формирующей коммуникативные навыки, умения использовать информацию и технологии, решать проблемы, предприимчивость и креативность. Учитель должен увлечь и «заразить» детей, показать им значимость их деятельности и вселить уверенность в своих силах. При условии успешности решения поставленных задач мы выполним главную цель формирования функционально-грамотной личности. Получим формирование в общеобразовательных школах интеллектуального, физически и духовно развитого гражданина. Все эти приемы помогают значительно улучшить восприятие предмета школьником, вызывают интерес к поставленным задачам. Данные приёмы лучше вводить постепенно, воспитывая у учащихся культуру дискуссии и сотрудничества. Применять данные приёмы не обязательно все на одном уроке, главное, чтобы работа велась в системе.

ВЫВОДЫ ПО ГЛАВЕ 1

В ходе изучения научной литературы по теме исследования, познакомились с понятием «математическая функциональная грамотность». Определили, что под данным феноменом мы будем понимать способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и в будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину.

Дальнейший анализ психолого-педагогической литературы позволил выявить признаки, а также уровни формирования математической функциональной грамотности.

Изучили особенности формирования математической функциональной грамотности у детей младшего школьного возраста. Определили, что на формирование функциональной математической грамотности у человека первостепенное значение оказывает период его обучения в младшей школе. Математическая грамотность младшего школьника как компонент функциональной грамотности трактуется как способность различать математические объекты, устанавливать математические отношения, зависимости, сравнивать, классифицировать, решать задачи в 1-3 действия, связанные с бытовыми жизненными ситуациями.

В уроках, направленных на формирование математической функциональной грамотности должны учитываться требования программы, а также необходимость детей быть активными в познавательном процессе.

Перечисленные нами методы и приемы формирования математической функциональной грамотности младших школьников способствуют развитию информационно-образовательной среды, направленной на повышение функциональной грамотности учащихся, обеспечивающей личное саморазвитие, самостоятельность в приобретении знаний, формирующей коммуникативные навыки, умения использовать информацию и технологии, решать проблемы, предприимчивость и креативность. Учитель должен увлечь и «заразить» детей, показать им значимость их деятельности и вселить уверенность в своих силах. При условии успешности решения поставленных задач мы выполним главную цель формирования функционально-грамотной личности т.е. формирование в общеобразовательных школах интеллектуального, физически и духовно развитого гражданина.

Цель учителя научить учащихся добывать знания, умения, навыки и применять их в практических ситуациях, оценивая факты, явления, события и на основе полученных знаний принимать решения, действовать. Все методы, используемые педагогом, должны быть направлены на развитие познавательной, мыслительной активности, которая в свою очередь направлена на отработку, обогащение знаний каждого учащегося, развитие его функциональной грамотности.

ГЛАВА 2. ПРОЕКТИРОВАНИЕ ДЕЯТЕЛЬНОСТИ ПЕДАГОГА ПО ФОРМИРОВАНИЮ МАТЕМАТИЧЕСКОЙ ФУНКЦИОНАЛЬНОЙ ГРАМОТНОСТИ У МЛАДШИХ ШКОЛЬНИКОВ

2.1. Методы и результаты исследования уровня сформированности математической функциональной грамотности у детей младшего школьного возраста

С целью выявления уровня сформированности математической функциональной грамотности нами были выбраны комбинированные диагностические работы для 2 класса разработанные Жидких Н. В. и Кокиной М. А. (Приложение 1) и работа, разработанная Локтиновой Натальей Васильевной (Приложение 2).

Исследование уровня математической функциональной грамотности младших школьников было проведено на базе Муниципального бюджетного общеобразовательного учреждения средняя общеобразовательная школа № 90 (г. Нижний Тагил).

Характеристика выборки: в исследовании приняли участие дети младшего школьного возраста, ученики 2 «А» класса. Общее количество опрошенных составило 22 человека в возрасте 8–9 лет, из них мальчиков – 11, девочек – 11.

Этапы исследования.

Исследование было организовано поэтапно. На первом этапе – подготовительном – изучалась и анализировалась психолого-педагогическая литература по теме исследования. Определялись теоретические основы исследования, уточнялись гипотеза, задачи и пути их решения. Вырабатывался план проведения эмпирического исследования, происходил подбор психодиагностического инструментария, подготавливались бланки и тексты диагностических работ.

На втором диагностическом этапе организовывалось и проводились диагностики с целью выявления уровня математической функциональной грамотности у детей младшего школьного возраста Муниципального бюджетного общеобразовательного учреждения средней общеобразовательной школы № 90.

На третьем этапе обрабатывались полученные данные.

Комбинированная диагностическая работа для 2 класса по определению математической функциональной грамотности, разработанная Натальей Викторовной Жидких и Кокиной Мариной Александровной, состоит из четырех заданий, каждое из которых описывает одну ситуацию. В каждом из заданий представлено по два вопроса. Таким образом, всего в работе 8 вопросов, на которые ученикам второго класса необходимо было дать ответ. На выполнение работы было отведено 40 минут.

Диагностическая работа включает задания с разной формой ответа. При ответе на вопрос с выбором ответа, нужно отметить ответ, который считаете верным, поставив знак «√». При ответе на вопрос с кратким ответом, младшие школьники записывали ответ в специально отведенном месте после слов «Ответ», «числовое выражение».

В работе также есть вопросы, к которым нужно не только дать ответ, но и записать решение или объяснение. В этих заданиях написано: «запишите решение», «докажите», «объясните».

После проведения комбинированной диагностической работы Жидких Н. В. и Кокиной М. А. (рис.2):

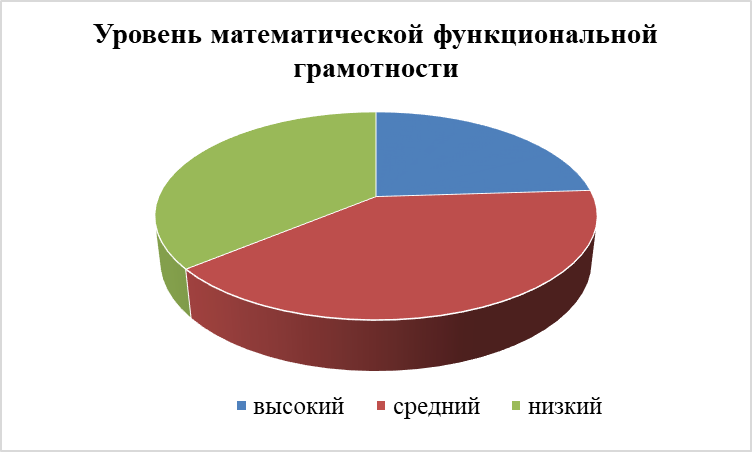
Рис.2 Уровень математической функциональной грамотности

— высокий уровень познавательной активности у 5 учащихся;

— средний уровень познавательной активности продемонстрировали 11 учащихся;

— низкий уровень познавательной активности зафиксирован у 7 обучающихся.

Анализируя данные диаграммы, можно отметить, что у большинства младших школьников был выявлен средний уровень математической функциональной грамотности (40%).

Далее проведена диагностическая работа с целью определения уровня усвоения учащимися математической и финансовой грамотности за второй класс общеобразовательной школы и выявление элементов содержания, вызывающих наибольшие затруднения. Разработчик: Локтионова Наталья Васильевна.

Для выполнения заданий нужна ручка, линейка, простой карандаш. Дополнительное оборудование и материалы не требуются. Ответы, учащиеся записывают в контрольно-измерительных материалах.

Время выполнения комбинированной диагностической работы —45 минут.

Работа составлена в одном варианте. Комбинированная диагностическая работа включает в себя 10 заданий (табл. 1).

Таблица 1

Содержание диагностической работы

№п.п.	Раздел содержания	Количество заданий
1	Математическая грамотность	7
2	Финансовая грамотность	3
	ИТОГО:	10

Задание считается выполненным верно, если ученик дал ответ, полностью совпадающий с эталоном. Задание № 10 оценивается 1 баллом. Задания № 1-9 оцениваются в соответствии с критериями. За выполнение заданий, оцениваемых одним баллом, выставляется 1 балл за полный верный ответ и 0 баллов за неверный ответ. За выполнение заданий, оцениваемых в 2-5 балла, в зависимости от полноты и правильности ответа выставляется от 0 до 5 баллов. Эти задания считаются выполненными, если учащийся получает за них хотя бы один балл.

Максимальный суммарный балл за всю работу — 35 (табл. 2).

Таблица 2

План комбинированной диагностической работы

1	2	3
№ задания	Контролируемы умения	Максимальный балл
1	Развитие математической речи. Соотнесение знаковой и словесной формулировки.	5 баллов
2	Знание математических терминов.	4 балла
3	Знание величин и применение их в жизненных ситуациях.	5 баллов
4	Умение работать над текстовой задачей (связь условия задачи и вопроса задачи). Разбор и выбор решения задачи в зависимости от поставленного вопроса.	2 балла
5	Умение работать над текстовой задачей (связь условия задачи и вопроса задачи). Разбор и выбор решения задачи в зависимости от поставленного вопроса.	2 балла
6	Умение работать над текстовой задачей. Овладение логическими действиями и операциями: сравнение, сопоставление, анализ представленной информации.	4 балла
7	Овладение логическими действиями и операциями: сравнение, сопоставление, анализ, обобщение представленной информации.	5 баллов
8	Понимать, что такое «семейный бюджет». Уметь делать несложные расчеты семейного бюджета. Знать, что такое доходы и расходы семьи.	2 балла
9	Работа с информацией. Чтение графика. Знать, что такое доходы и расходы семьи. Понимать, что такое «семейный бюджет».	5 баллов
1	2	3
10	Числа и величины. Сравнение и упорядочение чисел, знаки сравнения. Понимать, как пользоваться безналичными деньгами.	1 балл

Уровни математической функциональной грамотности:

Недостаточный — выполнено менее 30% заданий работы (задание считается выполненным, если получен хотя бы 1 балл);

Пониженный — 30 - 49% выполнения всей работы;

Базовый — 50% - 75% выполнения всей работы и набрано менее 75% от максимального балла;

Повышенный — выполнено более 75% заданий и набрано не менее 75% от максимального балла за выполнение всей работы.

После проведения диагностической работы Локтионовой Натальи Васильевны, получили следующие результаты (рис. 3):

Рис. 3 Уровень математической функциональной грамотности

— недостаточный уровень у 12 %, что говорит о не сформированности функциональных умений и недостаточности математических знаний;

— пониженный уровень у 26 % обучающихся, математическая функциональная грамотность на низком уровне, что свидетельствует о пороге, при достижении которого учащиеся начинают демонстрировать применение знаний и умений в простейших не учебных ситуациях;

— базовый уровень у большинства обучающихся — 38%, что свидетельствует о среднем уровне формирования математической функциональной грамотности — обучающиеся проявляют способность использовать имеющиеся знания и умения для получения новой информации;

— повышенный уровень продемонстрировали лишь 24 %, овладение и математическими знаниями, и умением их применять в жизни. Это ученики самостоятельно мыслящие и способные функционировать в сложных условиях.

По итогам проведенных методик можно констатировать, что в данном классе в основном средний уровень математической функциональной грамотности. Это говорит о хорошей сформированности математических знаний по предмету и недостатке применения этих знаний в реальной жизни на практике.

2.2. Педагогический проект формирования математической функциональной грамотности у младших школьников

В условиях социально-экономической модернизации обществу необходим человек, функционально грамотный, умеющий работать на результат, способный к определенным, социально значимым достижениям. Все данные качества начинают формироваться в начальной школе.

Функциональная грамотность – это уровень образованности, который может быть достигнут учащимися за время обучения в школе, и предполагает способность человека решать стандартные жизненные задачи в различных сферах жизни.

Изучив уровень математической функциональной грамотности обучающихся 2 класса, пришли к выводу, что в урок необходимо включить приёмы, направленные на формирование математической функциональной грамотности.

Цель: формирование математической функциональной грамотности у младших школьников на уроках математики.

Задачи:

1. Изучить понятие «математическая функциональная грамотность» и ознакомиться с её признаками, структурой и уровнями развития;

2. Изучить психологические особенности детей младшего школьного возраста и определить особенности формирования математической функциональной грамотности в младшем школьном возрасте;

3. Выявить наиболее эффективные приемы формирования математической функциональной грамотности у младших школьников в процессе обучения;

4. Подобрать методики и описать результаты диагностики уровня сформированности математической функциональной грамотности;

5. Разработать педагогический проект, направленный на формирование математической функциональной грамотности у детей младшего школьного возраста.

Сроки реализации проекта: 1 декабря 2021 года – 1 февраля 2022 года.

Педагогическое проектирование направлено на подбор и систематизацию приемов, применение которых при организации учебной деятельности школьников позволит развивать умения, направленные на развитие математической функциональной грамотности у младших школьников.

Разнообразие приёмов, их дифференциация, позволят детям выбрать задания того уровня, с которым они лучше справятся, и будет возможность попробовать выполнить задание другого уровня.

На этапе анализа объекта проектирования необходимо, прежде всего, определить, что мы будем проектировать: ситуацию, систему или процесс. В качестве объекта проектирования выбран процесс развития математической функциональной грамотности у младших школьников. В нашей работе объект проектирования разработан на уровне проектирования (создание проекта), так как модель можно использовать на практике. При проектировании целесообразной является следующая форма проектирования – набор приёмов, направленных на развитие математической грамотности у младших школьников.

Приём — кратковременное взаимодействие между преподавателем и учениками, направленное на передачу и усвоение конкретного знания, умения, навыка. С целью выработки у учащихся умений и навыков им даются задания на выполнение упражнений и на решение задач. Эти задания расположены в такой последовательности, чтобы обеспечить индивидуальную работу в зависимости от уровня подготовленности учащихся.

На подготовительном этапе был проведён первичный замер уровня развития математической функциональной грамотности, данные наблюдения помогли выяснить средний уровень готовности учащихся в решении заданий. Свидетельством данных результатов являются такие проблемы как:

– не умение обосновать свой ответ и привести аргументы;

– затруднение в нахождении решения на тот или иной вопрос.

Анализ результатов позволил выявить проблемное поле на устранение которого были направлены задания исследовательского характера, как средство развития математической грамотности.

Проблемное поле и пути его решения:

1) установление связей и интеграцию материала из разных математических тем, необходимого для решения поставленной проблемы;

2) недостаточный уровень развития навыков, направленных на применение математических знаний на практике, в жизни;

3) низкий уровень развития математической грамотности у младших школьников.

Пути решения:

1) проанализировав программу по математике, включили в уроки из изученных младшими школьниками тем, приёмы для повышения уровня развития математической функциональной грамотности;

2) подобрали интересные, разнообразные, доступные для восприятия задачи;

Проектирование предполагало моделирование, проектирование и конструирование; подбор приёмов к урокам по конкретной тематике.

Первый этап — педагогическое моделирование, предполагающее разработку целей и основной идеи создаваемого комплекса. На этапе проектирования мы определили его составные части и внутреннюю структуру каждой части. В рамках этих этапов осуществлён анализ литературы по проблеме исследования. На этапе конструирования осуществлялся процесс подбора и наполнения конкретных приёмов, направленных на формирование математической функциональной грамотности.

Просмотрев и проанализировав ряд приёмов, мы определили их целевые ориентиры, направленность и возможность реализации в том или ином фрагменте урока математики во 2 классе.

Второй этап - педагогическое проектирование (создание проекта), включающее в себя дальнейшую разработку созданной модели и доведение её до уровня практического использования. Подобраны задания, применение которых обеспечит развитие математической грамотности у обучающихся 2 класса. Все задание имеют практический характер и предполагается самостоятельное, или совместное с учителем, сверстниками выполнение практических проб. Подобранные и классифицированные по уровням задания можно использовать на уроках, при организации индивидуальной работы.

Связь приема и урока позволит систематизировать материал по определенной проблеме, поэтому он построен с учетом принципов: системности — предполагает, чтобы изложение учебного материала доводилось до уровня системности в создании учащихся, чтобы задания давались учащимся не только в определённой последовательности, но, чтобы они были взаимосвязанными.

Приёмы, направленные на формирование математической функциональной грамотности, будут реализованы во 2 «А» классе Муниципального бюджетного общеобразовательного учреждения средней общеобразовательной школе №90, в котором обучается 22 человека, из них 14 мальчиков и 13 девочек. Большинство из них 2013 года рождения. Многие дети посещали детский сад, умеют общаться со сверстниками и взрослыми, знают основные правила общения, способны управлять своим поведением. В классе нет инертных и замкнутых детей, трудно контактирующих с коллективом. В целом класс активный. Дети доброжелательны, способны дружить, сопереживать друг другу.

Класс обучается по программе «Школа России». Главная идея программы: «Школа России» создается в России и для России. Школа России должна стать школой духовно-нравственного развития. Именно такая школа будет достойна России.

«Школа России» - это учебно-методический комплект для 4-летней начальной школы. Научный руководитель комплекта - Андрей Анатольевич Плешаков, кандидат педагогических наук. В качестве единого целостного комплект «Школа России» работает с 2001 года. «Школа России» - это один из самых известных и востребованных учебно-методических комплектов для обучения в начальной школе. УМК постоянно обновляется и является надёжным инструментом реализации стандарта второго поколения. Ведущей целевой установкой УМК «Школа России» на протяжении всех лет было и является: «Воспитание гуманного, творческого, социально активного человека - гражданина и патриота России, уважительно и бережно относящегося к среде своего обитания, к своей семье, к природному и культурному достоянию своей малой Родины, своей многонациональной страны и всего человечества»

Для данной образовательной системы характерны следующие принципы:

1. системность — все учебники и учебные пособия основаны на единых подходах к содержанию, сохраняют методологическое, дидактическое, психологическое и методическое единство, в них используются одни и те же основные образовательные технологии, которые, не меняясь по сути, трансформируются на каждом этапе обучения;

2. непрерывность — «Школа России» — это совокупность предметных курсов от 1 до 4 классов;

3. преемственность — непрерываемость на границах различных этапов или форм обучения.

Все перечисленные принципы помогают добиться желаемого результата и привить у детей интерес к обучению, а самое главное вовлечь всех обучающихся в учебную деятельность, создать эмоциональный настрой и доброжелательное отношение к каждому обучающемуся.

Основной особенностью методов и форм является то, что предпочтение отдается проблемно-поисковой и творческой деятельности младших школьников. Такой подход предусматривает создание проблемных ситуаций, выдвижение предположений, поиск доказательств, формулирование выводов, сопоставление результатов с эталоном.

В ходе подготовки проекта велась непрерывная работа с опорой на учебно-методический комплекс для включения приёмов формирования математической функциональной грамотности в уроки математики. Задания подбирались из учебников по математике, методических пособий для 2 класса учебно-методического комплекта «Школа России» (табл. 3).

Таблица 3

Тематический план проекта

1	2	3	4
№ п/п	Тема урока	Задача формирования математической грамотности	Приемы организации деятельности
1.	Числа от 1 до 20. Образование, чтение и запись чисел от 1 до 20.	Развивать логическое мышление; способствовать формированию математических знаний и умений	Приём «Ложная альтернатива»; логическая задача.
2.	Метр. Таблица единиц длины.	Развивать понимание необходимости математических знаний для учения и повседневной жизни; способствовать формированию математических знаний и умений.	Приём синтеза; задачи, связанные с величинами.
3.	Десяток. Устная нумерация чисел в пределах 100.	Развивать способность различать математические объекты, устанавливать математические отношения.	Приём «Урок без темы»; «дополни задачу».

Тема урока: Числа от 1 до 20. Образование, чтение и запись чисел от 1 до 20.

Задачи урока, направленные на формирование математической функциональной грамотности: развивать логическое мышление; способствовать формированию математических знаний и умений.

На данном уроке целесообразно использование приема «Ложная альтернатива». Включение приема в урок: учитель предлагает в разброс обычные загадки и лжезагадки, дети должны их угадывать и указывать их тип. Примеры вопросов:

1. Сколько будет 8 + 4: 11 или 13?

2. После вторника наступает понедельник или пятница?

2. Что растет не березе - яблоки или груши?

3. Слово "часы" - пишется как "чесы" или "чисы"?

4. Кто быстрее плавает - котенок или цыпленок?

5. Столица России - Париж или Минск?

6. Какие звери живут в Африке - мамонты или динозавры?

Так же в рамках данного урока необходимо обратиться к задаче, направленной на развитие логического мышления. Варианты задач:

1. В магазине было 3 холодильника. Продали меньше, чем осталось. Сколько холодильников продали?

2. Брат и сестра пришли в школу одновременно. Брат шёл быстрее. Кто из них вышел раньше?

3. Аркадий – сын Романа, Роман – сын Василия. Кем приходится Аркадий Василию, а Василий Аркадию?

4. Росли три вербы, на каждой вербе – по 2 ветки. На каждой ветке – по 2 груши. Сколько всего груш?

5. Летела стая уток. Охотник выстрелил и одну убил. Сколько уток осталось?

6. На верёвку завязали 5 узлов. На сколько частей эти узлы разделили верёвку?

7. Рыбак поймал окуня, ерша и щуку. Щуку он поймал раньше, чем окуня, а ерша позже, чем щуку. Какая рыба поймана раньше всех? Можно ли сказать, какая рыба поймана позже всех?

8. Что тяжелее 1 кг ваты или 1 кг железа.

9. В банке столько же воды, сколько в кастрюле, а в кастрюле столько же воды, сколько в миске. Где больше воды: в банке или миске?

10. Оля выше Кати. Кто из девочек ниже?

11. По направлению к городу ехало 3 машины, а навстречу им ехало 5 автобусов. Сколько машин ехало в город?

12. Марина и Оля сёстры. Марина сказала, что у неё 2 брата, а Оля сказала, что у неё тоже два брата. Сколько детей в семье?

13. Масса петуха, стоящего на двух ногах 4кг. Какова будет масса петуха, если он встанет на одну ногу?

При использовании в этом уроке данных приемов, мы решим поставленные задачи.

Тема урока: Метр. Таблица единиц длины.

Задачи урока, направленные на формирование математической функциональной грамотности: развивать понимание необходимости математических знаний для учения и повседневной жизни; способствовать формированию математических знаний и умений.

На данном уроке целесообразно использование приема синтеза; задачи, связанные с величинами.

Примеры задач:

1. Сколько необходимо проволоки, чтобы огородить участок земли для огорода со сторонами 10 и 6 метров?

2. Со стены сняли старый плакат. Оказалось, что от клея на обоях осталось некрасивое пятно. Сторона квадрата – 50 см. Выбери, чем можно закрыть это пятно: карта мира -80 см * 45 см; плакат «таблица умножения» - 4 дм * 8 дм; репродукция картины – 30 см * 20 см; цветной календарь – 55 см * 6 дм?

3. Комната имеет пол прямоугольной формы со сторонами 5 м и 4 м. Высота 3 м. Сколько рулонов обоев необходимо купить. Используются обои шириной 50 см, длина рулона 10 м.

4. Комната имеет пол прямоугольной формы со сторонами 5 м и 4 м. Сколько плиток квадратной формы со стороной 50 см необходимо, чтобы сделать навесной потолок?

5. Размеры нашего класса 10 м и 6 м. Сколько метров линолеума необходимо купить для класса? Имеется в продаже линолеум шириной 1,5м и 2 м.

6. Твоя маленькая сестренка решила построить пирамидку, используя плоские фигуры квадратов и кругов, вырезанные из бумаги? Получится ли у нее? Почему? Попробуй объяснить ей, какие фигуры нужно использовать.

Решение данных задач направленно на формирование математической функциональной грамотности, а именно на развитие понимания необходимости математических знаний для учения и повседневной жизни.

Тема урока: Десяток. Устная нумерация чисел в пределах 100.

В данный урок мы включили решение дополнительных задач, таких как: развивать способность различать математические объекты, устанавливать математические отношения.

Для решения задач используем приёмы «Урок без темы», «дополни задачу».

Начало приема «Урок без темы» возможно со слов учителя: «Ребята, извините, но моя рука отказалась написать тему урока, и, кажется, неслучайно! Вот вам еще одна загадка, которую вы разгадаете уже в середине урока: почему рука отказалась записать тему урока?». Данный вопрос записывает в уголке классной доски.

Учитель: «Уважаемые ученики, вам предстоит проанализировать и доказать, с точки зрения полезности, отсутствие темы в начале урока! Но начинать урок нам все равно надо, и начнем с хорошо знакомого материала…». Данный прием мы можем использовать на многих уроках, посвященных закреплению того или иного материала, с целью непрерывного формирования математической функциональной грамотности.

Варианты задач с дополнением и развитие математической грамотности:

1. Дополни задачу таким числом, чтобы её можно было решить тремя способами. Реши задачу, составляя выражение.

В одной коробке было 6 карандашей, а в другой – 12 карандашей. Катя взяла карандашей. Сколько карандашей осталось в этих двух коробках?

В дальнейшем для пробации приёмов, направленных на формирование математической функциональной грамотности на уроках математики в образовательном учреждении, необходимы следующие условия:

1. учебный кабинет оснащен рабочим местом учителя начальных классов, оборудованным столом, шкафами для наглядных пособий, классной доской, инструментами и приспособлениями в соответствии со спецификой обучения младших школьников;

2. учебный кабинет также оснащен техническими средствами обучения, (компьютером и мультимедийным оборудованием), учебно-наглядными пособиями, необходимыми средствами обучения для организации образовательного процесса в начальных классах. все оборудование хранится таким образом, чтобы учитель в любой момент мог быстро найти и подготовить любой предмет учебного оборудования к использованию на уроке или во внеклассной работе;

3. планировка предполагает возможность изменяться в соответствии с использованием различных форм работы;

4. в классе создан благоприятный психологический климат, комфортная среда;

5. сформировано эмоционально – положительное отношение к урочной работе.

Указанные приёмы будут способствовать формированию математической функциональной грамотности у обучающихся, если будут соблюдены следующие условия:

1. включение всех учащихся в учебную деятельность;

2. установление доверительных отношений со всеми учащимися класса, основанных на взаимном уважении;

3. учет возрастных, индивидуальных особенностей, темпа работы младших школьников, типа восприятия развития внимания и памяти учащихся;

4. создание ситуации успеха для всех обучающихся через обеспечение условий работы как в зоне актуального. Так и в зоне ближайшего развития;

5. использование привлекательной и интересной для учащихся формы предъявления заданий.

Формы организации образовательного процесса:

1. фронтальная работа с классом (в основном при работе с заданиями, направленными на формирование каких – либо приемов, являющихся основными);

2. работа в группах и парах;

3. индивидуальная работа во время учебных занятий и после уроков);

4. самостоятельная работа на занятиях и дома по комплексу;

5. индивидуальные домашние задания.

Прогноз возможных негативных последствий:

1. Реализация продукта может вызывать трудности, связанные с недостаточным уровнем развития навыков исследовательских умений у обучающихся;

2. Трудности реализации комплекса заданий исследовательского характера во внеурочной деятельности в связи с низким уровнем развития математической грамотности у младших школьников;

3. Выход за временные рамки преддипломной практики из-за нехватки времени для реализации проекта.

Способы коррекции, компенсации негативных последствий.

Чтобы избежать возможных негативных последствий необходимо:

1. проанализировать программу по математике, чтобы включить в комплекс заданий задачи уже изученные младшими школьниками.

2. подобрать интересные, разнообразные, доступные для восприятия задания;

3. заинтересовать учащихся, предложив им принять участие в олимпиаде по математике, раскрыв сущность трех данных уровней компетентности, его цели, задачи, познакомить их с инструкцией по выполнению заданий, критериями оценки;

4. создать ситуацию успеха;

5. следовать четкому плану, грамотно распределять время для подготовки;

6. согласовать планируемую в процессе пробации деятельность с классным руководителем.

В целом можно сделать вывод о том, что цель данного проекта будет достигнута при грамотном применении приёмов, направленных на развитие математической функциональной грамотности у обучающихся на уроках математики. Гипотеза доказана, используя приёмы, направленные на формирование вычислительных приемов, повыситься уровень математической функциональной грамотности у детей младшего школьного. Результатом реализации выступает формирование математической функциональной грамотности второклассника.

Таким образом, применение предложенных приемов на уроках математики должны положительно повлияла на уровень развития математической грамотности учащихся 2 класса. Исходя из вышесказанного, можно сделать вывод, что разработанный педагогический проект и предложенные приемы, как средство развития математической грамотности младших школьников актуальны на сегодняшний день, поскольку в ходе его реализации у второклассников произойдут положительные изменения в развитии математической функциональной грамотности.

ВЫВОДЫ ПО ГЛАВЕ 2

В соответствии с поставленными задачами нами были подобраны методы диагностики для выявления уровня математической функциональной грамотности младших школьников: комбинированные диагностические работы для 2 класса разработанные Жидких Н. В. и Кокиной М. А. и работа, разработанная Локтиновой Натальей Васильевной.

Исследование уровня математической функциональной грамотности младших школьников было проведено на базе Муниципального бюджетного общеобразовательного учреждения средняя общеобразовательная школа № 90 (г. Нижний Тагил).

В исследовании приняли участие дети младшего школьного возраста, ученики 2 «А» класса. Общее количество опрошенных составило 22 человека в возрасте 8–9 лет, из них мальчиков – 11, девочек – 11.

При проведении диагностических комплексных работ, определили, что в классе в основном средний уровень математической функциональной грамотности. Это говорит о хорошей сформированности математических знаний по предмету и недостатке применения этих знаний в реальной жизни на практике.

В ходе создания проекта было определено проблемное поле и пути его решения: установление связей и интеграцию материала из разных математических тем, необходимого для решения поставленной проблемы; средний уровень развития математической функциональной грамотности у младших школьников.

Проанализировав полученные результаты, включили в программные уроки приёмы, направленные на формирование математической функциональной грамотности; подобрали интересные, разнообразные, доступные для восприятия задания.

ЗАКЛЮЧЕНИЕ

Одной из актуальных проблем современной начальной школы является формирование математической функциональной грамотности. Одним из показателей успешности вхождение в мировое образовательное пространство является выполнение образовательных международных стандартов, в которых формирование функциональной грамотности обозначено в качестве одной из приоритетных задач. Формирование функциональной грамотности — это условие становления динамичной и творческой, ответственной и конкурентоспособной личности.

В дипломной работе нам предстояло выявить и научно обосновать приемы, направленные на формирования математической функциональной грамотности у младших школьников на уроках математики.

Для решения данной цели перед нами был поставлен ряд задач:

1. На основе анализа психолого-педагогической и методической литературы изучить понятие «математическая функциональная грамотность» и ознакомиться с её признаками, структурой и уровнями развития;

2. Изучить психологические особенности детей младшего школьного возраста и определить особенности формирования математической функциональной грамотности в младшем школьном возрасте;

3. Выявить наиболее эффективные приемы формирования математической функциональной грамотности у младших школьников в процессе обучения;

4. Подобрать методики и описать результаты диагностики уровня сформированности математической функциональной грамотности;

5. Разработать педагогический проект, направленный на формирование математической функциональной грамотности у детей младшего школьного возраста.

В нашем исследовании мы выяснили, что функциональная грамотность – «способность человека решать стандартные жизненные задачи в различных сферах жизни и деятельности на основе прикладных знаний», а функционально грамотная личность — это человек, ориентирующийся в мире и действующий в соответствии с общественными ценностями, ожиданиями и интересами. Исходя из этого были выявлены составляющие математической функциональной грамотности младших школьников, такие как: критическое мышление, креативность, исследование и изучение саморегуляция, инициативность, настойчивость, использование информации, системное мышление, коммуникация и рефлексия.

Выяснили, что в ходе уроков математики развивается математическая культура учащихся в целом. В понятие математическая культура входят: алгоритмическая культура, вычислительная культура, графическая культура, логическая культура, математическая грамотность. Дополнительные задания, применяемые в системе на различных этапах урока, позволяют развивать различные компоненты математической грамотности. При решении задачи нами были выявлены наиболее эффективные условия формирования математической функциональной грамотности, такие как: создание информационно - развивающей образовательной среды; готовность учителя к реализации процесса — понимание им многоаспектности математической функциональной грамотности; поэтапное формирование математических умений и навыков от первого до четвертого класса; контроль над их формированием.

В рамках решения следующей задачи познакомились и изучили приёмы, направленные на формирования математической функциональной грамотности. Описали методику и результаты диагностики уровня сформированности математической функциональной грамотности; разработали педагогический проект, направленный на формирование математической функциональной грамотности у детей младшего школьного возраста.

Новизна выполненной выпускной квалификационной работы в сравнении с другими, родственными по тематике и целевому назначению заключается в том, что созданный педагогический проект представляет собой набор приёмов, последовательная реализация которых, способствует успешному формированию математической функциональной грамотности у младших школьников.

В заключении следует отметить, что используемые на уроках приёмы способствуют развитию информационно-образовательной среды, направленной на повышение математической функциональной грамотности учащихся, обеспечивающей личное саморазвитие, самостоятельность в приобретении знаний, формирующей коммуникативные навыки, умения использовать информацию и технологии, решать проблемы, предприимчивость и креативность.

Учитель должен увлечь и «заразить» детей, показать им значимость их деятельности и вселить уверенность в своих силах. При условии успешности решения поставленных задач мы выполним главную цель формирования функционально-грамотной личности т.е. формирование в общеобразовательных школах интеллектуального, физически и духовно развитого гражданина.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ И ИСТОЧНИКОВ

Законодательные и нормативные документы:

Закон «Об образовании в Российской Федерации» с изменениями и дополнениями на 2018 год [Текст]: федер. закон: [принят Гос. Думой 21 декабря 2012 г.: одобр. Советом Федерации 26 декабря 2012 г.] – М.: Проспект, 2018. – 110 с.

Концепция развития математического образования в Российской Федерации (утв. Распоряжением Правительства РФ от 24 декабря 2013 г. N 2506 р) — Режим доступа: https://docs.edu.gov.ru/document/

Национальный проект «Образование» (с 2019 до 2024 г.) Министерство просвещения Российской Федерации от 1.11.2018 г. — Режим доступа: https://edu.gov.ru/national-project

Приказ Рособрнадзора N 590, Минпросвещения России «Об утверждении методологии и критериев оценки качества общего образования в образовательных организациях на основе практики международных исследований качества подготовки обучающихся» N 219 от 06.05.2019 г. — Режим доступа: https://lp.vrtorg.ru/prikaz590

Федеральный государственный образовательный стандарт начального общего образования [Текст]: утвержден приказом Министерства образования и Науки Российской Федерации от 6 октября 2009 г., № 373, в ред. приказов от 26 ноября 2010 г. No 1241, от 22 сентября 2011 г. No 2357 / Министерство образования и науки Российской Федерации –М.: Просвещение, 2010. – 31 с.

Литература:

Алексеева,  Е. Е. Методика формирования функциональной грамотности учащихся в обучении математике [Текст] / Е. Е. Алексеева // Проблемы современного педагогического образования. - 2020. - No 66-2. - С. 10 - 15

Алхатова, Т. С. Компетенции педагога в использовании инновационных технологий в начальной школе в условиях обновленной системы образования [Текст] / Т. С. Алхатова, А. В. Семкин, Б. Н. Иманжанова // Наука и реальность. - 2020. - No 1. - С. 64-66.

Виноградова, Н. Ф. Концепция начального образования: «Начальная школа XXI века» [Текст] / Н. Ф. Виноградова. — М.: Вентана-Граф, 2017 — 64 с.

Виноградова, Н.Ф. Программа «Занимательная математика» // Сборник программ внеурочной деятельности: 1—4 классы [Текст] / под ред. Н. Ф. Виноградовой. — М.: Вентана-Граф, 2016. — 96 с.

Виноградова, Н.Ф. Функциональная грамотность младшего школьника: книга для учителя [Текст] / Н. Ф. Виноградова, Е. Э. Кочурова, М. И. Кузнецова и др.; под ред. Н. Ф. Виноградовой. — Москва: Российский учебник: Вентана-Граф, 2018. — 288 с.

Губанова М.И. Функциональная грамотность младших школьников: проблемы и перспективы формирования [Текст] /М. И. Губанова. —Начальная школа плюс до и после. – 2009. – No12. – С. 36-42.

Евтыхова Н.М., Багова Л.Л. / Формирование функциональной математической грамотности младших школьников средствам и межпредметной интеграции [Текст] // Вестник Майкопского государственного технологического университета. 2019. Вып. 4(43). С. 78-86.

Жумабаева, А. Е. Проблемы формирования функциональной грамотности учащихся начальных классов и пути их решения А. Е. Жумабаева, А. Б. Ы. Ы. Тоқан [Текст] / Образование в XXI веке: сборник материалов III Международной научно-практической конференции. – Москва, 2020. - С. 351-356.

Карачевцева, А. П.Формирование функциональной математической грамотности младшего школьника средствами интерактивной образовательной платформы "учи.ру" [Текст] / А. П. Карачевцева // Педагогический поиск. - 2019. - No 5. - С. 6-9.

Кларин, М. Педагогические технологии и инновационные тенденции в современном образовании (зарубежный опыт) [Текст] / М. Кларин//Инновационное движение в российском школьном образовании. -Москва, 2017. -.337 с.

Козлова, М. И. Повышение функциональной грамотности как необходимость современного образования [Текст] / М. И. Козлова // Сборник статей II Международного учебно-исследовательского конкурса. - Петрозаводск, 2020. - С. 116-125.

Леонтьев А. H., Деятельность. Сознание. Личность [Текст] / Н.А. Леонтьев. – М.: Политиздат, 1975. – 175 с.

Леонтьев, А.А. От психологии чтения к психологии обучения чтению [Текст] // Материалы 5‑й Международной научно-практической конференции (26–28 марта 2001 г.) : в 2 ч. — Ч. 1 / под ред. И.В. Усачевой. — М., 2002.

Перминова Л.М. Формирование функциональной грамотности учащихся: основы теории и технология [Текст] / Л.М. Перминова. – СПб., 2018. – С. 25.

Моро М.И., Бантова М.А., Бельтюкова Г.В. Математика. 2 класс. [Текст] / М. И. Моро, М. А. Бантова. — 6-е издание. — М.: Просвещение. – 2015 г. — 96 с.

Моро М.И., Бантова М.А., Бельтюкова Г.В. Математика. Методические рекомендации, 2 класс. [Текст] / М. И. Моро, М. А. Бантова. — 6-е издание. — М.: Просвещение. – 2018 г. — 89 с.

Медеубаева, К. Т. Педагогические условия формирования функциональной грамотности учащихся [Текст] / К. Т. Медеубаева // Социально-педагогическая поддержка лиц с ограниченными возможностями здоровья: теория и практика: сборник статей по материалам III Международной научно-практической конференции: в 2 частях. Гуманитарно-педагогическая академия ФГАОУ ВО «Крымский федеральный университет им. В. И. Вернадского». - 2019. - С. 63-66

Монахов, В.М. Педагогические аспекты интеграции педагогических технологий и информационных технологий как качественно новые этап информатизации математического образования[Текст] / Монахов В.М. Педагогика. 2016. С. 287-291

Семенова, И. В. Адаптивно-инновационные педагогические технологии в формировании функциональной грамотности школьников [Текст] / И. В. Семенова, О. А. Казарова; научный редактор Н. О. Берая // Избранные вопросы науки XXI века: сборник научных статей. - Москва, 2019. - С. 42-46.

Ушакова, М. А. Развитие функциональной грамотности школьников посредством повышения качества математического образования [Текст] / М. А. Ушакова // Научно-методическое обеспечение оценки качества образования. - 2020. - No 1 (9). - С. 56-59

Федорова, Е. И. Логическая грамотность – одно из направлений функциональной грамотности [Текст] / Е. И. Федорова // Современная образовательная среда: теория и практика: сборник материалов Всероссийской научно-практической конференции. ФГБОУ ВО «Чувашский государственный университет им. И.Н. Ульянова»; Актюбинский региональный государственный университет им. К. Жубанова. – Чебоксары, 2020. - С. 47-49.

Царегородцева, Е. А. Формирование когнитивного опыта как основы функциональной грамотности младших школьников [Текст] / Е. А. Царегородцева // Детство, открытое миру: сборник материалов Всероссийской научно-практической конференции с международным участием. - 2020. - С. 95-98.

«Особенности формирования функциональной грамотности учащихся основной школы при освоении дисциплин общественно-гуманитарного цикла» [Текст] / Методическое пособие. – Астана: Национальная академия образования им. И. Алтынсарина, 2013. – 40 с.

Источники из интернета:

Базарнова, Е. Н. Формы работы на уроках математики в процессе решения текстовых задач [Электронный ресурс] / Е. Н. Базарнова // Сайт «Фестиваль педагогических идей «Открытый урок»». – 2014. – Режим доступа: http://referatwork.ru/refs/pedagogics/ref-6148.html

Выготский, Л.С. Психология развития ребенка/Л.С.Выготский. –МоскваЭксмпо, 2004. – 310 с. [Электронный ресурс]. Режим доступа: https://bookap.info/deti/vygotskiy_psihologiya_razvitiya_rebenka/

Ковалева, Г.С. Возможные направления совершенствования общего образования для обеспечения инновационного развития страны (по результатам международных исследований качества общ его образования) [Электронный ресурс]. Режим доступа: http://www.centeroko.ru/public.htm l

Образовательная программа «Школа России» [Электронный ресурс]. Режим доступа: https://prosv.ru/umk/school-russia.html

Янгирова, В.М., Шамигулова, О.А. Методологические ориентиры профессиональной подготовки учителя к диагностике образовательных результатов // Современные проблемы науки и образования. – 2015. – № 5; [Электронный ресурс]. Режим доступа: http://www.science-education.ru/128-22221

Международная программа по оценке образовательных достижений учащихся. Информация об исследовании [Электронный ресурс]. Режим доступа: https://gtmarket.ru/research/pisa/info

Сборник тестовых заданий TIMSS. – АО «Информационно-аналитический центр»: Астана, 2016 - 175 с. [Электронный ресурс]. Режим доступа: http://iac.kz/sites/default/files/2_rus_var_arial_ot_ir_0.pdf

Сетевой комплекс информационного взаимодействия субъектов Российской Федерации в проекте «Мониторинг формирования функциональной грамотности учащихся» [Электронный ресурс]. Режим доступа: http://skiv.instrao.ru/

ЮНЕСКО. Акты генеральной конференции / 20-я сессия. – Париж, 1978. — [Электронный ресурс]. Режим доступа: https://psypress.ru/files/24566/resolution.pdf

ПРИЛОЖЕНИЕ 1

Комплексная диагностическая работа

Разработчики: Жидких Наталья Викторовна, Кокина Марина Алексеевна

Вариант 1

ИНСТРУКЦИЯ для УЧАЩИХСЯ Работа состоит из четырёх заданий, каждое задание описывает одну ситуацию. В каждом задании два вопроса. Таким образом, всего в работе 8 вопросов, на которые вам необходимо будет дать ответ. На выполнение работы отводится 40 минут. В работе вам встретятся задания с разной формой ответа. При ответе на вопрос с выбором ответа, нужно отметить ответ, который считаете верным, поставив знак «√». При ответе на вопрос с кратким ответом, записывайте ответ в специально отведенном месте после слов «Ответ», «числовое выражение». В работе есть вопросы, к которым нужно не только дать ответ, но и записать решение или объяснение. В этих заданиях написано: «запишите решение», «докажите», «объясните». Желаем успеха!

Выполните задания 1-4

Задание 1. Миша собирал машинку из конструктора, но её собрать не удалось, так как в коробке оказалось не 78 деталей, а 76.

Вопрос 1/1. Сколько деталей не хватало в конструкторе?

Числовое выражение: __________________________________________

Вопрос 1/2. Докажите, что 22 детали будет достаточно, чтобы дополнить бракованную партию конструкторов, в которой 10 таких коробок.

Объясните свой ответ.

Задание 2. Света и Наташа делают красивые украшения и выставляют на продажу в Интернете. За неделю они продают 2 браслета по 30 руб. и одну брошь за 50 руб.

Вопрос 2/1. Сколько девочки зарабатывают денег за неделю?

Браслет - 30 руб. Брошь - 50 руб.

Составь числовое выражение: ___________________________________

Вопрос 2/2 На сколько больше смогут девочки заработать денег за месяц, если за неделю смогут выполнять комплект из двух брошей и двух браслетов? Запиши ответ в таблицу.

	Цена одного изделия	Комплект 1	Комплект 2
Браслет	30 руб.	2 браслета	2 браслета
Брошь	50 руб.	1 брошь	2 броши
Стоимость комплекта
Сверхприбыль за месяц

Задание 3. Ярик и Сава ездят на тренировки в спорткомплекс «Атлет» на автобусе. Билет стоит 22 руб. Рассмотри достоинства монет.

Сава

Ярик

Вопрос 3/1. Какую сумму денег насчитал в своих карманах каждый из ребят?

Выбери правильный ответ.

1. 50 и 25

2. 42 и 25

3. 35 и 42

4. 50 и 35

Вопрос 3/2. Хватит ли обоим мальчикам денег на обратный проезд?

Объясни свой ответ.

______________________________________________________________

Задание 4. На графике показан доход семьи за один год по месяцам.

Вопрос 4/1. Рассмотри график и ответь на вопросы:

1. В каких месяцах доход семьи можно считать стабильным?

2. В каком месяце доход семьи был самым высоким? Самым низким?

3. В каком месяце доход семьи был выше: в июле или в октябре?

4. В каком месяце доход семьи был ниже: в апреле или в ноябре

1. __________________________________________________________

2. __________________________________________________________

3. __________________________________________________________

4. __________________________________________________________

Вопрос 4/2. На какие месяцы приходится постепенный рост дохода семьи?

Выбери правильный ответ.

1. С апреля по август

2. С июля по декабрь

3. С февраля по май

4. С января по март

Вариант 2.

З адание 1. Карандаш стоит 9 руб., а ластик 5 рублей.

9 руб. 5 руб.

Вопрос 1/1. Составьте числовое выражение, которое показывает, на сколько карандаш стоит дороже ластика?

Числовое выражение: _________________________________________

Вопрос 1/2. Докажите, что за 70 руб. можно купить 5 ластиков и 5 карандашей.

Объясните свой ответ.

_____________________________________________________________

Задание 2. Крот попросил мышь выдать Дюймовочке зёрнышки. Дюймовочке мышь выдала 6 зёрнышек, а кроту сказала, что 9.

Вопрос 2/1. Составьте числовое выражение, которое показывает, сколько зёрнышек мышь присвоила себе?

Числовое выражение: ________________________________________

Вопрос 2/2. Запишите в таблице, сколько зёрнышек сэкономит мышь за неделю.

	За 1 день	За неделю
Должна дать	9 зёрен
Дала по факту	6 зёрен
Сэкономила

Задание 3. Ольга и Светлана пошли в кино. Билет стоит 150 рублей. Оля расплатилась двумя 100- рублёвыми банкнотами, Светлана – одной номиналом в 500 рублей.

Вопрос 3/1. Какую сумму каждая из них получила на сдачу?

Выбери правильный ответ.

1. 50 и 250

2. 100 и 250

3. 50 и 100

4. 50 и 350

Вопрос 3/2. Сколько билетов могут купить девочки для своих подруг на полученную сдачу?

Ответ: _______________________________________________________

Объяснение: __________________________________________________

Задание 4. В соответствии с правилами регистрации юридических лиц за год было закрыто 40 кафе в связи с неуплатой налогов.

Вопрос 4/1. Определите по графику, в каком месяц было закрыто больше всего кафе, а в какой- меньше всего?

1. _________________________________________________________

2. _________________________________________________________

Вопрос 4/2. В какой период уплата налогов была стабильной. Обведи правильный ответ.

1) в апреле и мае?

2) в феврале или в марте?

ПРИЛОЖЕНИЕ 2

Комбинированная диагностическая работа для 2 класса по определению математической и финансовой грамотности (ФиМГ)

Разработчик: Локтионова Наталья Васильевна

Фамилия, имя____________________________учени___2 _____ класса

Математическая грамотность

1. Прочитай словесные формулировки и числовые выражения. Соедини линией.

К сорока прибавить тридцать три Уменьшаемое двадцать семь, вычитаемое 7 Сорок увеличить на тридцать три К тринадцать прибавить разность чисел двадцати двух и двенадцати Двадцать семь уменьшить на семь

27 -7 13+ (22 - 12) 40 +33

1. Дай название каждой группе

	34 56 100 18	метр дециметр сантиметр миллиметр	вычитание сложение

1. Прочитай. Соедини название величины и то, что удобно этой величиной измерить.

Метр час литр килограмм миллиметр

вес своего тела молоко в банке время, которое ты проводишь в школе длину ластика расстояние от твоего дома до соседнего дома

1. Прочитай.

Маша придумала 12 выражений со скобками, значение которых равно 18, а Катя придумала на 5 таких выражений больше.

Поставь вопрос и реши задачу.

Вопрос: ___________________________________________________

Решение: _________________________________________________

1. Прочитай.

У Вити 28 р. А у Маши 10 р.

Поставь вопрос и реши задачу.

Вопрос: ___________________________________________________

Решение: _________________________________________________

1. У Пети и Коли вместе 9р. У Пети денег больше. Сколько денег у Коли?

Запиши все возможные решения.

Решение:

1)________________________________________________________

2)________________________________________________________

3)________________________________________________________

4)________________________________________________________

1. Рассмотри рисунок и ответь на вопросы.

1. На сколько рублей сыр дешевле сока? ______________________

2. На сколько рублей сыр дороже творога? ____________________

3. На сколько рублей сок дороже конфет? _____________________

4. Какова стоимость конфет и сыра? ________________________

5. Какова стоимость творога и конфет? _____________________

1. Посчитайте, чему равны доход и расход семьи, если

- зарплата папы и мамы 75 рублей

- истратили на продукты 32 рубля

- заплатили за свет, интернет 12 рублей

- пенсия дедушки 20 рублей

- заплатили за ремонт компьютера 8 рублей

- купили новую кофту дочери – 5 рублей

Ответ:

1. доход семьи ____________________________________________

2. расход семьи____________________________________________

1. На графике показан доход семьи за один год по месяцам. Рассмотри графики ответь на вопросы:

1. В каких месяцах доход семьи можно считать стабильным (постоянный, одинаковый)? _______________________________

2. В каком месяце доход семьи был самым высоким? ____________

3. В каком месяце доход семьи был самым низким? _____________

4. В каком месяце доход семьи был выше: в июле или октябре? _______________________________________________________

5. В каком месяце доход семьи был ниже: в апреле или ноябре? _______________________________________________________

1. Мама расплачивалась 10 раз в неделю безналичными деньгами (банковской картой), 8 раз наличными деньгами. Какими деньгами чаще расплачивалась мама, безналичными или наличными?

Запиши неравенство. ________________________________

№ задания	Правильный ответ	Критерии оценивания
Математическая грамотность
1	К сорока прибавить тридцать три Уменьшаемое двадцать семь, вычитаемое 7 Сорок увеличить на тридцать три К тринадцать прибавить разность чисел двадцати двух и двенадцати Двадцать семь уменьшить на семь 27 -7 13+ (22 - 12) 40 +33	1 балл за каждый правильный ответ Максимальное количество баллов – 5 баллов
2	Геометрические фигуры Числа Величины Математи ческие действия 34 56 100 18 метр дециметр сантиметр миллиметр вычитание сложение	1 балл за каждый правильный ответ Максимальное количество баллов – 4 баллов
3	метр час литр килограмм миллиметр вес своего тела молоко в банке время, которое ты проводишь в школе длину ластика расстояние от твоего дома до соседнего дома	1 балл за каждый правильный ответ Максимальное количество баллов – 5 баллов
4	Варианты ответов Решение 1. Вопрос: Сколько выражение придумала Катя? Решение: 12+5=17 выражений Решение 2. Вопрос: На сколько больше (меньше) выражений придумала Катя (Маша), чем Маша (Катя)? Решение: 12+5=17 (выражений) придумала Катя 17-12=5 (выражений) Решение3. Вопрос: Сколько всего выражений придумали, катя и Маша? Ответ: 12+5=17 (выражений) придумала Катя 12+17=29 (выражений)	Записан вопрос -1 балл Записано решение задачи – 1 балл Максимальное количество баллов – 2 балла
5	Варианты ответов Решение 1. Вопрос: Сколько всего рублей у Вити и Маши? Решение: 28р+10р=38р (28+10=38) Решение 2. Вопрос: На сколько рублей у Вити (Маши) больше (меньше), чем у Маши (Вити)? Решение: 28р-10р=8 р (28-10=80)	Записан вопрос -1 балл Записано решение задачи – 1 балл Максимальное количество баллов – 2 балла
6	1+8=9 (8+1=9) 2+7=9 (7+2=9) 3+6=9 (3+6=9) 4+5=9 (5+4=9)	За каждое правильно записанное решение 1 балл Максимальное количество баллов – 4 балла
7	1) на 8 рублей (15-7=8) 2) на 1 рубль (7-6=1) 3) на 7 рублей (15-8=7) 4) 15 рублей (8+7=15) 5) 14 рублей (8+6=14)	За каждое правильно записанное решение 1 балл Максимальное количество баллов –5 баллов
ИТОГО 27 баллов
Финансовая грамотность
9	Ответы: 75 р + 20 р = 95 р 32 р +12 р +8 р + 5 р = 57 р	За каждый правильный ответ 1 балл Максимальное количество баллов –2 балла
10	Январь, февраль, март Декабрь Май В октябре В апреле	За каждый правильный ответ 1 балл Максимальное количество баллов –5 баллов
11	10 8, безналичными	За правильный ответ 1 балл Максимальное количество баллов –1 балл
ИТОГО 8 баллов