ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«МАГНИТОГОРСКИЙ ПЕДАГОГИЧЕСКИЙ КОЛЛЕДЖ»
(Магнитогорский педагогический колледж)
Отделение педагогическое
Кафедра психолого-педагогических дисциплин и частных методик
Формирование приема аналогии при обучении математике в начальных классах
Выпускная квалификационная работа
по специальности преподавание в начальных классах
Студента группы 741
очной формы обучения
Фахретдинова Асия Амировна
Руководитель: Сидорова
Мария Агановна
| Работа допущена к защите: _______________________ (руководитель) ___________________ (нормоконтролер) ___________________ (зав. кафедрой) «___» ______________ 20 г. | Работа защищена в ГАК с оценкой ___________________ Председатель ГАК __________ Члены ГАК _______________ ________________________ «___» ______________ 20 г.
|
Магнитогорск, 2017
Содержание.
Введение 3
I. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ФОРМИРОВАНИЯ ПРИЕМА АНАЛОГИИ ПРИ ОБУЧЕНИИ МАТЕМАТИКИ В НАЧАЛЬНЫХ КЛАССАХ. 7
1.1 Формирование логических универсальных учебных действий младших школьников. 7
1.2 Развитие мышления младших школьников с помощью логических приемов. 12
II. МЕТОДИЧЕСКИЕ АСПЕКСТЫ ИСПОЛЬЗОВАНИЯ ПРИЕМА АНАЛОГИИ ПРИ ИЗУЧЕНИИ НАЧАЛЬНОГО КУРСА МАТЕМАТИКИ 20
2.1. Использование приёма аналогия в современных программах начального обучения математике. 20
2.2 Методические рекомендации по использованию приема аналогии. 26
2.2.1 Аналогия при изучении законов арифметических действий. 26
2.2.2 Аналогия при формировании умений решать задачи. 29
2.3. Аналогия при изучении математических понятий 38
Заключение. 43
Приложение. 48
Введение
Изучение математики в школе направлено на достижение, в первую очередь, целей интеллектуального развития учащихся, формирования качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе, для общей социальной ориентации и решения практических проблем.
В сферу интересов личности входит умение адаптироваться к новым условиям жизни: анализировать ситуацию, адекватно изменять организацией свою деятельность, уметь владеть средствами коммуникации, добывать информацию и пользоваться ею. Если с этой точки зрения обратится к целям школьного математического образования, то одной из первоочередных и важнейших задач является развитие мышления учащихся. «Учить надобно не мыслям, а мыслить»,- эти слова немецкого философа и ученого И. Канта имеют большое значение, являются приоритетным принципом в обучении математике. Основной целью образовательного процесса становится усвоение определенных способов мышления, обеспечивающих понимание и производство новых знаний.
В последние годы много и часто говорят о недостаточной эффективности процесса обучения. Учителя озабочены тем, что школьники с трудом усваивают учебный материал, не могут применять знания в измененной ситуации, выбрать тот или иной метод решения задач.
Методы и приемы обучения младших школьников в процессе усвоения новых знаний неразрывно связаны с построением различных рассуждений. Любое рассуждение состоит из цепочки умозаключений. В математической логике выделяются основные виды умозаключений: дедуктивные, индуктивные и по аналогии. Умение строить умозаключения необходимо в ходе изучения любого предмета, однако на уроках математики формирование таких умений наиболее перспективно, что обусловлено абстрактным содержанием этого предмета. Необходимость строить умозаключения возникает на каждом этапе формирования математических понятий и представлений о них, в ходе анализа текстовых задач, при решении уравнений и т. д.
В условиях вариативности начального образования
большую роль при формировании логических универсальных учебных действий отводят математике. Поскольку в первую очередь, при обучении математике у учащихся развиваются такие свойства интеллекта, как:
- математическая интуиция (на методы решения задач, на образы, свойства, способы доказательства, построения);
- логическое мышление (понимание понятий и общепонятийных связей, владение правилами логического вывода, понимание и сохранение в памяти важных доказательств);
- пространственное мышление (построение пространственных абстракций, анализ и синтез геометрических образов, пространственное воображение);
- алгоритмическое мышление, необходимое для профессиональной деятельности в современном обществе;
- владение символическим языком математики (понимание математических символов, умение записывать в символической форме решения и доказательства);
- математические способности школьников (способности к абстрагированию и оперированию формальными структурами, обобщению).
Федеральный государственный стандарт начального общего образования выделяет такие виды универсальных учебных действий как личностные, регулятивные, познавательные и коммуникативные.
Универсальные учебные действия определяются как совокупность способов действия учащегося, обеспечивающий его способность к самостоятельному усвоению новых знаний и умений, включая организацию этого процесса.
Проблема эффективного формирования универсальных учебных действий учащихся – одна из сложных и противоречивых проблем современной педагогической науки. С одной стороны, она отражает потребность общества, выраженную в образовательном заказе на учащихся, способных к полноценной самореализации, самостоятельному добыванию знаний и эффективному осуществлению различного рода деятельности; отражает заинтересованность ученых в нахождении путей формирования надпредметных действий школьников. С другой стороны, показывает, что современная система школьного образования с традиционной организацией учебного процесса и соответствующим методическим обеспечением не готова справиться с объективными факторами, определяющими формирование общепознавательных действий учащихся, и грамотно, на научной основе, обеспечить формирование надпредметных действий младших школьников в оценочной деятельности.
Учебный предмет «Математика» занимает ведущее место в начальном обучении. Успехи в изучении математики во многом определяют качество подготовки ребенка по другим школьным предметам. В частности на уроках математики есть возможность наиболее эффективно организовать работу по формированию и развитию познавательных, регулятивных и коммуникативных универсальных действий.
Итак, именно математика, позволяет целенаправленно формировать логические универсальные действия и открывает возможности их систематического использования в различных предметных дисциплинах.
Исходя из этого, актуальностью исследуемой проблемы является то, что знание логики повышает культуру мышления, вырабатывает навык мыслить «грамотно», развивает критическое отношение к своим и чужим мыслям. А также «учит человека сознательно применять законы и формы мышления и на основе этого логичнее мыслить и, следовательно, правильнее познавать мир» - этим я обосновываю выбор темы «Формирование приема аналогии при обучении математики в начальных классах».[13]
Объект исследования – процесс обучения математике в начальных классах.
Предмет исследования – аналогии, используемые при обучении математике в начальных классах.
Цель исследования – проанализировать теоретические основы и разработать методические рекомендации по использованию аналогии в начальном курсе математики.
Задачи исследования:
-
Проанализировать психолого - педагогические основы формирования логических универсальных учебных действий младших школьников.
-
Рассмотреть особенности развития мышления младших школьников при использовании логических приемов.
-
Проанализировать современное состояние использования приема аналогии в начальном обучении математике.
-
Разработать методические рекомендации по использованию приема аналогии при обучении математике в начальных классах.
Методы исследования: изучение и анализ математической, методической, педагогической литературы, учебных программ, учебников, учебных пособий;
Структура: выпускная квалификационная работа состоит из введения, двух глав, заключения и списка использованных источников.
Теоретическая значимость: в ходе изучения и анализа математической, методической, педагогической литературы, учебных программ, учебников, учебных пособий я расширила современные представления о приеме аналогии;
Практическая значимость: заключается в том, что в ходе работы над ВКР мной было создано методическое пособие по использованию приемов аналогии в начальных классах;
- ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ФОРМИРОВАНИЯ ПРИЕМА АНАЛОГИИ ПРИ ОБУЧЕНИИ МАТЕМАТИКИ В НАЧАЛЬНЫХ КЛАССАХ.
|
| 1.1 Формирование логических универсальных учебных действий младших школьников. |
Обучение, по своей природе и по особенностям его организации процесс достаточно сложный. С одной стороны, оно предполагает вооружение учащихся суммой действенных знаний, то есть знаний, легко и сознательно применяемых в любой ситуации. Параллельно с этим и во взаимосвязи с ним идет другой, не менее важный, процесс формирования приемов учебного труда, определенных умений, дающих возможность учащимся усваивать знания легко и, более того, приобретать их самостоятельно. Фонд действенных знаний – это материал для формирования учебных умений; вместе с тем сформированные умения дают возможность пополнять этот фонд новыми знаниями.
Существует две категории учебных умений: общие и специальные. Речь пойдет об общеучебных умениях и навыках, которыми должен овладеть в ходе обучения любой учащийся
Универсальные учебные действия – это универсальные для многих школьных предметов способы получения и применения знаний, в отличие от предметных умений, которые являются специфическими для той или иной учебной дисциплины.
В широком значении термин «универсальные учебные действия» означает умение учиться, т. е. способность субъекта к саморазвитию и самосовершенствованию путем сознательного и активного присвоения нового социального опыта. В более узком (собственно психологическом) значении этот термин можно определить как совокупность способов действия учащегося (а также связанных с ними навыков учебной работы), обеспечивающих самостоятельное усвоение новых знаний, формирование умений, включая организацию этого процесса. [2]
В начальной школе предмет «Математика» является основой развития у учащихся логических универсальных учебных действий. Для успешного обучения в начальной школе должны быть сформированы следующие познавательные универсальные учебные действия: общеучебные, логические, действия постановки и решения проблем.
Рассмотрим логические универсальные действия, к ним относятся:
− анализ объектов с целью выделения признаков (существенных, несущественных);
− синтез, составление целого из частей, в том числе самостоятельное достраивание с восполнением недостающих компонентов;
− выбор оснований и критериев для сравнения, классификации объектов;
− подведение под понятие, выведение следствий; − установление причинно-следственных связей, представление цепочек объектов и явлений;
− построение логической цепочки рассуждений, анализ истинности утверждений;
− доказательство;
− выдвижение гипотез и их обоснование [1].
Анализ − это процесс разложения на составные части одного целого объекта или явления с целью его более подробного и тщательного изучения, а также выявления его природы и закономерностей; данный процесс является одним из самых эффективных среди других инструментов изучения определённого объекта или явления.
Синтез – соединение различных элементов, сторон объекта в единое целое систему, которое осуществляется как в практической деятельности, так и в процессе познания. В этом значении термин синтез противопоставляется анализу, с которым он неразрывно связан. Синтез и анализ дополняют друг друга, каждый из них осуществляется с помощью и посредством другого. Анализ и синтез лежат не только в основе всех видов человеческой деятельности, но в своих элементарных формах – в основе поведения высших животных. Синтез, как мыслительная операция, производен от предметного соединения частей объектов в целое и исторически формируется в процессе общественно-производственной деятельности людей.
Обобщение – логическая операция конструирования нового понятия с большим объёмом, чем данное (то есть переход от видового к родовому понятию). Обобщение происходит путём отбрасывания из содержания понятия основных признаков понятия до тех пор, пока не получится15 предельно широкое понятие , называемое категорией (время, пространство, форма, количество, отношение), или к неопределённому понятию, описываемому через категории.
Сравнение − операция сопоставления предметов с целью выявления их возможных отношений, способ выявления единства и разнообразия вещей.
Сериация − упорядочение предметов по некоему признаку - размеру, цвету и прочее.
Классификация – процесс группировки объектов исследования или наблюдения в соответствии с их общими признаками. В результате разработанной классификации создаётся классифицированная система (часто называемая так же, как и процесс – классификацией).
Аналогия − сходство предметов (явлений, процессов и т. д.) в каких- либо свойствах. Сходство сопряжено с различием и без различия не существует. А всегда является попыткой продолжить «сходство несходного», причем продолжить его в новом, неизвестном направлении [3]. При умозаключении по аналогии (сходство) знание, полученное из рассмотрения какого-либо объекта («модели»), переносится на другой, менее изученный (менее доступный для исследования, менее наглядный и т. п.) в каком-либо смысле, объект. По отношению к конкретным объектам заключения, получаемые по аналогии (сходство), носят, вообще говоря, лишь вероятный характер; они являются одним из источников научных гипотез, индуктивных рассуждений и играют важную роль в научных открытиях. Если же выводы по аналогии (сходство) относятся к абстрактным объектам, то они при определённых условиях (в частности, при установлении между ними отношений изоморфизма или гомоморфизма) могут давать и достоверные заключения [19]. Аналогию дающую высоковероятное знание, принято называть строгой или точной. Научные аналогии обычно являются строгими [3].
Учебный предмет «Математика» имеет большие потенциальные возможности для формирования всех видов учебных универсальных действий: личностных, познавательных, коммуникативных и регулятивных. Реализация этих возможностей на этапе начального математического образования зависит от способов организации учебной деятельности младших школьников. Они учитывают потребности детей в познании окружающего мира и научные данные о центральных психологических новообразованиях младшего школьного возраста, формируемых на данной ступени: словесно-логическое мышление, произвольная смысловая память, произвольное внимание, планирование и умение действовать во внутреннем плане, знаково-символическое мышление, с опорой на наглядно - образное и предметно - действенное мышление.
В курсе «Математика» реализация этих возможностей обеспечивается системно-деятельностным подходом и методической концепцией курса, которая выражает необходимость систематической работы над развитием мышления всех учащихся в процессе усвоения предметного содержания.
Основным средством формирования универсальных учебных действий в курсе математики являются вариативные по формулировке учебные задания (объясни, проверь, оцени, выбери, сравни, найди закономерность, верно ли утверждение, догадайся, наблюдай, сделай вывод и т. д.), которые нацеливают обучающихся на выполнение различных видов деятельности, формируя тем самым умение действовать в соответствии с поставленной целью.
Следует помнить, что при формировании логических универсальных учебных действий необходимо обращать внимание на установление связей между вводимыми учителем понятиями и прошлым опытом детей, в этом случае ученику легче увидеть, воспринять и осмыслить учебный материал.
Предполагается, что результатом формирования логических универсальных учебных действий будут являться умения:
− произвольно и осознанно владеть общим приемом решения задач;
− осуществлять поиск необходимой информации для выполнения учебных заданий;
− использовать знаково-символические средства, в том числе модели и схемы для решения учебных задач;
− ориентироваться на разнообразие способов решения задач;
− учиться основам смыслового чтения художественных и логических текстов; уметь выделять существенную информацию из текстов разных видов;
− уметь осуществлять анализ объектов с выделением существенных и несущественных признаков
− уметь осуществлять синтез как составление целого из частей;
− уметь осуществлять сравнение и классификацию по заданным критериям;
− уметь устанавливать причинно-следственные связи;
− уметь строить рассуждения в форме связи простых суждений об объекте, его строении, свойствах и связях;
− уметь устанавливать аналогии;
− владеть общим приемом решения учебных задач;
− осуществлять расширенный поиск информации с использованием ресурсов библиотеки, образовательного пространства родного края (малой родины);
− создавать и преобразовывать модели и схемы для решения задач;
− уметь осуществлять выбор наиболее эффективных способов решения образовательных задач в зависимости от конкретных условий;
Конкретизируем содержание логических универсальных учебных действий, которые формируются на уроках математики:
− осознание, что такое свойства предмета;
– общие, различные, существенные, несущественные, необходимые, достаточные;
− моделирование;
− использование знаково-символической записи математического понятия;
− овладение приёмами анализа и синтеза объекта и его свойств;
− использование индуктивного умозаключения;
− выведение следствий из определения понятия;
− умение приводить контрпримеры.
Одно из важнейших логических универсальных действий:
− умение решать проблемы или задачи [18].
Усвоение общего приёма решения задач в начальной школе базируется на сформированности логических операций – умении анализировать объект, осуществлять сравнение, выделять общее и различное, осуществлять классификацию, логическую мультипликацию (логическое умножение), устанавливать аналогии.
1.2
Развитие мышления младших школьников с помощью логических приемов.
Современный уровень развития общества и соответственно сведения, почерпнутые из различных источников информации, вызывают потребность уже у младших школьников вскрыть причины и сущность явлений, объяснить их, то есть отвлеченно мыслить.
Мышление – это опосредованное и обобщённое отражение действительности, вид умственной деятельности, заключающейся в познании сущности вещей и явлений, закономерных связей и отношений между ними [12].
Мышление совершается по законам, общим для всех людей, вместе с тем в мышлении проявляются возрастные и индивидуальные особенности человека.
Многие авторы признают, что для умственного развития существенное значение имеет овладение системой знаний и мыслительными операциями (А. Н. Леонтьев, В.С.Шардаков, Н.И. Гребцова и др.), интеллектуальными умениями (П.Я. Гальперин, Н. А. Менчинская, А.Е. Вохмянина и др.), приемами умственной деятельности (А.З.Зак, Л.М. Фридман и др.). Однако вопрос о влиянии приемов мышления на умственное развитие учащихся (особенно младшего школьного возраста) остается не до конца решенным.
Первая особенность мышления - его опосредованный характер. То, что человек не может познать прямо, непосредственно, он познаёт косвенно, опосредованно: одни свойства через другие, неизвестное - через известное. Мышление всегда опирается на данные чувственного опыта – ощущения, восприятия, представления - и на ранее приобретённые теоретические знания. Косвенное познание и есть познание опосредованное.
Вторая особенность мышления - его обобщённость. Обобщение как познание общего и существенного в объектах действительности возможно потому, что все свойства этих объектов связаны друг с другом. Общее существует и проявляется лишь в отдельном, в конкретном.
Мыслительная деятельность человека представляет собой решение разнообразных мыслительных задач, направленных на раскрытие сущности чего-либо. Мыслительная операция – это один из способов мыслительной деятельности, посредством которого человек решает мыслительные задачи.
Мыслительные операции разнообразны. Это - анализ и синтез, сравнение, абстрагирование, конкретизация, обобщение, классификация и аналогия. Какие из логических операций применит человек, это будет зависеть от задачи и от характера информации, которую он подвергает мыслительной переработке.
В психологической науке различают такие формы мышления, как:
– понятия;
– суждения;
– умозаключения [16].
Понятие – это форма мышления, в которой отражаются общие и притом существенные свойства предметов и явлений. Каждый предмет, каждое явление имеют много различных свойств, признаков. Эти свойства, признаки можно разделить на две категории – существенные и несущественные.
Содержание понятий раскрывается в суждениях, которые всегда выражаются в словесной форме – устной или письменной, вслух или про себя. Суждение – основная форма мышления, в процессе которой утверждаются или отрицаются связи между предметами и явлениями действительности. Суждение – это отражение связей между предметами и явлениями действительности или между их свойствами и признаками. Суждение – это форма мышления, содержащая утверждение или отрицание какого-либо положения относительно предметов, явлений или их свойств. [17]
Из суждений также вытекают умозаключения. Умозаключение – это такая форма мышления, в процессе которой человек, сопоставляя и анализируя различные суждения, выводит из них новое суждение.
Различают следующие виды умозаключение: индуктивное, дедуктивное, по аналогии. [23]. Рассмотрим более подробно последний вид.
Под аналогией понимается особый вид умозаключения (рассуждения), когда от сходства двух объектов в некоторых признаках и при наличии дополнительного признака у одного из них делается вывод о наличии такого же признака у другого объекта.
Аналогия — это такой метод научного исследования, с помощью которого от сходства объектов данного класса в одних признаках делают вывод об их сходстве в других признаках. Суть аналогии можно выразить с помощью формулы:
А - имеет признаки a, b, c, d.
В - имеет признаки а, b, с.
Следовательно, В, по-видимому, имеет признак d.
Иначе говоря, в аналогии мысль исследователя идет от знания известной общности к знанию такой же общности, или, другими словами, — от частного к частному.
Для повышения вероятности выводов по аналогии необходимо стремиться к тому, чтобы было схвачено и выражено действительное, а не кажущееся сходство сопоставляемых объектов. Желательно, чтобы эти объекты были подобны в важных и существенных признаках, а не в случайных и второстепенных деталях. Полезно также, чтобы круг совпадающих признаков был как можно шире. Но наиболее важен для строгости аналогии характер связи сходных признаков предметов с переносимым признаком. Информация о сходстве должна быть того же типа, что и информация, распространяемая на другой предмет. Если сходное знание внутренне связано с переносимым признаком, вероятность вывода заметно возрастает. И наконец, при построении аналогии следует учитывать не только сходные черты сопоставляемых объектов, но и их различия. Если последние внутренне связаны с признаком, который предполагается перенести с одного объекта на другой, аналогия окажется маловероятной [3].
Формируя у школьников, умение выполнять умозаключения по аналогии, необходимо иметь в виду следующее:
а) аналогия основывается на сравнении;
б) для использования аналогии необходимо иметь два объекта, один из которых известен учащимся, а второй сравнивается с ним по каким-либо признакам;
в) для ориентации учащихся на использование аналогии необходимо в доступной для них форме разъяснить сущность последней, обратив внимание на то, что в математике нередко новый способ вычислений, преобразований можно открыть по догадке, внимательно изучив известный способ деятельности и данное новое задание;
г) для правильного вывода по аналогии сравниваются признаки объектов, существенные в данной ситуации, на что необходимо сориентировать учащихся.
А то вывод может быть неверным.
Метод аналогии дает наиболее ценные результаты тогда, когда устанавливается взаимосвязь не только между сходными признаками, но и с тем признаком, который переносится на исследуемый объект.
В обучении математике аналогия может быть использована при изучении свойств объектов, отношений между ними и действий с ними.
Аналогия свойств. В этом случае использование аналогии позволяет вскрывать некоторые новые свойства изучаемых объектов.
Например, переместительный закон: а + (b + c) = (a + b) + c.
2 + (15 + 9) = (2 + 15) + 9. Таким образом, от перестановки мест слагаемых, сумма не меняется.
Это и будет выводом по аналогии, в котором фиксируется определенное свойство вновь изучаемого объекта.
Аналогия отношений. Задание: сравнить 6 * (5 + 4) и 6 * 5 + 6 * 2.
Применяя знание смысла умножения, устанавливаем что
6 * (5 + 4) 6 * 5 + 6 * 2.
Сравниваем левую и правую части. Подмечаем, что 6 умножаем не на 4, а на 2.
Теперь возьмем выражение 3*(8+9) и 3*8+3*7.
По аналогии высказываем догадку, что 3*(8+9) 3*8+3*7
Проверка высказывания может быть проведена либо путем вычислений, либо путем рассуждений.
Аналогия действий. Здесь аналогия выражена в выводе о способе действия на основании изучения сравниваемого объекта.
Чтобы сделать вывод о способе сложения многозначного числа и однозначного, надо вспомнить, как сложить двузначное и однозначное:
24 + 7, 260 + 33, 4327 + 164 и на основе этих примеров, сделать вывод о сложении многозначного числа и однозначного.
Аналогия в деятельности учащихся может стать приемом, который будет помогать им, открывать новые знания, способы деятельности.
Аналогия – средство активизации учебно-воспитательной деятельности.
Приведем пример рассуждения по аналогии на материале начального курса математики.
При обучении делению на однозначное число используется такой прием. Сначала выясняется: чтобы найти значение выражения 12 : 4, следует узнать, на какое число надо умножить делитель 4, чтобы получить делимое, то есть 12. Известно, что 4 * 3 = 12. Значит, 12 : 4 = 3.
Затем учащимся предлагается, рассуждая так же найти, например, частное, 8 : 4. И они сначала находят число, на которое надо умножить 4, чтобы получить 8. Получают число 2 и делают вывод, что 8 : 4 = 2.
Далее, используя тот же способ рассуждений, находят частные 9:3,
20 : 5 и др.
Аналогия помогает открывать новые знания, способы деятельности или использовать усвоенные способы действия в измененных условиях.
Вывод при аналогии носит характер предположения, гипотезы и поэтому нуждается либо в доказательстве, либо в опровержении.
Широко используется аналогия в обучении математике младших школьников. Это происходит при изучении свойств объектов, отношений между ними и действий с ними. Например, если при изучении классов установлено, что в классе единиц 3 разряда − единицы, десятки, сотни, а в классе тысяч – тоже 3 разряда – единицы тысяч, десятки тысяч, сотни тысяч, то вывод о числе разрядов в классе миллионов и их названии дети могут сделать самостоятельно, по аналогии. То есть аналогию можно использовать для открытия «новых» свойств изучаемых объектов.
Аналогия может быть использована для установления отношения между данными объектами,. Например, учащиеся установили, что
2 · (9 + 7) 2 · 9 + 2 · 6 так как 2 · (9 + 7) = 2 · 9 + 2 · 7.
Рассматривая затем выражения 3·(8 + 9) 3 · 8 + 3 · 7, учащиеся могут по аналогии сделать вывод о том, что 3· (8 + 9) 3 · 8 + 3 · 7. Проверить его правильность можно либо путем рассуждений, аналогичных тем, что проводились при выполнении первого задания, либо при помощи вычисления.
Аналогия может быть использована и для выводов о способе действия на основе изучения другого способа. Так после рассмотрения способа умножения двузначного числа на однозначное, на примере умножения 27 и 3
(27 · 3 = (20 + 7) · 3 = 20 · 3 + 7 · 3 = 81) детям предлагается умножить 712 на 4. Действуя по аналогии; они устанавливают, что:
712 · 4 = (700 + 10 + 2) ·4= 2800 + 40 + 8 = 2848.
Далее по аналогии устанавливают способ умножения числа 6283 на 5. Следующим шагом может быть обобщение, то есть получение правила умножения многозначного числа на однозначное, то есть использование неполной индукции.
Таким образом, в процессе обучения младших школьников математике необходимо выполнять такие виды умозаключений, как дедуктивные, индуктивные и аналогию.
В математике аналогия различается на:
-
простую аналогию, при которой по сходству объектов в некоторых признаках заключают их сходство в других признаках;
-
распространенную аналогию, при которой из сходства явлений делают вывод о сходстве причин.
В свою очередь, простая и распространенная аналогия может быть:
1) строгой аналогией, при которой признаки сравниваемых объектов находятся во взаимной зависимости;
2) нестрогой аналогией, при которой признаки сравниваемых объектов не находятся в явной взаимной зависимости [24].
Аналогия является, пожалуй, одним из самых распространенных методов научного исследования. Широкое применение аналогий часто приводит исследователя к более или менее правдоподобным предположениям о свойствах изучаемого объекта, которые могут быть затем подтверждены или опровергнуты опытом или более строгими рассуждениями.
В данной главе мы рассмотрели формирование логических учебных универсальных действий младших школьников. Термин «универсальные учебные действия» означает умение учиться, то есть способность субъекта к саморазвитию и самосовершенствованию путем сознательного и активного присвоения нового социального опыта. А так же в составе основных видов универсальных учебных действий, соответствующих ключевым целям общего образования, выделяют четыре блока:
1) личностный;
2) регулятиный (включающий также действия саморегуляции);
3) познавательный;
4) коммуникативный [14].
При использовании аналогии совершается сложный мыслительный процесс, в обучении, как, впрочем, и в науке, аналогия часто полезна тем, что она наводит нас на догадки, то есть служит эвристическим методом. В обучении же математике не менее важно, чем учить доказывать, это учить догадываться, что именно подлежит доказательству и как найти это доказательство.
В данной главе мы рассмотрели развитие мышления младших школьников по средством логических приемов. И пришли к выводу что: мышление - это такая теоретическая и практическая деятельность, предполагающая систему включенных в нее действий и операций ориентировочно – исследовательского и познавательного характера.
- МЕТОДИЧЕСКИЕ АСПЕКСТЫ ИСПОЛЬЗОВАНИЯ ПРИЕМА АНАЛОГИИ ПРИ ИЗУЧЕНИИ НАЧАЛЬНОГО КУРСА МАТЕМАТИКИ
- Использование приёма аналогия в современных программах начального обучения математике.
Проанализировав УМК системы «Перспектива», мы выявили, что аналогия используется следующим образом.
Использование аналогии при изучении арифметического материала
1. Табличные случаи умножения и деления лежат в основе умножения и деления круглых чисел (с использованием знания разрядного состава чисел):
а) умножение и деление чисел, оканчивающихся нулями (на основе разрядного состава числа):
Умножение чисел оканчивающихся нулями в учебниках Дорофеева даются следующим образом:
20 * 3 = 60 20 * 3 = 60
20 + 20 + 20 = 60 20 дес. * 3 = 6 дес. = 60
1-й способ:
Чтобы 20 умножить на 3, можно 20 взять слагаемым 3 раза. Получим 60. Записываю так:
20 * 3 = 20 + 20 + 20 = 60
2-й способ:
20 – это два десятка. Поэтому чтобы 20 умножить на 3, можно 2 десятка умножить на 3. Получится 6 десятков или 60. Записываю так:
2 дес. * 3 = 6 дес. = 60.
Также в учебниках даются следующие примеры на умножение чисел оканчивающихся нулями, в которых мы видим использование приема аналогии, например:
Выполни вычисления по образцу:
| 20 * 4 = 80 |
| 200 * 4 = 800 |
| 2 дес. * 4 = 8 дес. = 80 | 2 сот. * 4 = 8 сот. = 800 |
30 * 2 10 * 4 20 * 5 100 * 8 300 * 3 200 * 2
Деление чисел оканчивающихся нулями в учебниках Дорофеева даются следующим образом:
60 : 3 = 20
6 дес. : 3 = 2 дес. = 20
60 – это 6 десятков. Поэтому, чтобы 60 разделить на 3, можно 6 десятков разделить на 3. Получится 2 десятка или 20. Записываю это так:
6 дес. : 3 = 2 дес. = 20.
Также в учебниках даются следующие примеры на деление чисел оканчивающихся нулями, в которых мы видим использование приема аналогии:
| 80 : 2 = 40 |
| 600 : 2 = 300 |
| 8 дес. : 2 = 4 дес. = 40 |
| 6 сот. : 2 = 3 сот. = 300 |
20 : 2 60 : 3 80 : 4 400 : 4 200 : 5 300 : 3
б) умножение на круглое число (на основе разрядного состава числа и сочетательного свойства умножения):
17 * 20 = 17 * (2 * 10) = (17 * 2) * 10 = 34 * 10 = 340
13 * 30 = 13 * (3 * 10) = (13 * 3) * 10 = 39 * 10 = 390
в) деление на круглые числа:
240 : 30 = 240 : (10 * 3) = 240 : 10 : 3 = 8
360 : 40 = 360 : (10 * 4) = 360 : 10 : 4 = 9
2. Письменные приемы сложения, вычитания, умножения, деления начинают изучать с простых случаев:
а) письменный прием сложения начинают изучать с простых случаев, например: 60 + 24 =
сперва учащимся показывают и проговаривают алгоритм записи:
+ 60 записываем единицы под единицами, десятки под десятками.
-
Слева ставим знак сложения (+), под примером проводим черту.
После записи знакомят с алгоритмом сложения. Складывать начинаем с единиц. 0+4=4 записываем ответ под единицами. Затем складываем десятки 6+2=8 записываем ответ под десятками. Читаем ответ 84.
Затем учащимся даются примеры аналогичные этому и они опираясь на образец решают остальные примеры.
+ 160 + 160 + 6160 + 6160
24 624 624 2624
б) следующий простой случай это письменные приемы вычитания, дается пример: 56-23=
Сначала учащимся показывают и проговаривают алгоритм записи: записываем единицы под единицами, десятки под десятками.
-56 Слева ставим знак вычитания (-), под примером проводим черту.
23 Вычитать начинаем с единиц, 6-3=3 ответ записываем под чертой, под единицами. Затем вычитаем десятки: 5-2=3 ответ записываем под десятками. Читаем ответ 33.
-56
23
33
Затем учащимся даются примеры аналогичные этому и они опираясь на образец решают остальные примеры.
- 556 - 556 - 1556 - 1556
23 323 323 1323
в) письменные приемы умножение даются с умножения на однозначное число. Например: 12 * 3 =
Детям объясняют что записываем пример мы также как сложение или вычитание, т.е. единицы под единицами, десятки под десятками. Затем также слева ставится знак умножения (х) и под примером проводится черта.
| * 12 | Умножение начинается с единиц, 2 * 3 = 6 ответ записываем под |
| 3 | единицами, после черты. Затем умножаем десятки 1 * 3 = 3, ответ |
| 36 | записываем под десятками, после черты. Читаем ответ 36. |
Затем учащимся даются примеры аналогичные этому и они опираясь на образец решают остальные примеры.
* 12 * 312 * 312 * 2312 * 2312
23 23 123 123 5123
г) письменные приемы деление начинают изучать с простого случая т.е. с деления на однозначное число, например: 48 : 4 =
При знакомстве с письменным делением учащихся знакомят с новым оформлением «уголком». Объясняют, что сперва мы рисуем уголок, делимое записываем слева, делитель справа над чертой, а частное под чертой. Промежуточные результаты записываются под делимым.
| - 48 | 4 | После записи компонентов деления, начинается само деление |
| 4 | 12 | делить начинаем с десятков: 4:4=1, записываем 1 в частном, |
| -8 |
| выполняем проверку 4 * 1 = 4, записываем промежуточный |
| 8 |
| результат под делимым. 4-4=0, остатка нет. Переходим к |
| 0 |
| делению единиц, сносим вниз 8 единиц, 8:4=2, записываем 2 в |
частном, выполняем проверку 4*2=8, записываем промежуточный результат под делимым. 8-8=0, остатка нет записываем 0 под чертой, деление окончено. Читаем ответ 12.
Затем учащимся даются примеры аналогичные этому и они опираясь на образец решают остальные примеры.
| 48 | 24 |
| 648 | 24 |
| 648 | 324 |
|
|
| 48 | 2 |
|
|
|
|
|
|
|
|
| 0 |
|
|
|
|
|
|
|
|
|
3. Свойство прибавления числа к сумме, усвоенное для случаев:
34 + 20 = (30 + 4) + 20 = (30 + 20) + 4 = 50 + 4 = 54,
34 + 5 = (30 + 4) + 5 = 30 + (4 + 5) = 30 + 9 + 39,
может быть использовано при вычислениях вида:
37 + 25 = (30 + 7) + (20 + 5) + (30 + 20) + (7 +5) = 50 + 12 = 62
4. Умножение и деление многозначного числа на однозначное выполняется по аналогии с умножением (делением) двузначного числа на однозначное (на основе разрядного состава числа и распределительного закона умножения (деления) относительно сложения):
24 ∙ 3 = (20 + 4) ∙ 3 = 20 ∙ 3 + 4 ∙ 3 = 60 + 12 = 72
69 : 3 = (60 + 9) : 3 = 60 : 3 + 9 : 3 = 20 + 3 = 23
418 ∙ 3 = (400 + 10 + 8) ∙ 3 = 400 ∙ 3 + 10 ∙ 3 + 8 ∙ 3 = 1200 + 30 + 24 = 1254
8408 : 4 = (8 000 + 400 + 8) : 4 = 8000: 4 + 400 : 4 + 8 : 4 = 2000 + 100 + 2 = 2102
5. Умножение многозначных чисел опирается на умножение многозначного числа на однозначное (на основе разрядного состава числа и распределительного закона умножения относительно сложения):
16 ∙ 12 = 16 ∙ (10 + 2) = 16 ∙ 10 + 16 ∙ 2 = 160 + 32 = 192;
286 ∙ 374 = 286 ∙ 300 + 286 ∙ 70 + 286 ∙ 4 = 85800 + 20020 + 1144 = 106964;
Здесь можно ограничиться планом решения, так как это подготовка к письменным приёмам умножения.
Использование аналогии при изучении геометрического материала
-
Сравни фигуры.
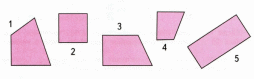
-В чем их сходство?
-Среди данных четырехугольников найди такие, у которых: а) один угол прямой; б) два прямых угла; в) четыре прямых угла;
-Фигуры под номером 2 и 5 называют прямоугольниками.
Прямоугольник - это четырехугольник, у которого все углы прямые.
Подумай, почему им дали такое название.
Посмотри на рисунок 2. Попробуй делением фигур на две группы, дать определение квадрата.
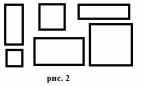
-Сравни свое определение с таким:
Квадрат – это прямоугольник, у которого все стороны равны.
-Определения похожи? Если не похожи, то чем?
-Найди в окружающем пространстве предметы, имеющие форму квадрата.
-
Начерти в тетради такие фигуры и дополни их до квадрата как показано в образце.
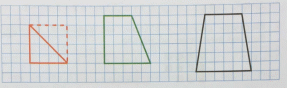
-
Раздели четвертый квадрат, используя соответствующую закономерность.
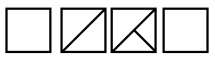
Раздели четвертый круг, используя соответствующую закономерность.
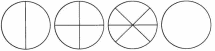
2.2 Методические рекомендации по использованию приема аналогии. 2.2.1 Аналогия при изучении законов арифметических действий.
Изучение и усвоение учащимися законов арифметических действий является неотъемлемой частью обучения математике в начальных классах. Знание конкретного смысла арифметических действий, взаимосвязи их компонентов и результатов, а также законов арифметических действий является одним из основных требований программы математики начальной школы.
Каждое из четырех арифметических действий должно прочно связаться в сознании детей с теми конкретными задачами, которые требуют его применения. Смысл действий и раскрывается главным образом на основе практических действий с множествами предметов и на системе соответствующих текстовых задач. На их основе доводится до сознания детей связь между компонентами и результатами действий, связь между действиями, свойства действий и изучаемые математические отношения.
В курсе математики начальной школы изучаются коммутативное (переместительное) и ассоциативное (сочетательное) свойства сложения и умножения, а также дистрибутивное (распределительное) свойство умножения относительно сложения и вычитания.
Переместительное свойство умножения широко используется при составлении таблицы умножения однозначных чисел. Сочетательный закон в начальной школе в явном виде не рассматривается, но используется вместе с переместительным законом при умножении числа на произведение. Распределительный закон умножения относительно сложения рассматривается в школе на конкретных примерах и носит название правил умножения числа на сумму и суммы на число. Рассмотрение этих двух правил диктуется методическими соображениями.
При формировании у младших школьников знания свойств арифметических действий также может быть использован прием аналогии.
Например, аналогия может использоваться при изучении переместительного свойства сложения. Для этой цели учащимся сначала предлагается найти значения выражений:
6+3 7+4 8+4
3+6 4+7 4+8
– Каким свойством вы воспользовались при выполнении задания? (Переместительным свойством сложения).
– Подумайте: как установить, выполняется ли переместительное свойство для умножения?
Учащиеся по аналогии записывают пары произведений и находят значение каждого, заменяя произведение суммой.
Для правильного умозаключения по аналогии необходимо выделить существенные признаки объектов, в противном случае вывод может оказаться неверным. Например, некоторые учащиеся пытаются применить способ умножения числа на сумму при умножении числа на произведение. Это говорит о том, что существенное свойство данного выражения – умножение на сумму, оказалось вне их поля зрения.
Формируя у младших школьников умение, выполнять умозаключения по аналогии, необходимо иметь в виду следующее:
• Аналогия основывается на сравнении, поэтому успех ее применения зависит от того, насколько ученики умеют выделять признаки объектов и устанавливать сходство и различие между ними.
• Для использования аналогии необходимо иметь два объекта, один из которых известен, второй сравнивается с ним по каким–либо признакам. Отсюда, применение приема аналогии способствует повторению изученного и систематизации знаний и умений.
• Для ориентации школьников на использование аналогии необходимо в доступной форме разъяснить им суть этого приема, обратив их внимание на то, что в математике нередко новый способ действий можно открыть по догадке, вспомнив и проанализировав известный способ действий и данное новое задание.
• Для правильных действий по аналогии сравниваются признаки объектов, существенные в данной ситуации. В противном случае вывод может быть неверным.[15]
С целью формирования у младших школьников приема аналогии можно предложить следующие задания:
– предлагать образец и требовать выполнения задания в точности по образцу;
– предлагать задания, в котором даётся образец и требуется выполнить задание по аналогии с образцом, но в измененных условиях;
– предлагать задания, не требующие вычислений;
– составлять задачу, аналогичную данной;
– проводить рассуждение при решении задачи по аналогии с решением сходной задачи.
Рассмотрим некоторые задания:
1.Выполните умножение, работая по образцу:
65 · 4 = (60 +5) · 4 = 60 · 4 + 5 · 4 = 240 + 20 = 260
81· 4 98 · 3 72 · 6 56 · 7
2. Вспомните, как умножить двузначное число на однозначное:
27 · 3 = (20 +7)· 3 = 20· 3 + 7· 3 = 60 + 21 = 81
По данному образцу выполните умножение трехзначного числа на однозначное:
327 · 3 = 432 · 4 = 151 · 7 =
3. Вспомните правило умножения суммы на число, правило умножения разности на число:
при умножении суммы (а + b) на число c, нужно каждое слагаемое умножить на это число и сложить полученные произведения:
(а + b) · с = a · c + b · c
При умножении разности (а − b) на число с, нужно уменьшаемое и вычитаемое умножить на это число и из первого произведения вычесть второе:
(а – b) · с = a · c – b · c
Сравните не вычисляя:
(72 + 12) · 5 * 72 · 5 + 12 · 5 (41 – 17) · 9 * 76 · 9 – 17 · 9
(68 – 45) · 4 * 68 · 4 – 21 · 4 (35 + 23) · 8 * 35 · 7 + 23 · 7
(29 + 83) · 3 * 29 · 3 + 83 · 2 (94 – 36) · 7 * 94 · 7 – 36 · 7
4. Решите задачу разными способами и укажите, какое правило является обобщением этих способов решения:
На автопарковке имеется 10 рядов по 30 машин, и 10 рядов по 40 машин. Сколько всего машин может вместить автопарковка?
Образец.
Студенты посадили 5 рядов по 10 яблонь, и 5 рядов по 15 груш. Сколько всего деревьев посадили студенты?
Решение:
1способ
10 ∙ 5 + 15 ∙ 5 = 125 (д) – всего посадили студенты
2 способ
(10 + 15) ∙ 5 = 125 (д) – всего посадили студенты
Равенство (10 + 15) ∙ 5 = 10 ∙ 5 + 15 ∙ 5 выражает распределительное свойство умножения относительно сложения.
2.2.2 Аналогия при формировании умений решать задачи.
Аналогия при формировании понятия задача.
Задача – это проблемная ситуация с явно заданной целью, которую необходимо достичь [20, с. 115]. Задачи, рассматриваемые в начальной школе, называют арифметическими, сюжетными, текстовыми. Текстовая задача – описание на естественном языке некоторого явления (ситуации, процесса) с требованием дать количественную характеристику какого-либо компонента этого явления, установить наличие или отсутствие некоторого отношения между компонентами или определить вид этого отношения [21, с. 58]. В структуру «задача» входят два основных элемента: условие и вопрос.
Условие формулируется в виде утверждения и представляет собой количественную и качественную характеристику объектов задачи и отношений между ними. В задаче обычно не одно, а несколько условий. Кроме того, условия содержат слова разной значимости: ключевые слова, а также предназначенные для «украшения» текста (создают его занимательность, оригинальность), для связки других слов. Нужно научить различать эти виды слов в условии, понимать их назначение. Главным же является процесс нахождения и использования ключевых слов, так как именно они позволяют ограничивать теорию и выделять только необходимую её часть. С этими словами нужно быть особенно «аккуратными», понимать их смысловое значение, ни в коем случае не терять, иначе задача делается нерешаемой.
Задача
| Условие задачи | У Маши 3 тетради, у Вити 2. |
| Вопрос задачи | Сколько всего тетрадей у Маши и у Вити? |
| Решение задачи | 3 + 2 = 5 |
| Ответ задачи | 5 тетрадей |
Например: У Маши 3 тетради, Вити – 2. Сколько всего тетрадей у Маши и Вити?
Слова «Маша», «Витя» не являются ключевыми (неважно, кто, их можно заменить любыми другими, они никакого влияния не оказывают).
Слова «тетради» – очень важные, так как они содержат информацию. Упустив эти слова, мы не сможем решить задачу. Это объекты задачи.
«У Маши 3 тетради» – ключевые слова, указывающие на количество тетрадей у девочки.
«у Вити - 2» – ключевые слова, указывающие на количество тетрадей у мальчика. Теперь надо сопоставить вопрос задачи с условием и найти ответ.
Вопрос (требование) задачи состоит из вопросительного слова и объекта поиска (иногда в вопросе можно обнаружить часть условия). Каждое вопросительное слово имеет своё значение и задаёт направление поиска. Например, «куда?» – указывает на время, «где?» – на место, «сколько?» – на количество, «почему?» – на причину.
Если ученики отвечают на вопросы «невпопад» – это значит, что они не понимают значения вопросительных слов, и необходимо спланировать работу по освоению их значения. Объект в вопросе указывает на теоретическое основание или вывод на теорию.
Вопрос нашей задачи «Сколько всего тетрадей у Маши и Вити?» выводит на теоретическое понятие «количество».
В учебниках математики для начальной школы формирование понятия «задача» происходит так. Детям предлагается прочитать два текста и затем ответить на вопросы.
| Мальчик поставил на первую полку 23 книги, а на вторую 7. Всего он поставил 30 книг на две полки. | Мальчик поставил на первую полку 23 книги, а на вторую 7. Сколько всего книг он поставил на полки? |
- Сравни тексты. Чем эти тексты похожи? Чем отличаются?
- Какой текст вы считаете задачей? Почему?
- Какое действие поможет ответить на вопрос задания?
- Что тебе подсказало действие для решения задачи?
- Ты знаешь, каким действием нужно решить эту задачу?
- Раздели задачу на 2 части.
- Сделай к задаче рисунок и реши её.
- Придумай и запиши другую задачу к тому же рисунку.
- Найди и прочитай ту часть задачи, которая рассказывает, что в ней известно.
- Прочти вторую часть задачи, о чём она тебе сообщила?
- Прочитай текст и докажи что это задача.
- Назови данные числа. В какой части задачи ты их отыскал?
Очень полезно показывать учащимся, как создаются задачи, так как этот процесс способствует осознанному представлению о структуре задачи, а также развитию математических способностей и мышления младших школьников.
Аналогия при формировании умения решать задачи.
В методике обучения решать задачи определяют два принципиально различных подхода.
1 подход:
Цель: формировать умение решать задачи определенных видов (типов).
2 подход:
Цель: научить выполнять семантический и математический анализ текста задач. Выявлять взаимосвязь между условием и вопросом. Представлять эти связи в виде схематических и символических моделей.
Различные цели определяют и методику обучения решению задач.
При 1 подходе, сначала учим решать простые задачи, а затем составные, состоящие из изученных простых.
-
I – 5 кн.
II – 3 кн.
-
I – 5 кн.
II – ?, на 2 кн. м.
-
I – 5 кн.
II – ?, на 2 кн. м.
При этом, простые задачи решаются на предметном уровне, а затем учитель знакомит учащихся с образцом записи решения задачи.
Например: на первой полке было 6 книг, а на второй 3. Сколько всего книг на двух полках вместе?
Запись можно представить следующим образом:
I – 5 кн.
II – 3 кн.
В методике обучения решению задач каждого вида, как простых, так и составных, выделяют 3 этапа:
1 подготовительный.
2 ознакомление с задачами данного типа.
3 формирование умения решать задачи данного вида.
При втором подходе, обучение решению задач состоит в том, что мы пытаемся сформировать у учащихся самостоятельную учебную деятельность, в плане решения задач. исходя из жизненных реалий мы понимаем, что невозможно обучиться этому с одинаковым уровнем успешности в одинаковые сроки. Однако попытаться сформировать у учащихся умение самостоятельно работать над задачей, это одна из методических линий современной методики обучения математики в начальной школе.
Решение задач, как правило, связано с построением умозаключений.
| Цена | Количество | Стоимость |
| 15 р | 3 шт | ? |
| ? | 3шт | 45р |
| 15р | ? | 45р |
С = Ц*К
Рассуждение учащихся будет следующим:
Чтобы найти стоимость, надо цену умножить на количество (это общая посылка). В задаче известна цена 15 рублей и количество 3 штуки (это частная посылка). Значит можно найти стоимость 15 * 3 = 45 (р) (это заключение).
Затем опираясь на формулу С = Ц*К и известное в задаче, учащиеся по образцу находят общую и частную посылку, и приходят к заключению, т.е. Ц= С:К (45:3=15), К= С:Ц (45:15=3)
Следовательно, до решения задач надо сформулировать у учащихся такие логические умения как:
- анализ
-синтез
-сравнение
-аналогия
-и т.д.
До решения задач дети должны приобрести опыт в соотнесении предмета действий к символическим записям.
3 + 1 = 4
Методика работы с каждым видом задач ведется также в соответствии с 3 ступенями: подготовительная, ознакомительная, закрепление. А процесс решения задач осуществляется поэтапно:
-
Ознакомление с содержанием задачи.
-
Поиск решения задачи.
-
Составление плана решения задачи.
-
Запись решения и ответа.
-
Проверка решения задачи.
Рассмотреть процесс решения задач вы можете в приложении 1.
Работа, проведенная на этапе знакомства с текстовой задачей, позволяет организовать деятельность учащихся направленную на усвоение ее структуры и на осознание процесса ее решения.
Н. Б. Истомина выделяет несколько методических приемов обучения решению задач.
- выбор схемы.
- выбор вопросов.
- выбор выражений.
- выбор условий к данному вопросу.
- выбор данных.
-изменение текстов задачи в соответствии с данным решением.
- постановка вопросов, в соответствии данных схем.
- объяснение выражений, составленных по данному условию.
- выбор решения задачи.
Рассмотреть некоторые из приемов вы можете в приложении 2:
Для организации продуктивной деятельности учащихся, направленной на формирование умения решать текстовые задачи, учитель может использовать обучающие задания, включающие различные сочетания методических приемов.
Более распространенные задачи, включающие различные сочетания методических приемов, в частности приема аналогии, являются виды задач на нахождение пропорциональных величин, например:
1. На нахождение массы:
a) В саду собрали 4 корзины малины. Сколько кг малины собрали в саду, если в одну корзину помещается 6 кг малины?
b) Всего в саду собрали 24 кг малины. Сколько корзин собрали, если в одну корзину помещается 6 кг малины?
c) Всего в саду собрали 4 корзины малины. Сколько кг малины помещается в одну корзину, если собрали 24 кг малины?
| Масса 1 корзины | Количество корзин | Общая масса | Решение |
| 6 кг | 4 к | ? | 6 * 4 = 24 (кг) |
| 6 кг | ? | 24 кг | 24 : 6 = 4 (к) |
| ? | 4 к | 24 кг | -
4 = 6 (кг) |
2. На нахождение ЦКС.
-
За 2 стакана чаю заплатили 8 рублей. Сколько стоит один такой стакан?
-
Один стакан чаю стоит 4 рубля. Сколько стаканов чая купили, если за чай заплатили 8 рублей?
-
Один стакан чая стоит 4 рубля. Сколько рублей заплатили за 2 стакана чая?
| Цена | Количество | Стоимость | Решение |
| 4 р. | 2 ст. | ? | 4 * 2 = 8 (р) |
| 4 р. | ? | 8 р. | 8 : 2 = 4 (р) |
| ? | 2 ст. | 8 р. | -
: 4 = 2 (р) |
-
На скорость, время, расстояние.
-
За час автомобиль проехал 40 км. Какое расстояние прошел автомобиль, если он был в пути 3 часа?
-
За 3 часа автомобиль прошел 120 км, какое расстояние прошел автомобиль за час?
-
За час автомобиль прошел 40 км. Сколько часов был автомобиль в пути, если он прошел расстояние 120 км?
| V | t | S | Решение |
| 40 км/ч | 3 ч | ? | 40 * 3 = 120 (км) |
| ? | 3 ч | 120 км | 120 : 3 = 40 (км/ч) |
| 40 км/ч | ? | 120 км | -
40 = 3 (ч) |
-
На нахождение работа/время/производительность
-
Оля за час лепит 30 пельменей. Сколько пельменей слепит Оля за 3 часа?
-
За 3 часа Оля слепила 90 пельменей. Сколько пельменей лепит Оля за час?
-
За час Оля лепит 30 пельменей. За сколько часов Оля слепит 90 пельменей?
| V | t | A | Решение |
| 30 п/ч | 3 ч | ? | 30 * 3 = 90 (п) |
| ? | 3 ч | 90 п | 90 : 3 = 30 (п/ч) |
| 30 п/ч | ? | 90 п | 90 : 30 = 3 (ч) |
Решение этих задач, способствует формированию умения решать задачи, развивает логическое мышление, расширяется представления учащихся о реальной действительности.
Формирование умения решать задачу занимает большое место в системе обучения младших школьников, так как:
1) задачи позволяют осознать реальные количественные отношения между различными объектами. Значит, через задачи расширяются представления учащихся о реальной действительности.
2) решение задачи помогает ученику осознать практическую значимость тех понятий, которые они изучают на уроке математики.
3) решение задач развивает мыслительную деятельность школьника, т.к. решение задач связано с выполнением анализа, синтеза, моделирования.
4) задачи способствуют формированию личностных качеств как: усидчивость, трудолюбие и т.д.
2.3. Аналогия при изучении математических понятий
Одной из характерных черт математики является ее связь с другими изучаемыми предметами, с жизнью. Задачи с межпредметным содержанием или прикладного характера помогают лучше раскрыть каждую тему, способствуют непроизвольному запоминанию, развивают интерес учащихся не только к предметам, но и самому процессу познания, повышают качество их знаний и умение их добывать. Связь математики с русским языком и литературой, с иностранным языком, историей и географией естественна. Математические термины точны и выразительны, наиболее близко передают смысл сказанного. Значение этих терминов чаще всего связано с их возникновением. Поэтому при изучении математических терминов целесообразно рассматривать их происхождение, а также значение в других областях человеческой деятельности. Это позволит повысить интерес к происхождению математических понятий, следовательно, и к математике, и к другим предметам, показать связь их с жизнью, с другими предметами.
Ниже представлены примеры некоторых понятий, изучаемых в начальном курсе математики, дополнительные сведения о которых можно использовать на уроках в начальной школе (таблица 1).
Таблица 1
| Значение понятия в математике | Значение понятия в других областях | Перевод с греческого, латинского |
| Квадрат – 1) прямоугольник с равными сторонами. 2) вторая степень числа (а), то есть а2 | Квадрат – в полиграфии единица длины, применяемая для измерения шрифтов, формата набора. 1 квадрат = 48 пунктам (ок. 18,05 мм). | От лат. – quadratus − четырехугольный |
| Круг - часть плоскости, ограниченная окружностью (содержащая ее центр). Площадь круга S =  R R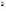 , где R - радиус окружности, а = 3,141592654… - отношение длины окружности к диаметру. , где R - радиус окружности, а = 3,141592654… - отношение длины окружности к диаметру. | Круг – в древности, повязка на плече как знак отличия | От лат. «кольцо» |
| Линия - общая часть двух смежных областей поверхности. Движущаяся точка описывает при своем движении некоторую линию. Прямая линия – черта или прямая | Линия - 1) единица длины в системе английских мер, 1 линия = 1/12 дюйма =0,21167 см. 2) В России - мера длины, 1 линия = 10 точкам =2,54 мм. | от лат. linea – льняная нить |
| Периметр - длина замкнутого контура, сумма длин всех сторон многоугольника | Периметр - в математике: граница плоской фигуры, а также длина этой границы. | от греч . perimetreo - измеряю вокруг греч. perimetron - окружность |
| Ромб – параллелограмм с равными сторонами | Ромб - Название высшего офицерского знака различия такой формы на петлицах в Красной Армии | греч . rhombos |
| Треугольник - геометрическая фигура - многоугольник с тремя углами. Часть плоскости, ограниченная тремя отрезками прямых (сторонами треугольника), имеющими попарно по одному общему концу | Треугольник - Созвездие Северного полушария; с территории России лучше всего видно в конце лета, осенью и зимой. | лат . Triangulum |
| Угол (плоский) - геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла). | Угол – перелом, излом, колено, локоть, выступ или залом (впадина) об одной грани. Часть плоскости между двумя прямыми линиями, исходящими из одной точки | Ср. лат. angulus – “угол” |
| Шар - геометрическое тело, получающееся при вращении круга вокруг своего диаметра. Шар - часть пространства, ограниченная сферой. | Шар - у землекопов, слой, пласт земли. Класть масло шарами, в переслойку Шар - стар. церк., краска. | слой, пласт или ряд (польск. szar, ряд, гонта, черепицы) лат. sphaera шар, от греч. – мяч |
| Сумма – 1. Итог, результат сложения. 2. Общее количество чего-нибудь (сумма всех данных). 3. Определённое, то или иное количество денег (затрачены крупные суммы)
| Сумма - итог, общее количество. Например: «К сумме разнородных впечатлений неожиданно прибавилось ещё одно новое» (Лесков); «Сумма всех данных»; «Вся сумма человеческих знаний». | лат. summa – “итог”, “общее количество” |
| Площадь – 1. В математике: часть плоскости, заключённой внутри замкнутой геометрической фигуры (площади квадрата). 2. Незастроенное большое ровное место (в городе, в селе), от которого обычно расходятся в разные стороны улицы (Красная площадь в Москве). 3. Пространство. Помещение, предназначенное для какой-нибудь цели (полезная площадь в доме). | Площадь - часть поверхности, ограниченная каким-либо замкнутым контуром. Величина П. выражается числом заключающихся в ней квадратных единиц. | греч. plateia – “широкая”. |
|
| Цифра - индийские математики называли знак обозначавший отсутствие некоторого разряда словом “сунья” - пустой. | лат. cifra – “цифра”, происходящего от арабск.слова “сифр”, означающего “нуль”. |
| ОВАЛ - замкнутая выпуклая плоская кривая. При этом под выпуклостью понимают свойство кривой иметь с любой прямой не более двух (действительных) общих точек. | Овал - овал лица определяется соотношением ширины лба к ширине подбородка, а также пропорцией длины и ширины лица. | от лат. ovum - яйцо |
Кроме того, для того, чтобы детям было интереснее изучать предмет, им можно предложить изучение материала в различном виде. Несколько вариантов заданий вы можете посмотреть в приложении 3.
Также при изучении математических терминов, мы показываем учащимся, что есть понятия, в которых одно понятие вытекает из другого изученного ранее.
Возьмем, к примеру, понятия: «Треугольник» и «Прямоугольник». Учащимся дается следующее задание.
Сравни фигуры.
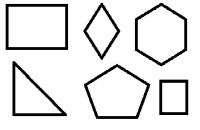
-В чем их сходство?
-В чем различие?
Эти фигуры называются многоугольниками.
Многоугольник – это плоская геометрическая фигура, состоящая из отрезков, пересекающихся в трех или более точках.
Подумай, почему этой группе фигур дали такое название.
Посмотри на рисунок 2. Попробуй делением фигур на две группы, дать определение треугольника.
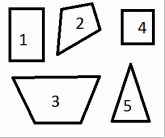
-Сравни свое определение с таким:
Треугольник - геометрическая фигура - многоугольник с тремя углами.
-Определения похожи? Если не похожи, то чем?
-Найди в окружающем пространстве предметы, имеющие форму треугольника.
Таким образом, прием аналогии можно использовать при изучении различных математических понятий, законов, формировании общеучебных умений.
Заключение.
В процессе исследования в соответствии с поставленной целью и задачами получены следующие основные выводы и результаты:
1. На основе проведённого анализа математической и логической литературы обоснована необходимость применения основных видов умозаключений – дедуктивные, индуктивные и по аналогии. При этом отмечено, что индуктивные умозаключения и умозаключения по аналогии носят недостоверный, а гипотетический характер, потому требуют доказательства.
2. Аналогия в начальном курсе математики занимает большое место. Обнаружение сходства или различия между предметами поднимает наше мышление на более высокую степень. Учащийся учится умению делать предположения, умению познавать неизвестное, овладевает навыками логического исследования предметов и явлений окружающей действительности.
3. Проведён анализ учебников математики по программе «Перспектива». Анализ учебников позволяет сделать вывод, что прием рассуждений по аналогии достаточно широко используется в той и другой образовательной системе.
4. Разработано методическое пособие по использованию приема аналогии при обучении математике в начальных классах. Оно представляет собой набор дидактических материалов для использования аналогии при изучении законов арифметических действий, при формировании понятия «задача», при изучении различных математических понятий.
В заключении хочу отметить, что обращение к аналогии может диктоваться различными задачами. Она может привлекаться для получения нового знания, для того, чтобы менее понятное сделать более понятным, представить абстрактное в более доступной форме, конкретизировать отвлеченные идеи, проблемы и т.д. по аналогии также можно рассуждать о том, что недоступно прямому наблюдению. Аналогия может служить средством выдвижения новых гипотез, являться своеобразным методом решения задач путем сведения их к ранее изученным задачам и т.п.
Список использованных источников
-
Алексеева, Л. Л. Планируемые результаты начального общего образования / Л. Л. Алексеева, С. В. Анащенкова, М. З. Биболетова. – М.: Просвещение, 2009. – 120 с.
-
Асмолов, А. Г. Как проектировать универсальные учебные действия в начальной школе / А. Г. Асмолов, Г. В. Бурменская, И. А. Володарская. – М.: Просвещение, 2008. – 151 с.
-
Горский Д. П. Краткий словарь по логике / Д. П. Горский, А. А. Ивин, А. Л. Никифоров; Под ред. Д. П. Горского. – М.: Просвещение, 2008. – 208 с.
-
Дорофеев, Г. В. Математика. 4 кл.: учеб.: В 2 ч. Ч 1: учебник / Г. В. Дорофеев., Т. Н. Миракова, Т. Б. Бука. – М.: Просвещение, 2015. – 128 с.
-
Дорофеев, Г. В. Математика. 4 кл.: учеб.: В 2 ч. Ч 2: учебник / Г. В. Дорофеев., Т. Н. Миракова, Т. Б. Бука. – М.: Просвещение, 2015. – 128 с.
-
Дорофеев, Г. В. Математика. 3 кл.: учеб.: В 2 ч. Ч 1: учебник / Г. В. Дорофеев., Т. Н. Миракова, Т. Б. Бука. – М.: Просвещение, 2014. – 128 с.
-
Дорофеев, Г. В. Математика. 3 кл.: учеб.: В 2 ч. Ч 2: учебник / Г. В. Дорофеев., Т. Н. Миракова, Т. Б. Бука. – М.: Просвещение, 2014. – 128 с.
-
Дорофеев, Г. В. Математика. 2 кл.: учеб.: В 2 ч. Ч 1: учебник / Г. В. Дорофеев., Т. Н. Миракова, Т. Б. Бука. – М.: Просвещение, 2015. – 122 с.
-
Дорофеев, Г. В. Математика. 2 кл.: учеб.: В 2 ч. Ч 2: учебник / Г. В. Дорофеев., Т. Н. Миракова, Т. Б. Бука. – М.: Просвещение, 2015. – 122 с.
-
Дорофеев, Г. В. Математика. 1 кл.: учеб.: В 2 ч. Ч 1: учебник / Г. В. Дорофеев., Т. Н. Миракова, Т. Б. Бука. – М.: Просвещение, 2011. – 128 с.
-
Дорофеев, Г. В. Математика. 1 кл.: учеб.: В 2 ч. Ч 2: учебник / Г. В. Дорофеев., Т. Н. Миракова, Т. Б. Бука. – М.: Просвещение, 2011. – 128 с.
-
Иванова, Е. В. Развитие логического мышления младших школьников на уроках математики / Е. В. Иванова // Начальная школа плюс до и после. – 2006. – №6. – С. 59-60.
-
Ивлев, Ю. В. Логика : учеб. − 3-е изд., перераб. и доп. / Ю. В. Ивлев – М. : ТК Велби, изд. Проспект, 2006 – 348 с.
-
Истомина, Н. Б. Активизация учащихся на уроках математики в начальных классах: пособие для учителя − 5-е изд., перераб. / Н. Б. Истомина. – М. : Просвещение, 2007. – 63 с.
-
Истомина, Н. Б. Методика обучения математики в начальных классах: учеб. − 3-е изд., перераб / Н. Б. Истомина. – М. : Ц. «Академия», 2007. – 234 с.
-
Копкин, П. В. О некоторых вопросах теории умозаключений // Вопросы логики. – М. : Изд-во Академия Наук СССР, 1999. – 328 с.
-
Кутасов, А. Д. Элементы математической логики / А. Д. Кутасов – М. : Просвещение, 2008. – 63 с.
-
Столяр, А. А. Логические проблемы преподавания математики / А. А. Столяр. – Минск : «Высш. школа», 2009. – 254 с.
-
Стойлова, Л. П. Математика : учеб-к для студ. высш. пед. учеб. заведений / Л. П. Стойлова. − М. : Академия, 2007. − 432 с.
-
Стойлова, Л. П. Математика / Л. П. Стойлова. – М. : Издательский центр «Академия», 2007. – 318 с.
-
Тихомиров, О. К. Психология мышления / О. К. Тихомиров. – М. : Академия, 2008. – 288 с.
-
Хинчин, А. Я. Педагогические статьи. Вопросы преподавания математики. Борьба с методическими штампами / А. Я. Хинчин. – М. : КомКнига, 2006. – 208 с.
-
Хомякова, Л. В. Индуктивные рассуждения в курсе математики в начальных классов / Л. В. Хомякова // Начальная школа. – 2003. – №5. – С. 31-36.
-
Шикалиев, Х. Ш. О некоторых приёмах развития доказательных рассуждений учащихся начальных классов / Х. Ш. Шикалиев, Б. О. Омаров // Начальная школа. – 2007. – № 6. – С. 98-101.
-
Шмырева, Г. Г. Из опыта работы по учебникам математики Н. Б. Истоминой / Г. Г. Шмырева, С. М. Нестерович // Начальная школа. – 2007. – № 8. – С. 46-49.
Приложение.
Приложение 1
Рассмотрим процесс решения задач, на примере конкретной задачи:
В одном бидоне 7 литров подсолнечного масла, а в другом на 4 литра меньше. Сколько литров подсолнечного масла в двух бидонах вместе?
I этап: анализ текста.
1. Прочитайте задачу.
2. О чем говорится в задаче?
3. Что мы знаем о первом бидоне?
4. Что мы знаем о втором бидоне?
5. Как вы понимаете на 4 литра меньше?
6. Что нам требуется найти?
Вспомогательную модель выполняют одновременно с анализом текста.

7. Можем ли мы сразу ответить на вопрос задачи?
II этап: поиск решения (от условия).
1. Зная что в 1 бидоне 7 литров, а во втором на 4 меньше. Что мы можем узнать? Каким действием? Почему вычитанием?
2. Узнав сколько литров во втором бидоне и зная, сколько литров масла в первом. Можем ли мы ответить на вопрос задачи? Каким действием? Почему сложением?
III этап: оформление решения.
Записываем решения по действиям с кратким пояснением.
1. 7 – 4 = 3 (л) – масла во II бидоне.
2. 7 + 3 = 10 (л) – масла вместе в двух бидонах.
IV этап: формулирование и запись ответа.
Сначала ответ формулируется устно, затем записывается в тетрадь.
Ответ: 10 литров подсолнечного масла было в двух бидонах вместе.
Приложение 2.
1) Выбор выражений.
На велогонках стартовало 70 спортсменов. На первом этапе с трассы сошли 44 велосипедиста, на втором – 6. Сколько спортсменов пришло к финишу?
Выбери выражение, которое является решением задачи:
6 + 4 6 – 4 70 – 6
70 – 6 – 4 70 – 4 – 6 70 – 4
2) Объяснение выражений, составленных по данному условию.
Фермер отправил в магазин 45 кг укропа, петрушки на 4 кг больше, чем укропа, и 19 кг сельдерея. Сколько всего килограммов зелени отправил фермер в магазин?
Что обозначают выражения, составленные по условию задачи?
45 – 19 45 + 19 45 + 4 45 – 4
3) Выбор решения задачи.
Курица легче зайца на 4 кг, а заяц легче собаки на 8 кг. На сколько, собака тяжелее курицы? На сколько, курица легче собаки?
Маша решила задачу так: 8 + 4 = 12 (кг)
Миша решил задачу так: 8 – 4 = 4 (кг)
Посмотрите на схему. Кто прав: Миша или Маша?
4) выбор условий к данному вопросу.
Подбери условия к данному вопросу и реши задачу.
Сколько всего детей занимается в студии?
А) в студии 30 детей из них 15 мальчиков.
Б) в студии 8 мальчиков, а девочек на больше меньше.
В) в студии мальчики и девочки. Мальчиков на 7 меньше чем девочек.
Г) в студии 8 мальчиков и 20 девочек.
Приложение 3.
Варианты заданий изучения математических понятий.
А) Подготавливаются карточки двух видов. На одних карточках написаны математические термины. Например: овал, круг, цилиндр, угол, шар, куб, площадь.
На других – перевод этих слов с латинского или греческого языков с изображением соответствующего объекта. Например:






На обратной стороне этих карточек можно написать историю происхождения и развития этих терминов, интересные сведения из опыта их использования. Это позволит повысить интерес, расширить кругозор детей, повысить мотивацию учения.
Б) также можно подготовить карточки, следующих видов. При подведение к новому термину. Например: отрезок, дробь, угол.



Такой подход разнообразит урок, в котором происходит изучение математических терминов. А также повысит интерес учащихся и мотивацию к изучению нового термина.
35













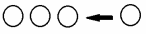
 R
R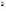 , где R - радиус окружности, а = 3,141592654… - отношение длины окружности к диаметру.
, где R - радиус окружности, а = 3,141592654… - отношение длины окружности к диаметру.

































