
Формирование вычислительных навыков на уроках математики
Из опыта работы Черёмушкиной Ирины Викторовны

План. 1. Роль устных упражнений на уроках математики. 2. Некоторые особенности дидактического момента – устная работа. 3. Условия эффективности устных упражнений. 4. Устные упражнения, как подготовительные для изучения нового материала. 5. Устный счет и его виды. 6. Упражнения на готовых чертежах на уроках геометрии. 7. Дидактические игры – как один из методов устной работы на уроках математики. 8. Практические рекомендации для проведения устной работы. 9. Литература.

1.Роль устных упражнений на уроках математики.
Правильно организованные упражнения учащихся в решении задач – важное средство активизации мыслительной деятельности учащихся и развитие их творческих способностей.
Особое внимание заслуживают устные упражнения. Они эффективны кажущейся легкостью, эмоциональностью, действуют на учащихся мобилизующе, своей простотой увлекают и слабых школьников, создают в классе обстановку соревновательности. Устные упражнения способствуют развитию внимания и памяти учащихся.

1.Роль устных упражнений на уроках математики.
Одним из средств, способствующих лучшему усвоению математики, являются устные упражнения. С их помощью учащиеся отчетливее понимают сущность математических понятий, теорем, математических преобразований.
Устная работа на уроках математики весьма оживляет урок. На ней можно отдохнуть; в хорошем смысле этого слова, развлечься. Это самый «свободный» этап урока. Вопросы быстро сменяют друг друга, и если не знаешь ответ на один, то не беда, сможешь проявить себя на следующем. Это очень динамичный, активный вид деятельности, вносящий разнообразие в уроки математики. Кроме того, каждый ученик может отличиться «заработать» поощрение, хорошую оценку и т.п.

1.Роль устных упражнений на уроках математики.
Устные упражнения активизируют мыслительную деятельность учащихся, развивают внимание, наблюдательность, память, речь, быстроту реакции, повышают интерес к изучаемому материалу. Они дают возможность изучить большой по объему материал за более короткий промежуток времени, позволяют учителю судить о готовности класса к изучению нового материала, о степени его усвоения, помогают выявлять ошибки учащихся.

1.Роль устных упражнений на уроках математики.
Проводимые в начале урока устные упражнения помогают учащимся быстро включаться в работу, в середине или конце урока служат своеобразной разрядкой после напряжения и усталости, вызванных письменной или практической работой. В ходе выполнения этих упражнений учащиеся чаще, чем на других этапах урока, получают возможность устно отвечать, причем они сразу проверяют правильность своего ответа. В отличие от письменных упражнений содержание устных таково, что решение их не требует большого числа рассуждений, преобразований, громоздких вычислений.

2.Условия эффективности устных упражнений.
Но далеко не всегда устные упражнения приводят к ожидаемым результатам. Причина этого в том, что методика проведения устных упражнений сложнее, чем письменных. Когда класс записывает решение задачи, учитель видит, кто работает и как работает, видит в тетрадях также и результаты работы. А как проверить, действительно ли все учащиеся активно думают над задачей при ее устном решении? Отвечает – то всегда один ученик и сообщает он, как правило, только результат выполненного упражнения, а процесс его получения остается скрытым.

Содержание
Цели
Форма организации
Дидактический момент
Результат

Выделим некоторые особенности дидактического момента – устная работа. Ее основными дидактическими функциями являются такие:
Улучшение усвоения математики, более сознательное неформальное усвоение предмета.
Подготовка учащихся к работе на уроке, в частности к восприятию нового материала.
Систематическое повторение пройденного.
Форма проверки знаний, умений и навыков учащихся.
Формирование интереса к предмету.
Развитие учащихся (внимания, памяти, наблюдательности, сообразительности, инициативы и т.п.).
Активизация учебной деятельности на уроке.

В содержание устной работы, по - возможности, нужно включать упражнения следующих типов:
на закрепление и отработку текущего материала;
на закрепление и отработку текущего материала;
на повторение
на повторение
с элементами творчества (например, для подготовки к восприятию нового материала, с новой для ребят пространственной ситуацией и т.д.);
с элементами творчества (например, для подготовки к восприятию нового материала, с новой для ребят пространственной ситуацией и т.д.);
развивающего характера (в том числе нестандартные упражнения, на сообразительность, занимательные).
развивающего характера (в том числе нестандартные упражнения, на сообразительность, занимательные).

3.Условия эффективности устных упражнений.
Проводя устные упражнения, учитель должен быть уверен, что работают все, и притом активно. Он должен также получить обратную информацию: как выполнили упражнение, усвоен ли способ решения. Отсюда вывод: чтобы гарантировать участие в работе всех учащихся, нужно, очевидно, соблюдать ряд условий эффективности устных упражнений.

Задачи для устных упражнений в 5-11 классах быть заранее выписаны на отдельных листах или на доске
Устные упражнения желательно чередовать с письменным выполнением упражнений аналогичного типа на самостоятельных и контрольных работах.
Условия геометрических задач, решаемых устно, желательно задавать хотя бы частично на чертеже.
Во время устных упражнений следует особенно тщательно соблюдать паузы, чтобы учащиеся успевали обдумать решения задач.
На уроках алгебры задачи нового типа сначала лучше решать письменно и лишь затем для закрепления навыков – устно. В таком случае учащиеся через некоторое время свободно решают устно довольно сложные для них задачи
При устном решении задач особенно важно соблюдать принципы построения системы упражнений (однотипности, непрерывного повторения, использования
Условия задач для устного решения можно задавать на таблицах, плакатах, с помощью

4. Устные упражнения, как подготовительные для изучения нового материала.
Такие упражнения, проводимые в течение 5-7 минут в начале урока, мобилизуют всех ребят, они кажутся простыми и доступными для всех. Даже у самых слабых учеников появляется надежда на то, что и они могут делать что-то на уроке. Таким образом, достигается еще одна цель – работа на уроке всех ребят, при этом отступает боязнь, появляется уверенность в себе и вера в учителя.

ТРЕНАЖЕР ПО ТЕМЕ «ТЕОРЕМА ПИФАГОРА»
Е
1).
О
Е
М
4).
3).
2).
?
6 см
?
Д
12 см
?
?
12 см
8 см
К
Д
М
А
С
Р
Н
5 см
7 см
F
7).
6).
С
5).
В равнобедренном треугольнике АВМ основание АМ равно 18 см, а боковая сторона – 15 см.Найдите высоту, проведенную к основанию.
FE= EN
20 см
5 см
х
Н
N
х
Е
М
8). В прямоугольной трапеции АВСД с основаниями АВ и СД угол А – прямой. ВС=17см, АД= 8 см, АВ= 20 см.Найдите длину стороны СД .
Удачи!

Устный счет и его виды. Следует разделять два вида устного счета.
- Первый – это тот, при котором учитель не только называет числа, с которыми надо оперировать, но и демонстрирует их учащимся каким-то образом. Подкрепляя слуховые восприятия учащихся, зрительный ряд фактически делает ненужным удерживание данных в уме, чем существенно облегчает процесс вычислений.
- Второй вид устного счета - когда числа воспринимаются только на слух. Учащиеся при этом ничего не записывают и никакими наглядными пособиями не пользуются.

Математическая зарядка.
- Большое значение на каждом уроке имеет его организационный момент. Как быстро настроить детей на работу, но сделать это без понуканий и строгости? Можно провести оргмомент в виде математической зарядки.
- Заранее готовится несколько карточек с простейшими примерами. Примеры даются с ответами. На одних карточках ответы верные, на других – неверные. Каждое упражнение зарядки состоит их двух движений. Учитель поочередно показывает классу карточки, а ученики делают определенное движение. Например, если верный ответ – руки вверх, неверный – руки вперед. Сначала дети не могут собраться, не попадают в ритм. Но постепенно сосредотачиваются, а темп зарядки увеличивается. И в результате мы получаем класс, полностью подготовленный к работе.

Комплекс математической зарядки по теме «Делители и кратные»
1 упражнение .
Правильный ответ – руки вперед, неправильный ответ – руки вверх.
- 2*0,3=0,6
- 0,5*10=50
- 7*12=84
- 6:100=0,6
- 6 : 2=3
- 7+0,5=0,75
2 упражнение .
Все стоят, руки на поясе. Правильный ответ – поворот направо, неправильный – поворот налево.
- 2 – делитель 222
- 1 имеет один делитель
- 15 кратно 10
- любое число кратно 1.

«Молчанка». На доске изображаются фигуру. Вне каждой из них располагается четыре числа, а внутри записано действие, которое надо выполнить над каждым из «внешних» чисел. Ответы давать можно молча, написав рядом с данным числом верный результат указанного действия. Задания легко поменять, достаточно только заменить знаки арифметических действий, стоящие рядом с «внутренними» числами.
19,6
0,8
4.5
1,2
:2
9,7
*0,4
9,2
7,2
4,1
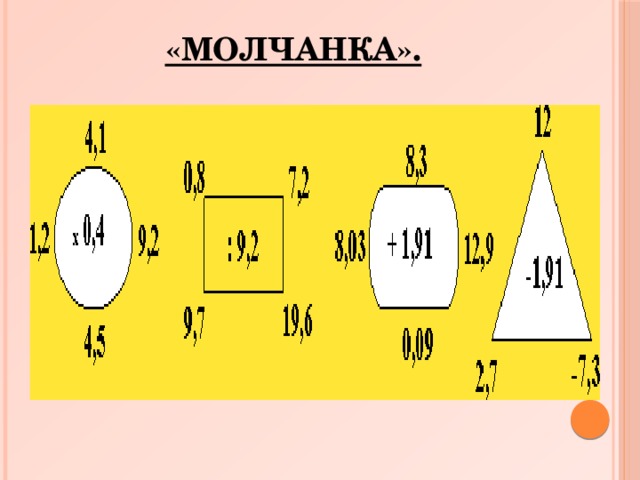
«Молчанка».
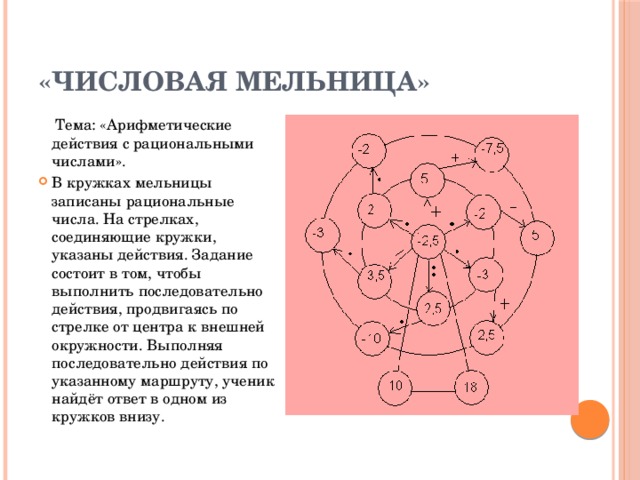
«Числовая мельница»
Тема: «Арифметические действия с рациональными числами».
- В кружках мельницы записаны рациональные числа. На стрелках, соединяющие кружки, указаны действия. Задание состоит в том, чтобы выполнить последовательно действия, продвигаясь по стрелке от центра к внешней окружности. Выполняя последовательно действия по указанному маршруту, ученик найдёт ответ в одном из кружков внизу.

«Мозаика геометрических фигур». Тема: « Площади многоугольников».
Вопросы учащимся:
- 1. Сколько всего равносторонних треугольников в мозаике?
- 2. Найти сумму периметров всех треугольников, если длину стороны меньшего из них принять за единицу.
- 3. Найти сумму площадей всех треугольников, если – «-.
Тема: «Длина окружности и площадь круга»
- Вопросы учащимся:
- 1. Сколько всего квадратов и кругов в мозаике?
- 20
- 2. Найти сумму периметров всех квадратов и сумму длин всех окружностей, если радиус меньшей окружности равен r.
- 3. Найти площади всех квадратов и кругов, если радиус большей окружности равен R.
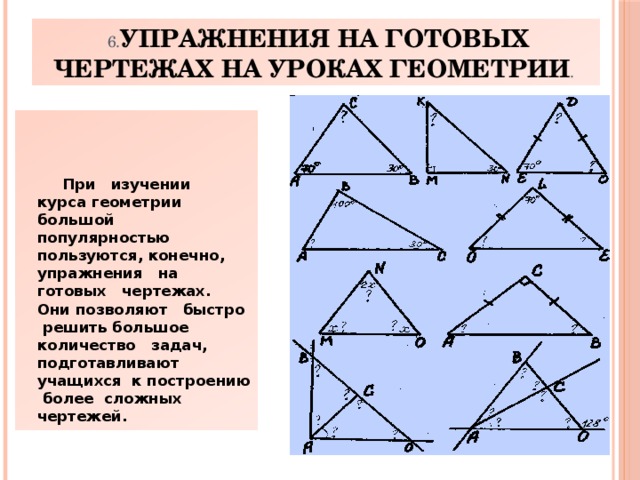
6. Упражнения на готовых чертежах на уроках геометрии .
При изучении курса геометрии большой популярностью пользуются, конечно, упражнения на готовых чертежах. Они позволяют быстро решить большое количество задач, подготавливают учащихся к построению более сложных чертежей.

Смежные и вертикальные углы
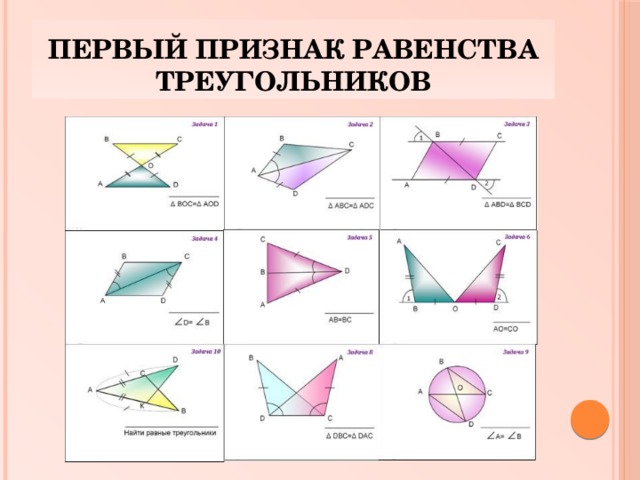
Первый признак равенства треугольников

Третий признак равенства треугольников


13 см
25см
реши задачи
12 cм
K
N
1.Дан прямоугольный треугольник KMN.
KN = 12cм, KM = 13см. Найти MN.
M
F
R
2.
Дан прямоугольник DFRO, RO:DO = 3:4
Найти FR, FD.
O
D
3. В треугольнике АВС высота CD, опущенная из вершины прямого угла С,
делит гипотенузу АВ на отрезки АD =9 см и DB = 16 см. Катет ВС = 20 см.
Найдите катет АС и высоту CD этого треугольника.

Найдите сумму векторов
Дано:
АВСD – параллелограмм
В
С
А
D
?
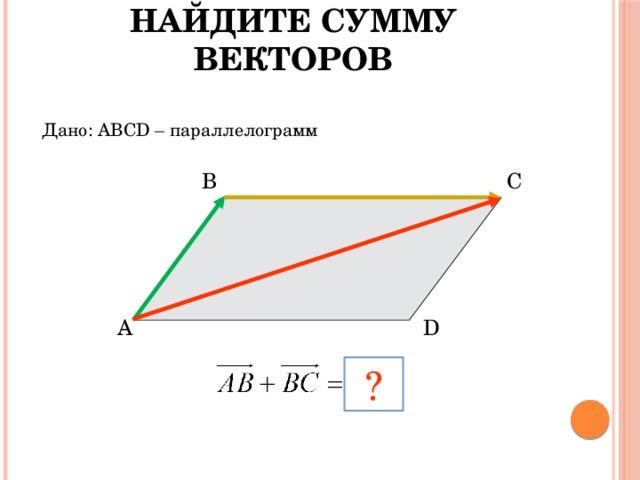
Найдите сумму векторов
Дано: АВСD – параллелограмм
В
С
А
D
?

Найдите сумму векторов
Дано: АВСD – треугольник
С
В
О
А
?
![На рисунке изображен график квадратичной функции y=f(x) на отрезке [-5; 2]. Найдите f(-8) 7 6 5 4 3 2 1 ПОДУМАЙ! 1 1 -7 -6 -5 -4 -3 -2 -1 ПОДУМАЙ! 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 2 Не существует ВЕРНО! Повтор 3 5 ПОДУМАЙ! 4 10 Маленький тест 18](https://fhd.multiurok.ru/f/5/1/f516192b9fd88ee1de8af101605a690bce350947/img_phpjNUW1S_formirovanie-vychislitelnyh-navykov-na-urokah-matematiki_0_30.jpg)
На рисунке изображен график квадратичной функции
y=f(x) на отрезке [-5; 2]. Найдите f(-8)
7
6
5
4
3
2
1
ПОДУМАЙ!
1
1
-7 -6 -5 -4 -3 -2 -1
ПОДУМАЙ!
1 2 3 4 5 6 7
-1
-2
-3
-4
-5
-6
-7
2
Не существует
ВЕРНО!
Повтор
3
5
ПОДУМАЙ!
4
10
Маленький тест
18
 0, D0 х a0, D0 a0, D a0, D у у a0, D0 a0, D=0 a0, D=0 a0, D 0 х 0 х a0 a a a" width="640"
0, D0 х a0, D0 a0, D a0, D у у a0, D0 a0, D=0 a0, D=0 a0, D 0 х 0 х a0 a a a" width="640"
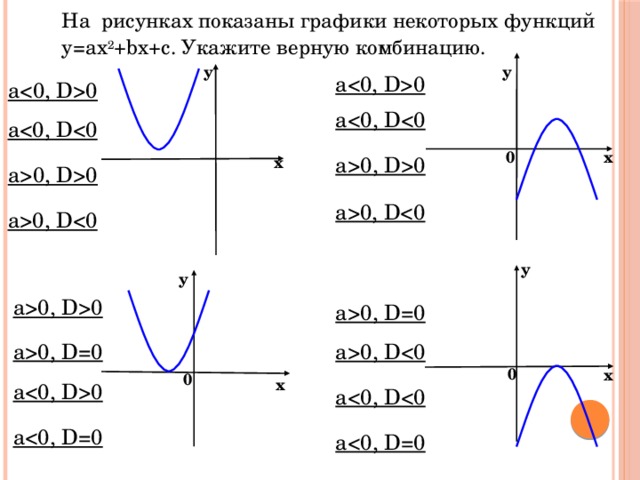
На рисунках показаны графики некоторых функций у=aх 2 +bx+с. Укажите верную комбинацию.
у
у
a0
а0
a
a
х
0
a0, D0
х
a0, D0
a0, D
a0, D
у
у
a0, D0
a0, D=0
a0, D=0
a0, D
0
х
0
х
a0
a
a
a
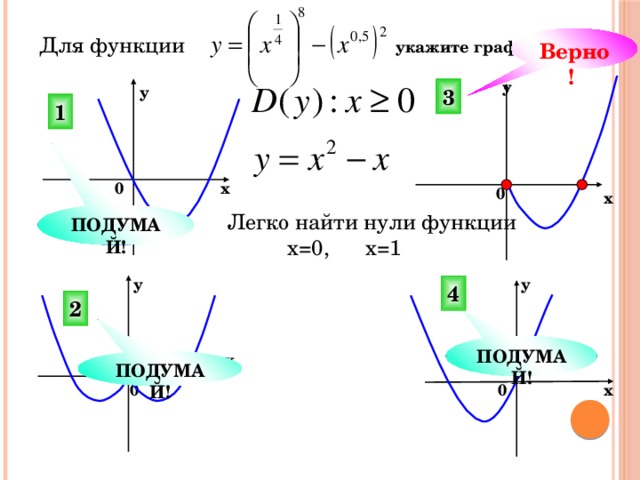
Для функции укажите график.
Верно!
у
у
3
1
х
0
0
х
ПОДУМАЙ!
Легко найти нули функции
х=0, х=1
у
у
4
2
ПОДУМАЙ!
х
ПОДУМАЙ!
0
0
х

Используя графические представления, подберите из
данных уравнений второе уравнение системы так,
чтобы она имела одно решение.
У
3
2
1
Два решения
у = х + 3
1
у = х 2
Два решения
-3 -2 -1
1 2 3 х
2
у = – х 2
-1
-2
-3
-4
ВЕРНО!
Повтор
3
у = х + 3
ТРИ решения
4
у = – х 3
Маленький тест
18

7.Дидактические игры
Изучению темы «Декартовы координаты на плоскости» может предшествовать игра в «Морской бой».
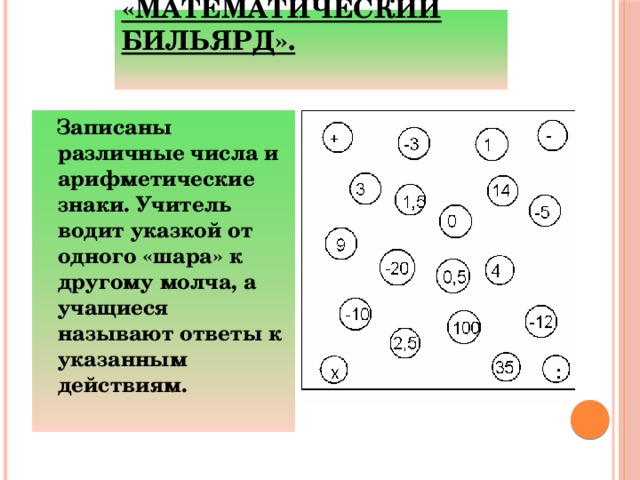
«Математический бильярд».
Записаны различные числа и арифметические знаки. Учитель водит указкой от одного «шара» к другому молча, а учащиеся называют ответы к указанным действиям.

«Лабиринт сомножителей». Тема: «Делимость натуральных чисел».
- В воротах лабиринта стоят делители числа 432. Поочередно члену каждой команды надо войти в лабиринт и дойти до центра, получив в произведении число 432. Движение можно выполнить и в обратном направлении. Побеждает та команда, у которой будет наибольшее число правильных ответов.

Кроссворд
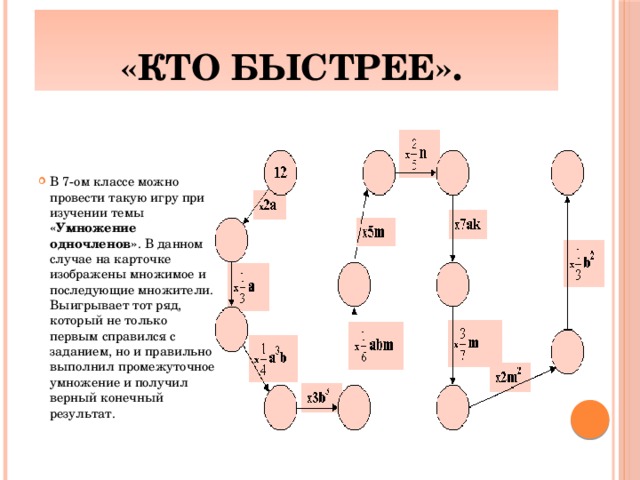
«Кто быстрее».
- В 7-ом классе можно провести такую игру при изучении темы «Умножение одночленов» . В данном случае на карточке изображены множимое и последующие множители. Выигрывает тот ряд, который не только первым справился с заданием, но и правильно выполнил промежуточное умножение и получил верный конечный результат.

«Кто быстрее».
- На каждый ряд раздают по одинаковой карточке, играющей роль эстафетной палочки, на которой написано по 5-6 примеров (по количеству парт в ряду). В первом примере требуется найти сумму двух чисел. Эта сумма подставляется во второй пример на место неизвестного слагаемого, только после этого можно получить ответ во втором примере.
- Результаты на карточках записываются простым карандашом и только после того, как тщательно проверено решение предыдущих примеров. Так как ошибочный результат в одном из промежуточных примеров приведет к неправильному итоговому результату.
6,2 + (-5) = …
… + (-4,6) = …
… + 10,9 = …
… + (-14) = …
… + 1,5 = …

«Беглый счет».
29,9 + 35,4 + 10,1 = ?
3,8 + 8,7 - 1,8 = ?
16,4 : 4
90,6 : 3
4,9 + 5,1 - 6,3 = ?
- Учащиеся устно выполняют действия и сообщают свои ответы. Карточки быстро сменяют друг друга, но последнее задание предлагается уже не с помощью карточек, а только устно.
- Две карточки могут
демонстрироваться одновременно.
- Выполнив действия, ребята должны сообщить на какой карточке ответ больше. Для такой работы полезно подбирать упражнения, в которых особенно заметен эффект прикидки.

8. Практические рекомендации для проведения устной работы
- На доске заранее написаны примеры в три столбика (по количеству рядов в классе). Соответственно ученики делятся на три команды. Первые участники игры от каждой команды одновременно подходят к доске, решают первые задания из своего столбика, затем возвращаются на свои места, отдав мел второму члену своей команды. Он также идет к доске, решает второй пример и передает эстафету дальше. Выигрывает та команда, которая быстро без ошибок выполнит свои задания. Такую эстафету лучше проводить в конце урока, когда учащиеся уже устали сидеть или если необходимо сменить обстановку.
«Эстафета».

Алгоритмы ускоренных вычислений
- Сложение с перестановкой слагаемых:
- Раздельное поразрядное вычитание :
72 + 63 + 28 = ?
574 – 243 = ?
Заметим, что третье слагаемое является дополнением первого до 100. Мысленно переставим слагаемые и сложим их:
Вычитаем из 500 число 200, получим 300. Вычитаем из 70 число 40, получаем 30. Вычитаем из 4 число 3, получаем 1. Ответ: 331.
72 + 28 + 63 = 163.
68 894 – 42 413 = ?
3013 + 74 + 2187 + 126 = ?
Вычитаем из 68 000 число 42 000, получаем 26 000. Вычитаем из 800 число 400, получаем 400. Вычитаем из 94 число 13, получаем 81. Ответ: 26 481.
Группируем слагаемые попарно:
(3013 + 2187) + (74 + 126) = 5200 + 200 = 5400.

Алгоритмы ускоренных вычислений
- Умножение на 11:
- Чтобы двузначное число, сумма цифр которого не превышает 10, умножить на 11, надо цифры этого числа раздвинуть и поставить между ними сумму этих цифр.
- Примеры:
- 72 * 11 = 7 (7 + 2) 2 = 792
- 35 * 11 = 3 (3 + 5) 5 = 385.
- Чтобы умножить на 11 двузначное число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить единицу, а вторую и последнюю (третью) оставить без изменения.
- Пример:
- 94 * 11 = 9 (9 + 4) 4 = 9 (13) 4 = (9 + 1) 34 = 1034.
- Вычитание путем уравнивания числа единиц последних разрядов уменьшаемого:
67 – 48 = ?
- Добавив к уменьшаемому 1, вычитаем 48 из 68, получаем 20. Отняв из этой разности ранее добавленную единицу, окончательно получаем 19.
67 – 48 = (68 – 48) – 1 = 20 – 1 = 19.
Уменьшив вычитаемое на 3, вычтем 313 из 453, получим 140. Отняв от этой разности еще 3, найдем 137.

Алгоритмы ускоренных вычислений
Умножение на число, оканчивающиеся на 5:
Алгоритм возведения в квадрат чисел, близких к 50:
- Чтобы четное двузначное число умножить на число, оканчивающееся на 5, можно применить следующее правило.
- Если один из сомножителей увеличить в несколько раз, а другой уменьшить во столько же раз, произведение не изменится.
- Пусть нужно возвести в квадрат число х , близкое к 50, но больше 50. Тогда х = 50 + а , где а – избыток числа х над 50.
Примеры:
х 2 = (50 + а ) 2 = 2500 + 100 а + а 2 = (25 + а ) * 100 + а 2 = (25 + х – 50) * 100 + а 2 = ( х – 25) * 100 + а 2 .
- 44 * 5 = (44 : 2) * 5 * 2 = 22 * 10 = 220;
- 28 * 15 = (28 : 2) * 15 * 2 = 14 * 30 =
- Отсюда следует алгоритм: если хочешь возвести в квадрат число, близкое к 50, но больше 50, то поступай так:
=420;
1) вычти из этого числа 25;
- 32 * 25 = (32 : 2) * 25 * 2 = 16 * 50 =
=800.
2) припиши к результату двумя цифрами квадрат избытка этого числа над 50.
Пояснение. 58 – 25 = 33, 8 2 = 64, 58 2 = 3364.
Пояснение. 64 – 25 = 39, 64 – 50 = 14, 14 2 = 196, 64 2 = 4096.
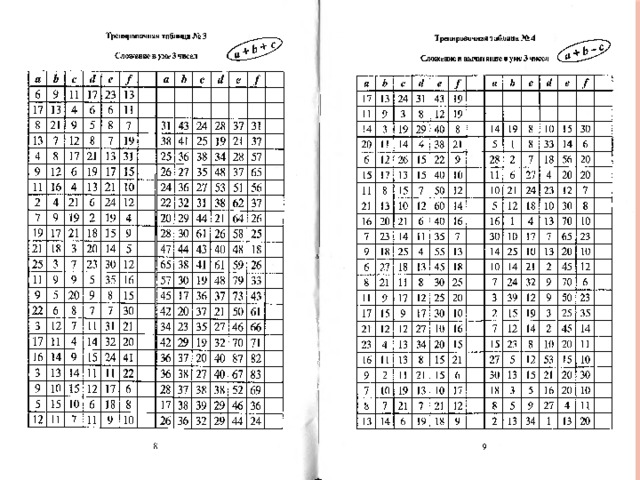

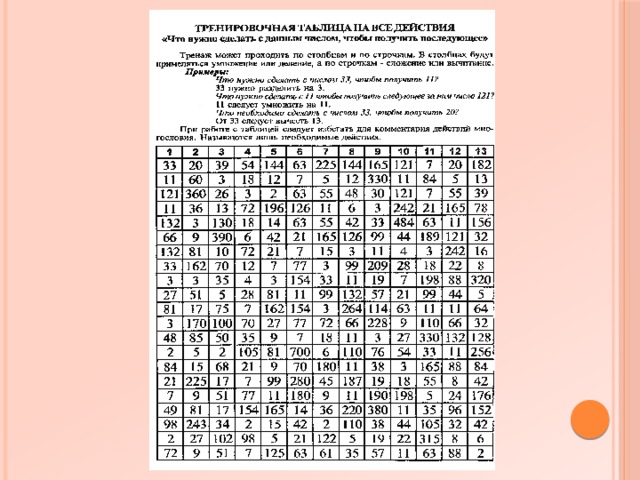



9.Работа с тренажерами
Работа с тренажерами значительно экономит время на уроке, учителю не нужно заранее, на перемене устные упражнения выписывать на доску. Учащиеся с тренажерами работают с удовольствием и интересом, в результате овладевают умениями и навыками, необходимыми для успешного изучения той или иной темы. Тренажеры также можно использовать при проведении зачетов по алгебре.

Решить пропорцию – значит найти неизвестный ее член.
Решите пропорцию.
Проверьте себя.
20 х = 100 · 5;
х = 2 5.
42 х = 7 · 5;

Решить пропорцию – значит найти неизвестный ее член.
Решите пропорцию.
Проверьте себя.
5 х = 34 · 20;
х = 136 .
7 х = 3 · 80;

Математический диктант
Проверьте себя:
Решите пропорцию :
1)
6
2)
3)
4)
60
5)
9
6)
21

Выразите процент десятичной дробью и обыкновенной дробью (обыкновенную дробь записывайте так: 2/3, если получилось ).
а ) 20% = = ;
б) 25% = = ;
в) 60% = = ;
г) 75% = = ;
д) 40% = = ;
е) 80% = = .
Проверь!

Четыре стрелка сделали по 60 выстрелов по мишени. У первого стрелка попадание в цель составило 80%, у второго - 55%, у третьего - 95%, у четвертого - 75%. Сколько раз каждый стрелок промахнулся?
%
Первый промахнулся раз;
Второй промахнулся раз;
Третий промахнулся раз;
Четвертый промахнулся раз.
%
Проверь!

Диагностика, мониторинг, тренинг и материалы для коррекции (уровневые тесты)

Контрольный устный входной тест для проверки качества знаний и определения уровня вычислительных навыков

Таблицы для коррекции знаний учащихся
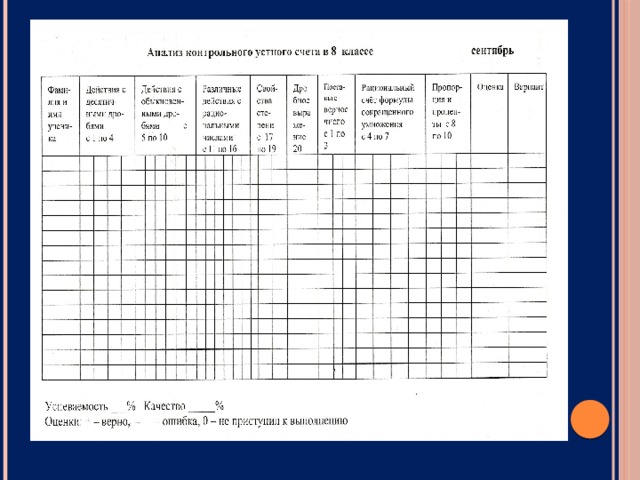
Заключение
- Подводя итоги разговора по теме «Использование устных упражнений на уроках математики», приведу еще несколько практических рекомендаций по проведению устной работы на уроке:
- • Начинать устную работу следует с более легкого упражнения, постепенно усложняя задания. Это делается, с одной стороны, для того, чтобы учащиеся постепенно втянулись в относительно быстрый ритм устной работы, а с другой – чтобы не подавить их инициативу и активность.
- • Продолжительность не должна превышать 10 минут (оптимально 7-8 минут).
- • Планировать устную работу лучше в конце подготовки конспекта, чтобы представлять весь урок в целом, его основные общие и конкретные задачи.
- • Устная работа – это прекрасное, активное, мобилизирующее, настраивающее на работу начало урока. Отчасти это связано с тем, что, как известно, в начале урока (приблизительно на третьей минуте) наступает первый кризис внимания школьников. Второй кризис внимания, как правило, бывает в середине урока (23-25 минут). В это время тоже хорошо отвлечь ребят несколькими уместными устными упражнениями.
- • Чтобы стимулировать активность, инициативу учащихся, дать возможность проявить себя, можно ввести соответствующую систему оценок во время устной работы (знаковую, балльную и т.д.).
- • В устной работе особенно ярко проявляется еще один аспект современного обучения – она дает возможность для формирования и развития диалоговой культуры учащихся, которая является элементом общей культуры современного человека. Она дает умение
вести диалог с собеседником, т.е. умение общаться, убеждать, слушать его. Это умение необходимо при ведении диалога с компьютером.





































![На рисунке изображен график квадратичной функции y=f(x) на отрезке [-5; 2]. Найдите f(-8) 7 6 5 4 3 2 1 ПОДУМАЙ! 1 1 -7 -6 -5 -4 -3 -2 -1 ПОДУМАЙ! 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 2 Не существует ВЕРНО! Повтор 3 5 ПОДУМАЙ! 4 10 Маленький тест 18](https://fhd.multiurok.ru/f/5/1/f516192b9fd88ee1de8af101605a690bce350947/img_phpjNUW1S_formirovanie-vychislitelnyh-navykov-na-urokah-matematiki_0_30.jpg)
 0, D0 х a0, D0 a0, D a0, D у у a0, D0 a0, D=0 a0, D=0 a0, D 0 х 0 х a0 a a a" width="640"
0, D0 х a0, D0 a0, D a0, D у у a0, D0 a0, D=0 a0, D=0 a0, D 0 х 0 х a0 a a a" width="640"






































