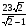Тема: «Формула суммы первых n членов геометрической прогрессии»
Класса: 9
Цель урока:
Обучающая: формирование знаний и первичное закрепление умений по теме «Формула суммы n первых членов геометрической прогрессии»
Развивающая: развитие навыков логического мышления; развитие вычислительных навыков; развитие умений обобщать и конкретизировать знания при решении заданий.
Воспитательная: воспитание воли и настойчивости для достижения конечных результатов; воспитание наблюдательности.
Номер урока в теме: 1
Тип урока: Урок изучения новых знаний.
Технологии обучения: урок-лекция, проблемное,
Формы организации учебной деятельности: Индивидуальная, фронтальная, коллективные способы обучения
Оборудование урока: компьютер и мультимедийное оборудование;
Методическое сопровождение: компьютерная презентация
ПЛАН УРОКА
| Блоки | Этапы урока | Время |
| 1 | |
8 мин. |
| 2 | Основная часть: |
22 мин. |
| 3 | Домашнее задание и рекомендации по его выполнению | 2 мин. |
| 4 | Подведение итогов урока: - выполнение Теста - достижения - рефлексия | 8 мин. |
1.Постановка целей урока
Класс делится на 2 группы (2 ряда).
Урок начинается с постановки задач перед учащимися. В беседе учитель акцентирует внимание на том, что материал урока дает им возможность развивать умения находить закономерности, применять полученные знания при решении нестандартных задач. Учащимся сообщается план проведения урока
2.Устная работа
Вопросы
В третьем тысячелетии високосными годами будут 2008, 2012 ,2016, 2020 продолжите, в какой последовательности записаны года?
У семи лиц по семи кошек, каждая кошка съедает по семи мышек, каждая мышь съедает по семи колосьев ячменя, из каждого колоса может вырасти по семи мер ячменя. Как велики числа этого ряда? (16807)
Работа с сигнальными карточками
На каждой парте находятся карточки с формулами. Учитель называет формулу, дети, молча, поднимают карточку.
| �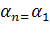 �+(n-1)d �+(n-1)d |
| Sn=�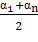 �n �n |
| d=�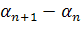 � � |
| 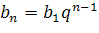
|
| q=�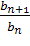 � � |
|
|
Учитель:
Формула n-го члена арифметической прогрессии.
Формула n-го члена геометрической прогрессии.
Формула суммы n-первых членов арифметической прогрессии
Формула для нахождения разности арифметической прогрессии
Формула для нахождения знаменателя геометрической прогрессии
Поднимите нужные формулы, которые будут использоваться при решении задач №6, взятых из открытого банка ГИА.
| Задание 6 (№ 169715) | 
| 
| Начало формы 
Конец формы |
| Элементы содержания: | 4.2 |
| | Умения: | 4.5 4.6 | | Прототип: | 137306, аналогичные задания, все прототипы 6 |
|
| Последовательность задана условиями 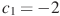 , , 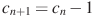 . Найдите . Найдите 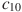 . . |
| Задание 6 (№ 169675) | 
| 
| Начало формы 
Конец формы |
| Элементы содержания: | 4.2 |
| | Умения: | 4.5 4.6 | | Прототип: | 137305, аналогичные задания, все прототипы 6 |
|
| Арифметическая прогрессия задана условиями: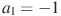 , ,  . Какое из данных чисел является членом этой прогрессии? . Какое из данных чисел является членом этой прогрессии? Варианты ответа | 1. | -22 |
| 2. | -23 |
| 3. | -24 |
| 4. | -20 |
|
В таблице, составленной нами ранее, не заполнена 1 ячейка. Наша задача на сегодняшнем уроке заполнить этот пробел.
3. Историческая справка
Индийский царь Шерам, впервые познакомившись с шахматами, восхитился их своеобразием и обилием красивых комбинаций. Узнав, что замечательную игру изобрёл его подданный Сета, царь призвал к себе мудреца, желая лично наградить за выдумку. Властелин обещал выполнить любую его просьбу и был удивлен, когда тот попросил лишь некоторое количество пшеничных зёрен. На первое поле доски он попросил положить одно зерно, на второе – два и так далее: на каждое последующее поле нужно было класть вдвое больше зерен, чем на предыдущее. Царь распорядился побыстрее выдать изобретателю его ничтожную награду. Однако на следующий день придворные математики сообщили своему повелителю:
«Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зёрен, какое потребовал Сета. Нет его и в житницах всего государства. Не найдётся такого числа зёрен и на всём пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажите растопить льды и снега, покрывающие далёкие северные пустыни. Пусть всё пространство их сплошь будет засеяно пшеницей. И всё то, что родиться на этих полях, прикажи отдать Сете. Тогда он получит свою награду».
С изумлением внимал царь словам старца.
Мудрец скромно потребовал…
Число зерен, о которых идёт речь, является суммой шестидесяти четырех членов геометрической прогрессии, первый член которой равен 1, а знаменатель равен 2. обозначим эту сумму через S:
Умножим обе части записанного равенства на знаменатель прогрессии, получим:
Вычтем почленно из второго равенства первое и проведём упрощение:
1 + 2 + 22 + … + 263 = 264 - 1 зерно. Это число записывается двадцатью цифрами и фантастически велико.

18 квинтиллионов 446 квадриллионов
744 триллиона 73 миллиарда
709 миллионов 551 тысяча 615 зерен
4.Актуализация новых знаний.
Выведем теперь формулу суммы n-первых членов произвольной геометрической прогрессии. Воспользуемся тем же приёмом, с помощью которого была вычислена сумма S.
Пусть дана геометрическая прогрессия (bn). Обозначим сумму п первых её членов через Sn:
Sn=b1+b2+b3+…+bn-1+bn. (1)
Умножим обе части этого равенства на q:
Snq=b1q+b2q+b3q+…+bn-1q+bnq.
Учитывая, что b1q=b2, b2q=b3, b3q=b4, …, bn-1q=bn,
Получим Snq=b2+b3+b4+…+bn+bnq. (2)
Вычтем почленно из равенства (2) равенство (1) и приведём подобные члены:
Snq – Sn=( b2+b3+…+bn+bnq) – (b1+b2+…+bn-1+bn)=bnq – b1.
Sn (q – 1)=bnq – b1.
Отсюда следует, что при q ≠ 1
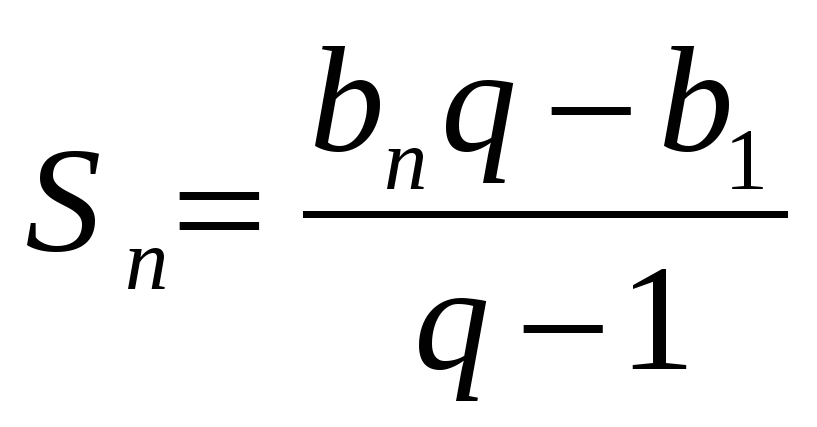 . (I)
. (I)
Мы получили формулу суммы п первых членов геометрической прогрессии, в которой q ≠ 1. Если q=1, то все члены прогрессии равны первому члену и Sn=nb1.
При решении многих задач удобно пользоваться формулой суммы п первых членов геометрической прогрессии, записанной в другом виде. Подставим в формулу (I) вместо bn выражение b1qn – 1. Получим:
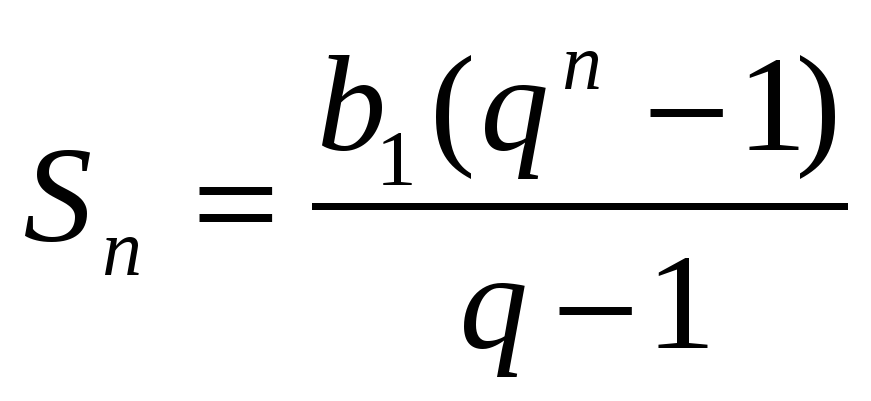 , если q ≠ 1. (II)
, если q ≠ 1. (II)
Учитель
1 задача : Найдем сумму первых десяти членов геометрической прогрессии ( bn), которой b1=3 и q=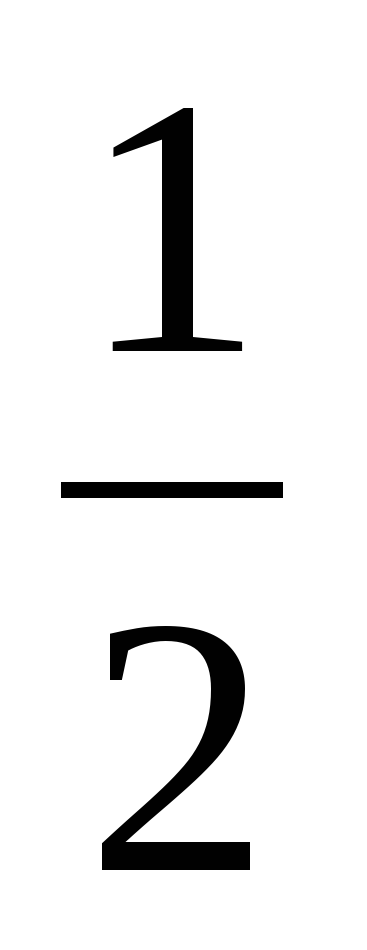 .
.
Т.к. известны первый член и знаменатель прогрессии, то удобно пользоваться формулой (II). Получим:
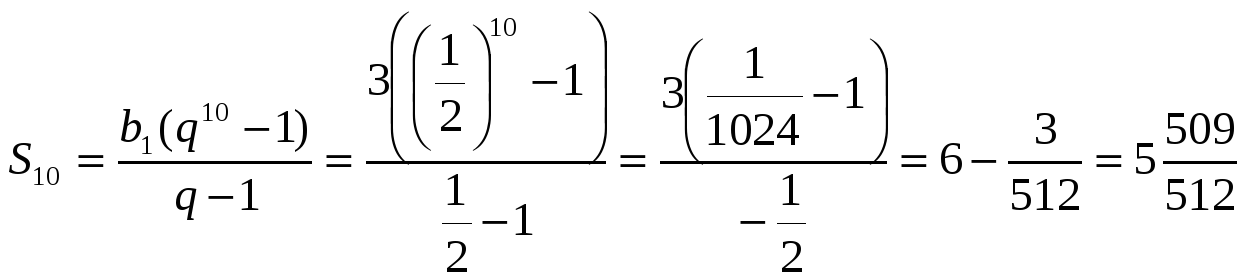
5.Решение задач по группам.
Учитель раздает каждой группе 5 задач и объясняет задание.
| 1 группа | 2 группа |
| 1) b1=2 и q=2.Найти S | 2) 6) b1=3 и q=-2. Найти S |
| 3) №648 (а) | 4) № 648 (б) |
| 5) № 649 (а) | 7) №649 (в) |
| 8) № 649 (б) | 9) № 649 (г) |
| 10) Каждое простейшее одноклеточное животное инфузория-туфелька размножается делением на 2 части. Сколько инфузорий было первоначально, если после шестикратного деления их стало 320? q=2�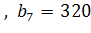 �,� �,�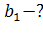 � � | 11) Рост дрожжевых клеток происходит делением каждой клетки на две части. Сколько стало клеток после их десятикратного деления, если первоначально было 6 клеток. �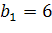 � , q=2� � , q=2�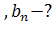 � � �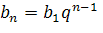 �клетки делились 10 раз, значит надо найти � �клетки делились 10 раз, значит надо найти �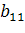 � � |
Ответы
| 1 группа | 2 группа |
| 1) Отв: 30 | 2)6) Отв:-15 |
| 3) №648 (а) Отв 15,5 | 4) № 648 (б) Отв: 624,8 |
| 5) № 649 (а) Отв: -63 | 7) №649 (в) Отв:-63 |
| 8) № 649 (б) Отв: 147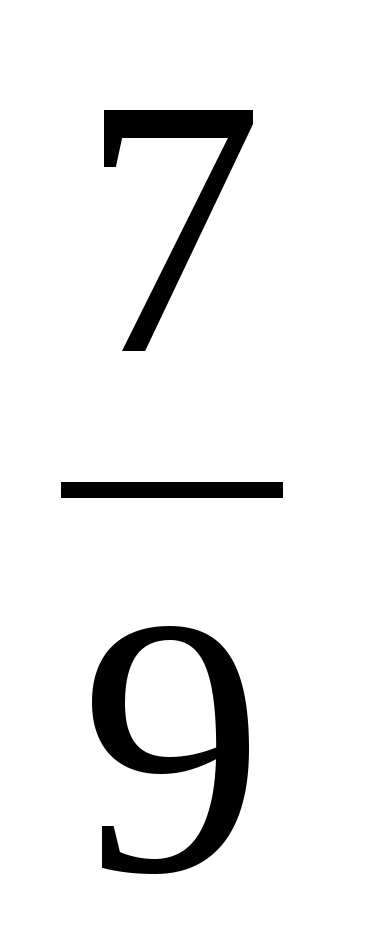 | 9) № 649 (г) Отв: 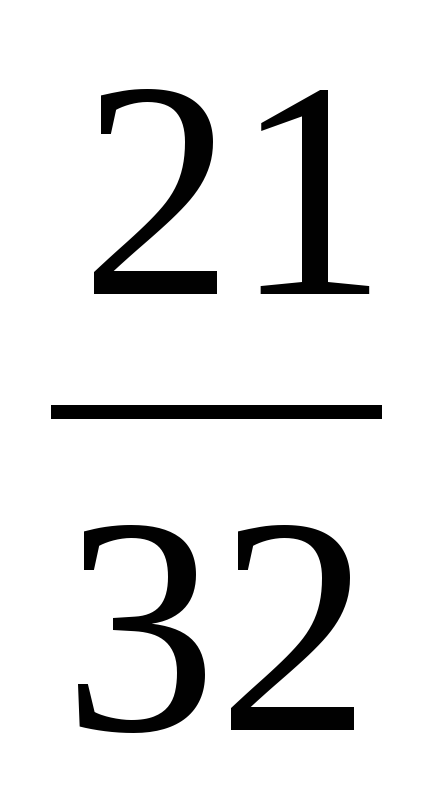 |
| 10) Отв 5 | 11) Отв: 6144 |
Перед вами пять задач. Каждой группе предложено обсудить решение 5-ой задачи. В течение 5 минут вы обсуждаете задачу и предлагаете ее решение. Затем один из группы выходит к доске и записывает решение задачи. При записи задачи на доске, весь класс записывает решение в свои тетради. У каждой группы на парте есть ватман, вы можете сделать к задаче пояснительную схему.
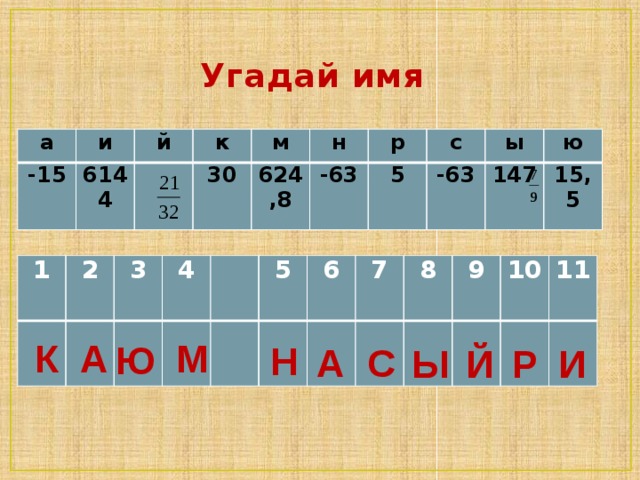
6. Угадай имя Кроме этого, номер задачи соответствует букве, которая записывается в окошечко с тем заданием каждой группы. Если не допущено ошибок, то в итоге получиться имя выдающегося татарского просветителя, 189 –лет которого отметили в этом году 14 февраля.
| а | и | й | к | м | н | р | с | ы | ю |
| -15
| 6144 | 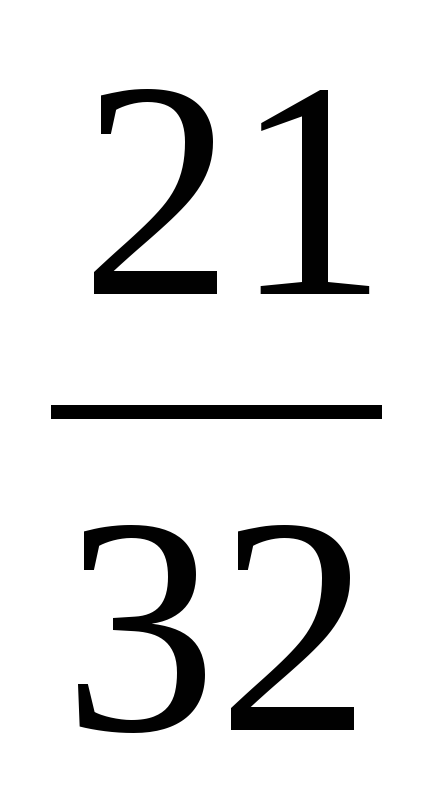
| 30 | 624,8 | -63 | 5 | -63 | 147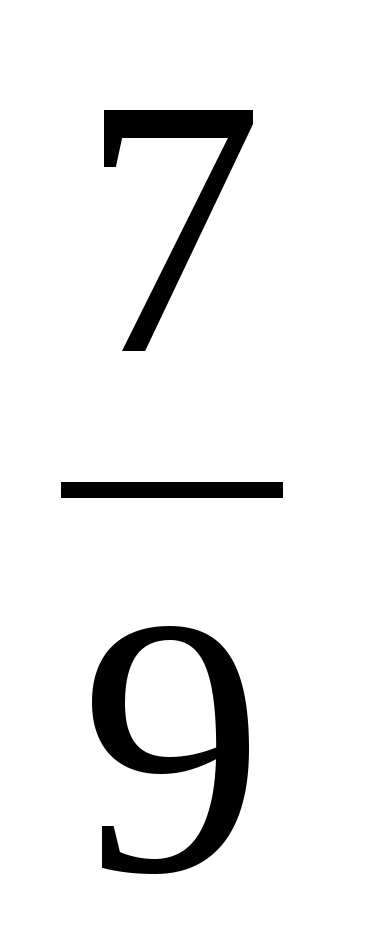 | 15,5 |
Если не допущено ошибок, то в итоге получиться имя. (Каюм Насыйри)
Учитель: Получилось имя «Каюм Насыйри». Мне хотелось прочитать слова К.Насыйри, изложенные в его книге « Воспитание».
Наставление тридцать четвертое. О сын мой, когда придется тебе воспитывать детей, будь особенно старателен, пока они малы. Знания, полученные в детстве, подобны орнаменту, выбитому на камне. Прут легче гнется, покуда тонок. В нежном возрасте следует внушать понятия о многих науках и давать кое-какие знания даже по математике. В другой раз мы поговорим об этом подробнее.
Наставление сорок восьмое. Не кичись здоровьем и не обманывай себя благополучием прежних дней, о сын мой. Всегда здоровым быть нельзя. Поэтому береги себя и не доводи до скотства. Знай, что здоровье сохранит лишь тот, кто следует многим заповедям.
Наставление сорок девятое. Что посеешь, то и пожнешь, о сын мой. Это значит, что за добро тебе воздастся добром, а за зло ты заслужишь лишь страдания и муки.
7. Физкультминутка.
Гимнастика для глаз.
Я буду называть последовательность. Если арифметическая прогрессия, то 2 раза поднять обе руки, если геометрическая прогрессия, то подпригиваем 4 раза.
1) 1,2,3, 4, ...
2) 5, 25, 125, 625,..
3) 1, 3, 8, 10, ...
4) 2. 4, 8, 16, 32,..
7. Решение тестов
| «3» | «4» | «5» |
| 1. b3 =12, b5 =48 q-? A) 4 Б) -4;4 В) -2 Г) -2;2 | b4 =25, b6 =16 q-? A) 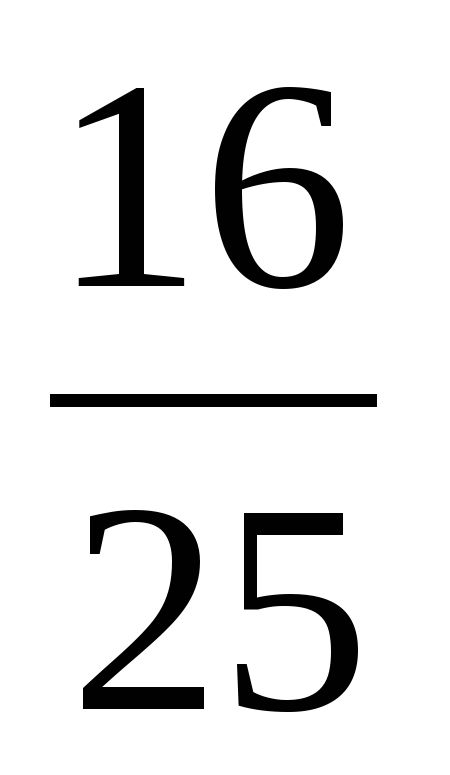 Б) 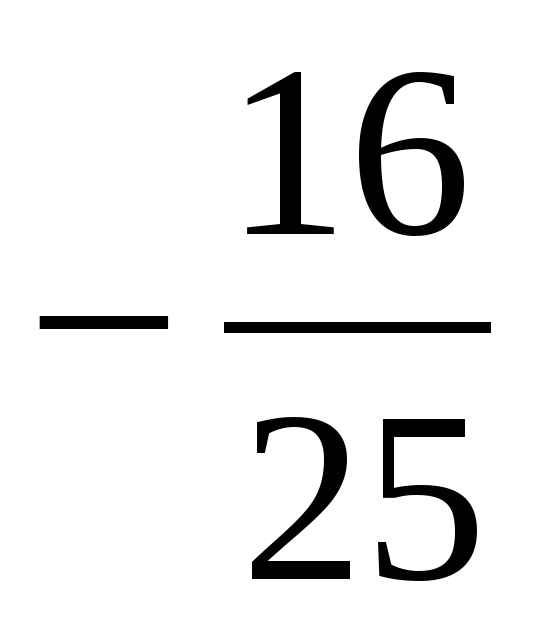 ; ;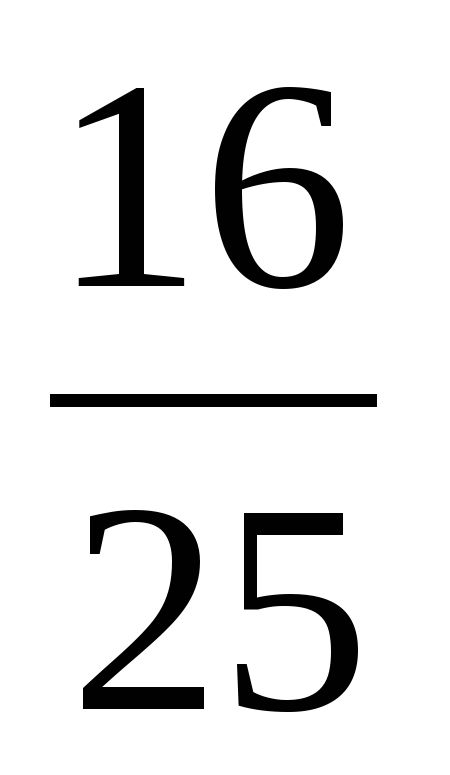 В) 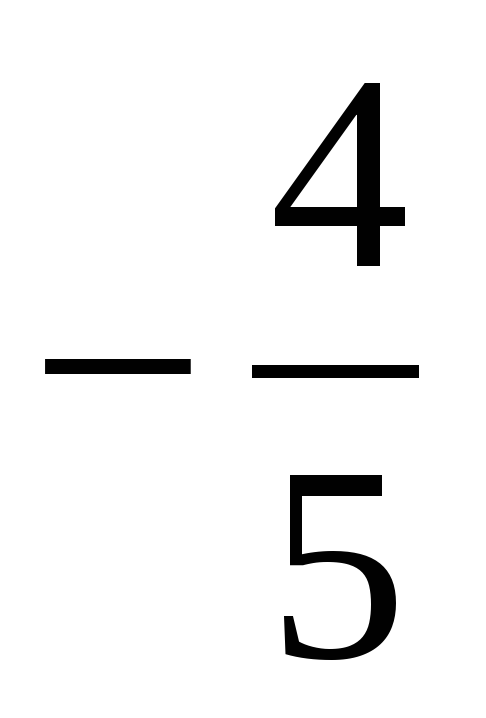 Г) 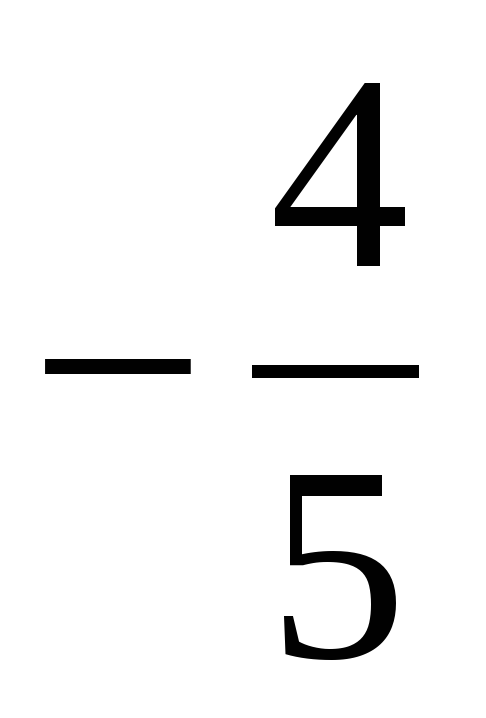 ; ;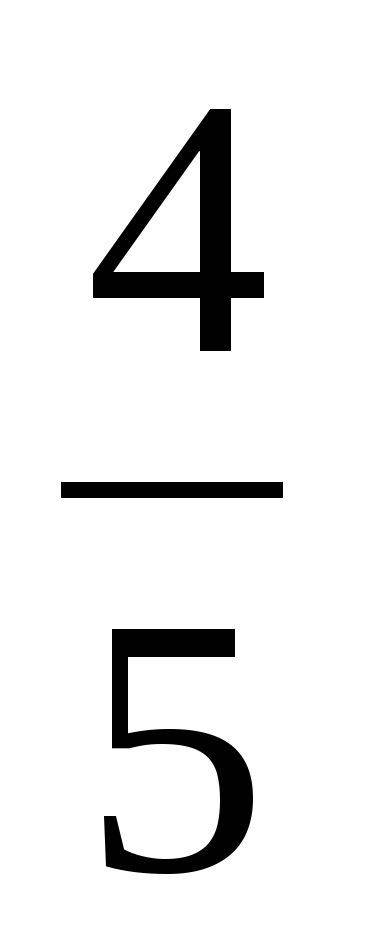 | b12 =315, b14 =317 q-? A) 9 Б) -9;9 В) -3 Г) -3;3 |
| 2. Изданных геометрических прогрессий выберите ту, среди которой есть число 5. A) an = -3n Б) an = 3n В) 3*2n-1 Г) an = 2*3n-1 | 2. Последовательности заданы несколькими первыми членами. Одна из них геометрическая прогрессия. Укажите A) 1;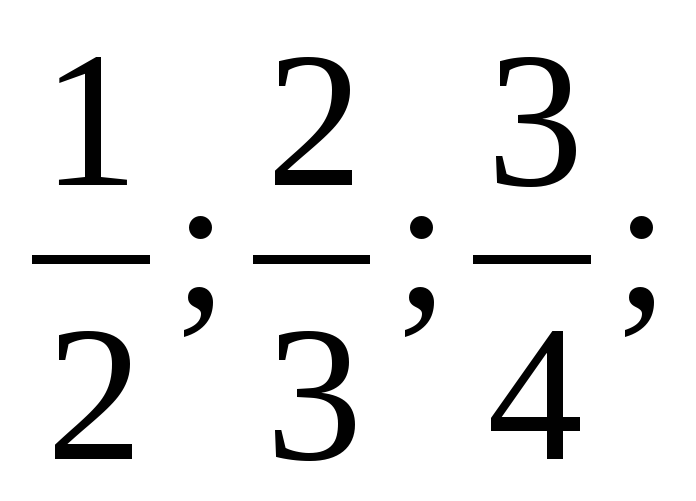 … … Б) 1;3;5;7;… В) 1;2;4;8;… Г) 1;2;3;5;… | 2. В геометрической прогрессии b5=12 b7 =27 b6 -? A) 19,5 Б) 25 В) 18 Г) 36 |
| 3. b1 =64, q=2 S5-? A) 64 Б) 1984 В) 128 Г) 192 | 3. b1 =10, q=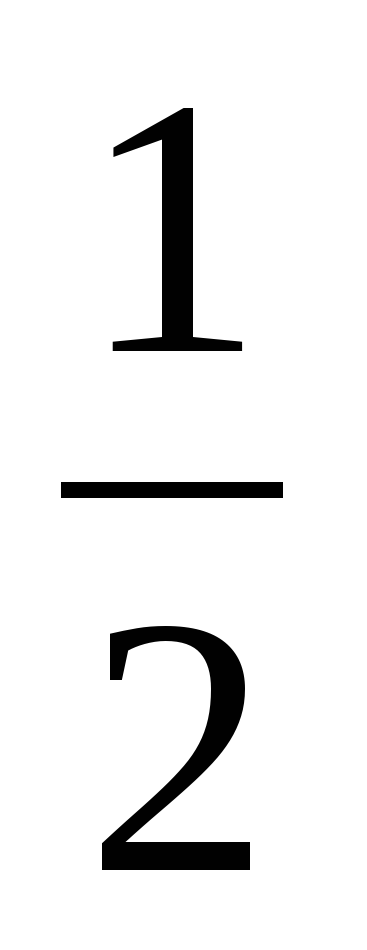 S4-? S4-? A) 187,5 Б) 16,75 В) 18,75 Г) -18,75 | 3. b1 =3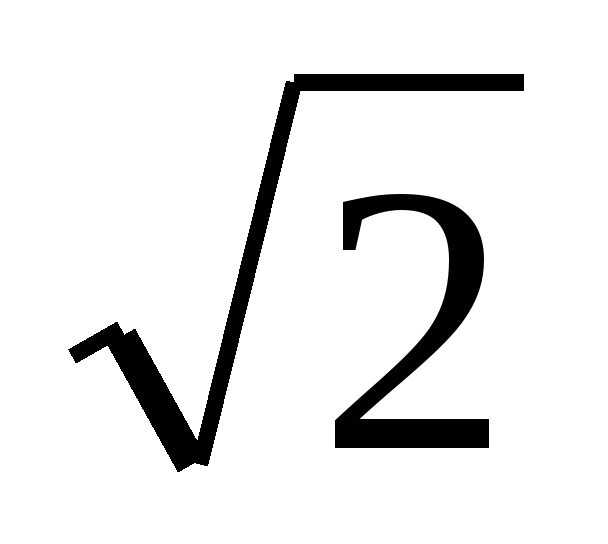 , q= , q=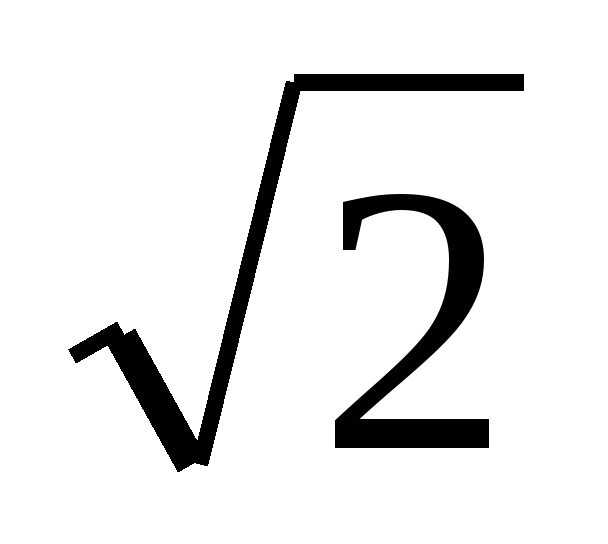 S6-? S6-? A) 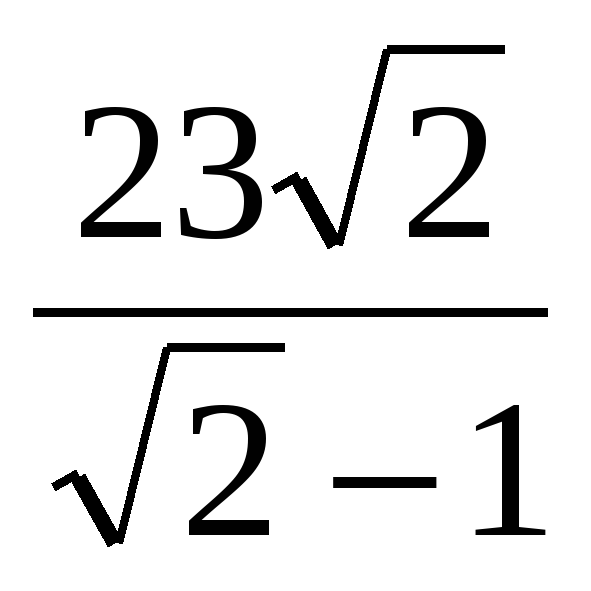 Б) 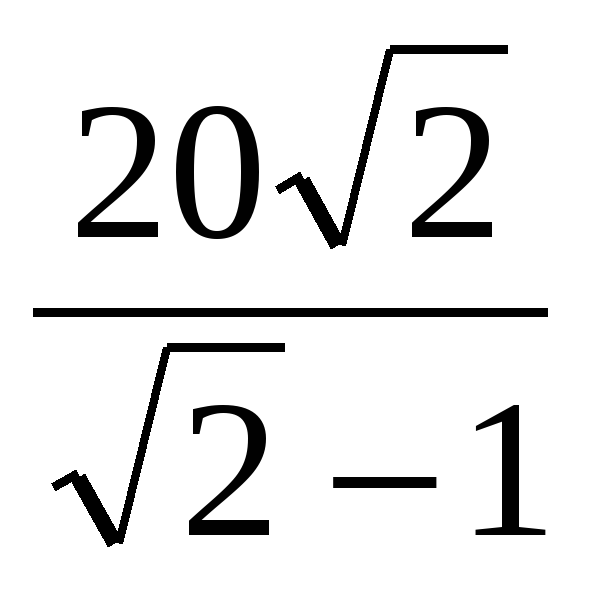 В) 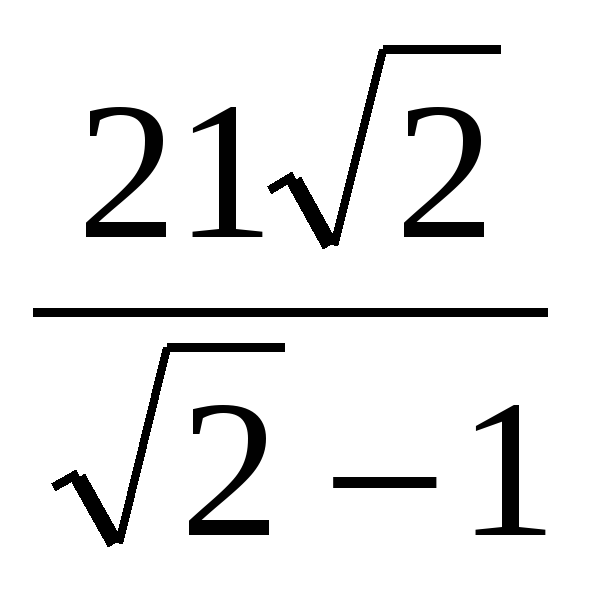 Г) 21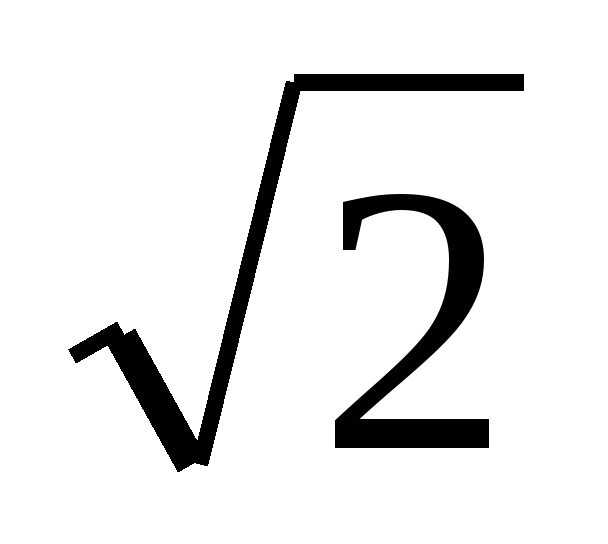 |
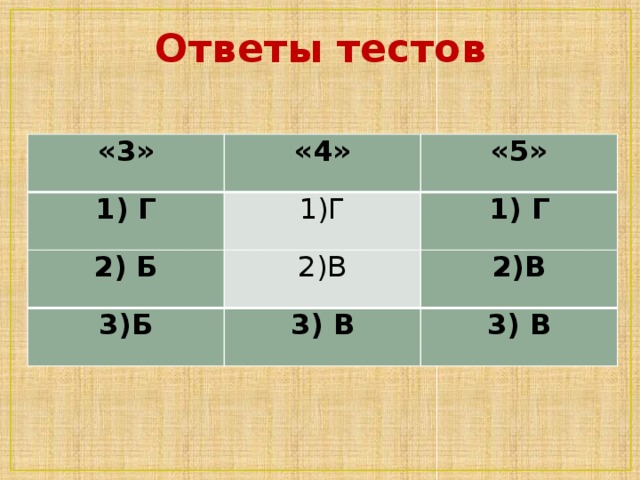
Ответы тестов
| 3 | 4 | 5 |
| 1) Г | 1)Г | 1) Г |
| 2) Б | 2)В | 2)В |
| 3)Б | 3) В | 3) В |
8.Проверка теста слайд №4
9. Рефлексия. Покажите любую формулу напечатанную, если вам что-то осталось непонятным или не понравилось. И покажите написанную любую формулу сумму n членов геометрической прогрессии.
10.Итог урока. Учитель подводит итоги урока, выставляет оценки.
Литература
Ю.Н. Макарычев, Н.Г. Миндюк. К.И. Нешков, с. Б Суворова; под ред. С.А. Теляковского. Алгебра. Учебник для 9 кл. общеобразовательных учреждений. Москва. «Просвещение» 2013 г.
Лысенко Ф. Ф. Алгебра 9кл. Итоговая аттестация. Ростов-на-Дону. Издательство «Легион» 2013г.
Банк открытых заданий для подготовки к ГИА.
Интересные факты
1) Химия. При повышении температуры по арифметической прогрессии скорость химических реакций растет по геометрической прогрессии.
2) Геометрия. Вписанные друг в друга правильные треугольники образуют геометрическую прогрессию.
3) Физика. И в физических процессах встречается эта закономерность. Нейтрон, ударяя по ядру урана, раскалывает его на две части. Получаются два нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывает их еще на 4 части и т.д. – это геометрическая прогрессия.
4) Биология. Микроорганизмы размножаются делением пополам, поэтому при благоприятных условиях, через одинаковый промежуток времени их число удваивается.
5)Экономика. Вклады в банках увеличиваются по схемам сложных и простых процентов. Простые проценты – увеличение первоначального вклада в арифметической прогрессии, сложные проценты – увеличение в геометрической прогрессии.







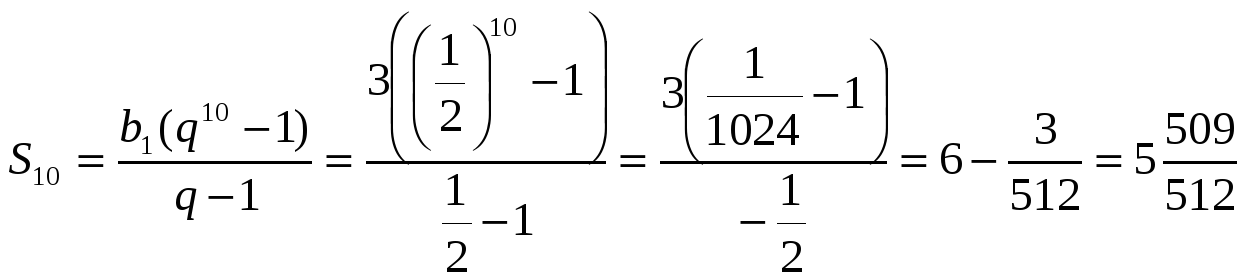
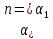
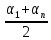 n
n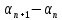
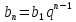
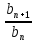
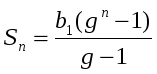
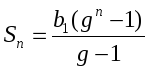
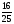
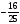 ;
;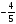
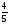
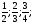 …
…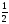
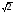 ,
,