Урок алгебры в 9 классе. Автор учебника Макарычев Ю.Н. Учитель Гончарова Е.Б.
Тема: «Формула суммы п первых членов геометрической прогрессии».
Цели: совершенствовать умения и навыки применения формулы суммы первых п членов геометрической прогрессии при решении задач; проводить подготовку к ОГЭ.
Ход урока
I. Организационный момент.
II. Проверка усвоения изученного материала.
-
Проверка д/з.
№3 Бизнесмен Коржов получил в 2000 году прибыль в размере 1 400 000 рублей. Каждый следующий год его прибыль увеличивалась на 20% по сравнению с предыдущим годом. Сколько рублей составила прибыль Коржова за 2004 год?
Решение.
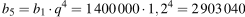
Ответ: 2 903 040.
№4 Вере надо подписать 640 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Вера подписала 10 открыток. Определите, сколько открыток было подписано за четвертый день, если вся работа была выполнена за 16 дней.
Решение.
В первый день Вера подписала а1 =10 открыток, во второй –а2 , …, в последний - ап открыток . Всего было подписано 640 открыток. Если количество подписываемых открыток увеличивалось на d каждый день, то
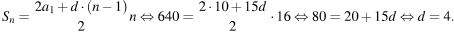
Тогда 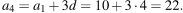
Следовательно, за четвертый день было подписано 22 открытки.
Ответ: 22.
-
Устная работа.

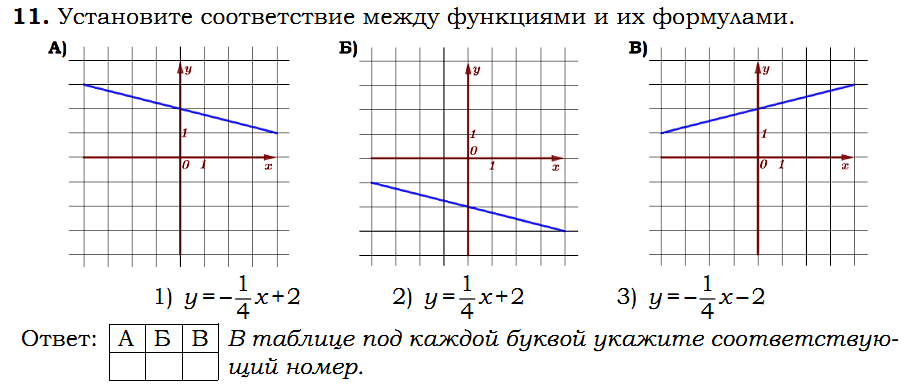
III. Формирование умений и навыков.
1. Найдите девятый член геометрической прогрессии (bп), если
b1 = 100000 и q = 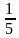 .
.
2. Первый член геометрической прогрессии (bп) равен 6, а знаменатель равен 4. Найдите сумму пяти первых членов этой прогрессии.
3. Между числами 35 и 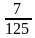 вставьте три числа так, чтобы вместе с данными они образовывали геометрическую прогрессию.
вставьте три числа так, чтобы вместе с данными они образовывали геометрическую прогрессию.
4. Найдите сумму пяти первых членов геометрической прогрессии (bп) с положительными членами, зная, что b3 = 3,6 и b5 = 32,4.
5. Найдите первый член геометрической прогрессии (ап), в которой q = 2, S5 = 403.
Решение.
1. (bп) – геометрическая прогрессия, b1 = 100000, q = 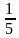 .
.
b9 = b1 · q8, 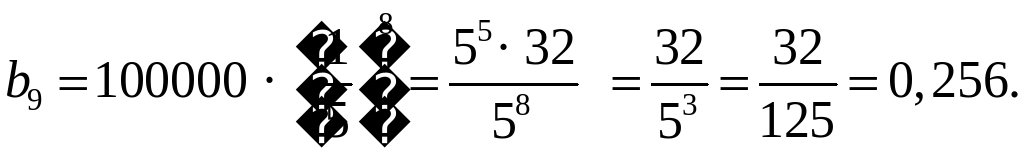
О т в е т: 0,256.
2. (bп) – геометрическая прогрессия, b1 = 6, q = 4.
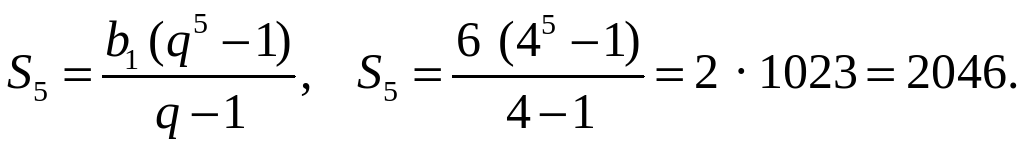
О т в е т: 2046.
3. 35; а2; а3; а4; 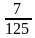 – геометрическая прогрессия,
– геометрическая прогрессия,
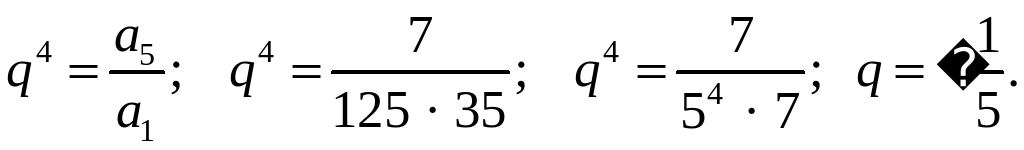
1) 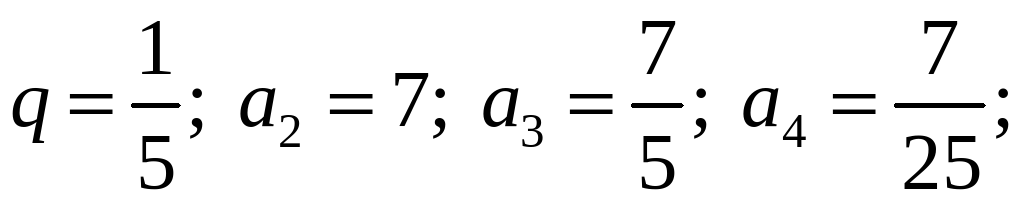
2) 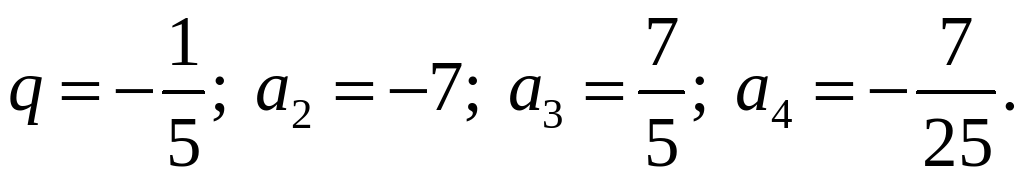
О т в е т: 1) 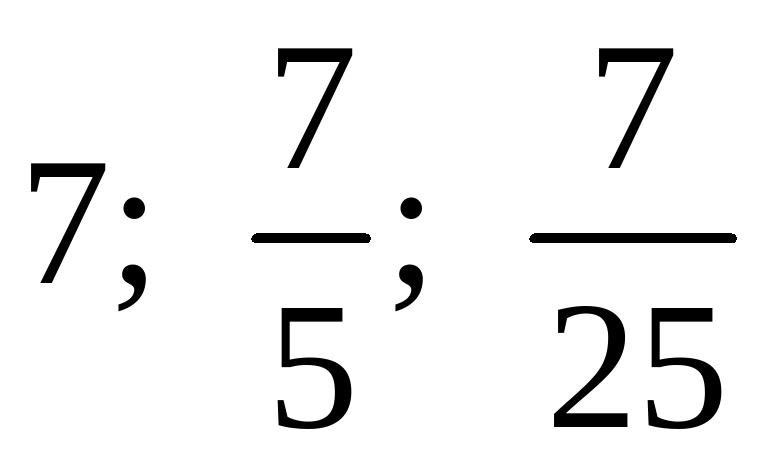 ; 2)
; 2) 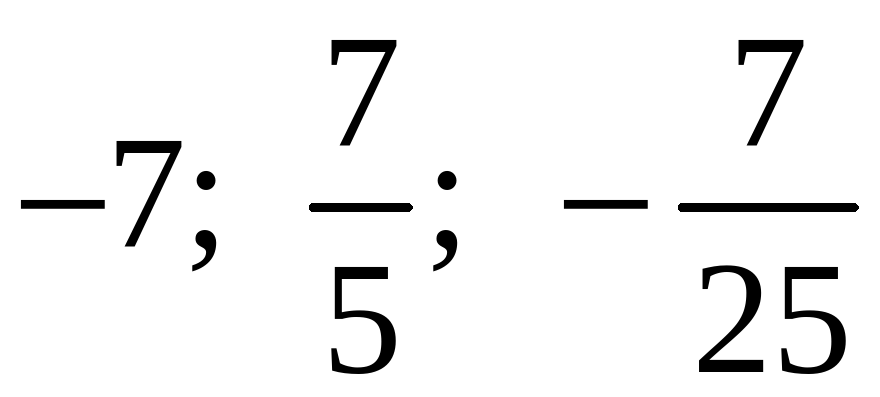 .
.
4. (bп) – геометрическая прогрессия, bп 0, b3 = 3,6, b5 = 32,4.
b3 = b1 · q2;
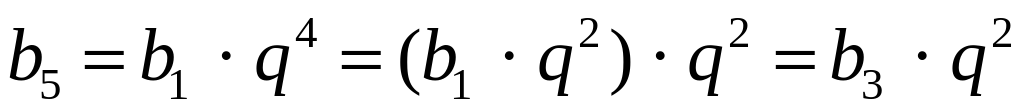 ;
;
32,4 = 3,6 · q2; q2 = 9; q = 3 (так как bп 0);
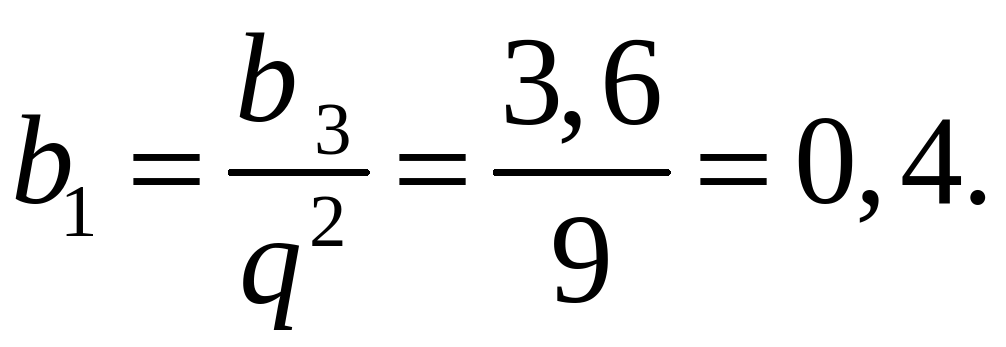
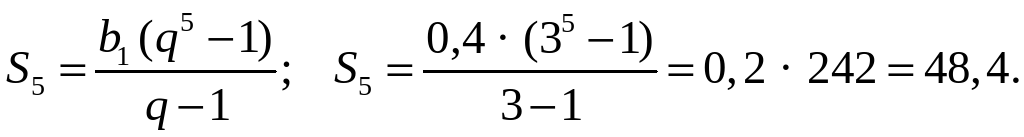
О т в е т: 48,4.
5. (ап) – геометрическая прогрессия, q = 2, S5 = 403.
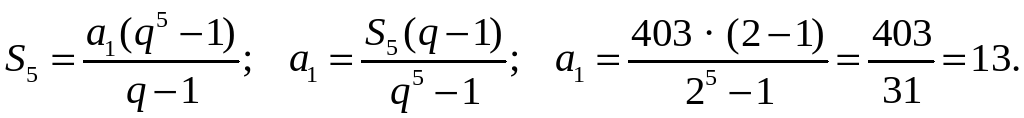
О т в е т: 13.
IV. Самостоятельная работа.
В а р и а н т 1
1) Найдите пятый член геометрической прогрессии (bn), в которой b1 = 5, q =-3.
2) (ап) – геометрическая прогрессия. Найдите S4, если а1 = 3, q = –2.
3) Найдите сумму шести первых членов геометрической прогрессии 5; –2,5; … .
В а р и а н т 2
1) Найдите шестой член геометрической прогрессии (bn), в которой b1 =3, q =- 2.
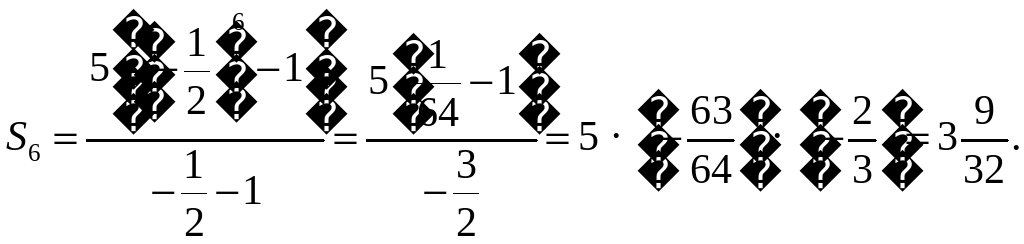
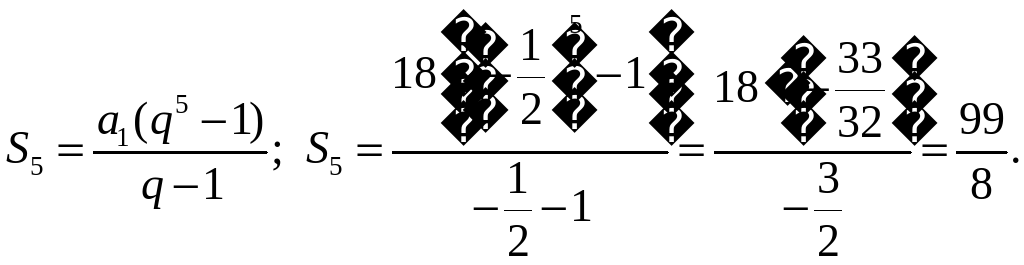
2) (aп) – геометрическая прогрессия. Найдите S5, если а1 = 18, q = – 0,5.
3) Найдите сумму пяти первых членов геометрической прогрессии 1,5; –3; … .
Решение.
Вариант 1
1) 5 · 81 = 405
2) 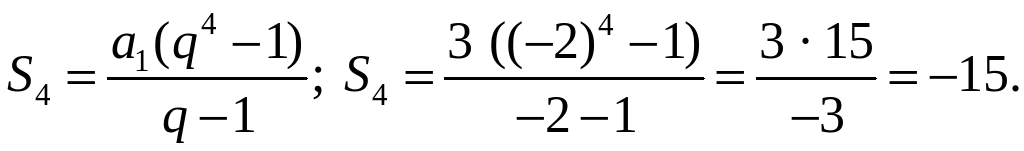
3) 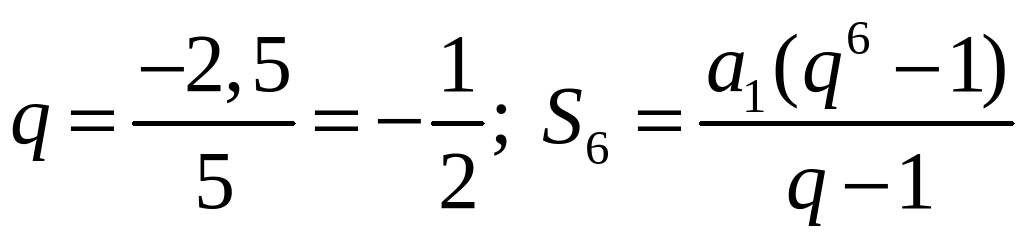
Вариант 2
1) 3 · (-32) = -160
2) 
3) 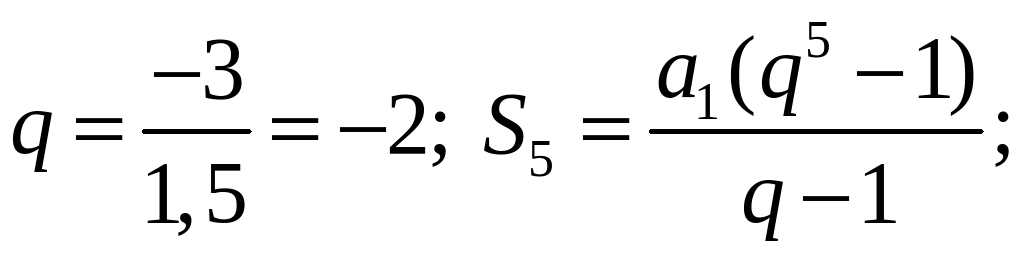
V. Итог урока, рефлексия.
Домашнее задание.
П. 27, 28 №705(б), 710(б, г), №3, 4.
№3
№4
Дополнительно.









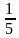 .
.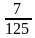 вставьте три числа так, чтобы вместе с данными они образовывали геометрическую прогрессию.
вставьте три числа так, чтобы вместе с данными они образовывали геометрическую прогрессию.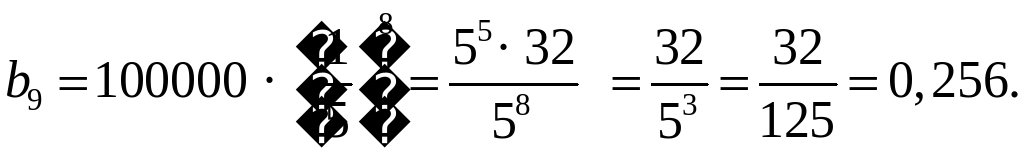
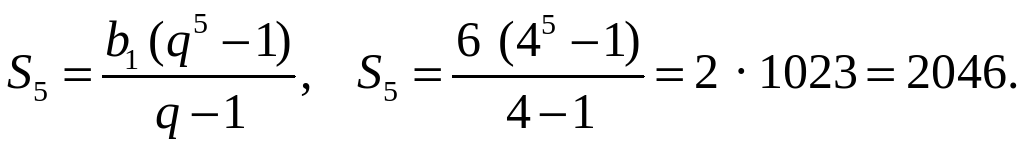
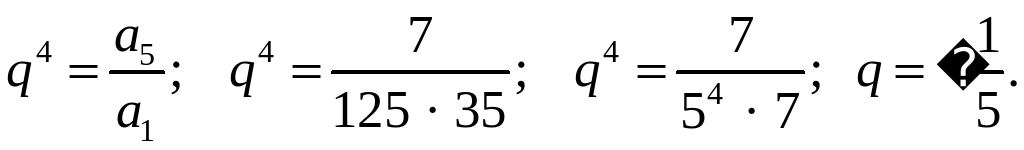
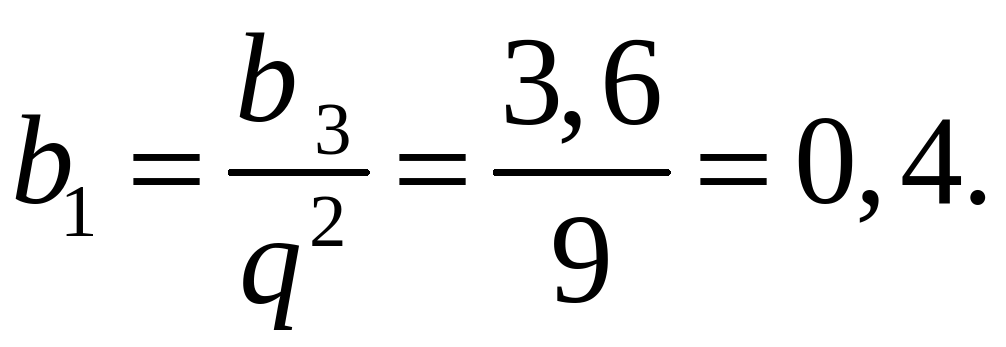
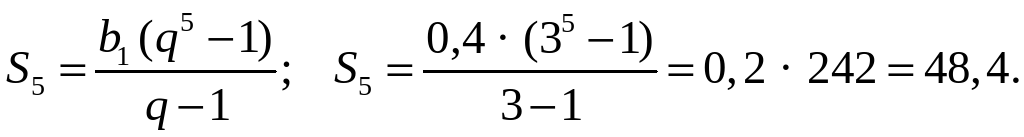
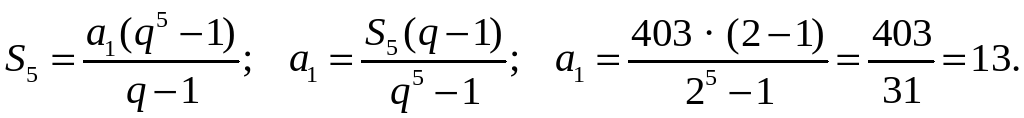
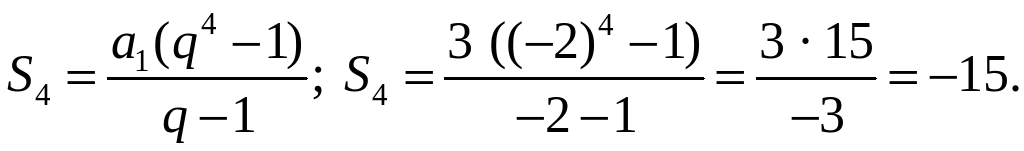
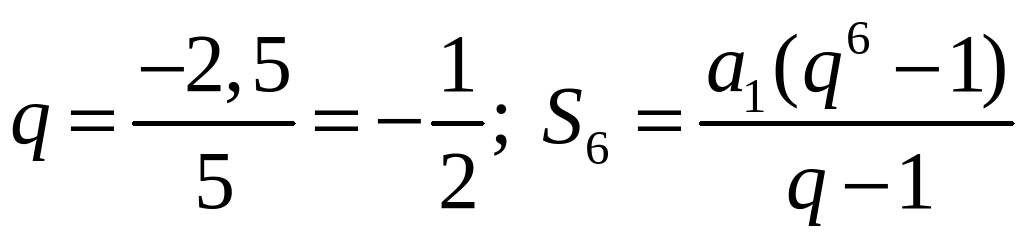


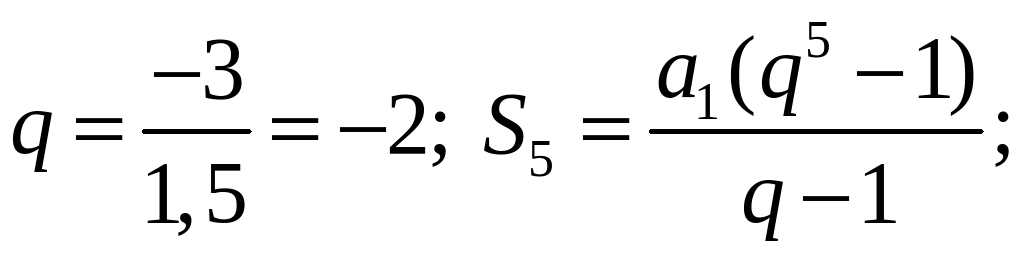







Алгебра 11 класc
Русская литература 11 класс ФГОС. Часть...
Алгебра 11 класс ФГОС
Подготовка к ОГЭ по физике. Часть 1.
Электронная тетрадь окружающий мир 4...
Подготовка к ЕГЭ по английскому языку....
История России 6 класс ФГОС
Электронная тетрадь по информатике 10...
© 2021, Гончарова Евгения Борисовна 638 28
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы