Украина, Донецк
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 26.02.2024 20:20
Мигинская Людмила Михайловна
учитель математики
73 года
759
62 456 
Местоположение
Специализация
Формулы двойного угла
Категория:
Алгебра
22.11.2018 17:43
Просмотр содержимого документа
«Формулы двойного угла»
Урок по теме: «Формулы двойного угла»
Цели урока:
Образовательные:
Формирование предметных компетенций (вывод формул двойного угла) на основе ранее сформированных компетенций: формул сложения тригонометрических функций.
Развивающие: Развивать практические навыки применения формул двойного угла при решении упражнений;
Воспитательные: Воспитание навыков самоконтроля и взаимоконтроля.
Тип урока: ознакомление с новым материалом
Форма организации учебной деятельности: фронтальная, индивидуальная.
Методы урока: Объяснительно – иллюстративный.
Средства обучения:
Рабочая тетрадь, проектор, разноуровневый раздаточный материал для обучающей самостоятельной работы.
Ход урока
Организационный момент. Мотивационная беседа с последующей постановкой цели урока.
На предыдущих уроках мы говорили о формулах сложения синуса, косинуса, тангенса двух углов. Сегодня мы продолжим разговор о данных формулах и с их помощью получим еще несколько новых формул. А также научимся применять вновь изученные формулы при решении упражнений.
Повторим ранее пройденный материал.
2.Актуализация опорных знаний. Подготовка учащихся к активному и сознательному усвоению нового материала. Устная работа.
Определите знак тригонометрического выражения:
Записи на доске:
1). sin365°, ctg3п/4 , cos(−91°), sin235°, cos 2п/3, tg34°, tg(−124°)
2). Определите, какой четверти принадлежит угол 𝛼. Приведите примеры.
𝑐o𝑠𝛼 0, 𝑠in𝛼 tg𝛼 0, 𝑐o𝑠𝛼
ctg𝛼 in𝛼 0;
3). Запишите формулы:𝑐o𝑠(𝛼 + 𝛽) =
𝑠in(𝛼 + 𝛽) =
tg(𝛼 + 𝛽) =
3. Изучение нового материала – самостоятельный вывод формул sin2x, cos2x, tg2x.( У доски)
Для получения новых формул мы воспользуемся формулами сложения. Итак, давайте в формуле: sin (∝ +𝛽) = 𝑠in𝛼 ∙ 𝑐o𝑠𝛽 + 𝑐o𝑠𝛼 ∙ 𝑠in𝛽 Предположим, что 𝛽 = 𝛼 , делаем замену, получаем Sin2∝ = 𝑠in𝛼 ∙ 𝑐o𝑠𝛼 + 𝑐o𝑠𝛼 ∙ sin𝛼 = 2𝑠in𝛼 ∙ 𝑐o𝑠𝛼sin2a = 2sina • cosa
Также выведем формулу cos2 𝛽 = 𝑐o𝑠𝛼 ∙ 𝑐o𝑠𝛽 − 𝑠in𝛼 ∙ 𝑠in𝛽
cos2𝛼=cos2 𝛼 – sin 2 𝛼Эти формулы называются - формулами двойного угла.
Формулу tg2 a вывести в тетрадях самостоятельно.
4. Проверка понимания учащимися нового материала. Закрепление нового материала.
Рассмотрим применение формул двойного угла для нахождения значений тригонометрических функций и преобразования тригонометрических выражений.
Решение упражнений:1. Известно, что cosx = 0,8. Найти sin2x, cos2x, tg2x, если 3𝜋/2 Вопросы учащимся: Какой четверти принадлежит угол х? Какой знак имеет синус в этой четверти? Запишите в тетрадях основное тригонометрическое тождество Sin 2 x + cos 2 x = 1? Выразите sinx. Вычислите его значение, используя условие.
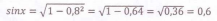
Поскольку синус в 1 четверти имеет знак «плюс», то и его значение положительно.
Как выражается tgx x через cosx и sinx? Найдите его значение самостоятельно.
- Вычислить sin50°/sin25°, используя одну из выведенных формул.
5.Обучающая самостоятельная работа.
Карточки выбирают ученики с учетом того, как они усвоили новый материал.
Проверка самостоятельной работы.
6. Домашнее задание. Подведение итогов урока.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
