Т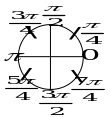 ригонометрия
ригонометрия
|
| 0 | 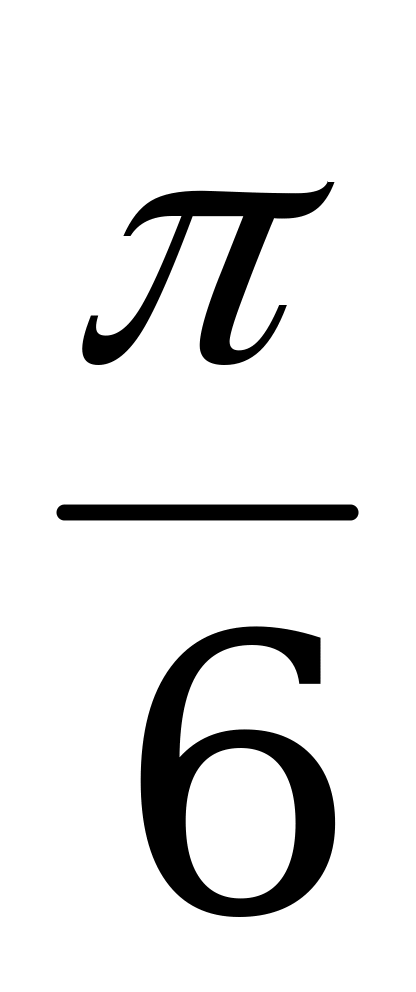
| 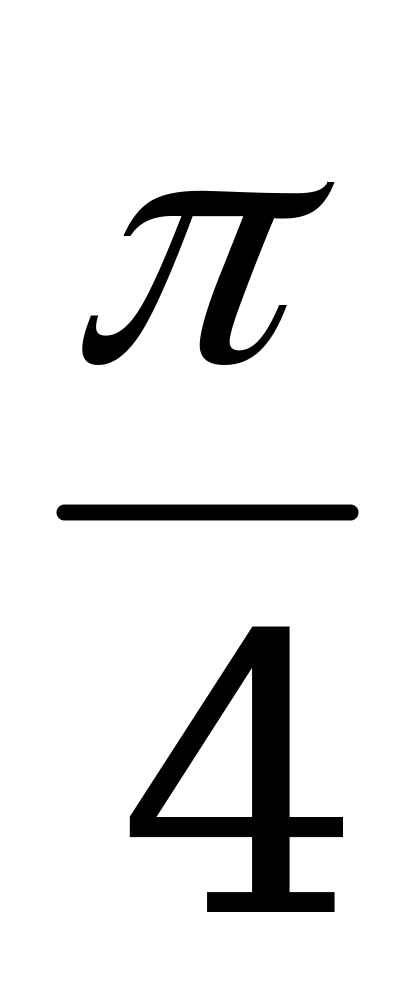
| 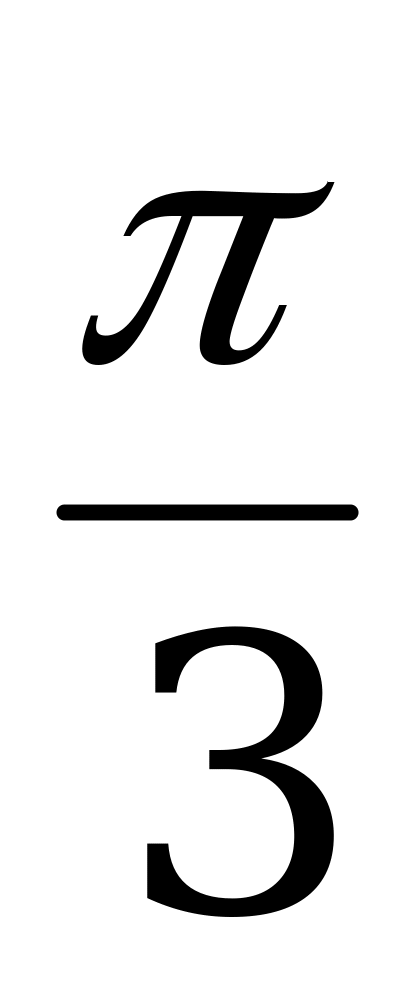
| 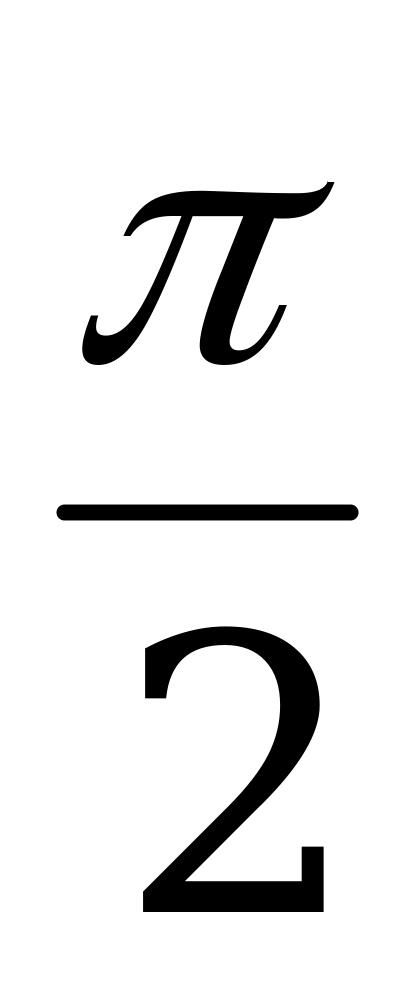 | 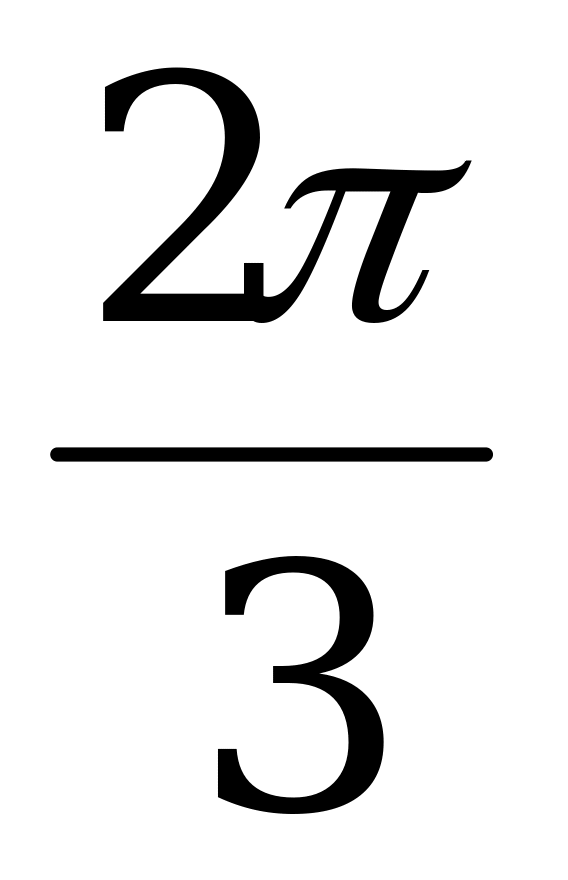
| 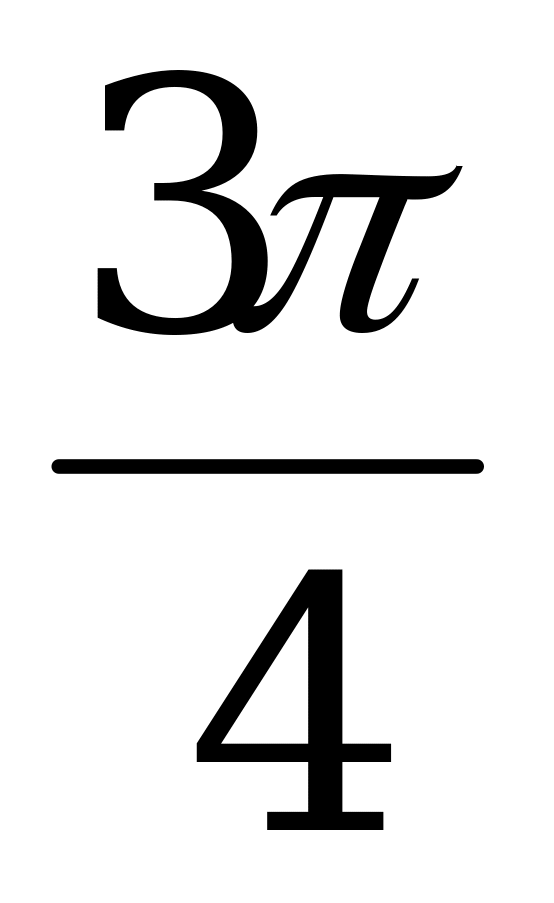
| 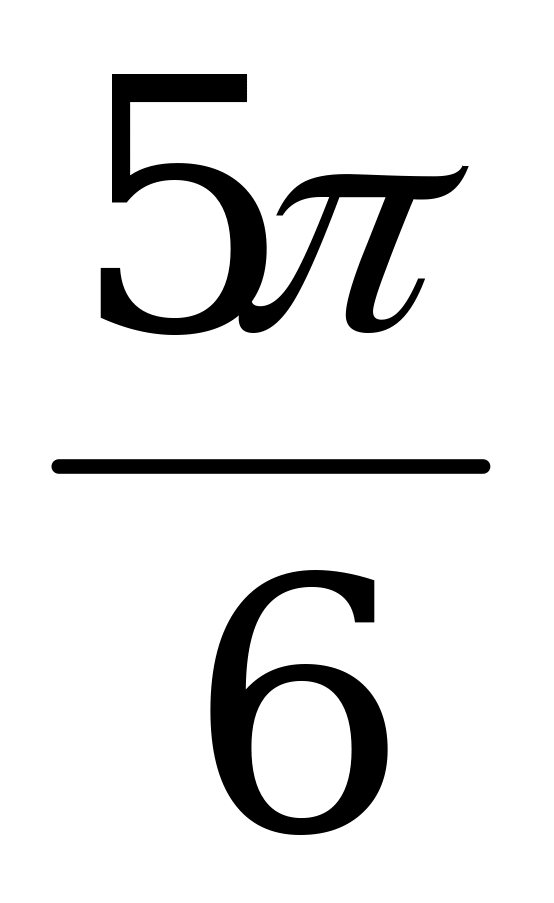
| π | 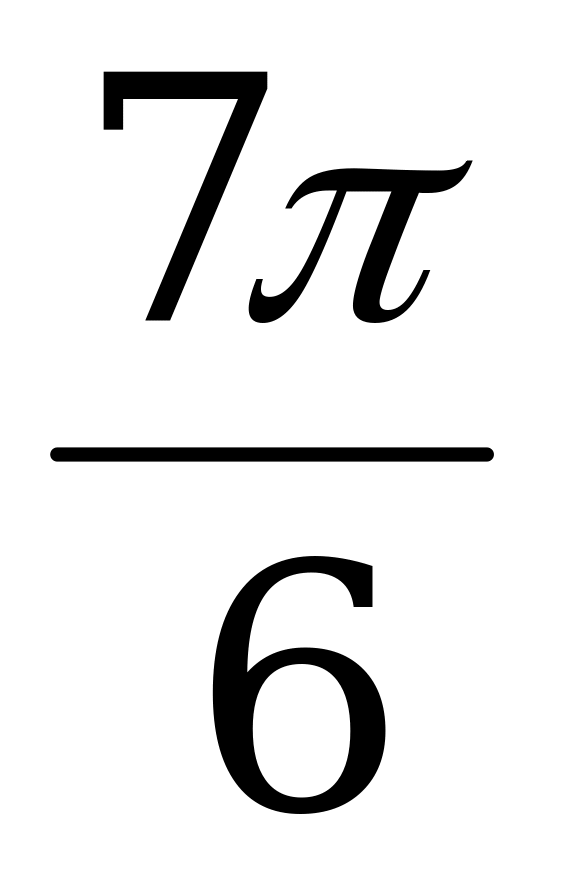
| 
| 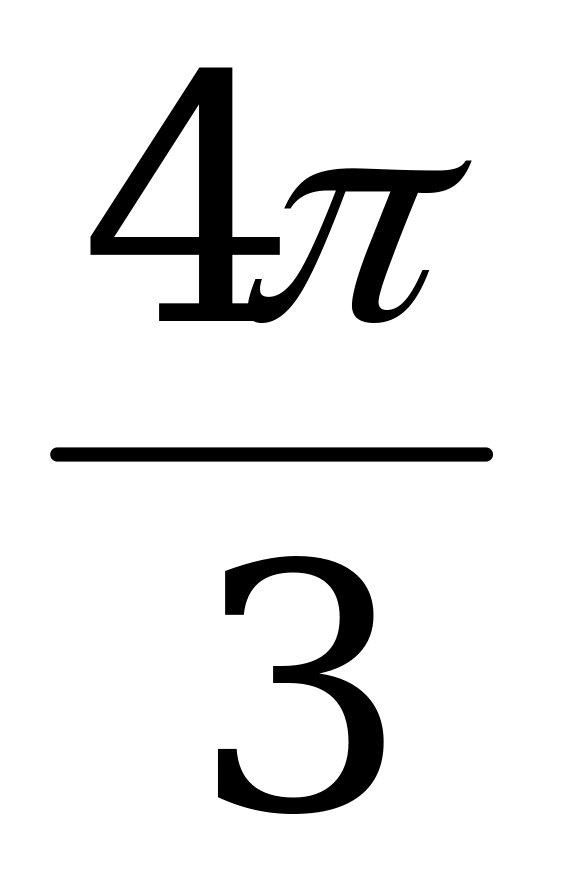
| 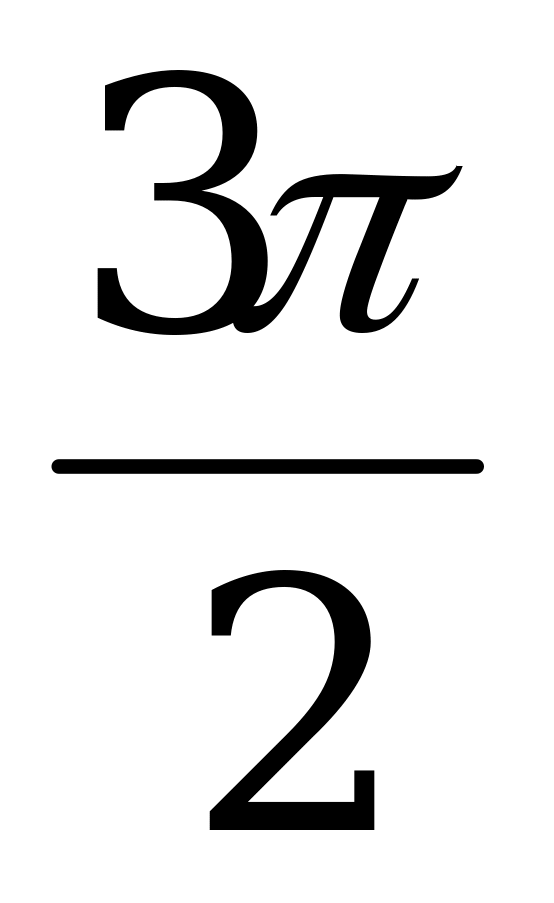
| 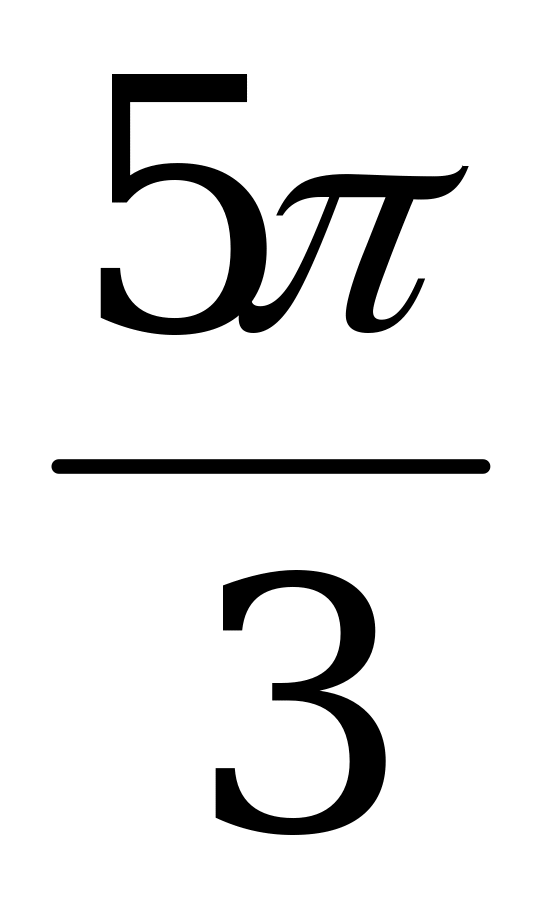
| 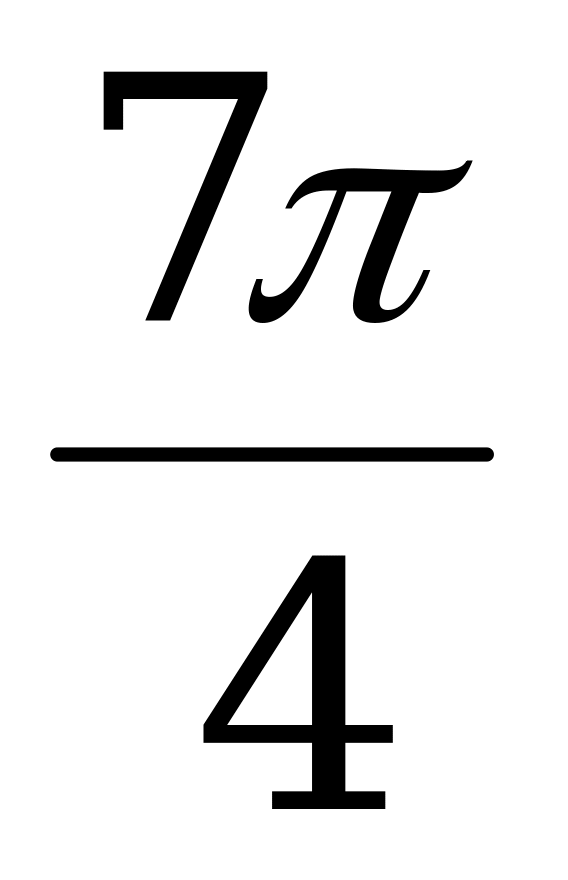
| 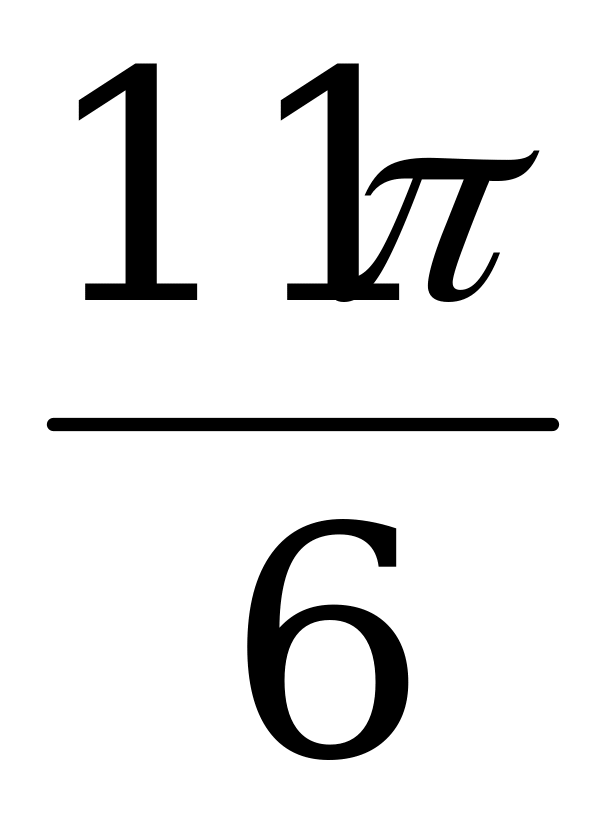
| 2 π |
| | 0 | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| sinx | 0 | 1/2 | 2/2 | Ö3/2 | 1 | Ö3/2 | Ö2/2 | 1/2 | 0 | -1/2 | -Ö2/2 | -Ö3/2 | -1 | -Ö3/2 | -Ö2/2 | -1/2 | 0 |
| cosx | 1 | Ö3/2 | Ö2/2 | 1/2 | 0 | -1/2 | -Ö2/2 | -Ö3/2 | -1 | -Ö3/2 | -Ö2/2 | -1/2 | 0 | 1/2 | Ö2/2 | Ö3/2 | 1 |
| tg x | 0 | 1/Ö3 | 1 | Ö3 |
| -Ö3 | -1 | -1/Ö3 | 0 | 1/Ö3 | 1 | Ö3 |
| -Ö3 | -1 | -1/Ö3 | 0 |
| ctg x |
| Ö3 | 1 | 1/Ö3 | 0 | -1/Ö3 | -1 | -Ö3 |
| Ö3 | 1 | 1/3 | 0 | -1/Ö3 | -1 | -Ö3 |
|
1


 . sin2x + cos2x = 1 6. sin 2x = 2sin x*cos x 11. cos2x =
. sin2x + cos2x = 1 6. sin 2x = 2sin x*cos x 11. cos2x = 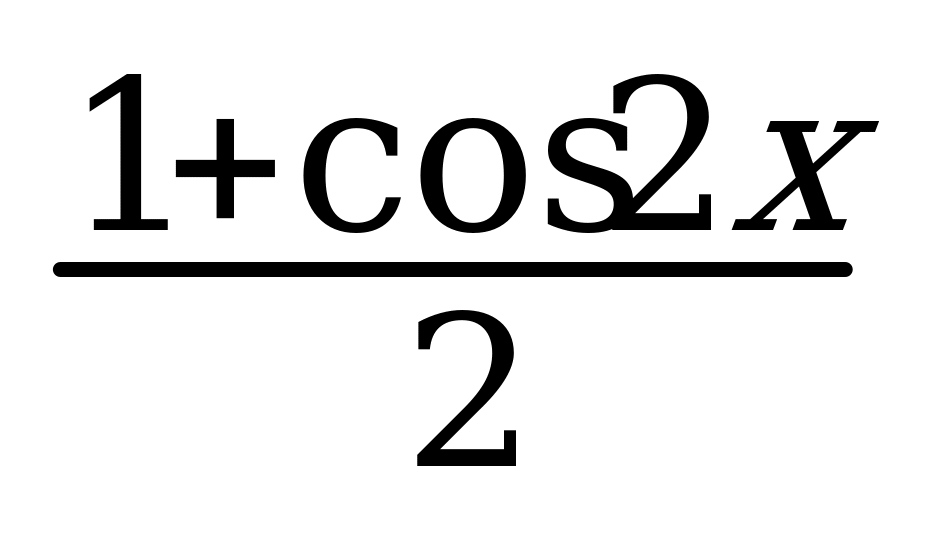 22.sinx ± siny =
22.sinx ± siny = 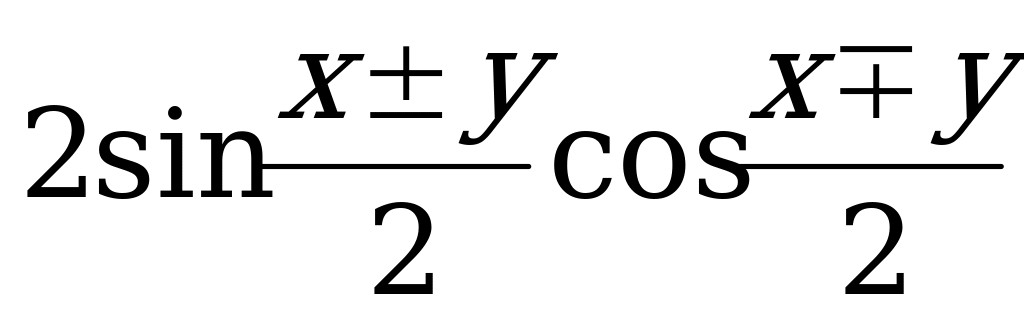 26.
26. 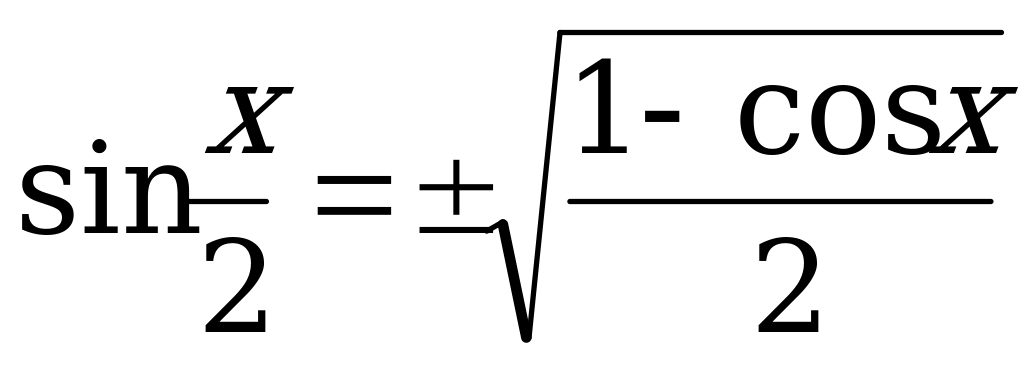
2. tg x*ctg x = 1 7. cos 2x = cos2x – sin2x 12. sin2x = 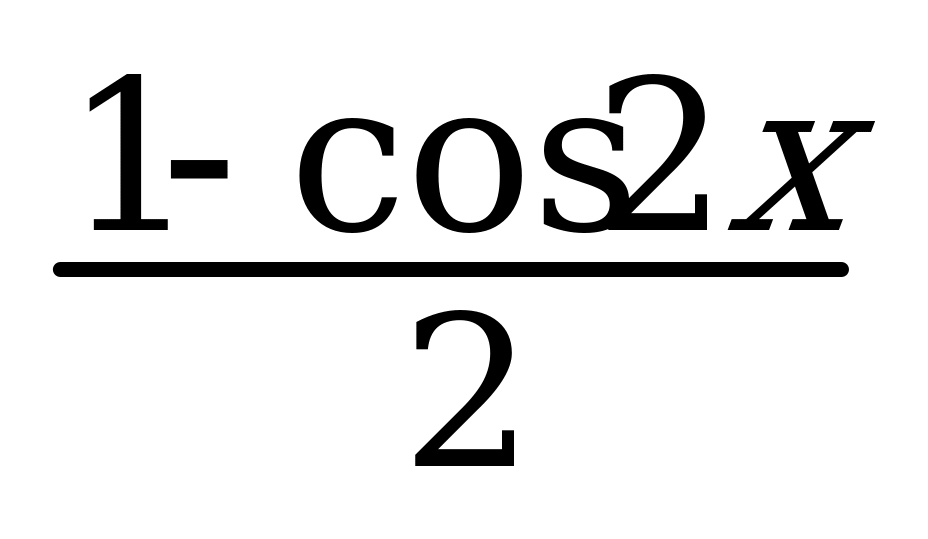 23. cos x + cos y =
23. cos x + cos y = 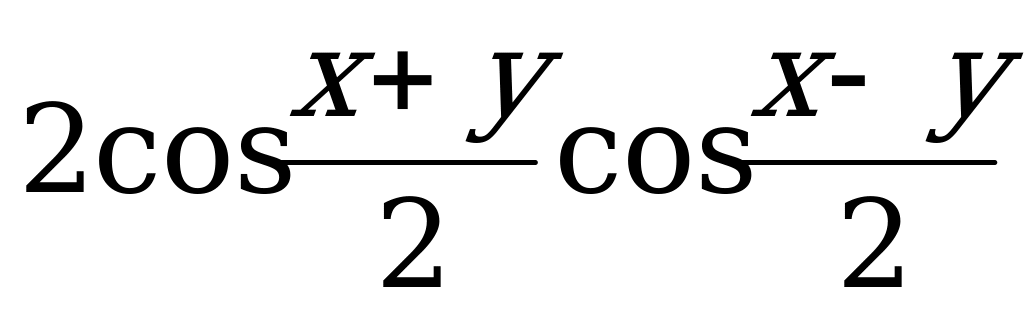 27.
27. 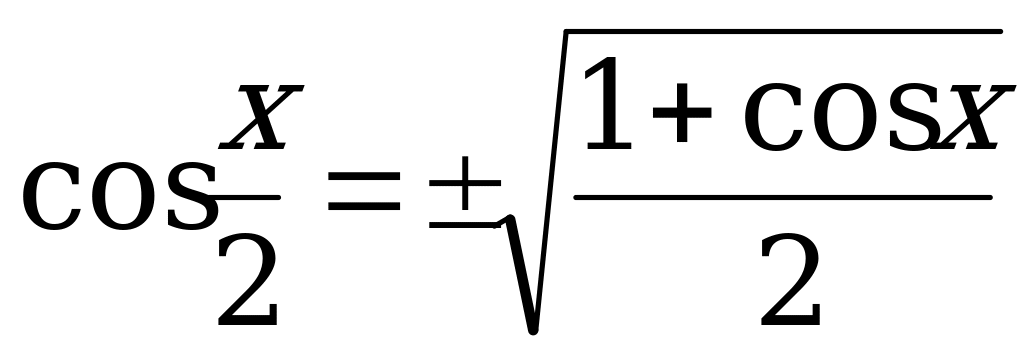
3. 1 + tg2x = 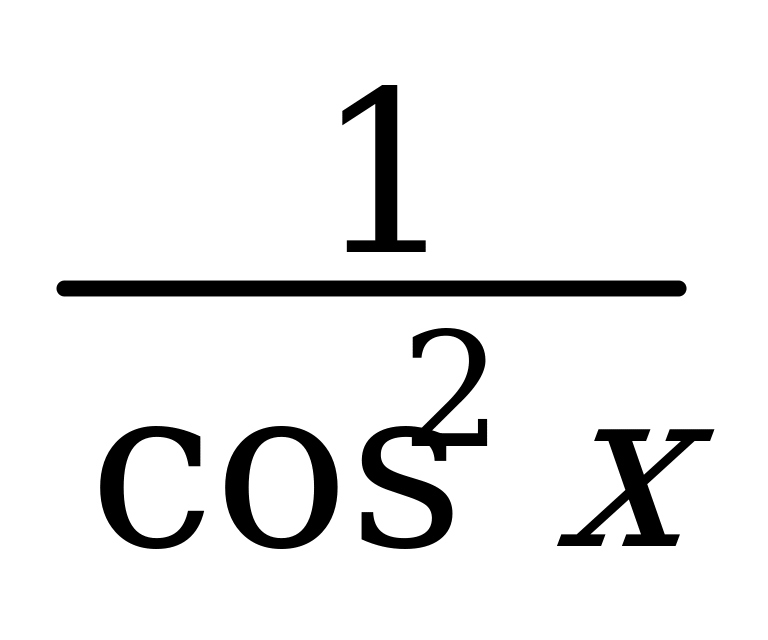 8. cos 2x = 2cos2 - 1 13.cos3x =
8. cos 2x = 2cos2 - 1 13.cos3x =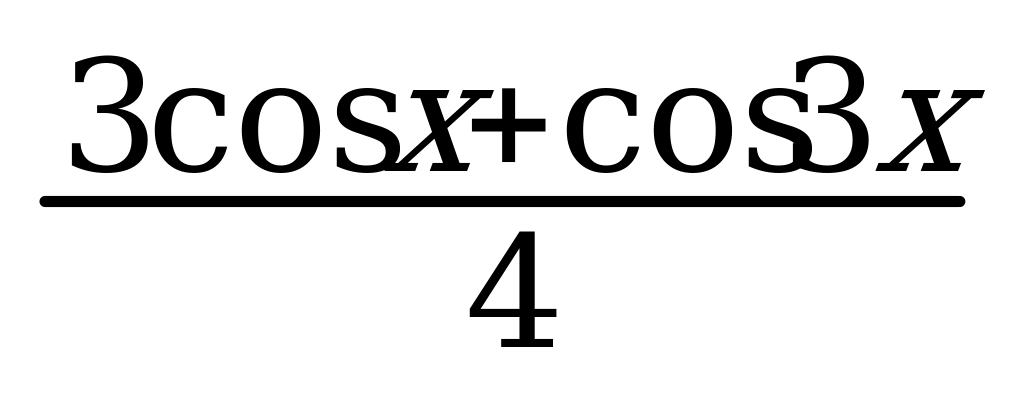 24. cos x - cos y =
24. cos x - cos y = 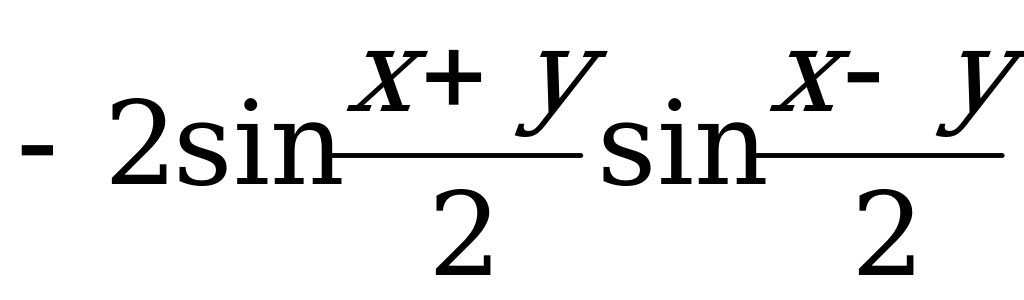 28.
28. 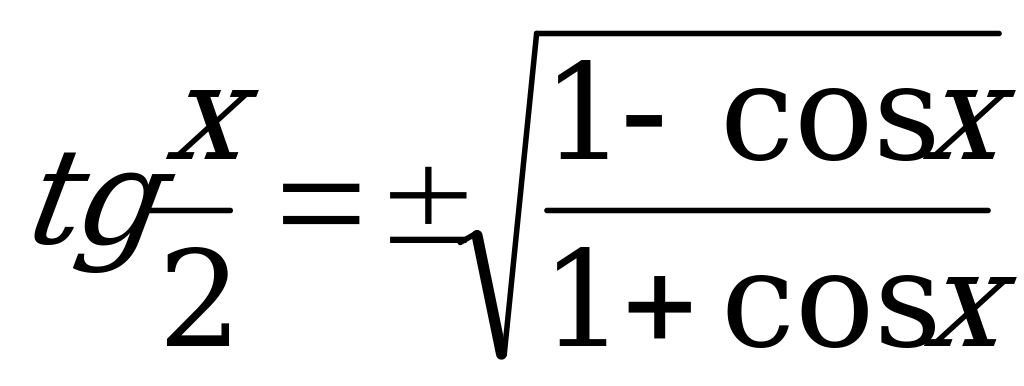
4. 1 + ctg2x = 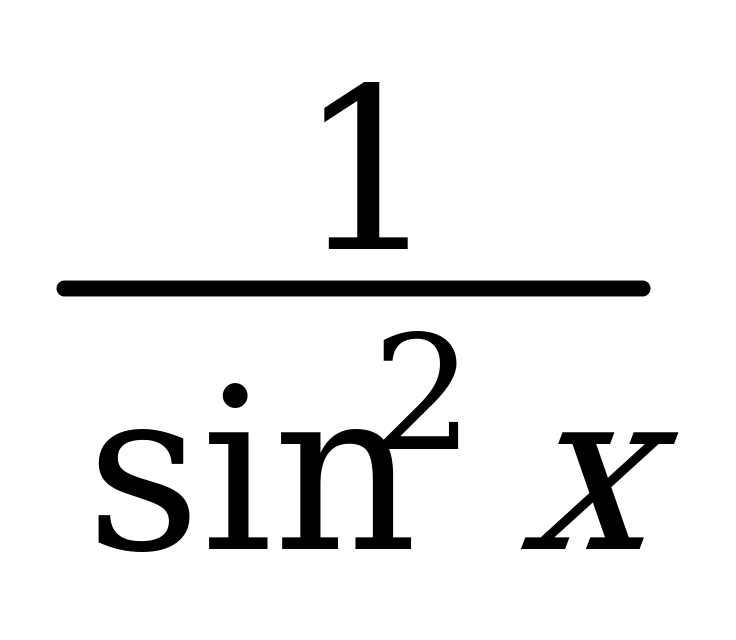 9. cos 2x = 1 – sin2x 14. sin3x =
9. cos 2x = 1 – sin2x 14. sin3x =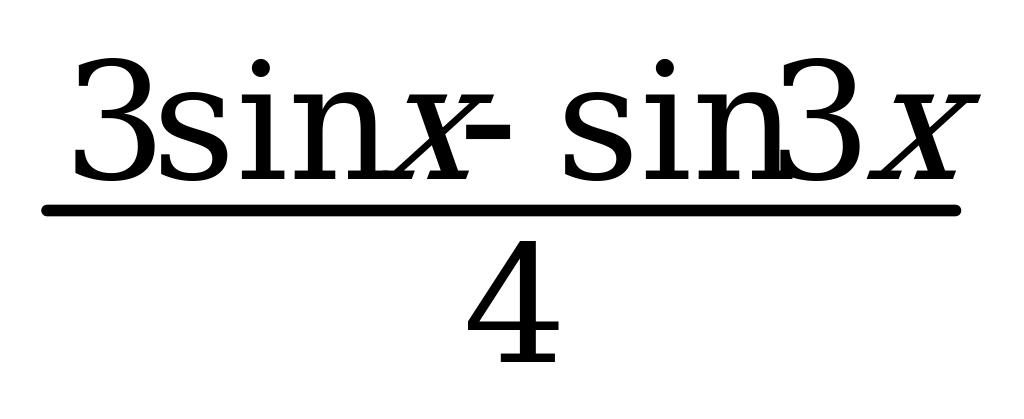 25. tgx tgy =
25. tgx tgy = 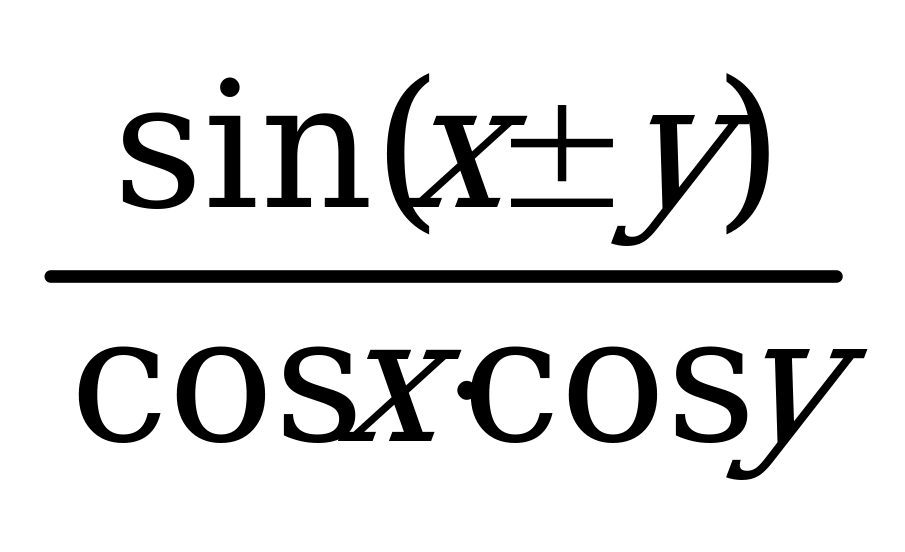
5

 . tg x + ctg x =
. tg x + ctg x = 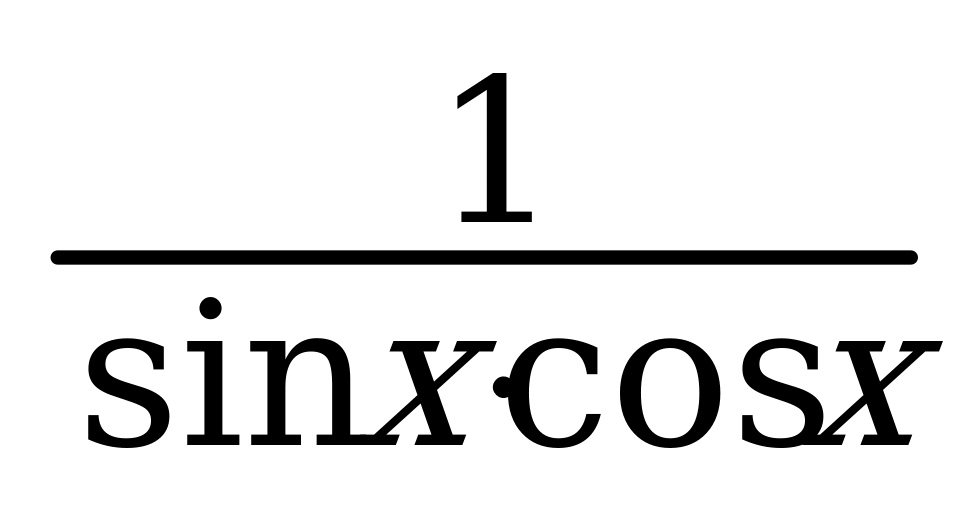 10. tg 2x =
10. tg 2x = 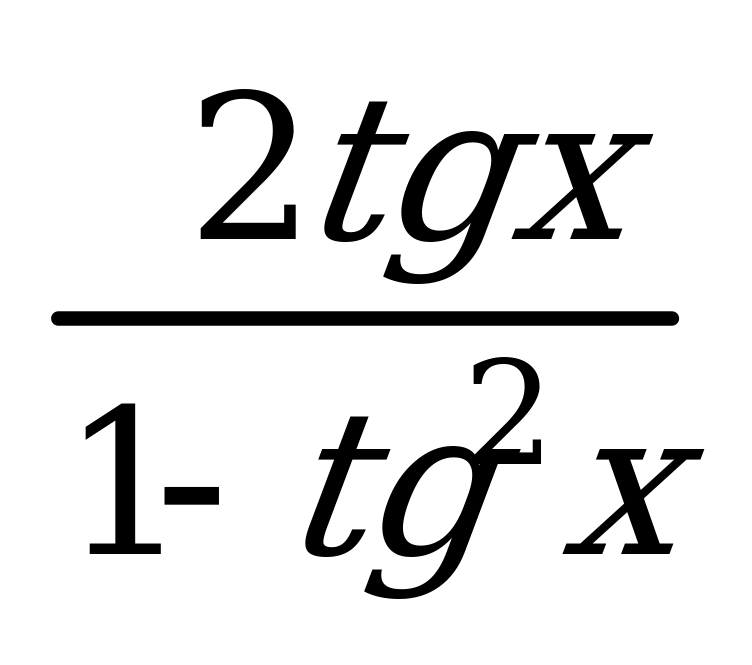 29. sin 3x = 3 sin x – 4 sin3x 30. cos 3x = 4 cos3x – 3 cos x
29. sin 3x = 3 sin x – 4 sin3x 30. cos 3x = 4 cos3x – 3 cos x
15. sin(x ± y) = sin x*cos y ± cos x *siny 19. sinx* siny =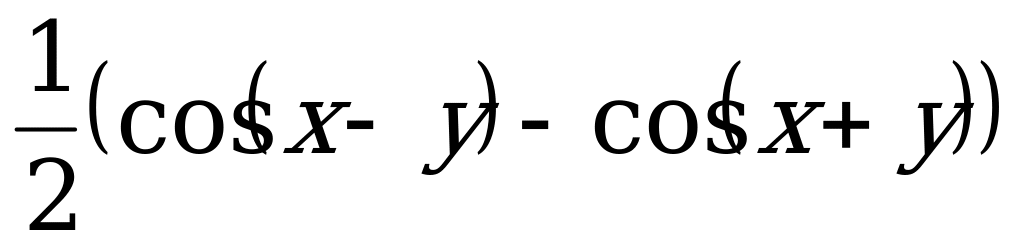 31.
31. 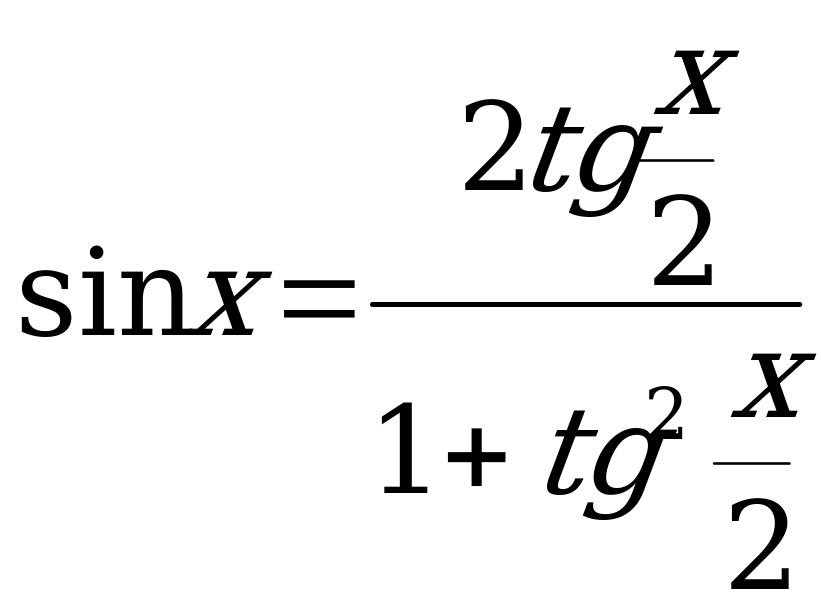 32.
32. 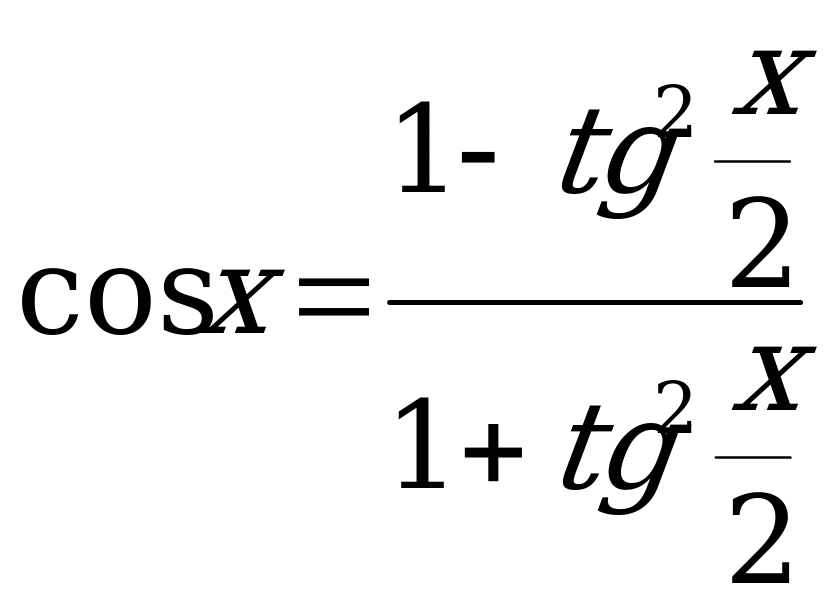

 16. cos(x + y) = cos x*cosy - sinx*siny 20. cosx*cosy =
16. cos(x + y) = cos x*cosy - sinx*siny 20. cosx*cosy = 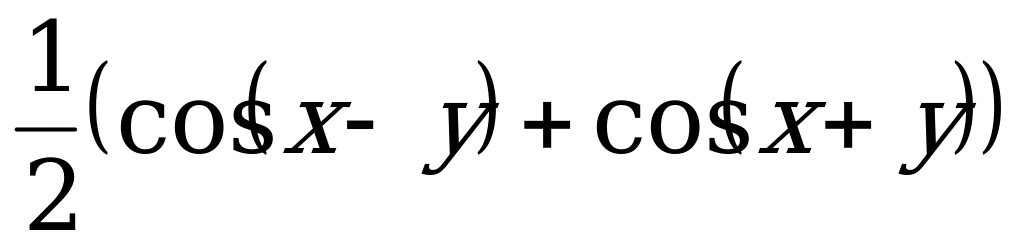 1. sin x = 0, x = πn. 1. cos x = 0, x =
1. sin x = 0, x = πn. 1. cos x = 0, x = 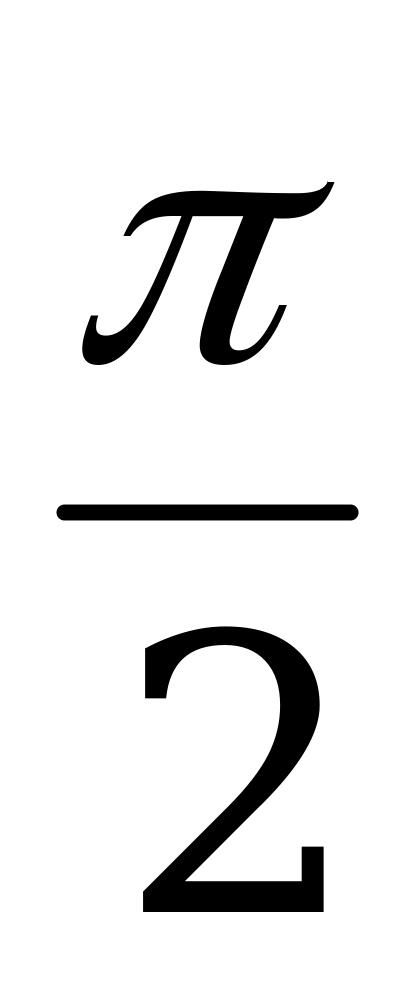 + πn.
+ πn.
17. cos(x - y) = cos x*cosy + sinx*siny 2. sin x = 1, x = 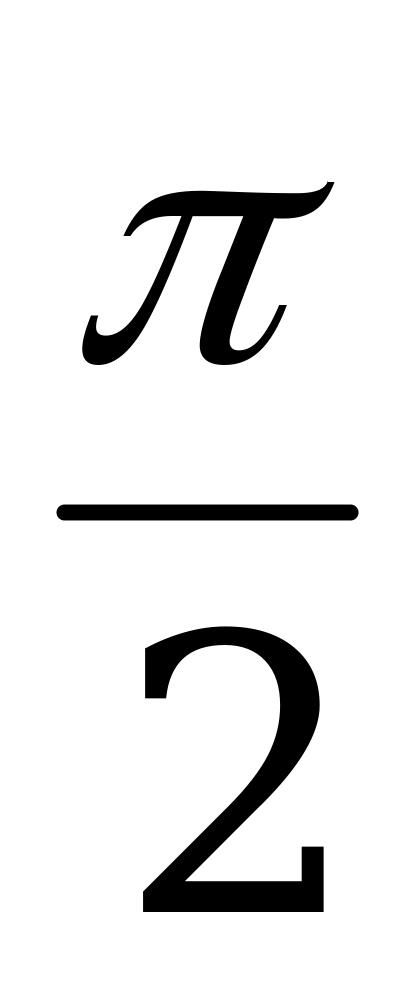 + 2 πn. 2. cos x = 1, x = 2 πn.
+ 2 πn. 2. cos x = 1, x = 2 πn.
18. tg(x ± y) = 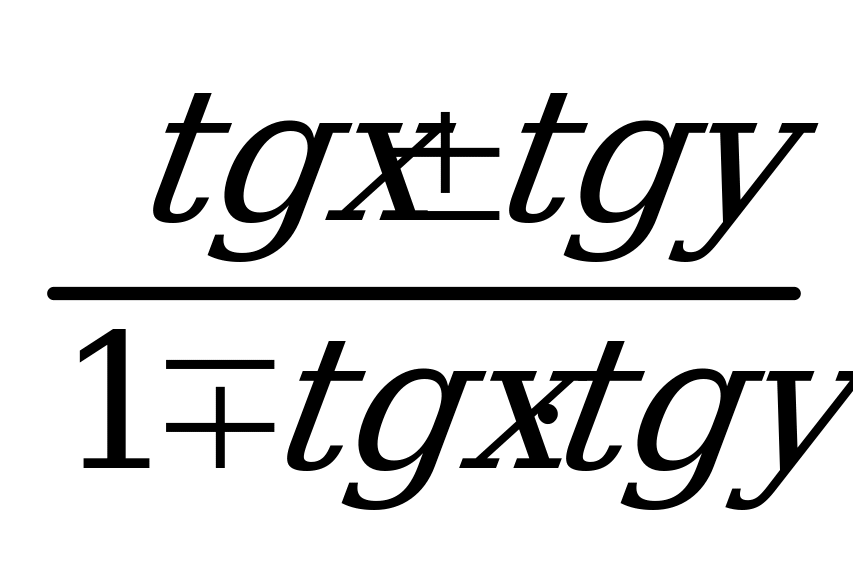 21. sinx*cosy =
21. sinx*cosy = 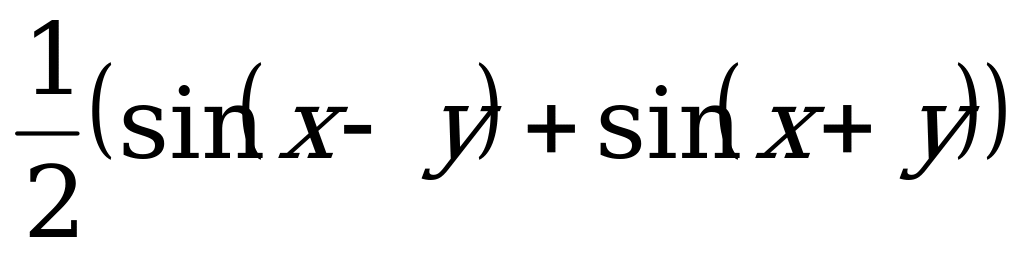 3. sin x = -1, x = -
3. sin x = -1, x = - 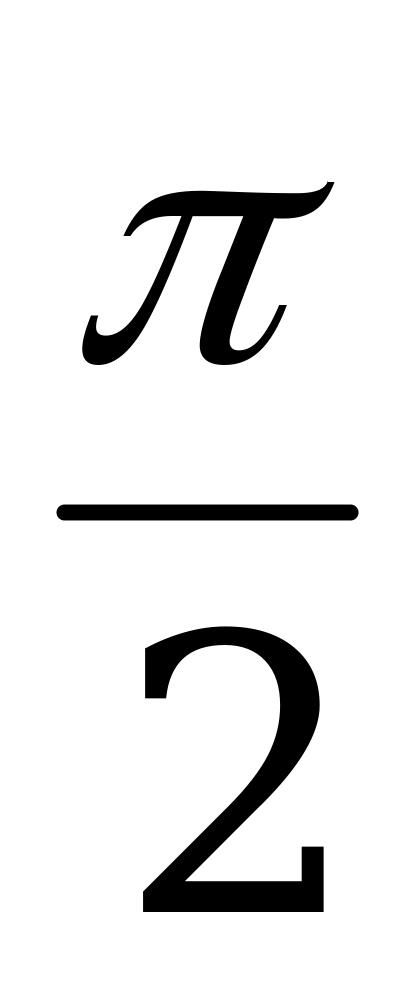 + 2 πn. 3. cos x = -1, x = π + 2 πn.
+ 2 πn. 3. cos x = -1, x = π + 2 πn.
4. sin x = a, x = (-1)narcsin a + πn 4. cos x = a, x = ± arcos a + 2 πn
К вадратное уравнение: ax2 + bx + c = 0 ax2 + bx + c = a(x – x1)(x – x2) 1. tg x = 0, x = πn. 2. tg x = ± 1, x = ±
вадратное уравнение: ax2 + bx + c = 0 ax2 + bx + c = a(x – x1)(x – x2) 1. tg x = 0, x = πn. 2. tg x = ± 1, x = ± 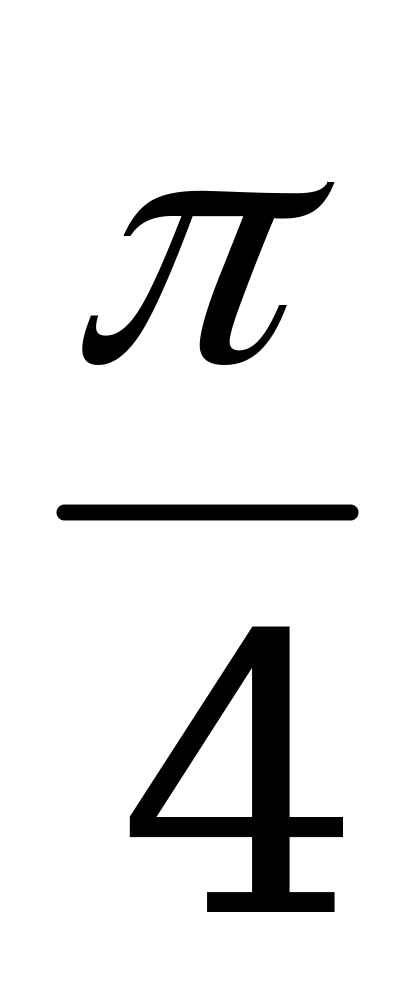 + πn.
+ πn.
D = 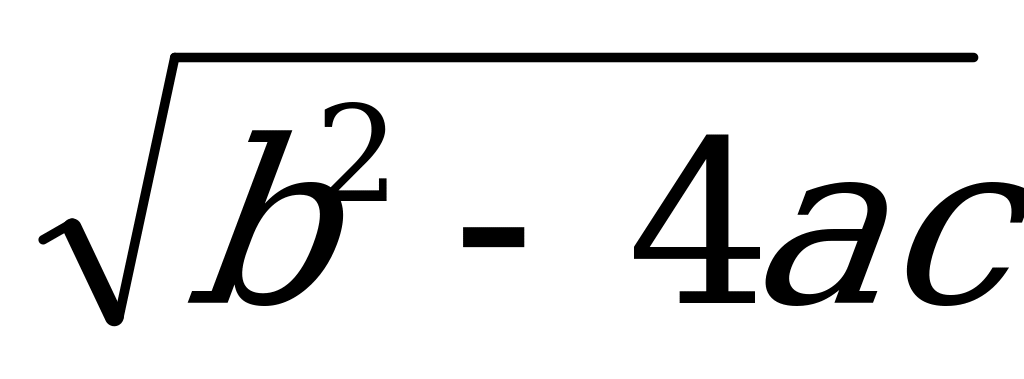 X1,2 =
X1,2 = 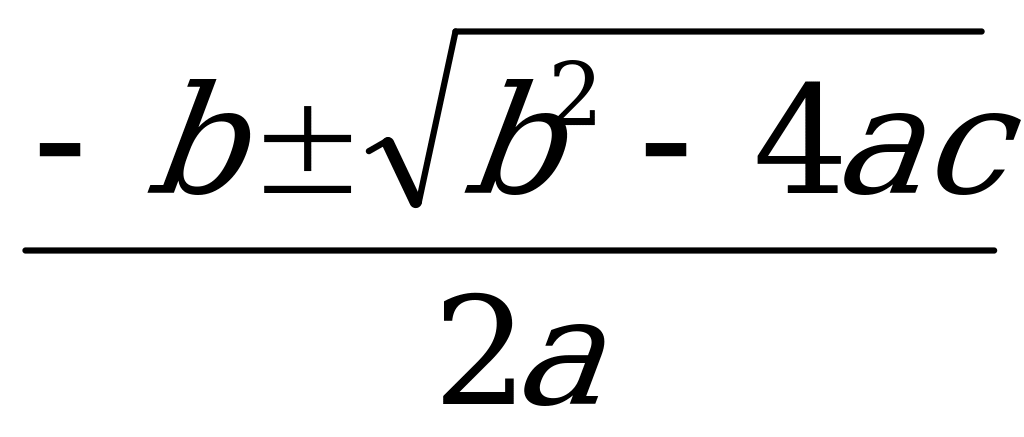 3. tg x = a, x = arctg a + πn.
3. tg x = a, x = arctg a + πn.
Теорема Виета: x2 + px + q = 0; x1 + x2 = - p; x1 . x2 = q.

 Правила дифференцирования Правила интегрирования Логарифмы
Правила дифференцирования Правила интегрирования Логарифмы
(u + v)/ = u / + v / (ku)/ = ku/ 1. 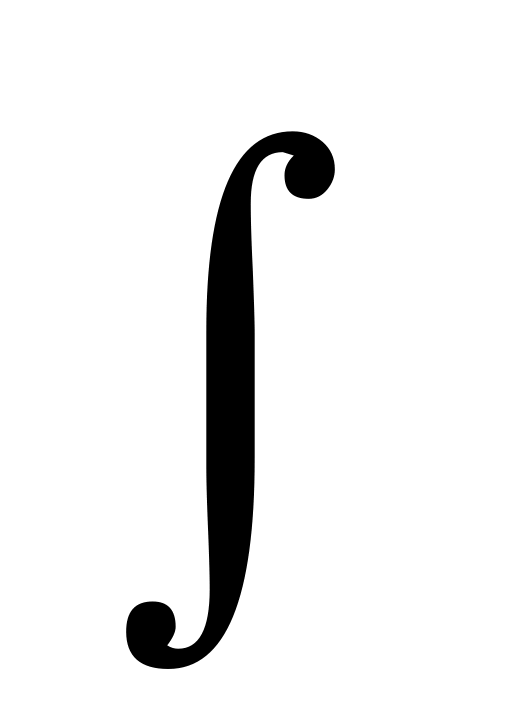 dx = x 8. ò
dx = x 8. ò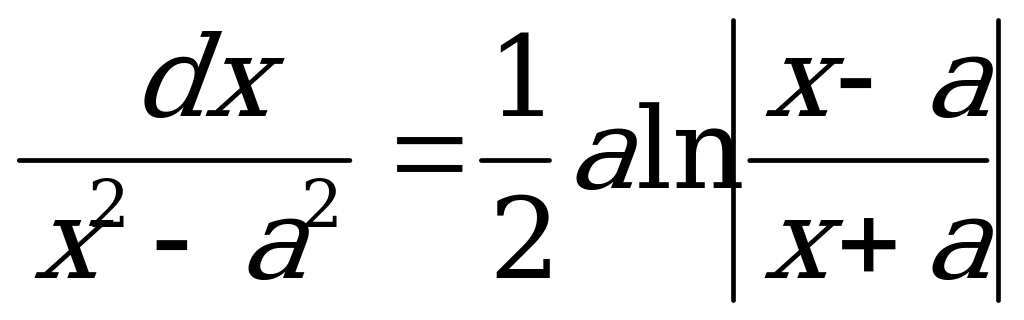 1. alogab = b 2. loga a = 1, a 1, a 0
1. alogab = b 2. loga a = 1, a 1, a 0
(uv)/ = u /v + uv / 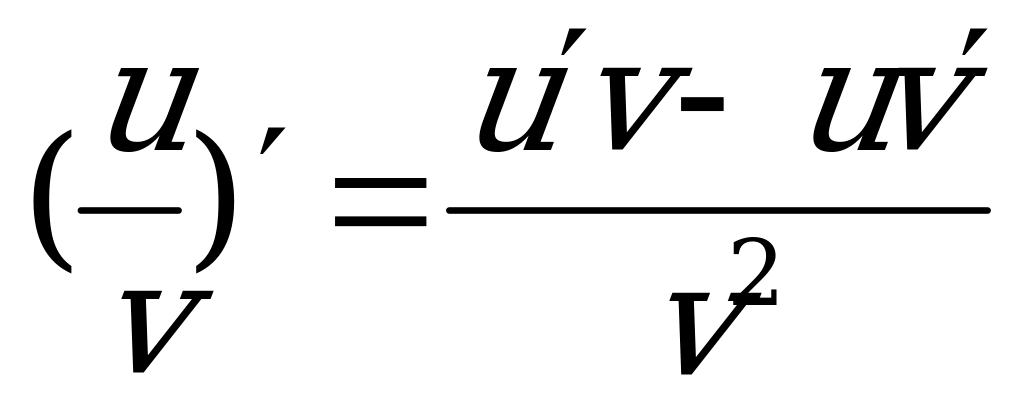 2.
2. 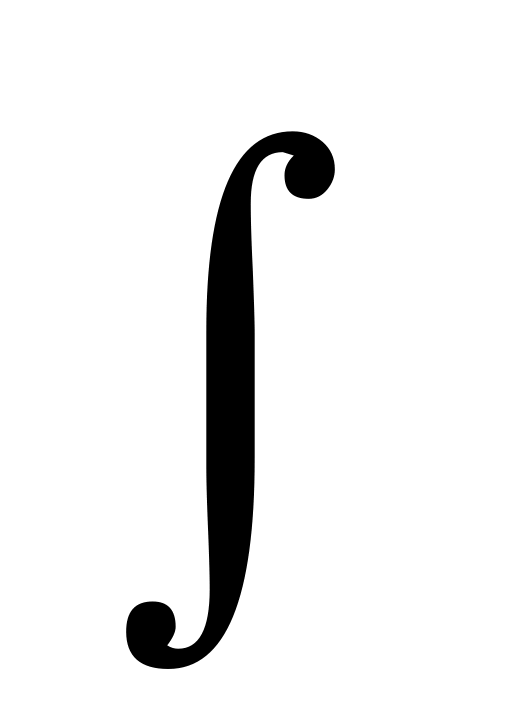 xndx =
xndx = 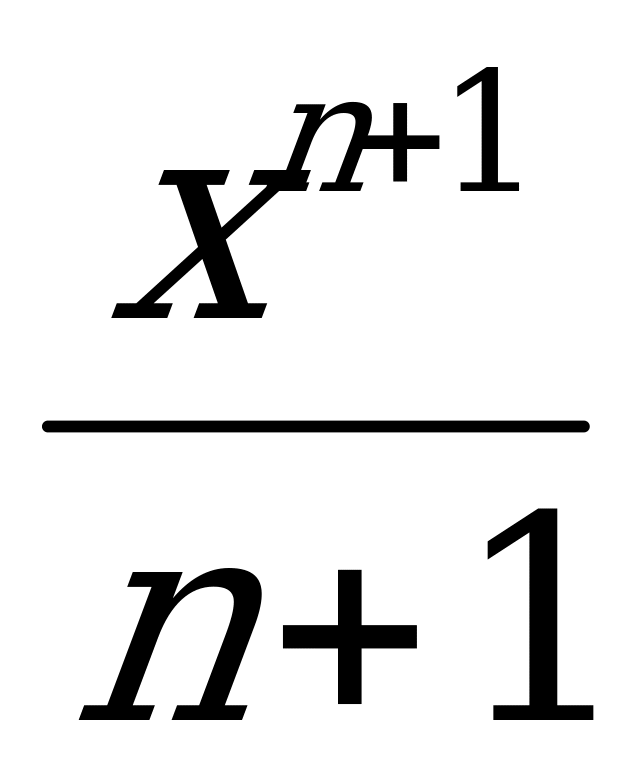 9. ò
9. ò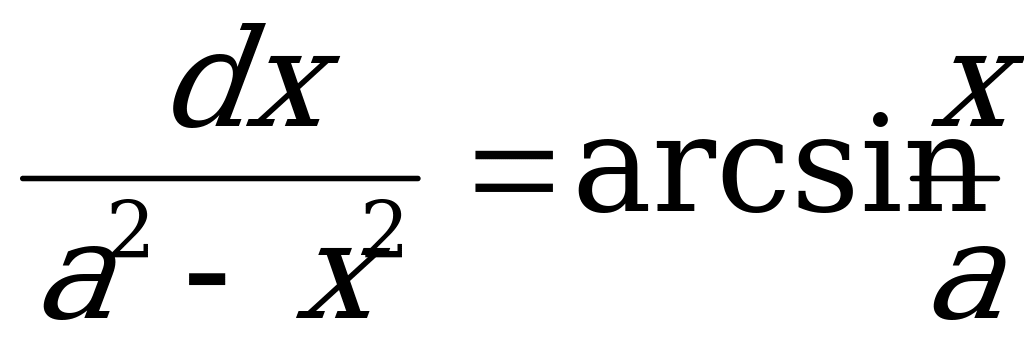 3. loga 1 = 0 4. logabc = loga b + logac
3. loga 1 = 0 4. logabc = loga b + logac
(f(kx + m))/ = kf /(kx + m) 3. 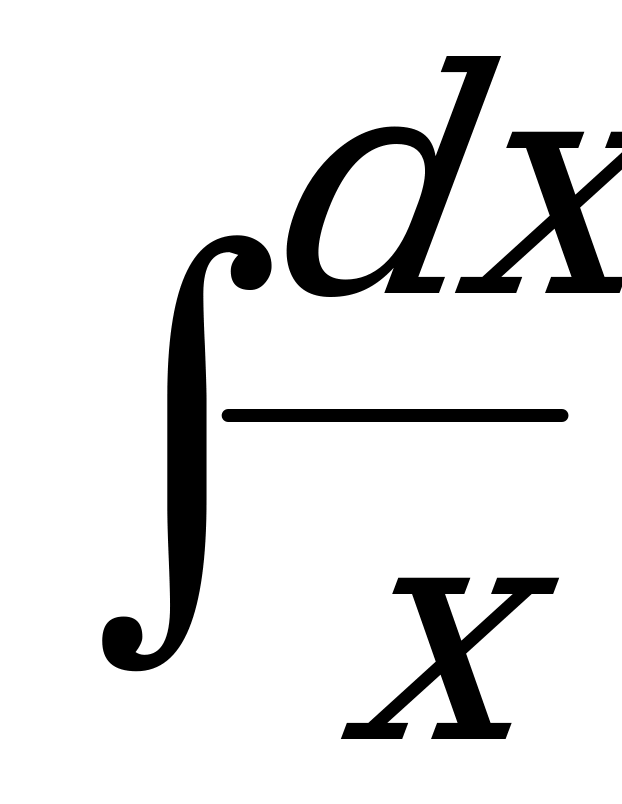 = ln | x | 10. ò
= ln | x | 10. ò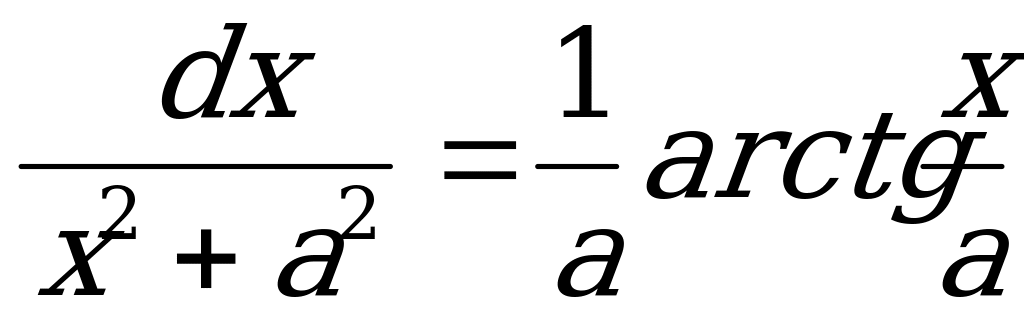 5. loga
5. loga 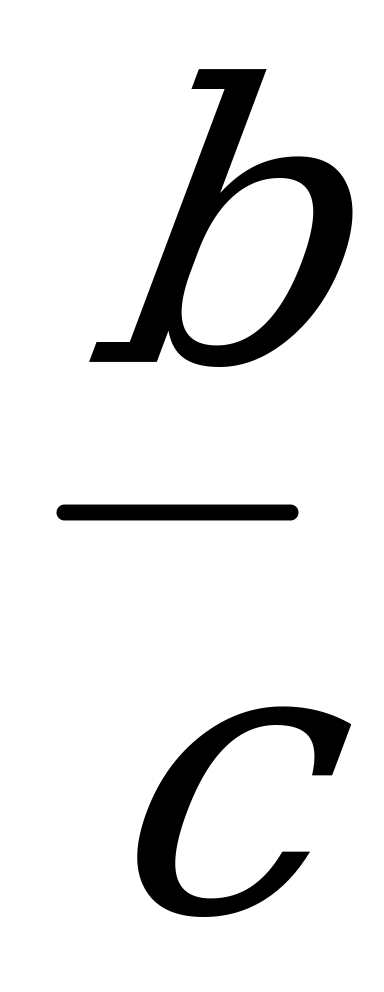 = logab – loga c
= logab – loga c
1. C = 0 2. (kx + b)= k 3. (ex)¢ = ex 4. 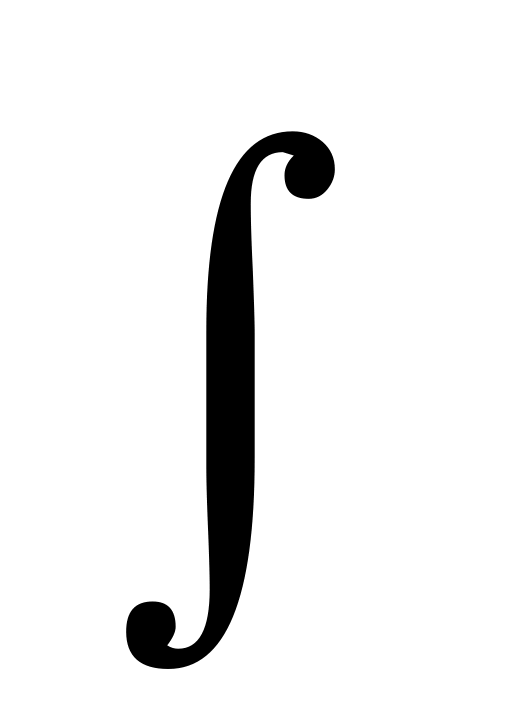 ax dx =
ax dx = 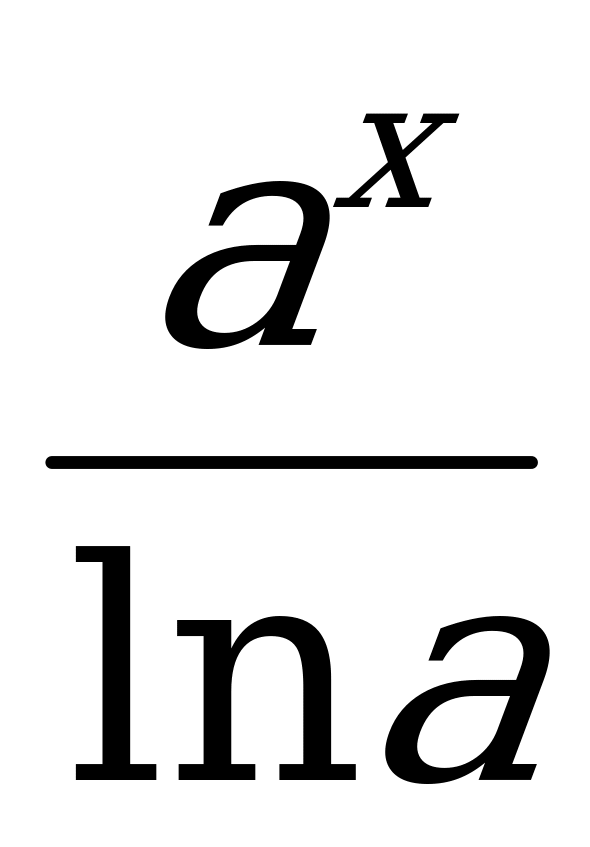 11. ò
11. ò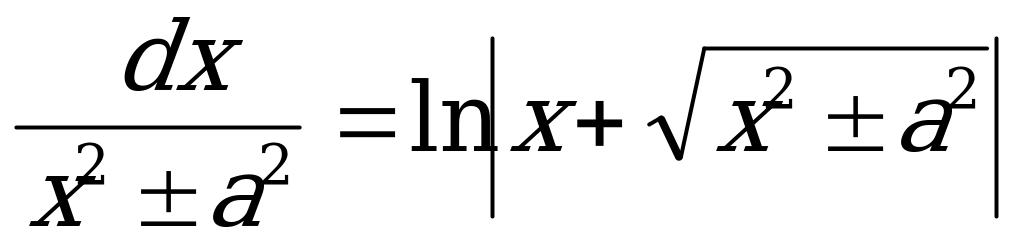 6. loga bp = p logab 7. logab =
6. loga bp = p logab 7. logab =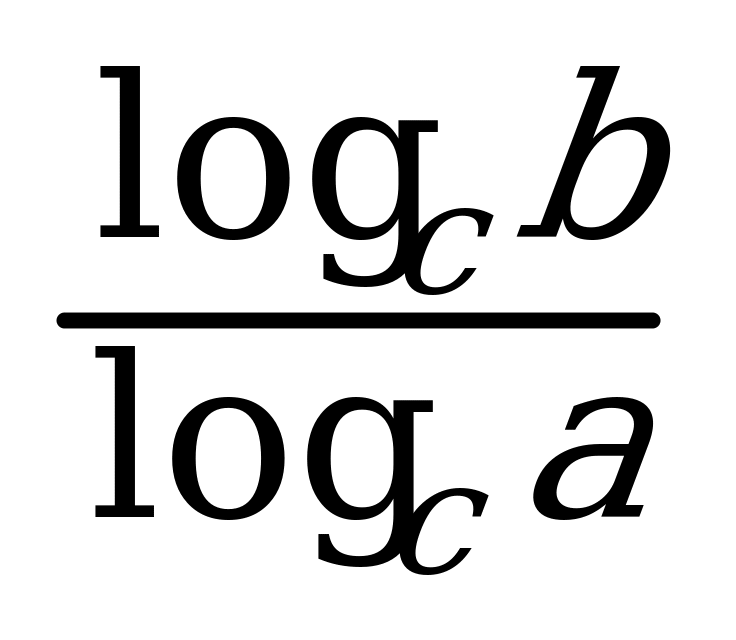

4. (xn)¢ = nxn - 1 5. (ax)¢ = ax ln a 5. ò 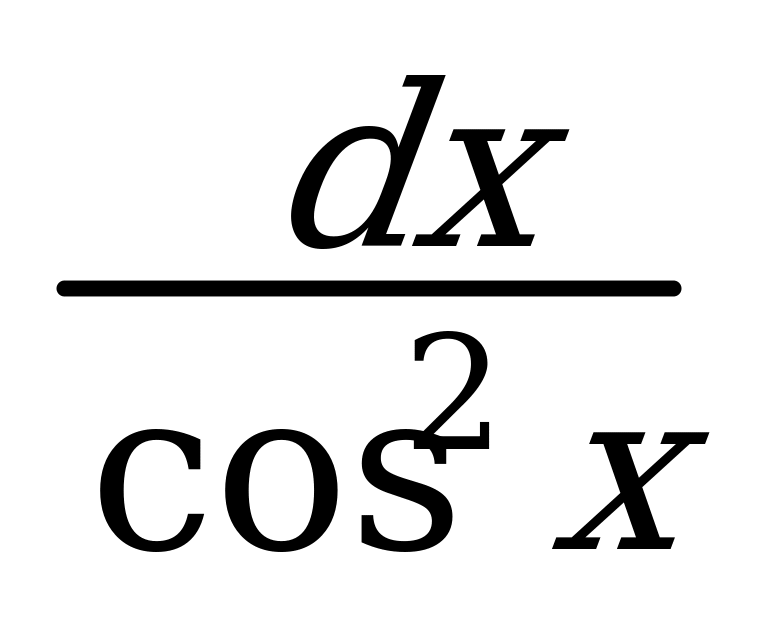 = tgx 12.
= tgx 12. 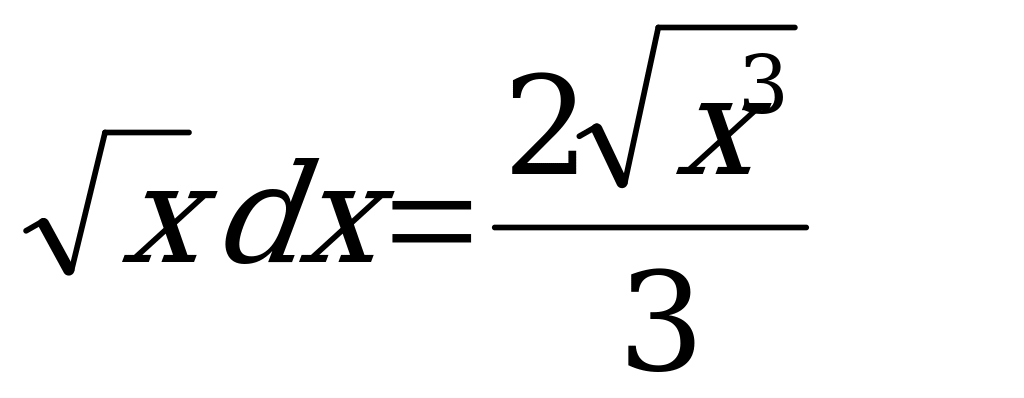 8. loga b =
8. loga b = 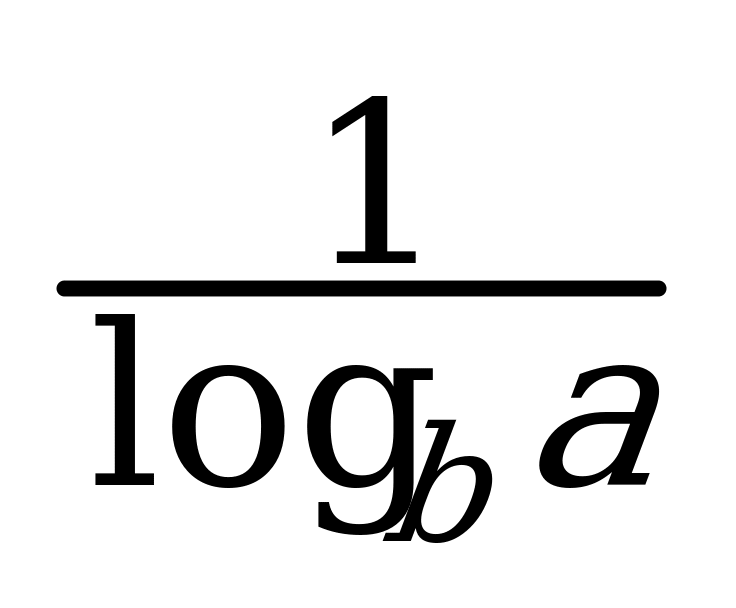 9.
9. 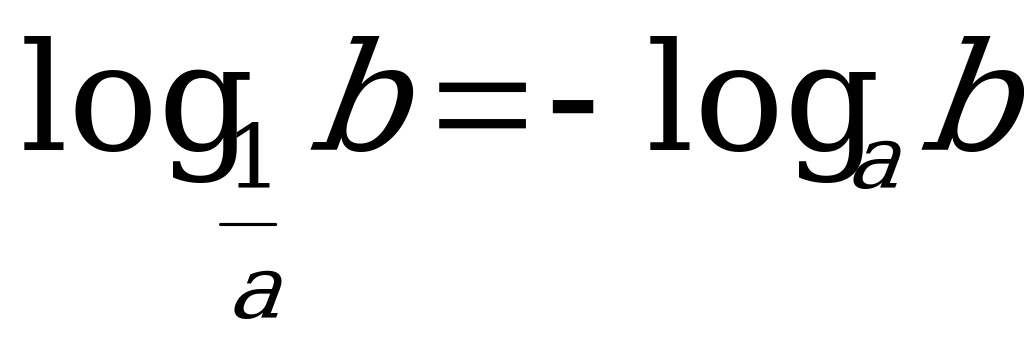
6. (sin x)¢ = cos x 7. (cos x)¢ = -sin x 6. ò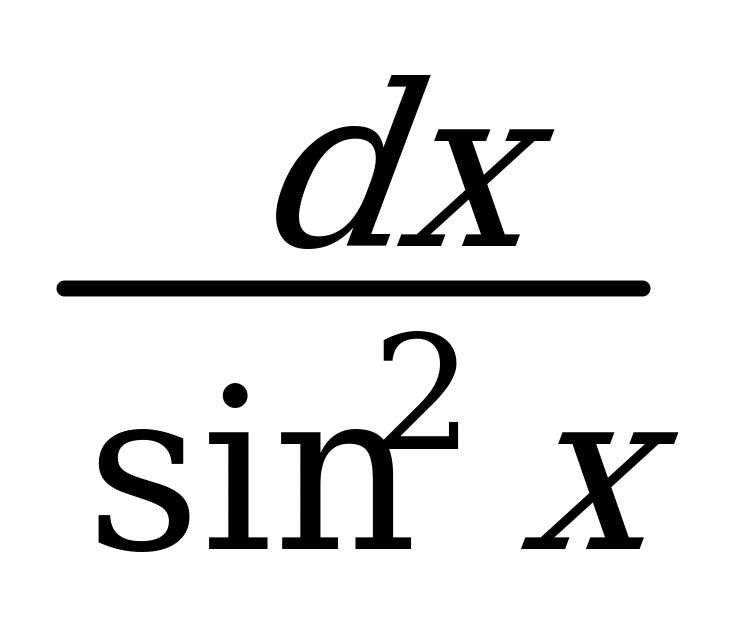 = -ctgx 13. ò cosx dx = sinx 10. logaxp = ploga | x | p – чет.
= -ctgx 13. ò cosx dx = sinx 10. logaxp = ploga | x | p – чет.
8. (tg x)¢ = 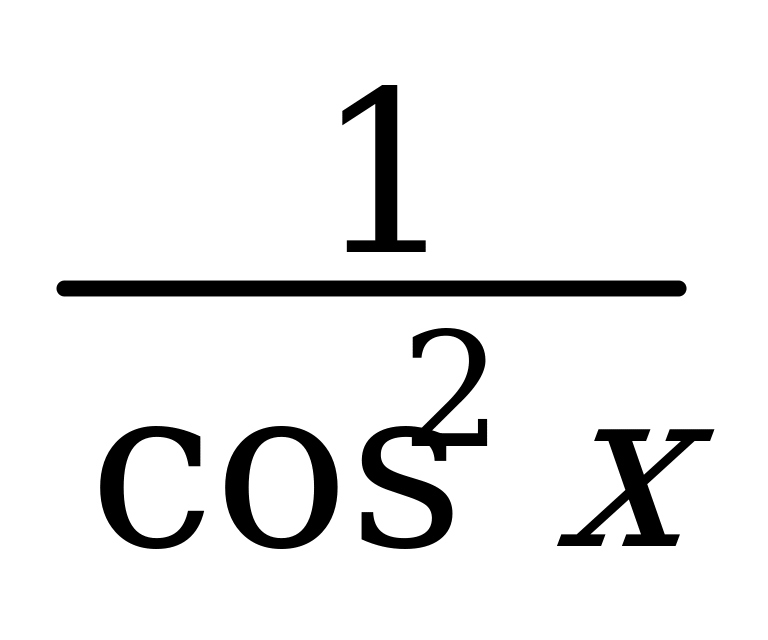 9. (ctg x)¢ = -
9. (ctg x)¢ = -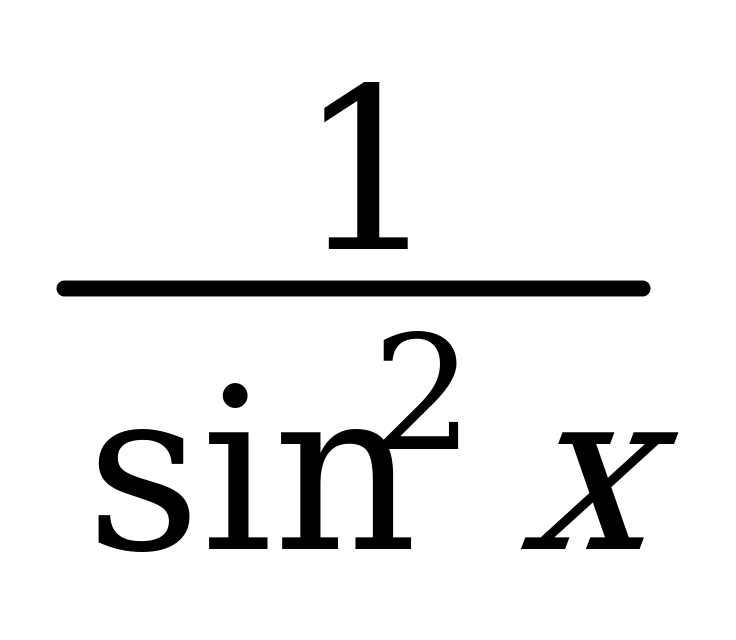 7. ò ex dx = ex 14. ò sin x dx = -cosx 11. logab = x ax = b
7. ò ex dx = ex 14. ò sin x dx = -cosx 11. logab = x ax = b
1 0.(ln x)¢ =
0.(ln x)¢ = 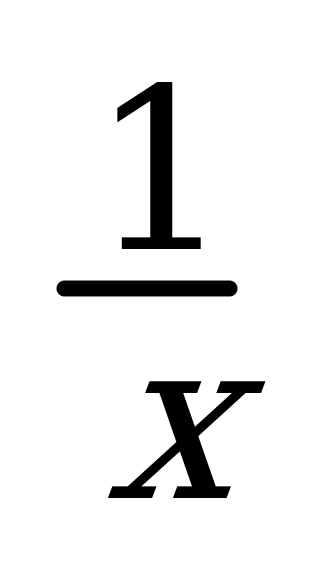 11. (logax)¢ =
11. (logax)¢ = 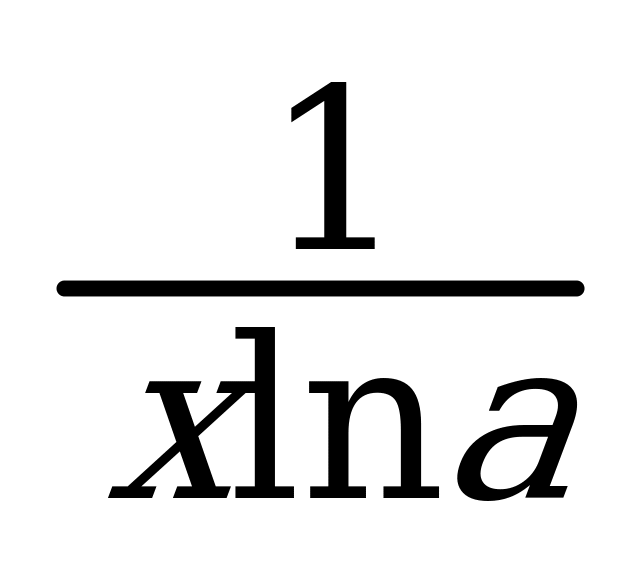 Свойства степени. ФСУ
Свойства степени. ФСУ
12. (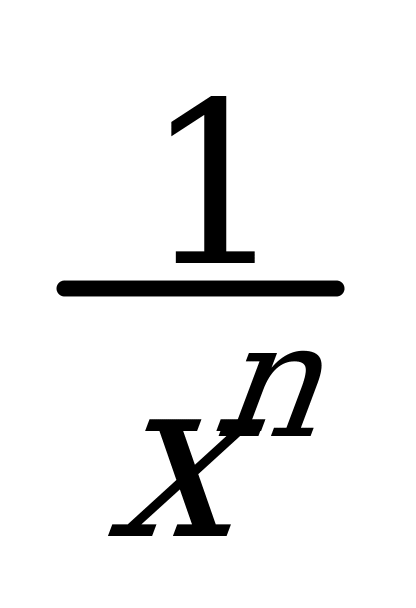 ) =
) = 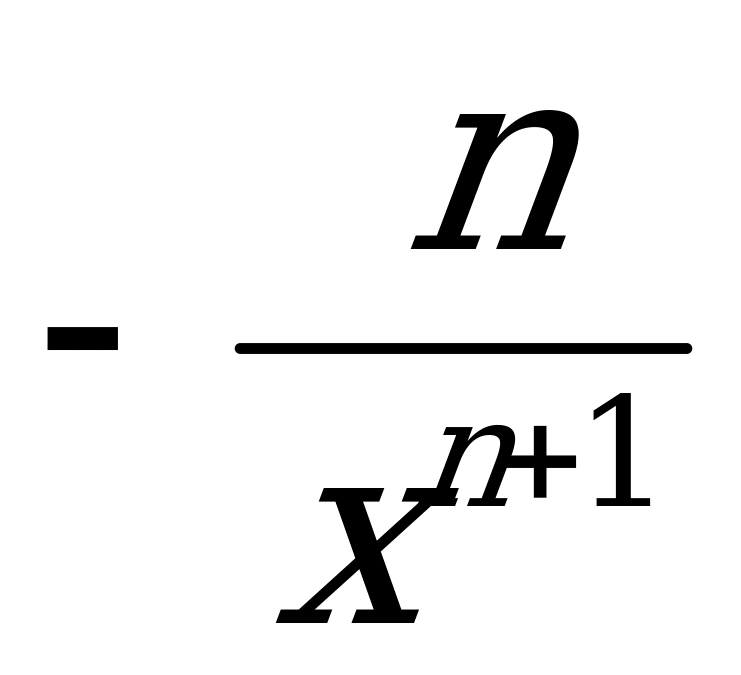 13. (arctg x)¢ =
13. (arctg x)¢ = 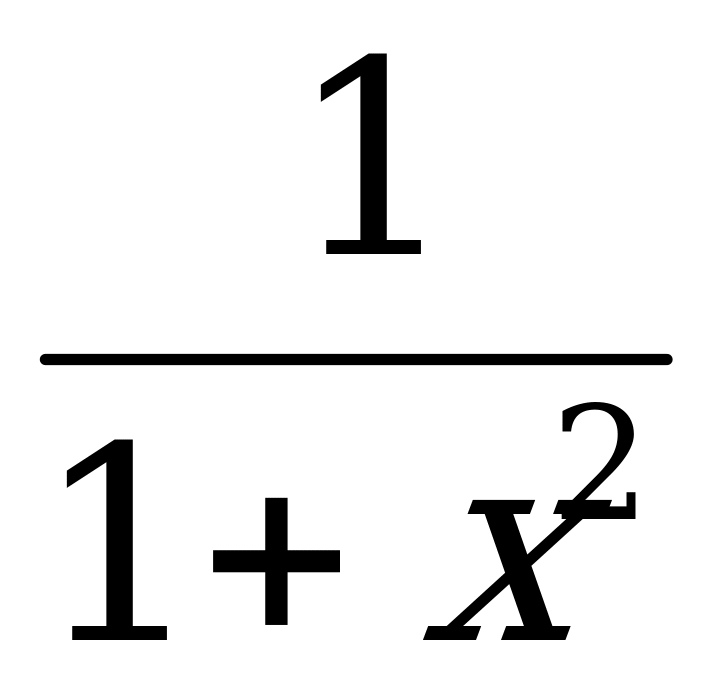 1. a0 = 1 (a0) 2. a1 = a 3. ar as = ar + s 1. a2 – b2 = (a – b)(a + b)
1. a0 = 1 (a0) 2. a1 = a 3. ar as = ar + s 1. a2 – b2 = (a – b)(a + b)
(arcsin x)¢ = 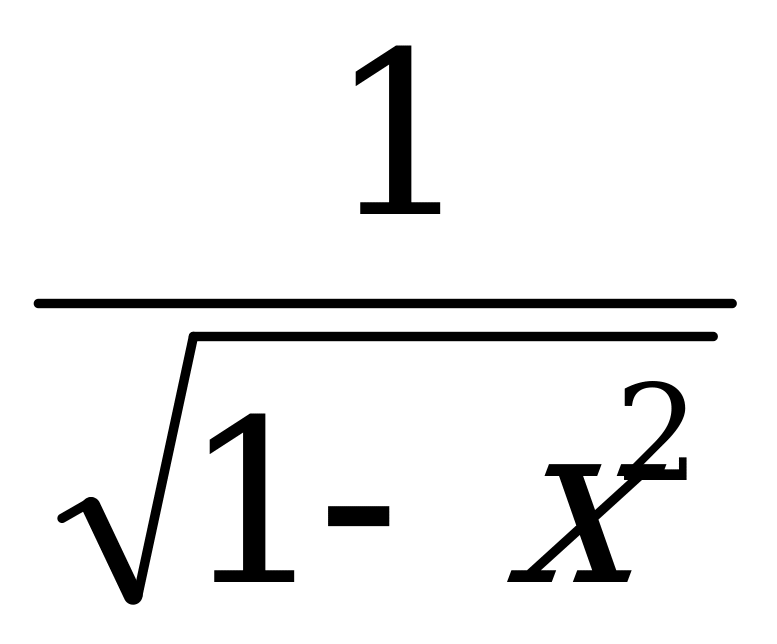 4. ar : as = ar – s 5. (ar)s = ars 6. ar br = (ab)r 2. (a + b)2 = a2 + 2ab + b2
4. ar : as = ar – s 5. (ar)s = ars 6. ar br = (ab)r 2. (a + b)2 = a2 + 2ab + b2
(arccos x)¢ = -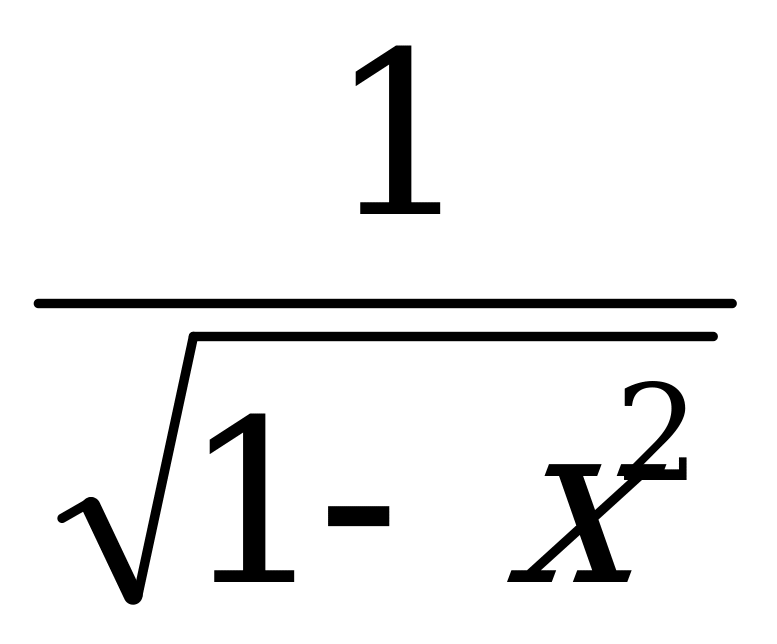 7.
7. 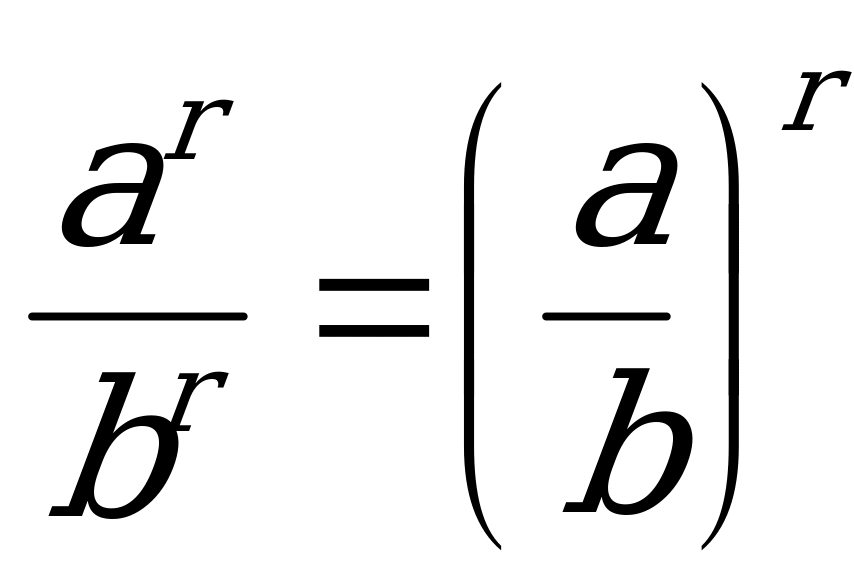 8. a-r =
8. a-r = 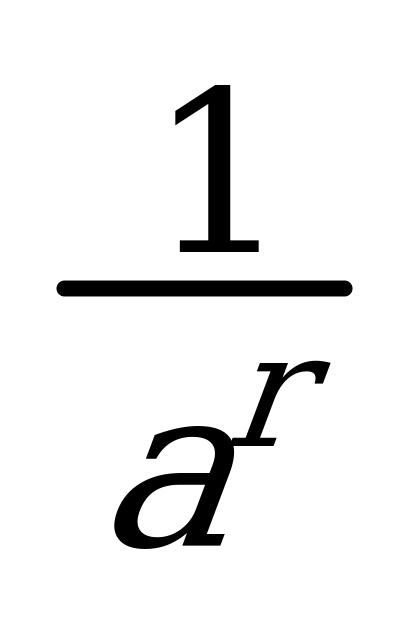 9.
9. 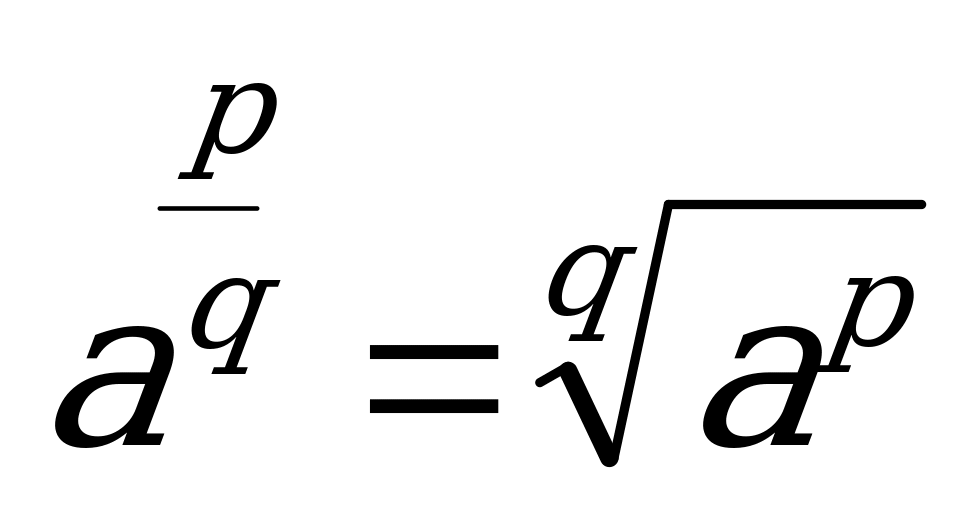 3. (a - b)2 = a2 - 2ab + b2
3. (a - b)2 = a2 - 2ab + b2
(arcctg x)¢ = -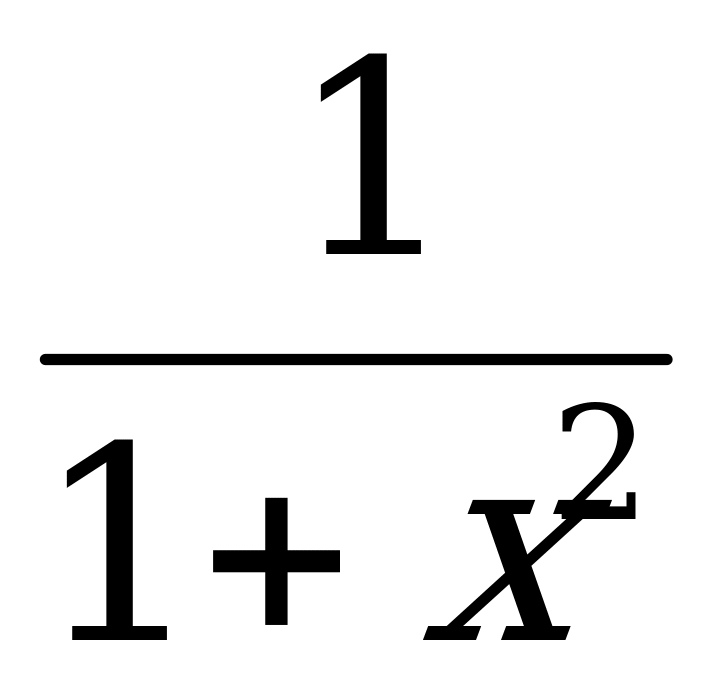 10. если 0 то 11. если r s, то 4. a3 – b3 = (a – b)( a2 + ab + b2)
10. если 0 то 11. если r s, то 4. a3 – b3 = (a – b)( a2 + ab + b2)
Уравнение касательной: ar br при r 0 ar as при a 1 5. a3 + b3 = (a + b)( a2 - ab + b2)
y = f(a) + f /(a)(x – a) ar r при r r s при 0 (a + b)3 = a3 + 3a2 b + 3ab2 + b3
7. (a - b)3 = a3 - 3a2 b + 3ab2 - b3
 Свойства корней Арифметическая прогрессии Геометрическая Симметрические системы
Свойства корней Арифметическая прогрессии Геометрическая Симметрические системы
1. 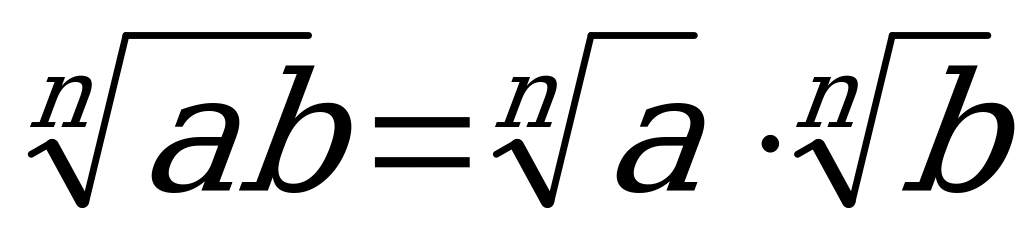 2.
2. 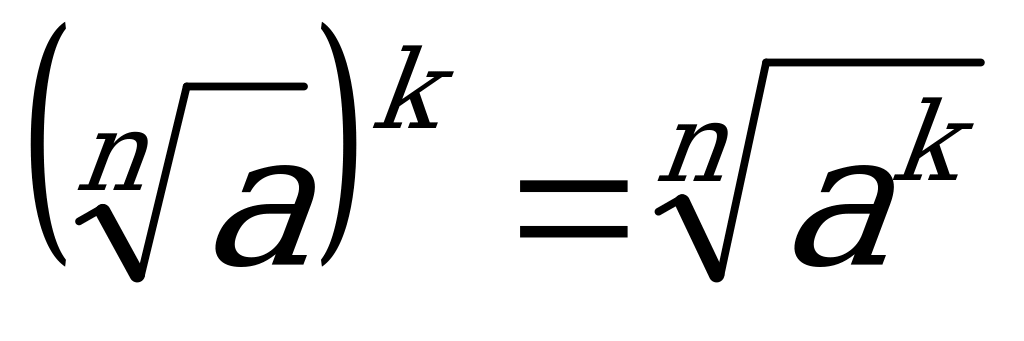 1. an = a1 + d(n – 1). 1. bn = b1qn - 1 1. х + у = u, xy = v 2. x2 + у2 = u2 – 2v
1. an = a1 + d(n – 1). 1. bn = b1qn - 1 1. х + у = u, xy = v 2. x2 + у2 = u2 – 2v
3. 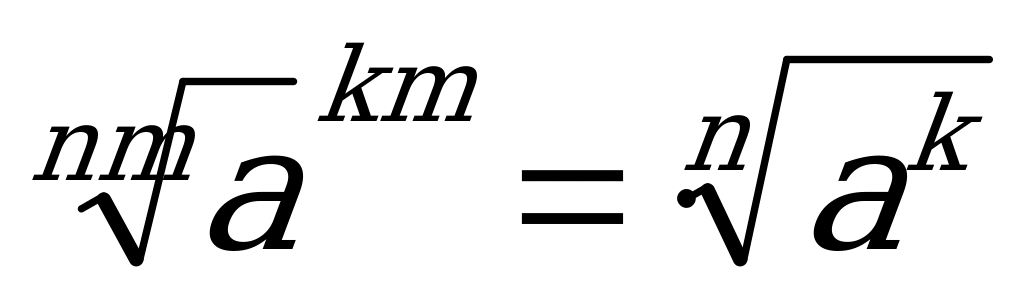 4.
4. 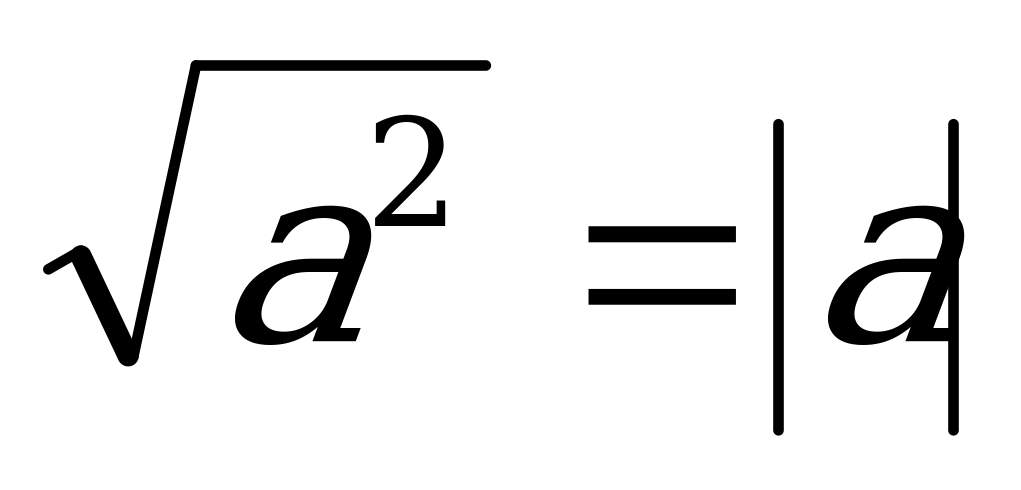 2. Sn =
2. Sn = 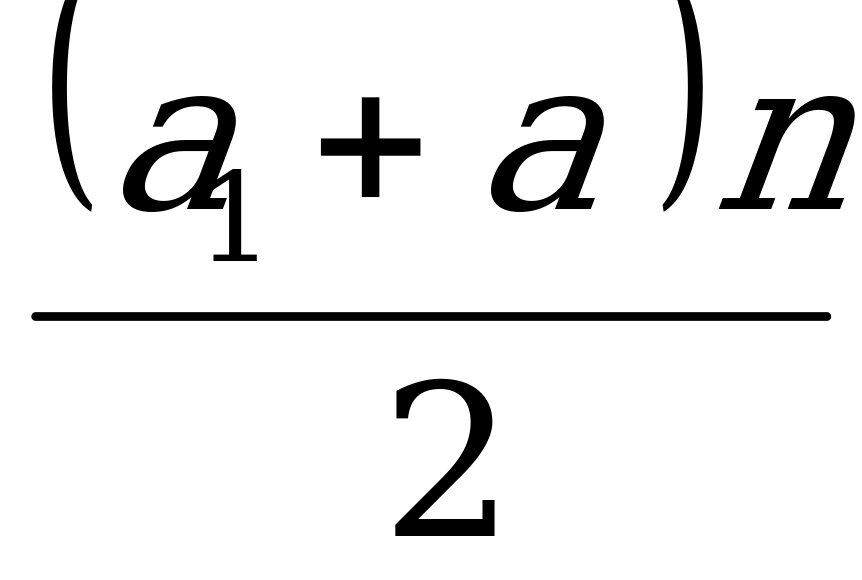 =
= 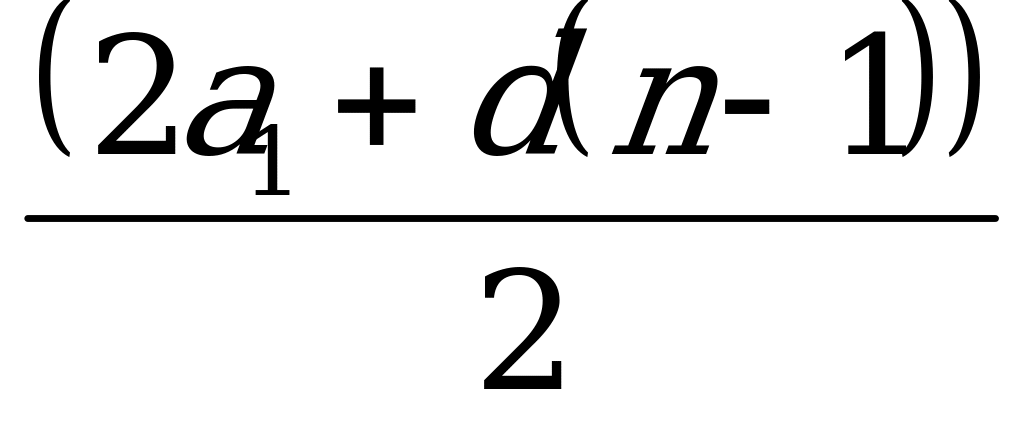 2. Sn =
2. Sn =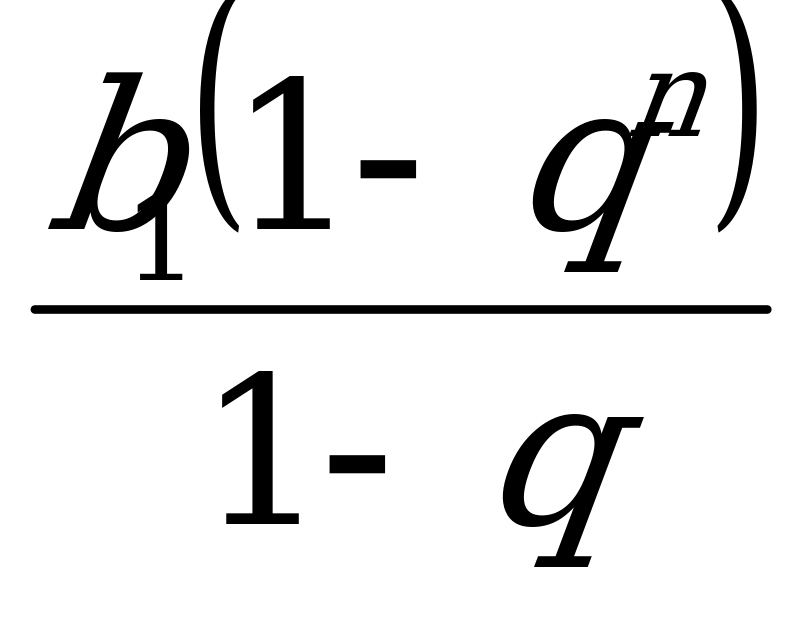 =
= 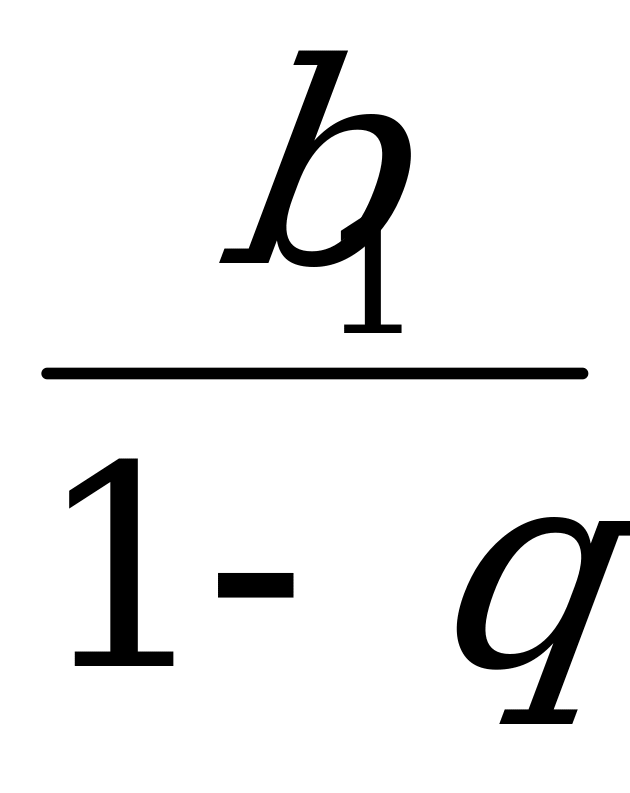 3. x3 + y3 = u3 – 3uv 4. x4 + y4 = u4 – 4u2v + 2v2
3. x3 + y3 = u3 – 3uv 4. x4 + y4 = u4 – 4u2v + 2v2
5. 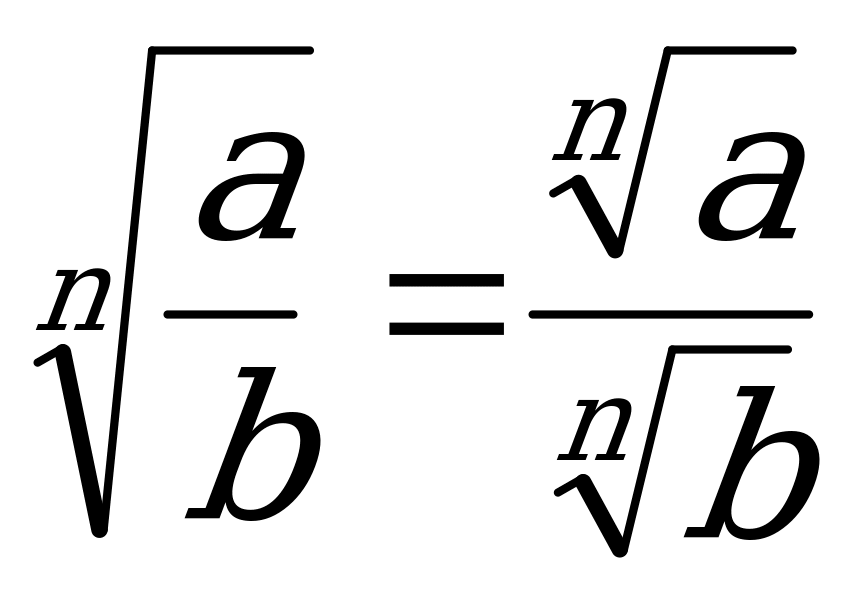 6.
6. 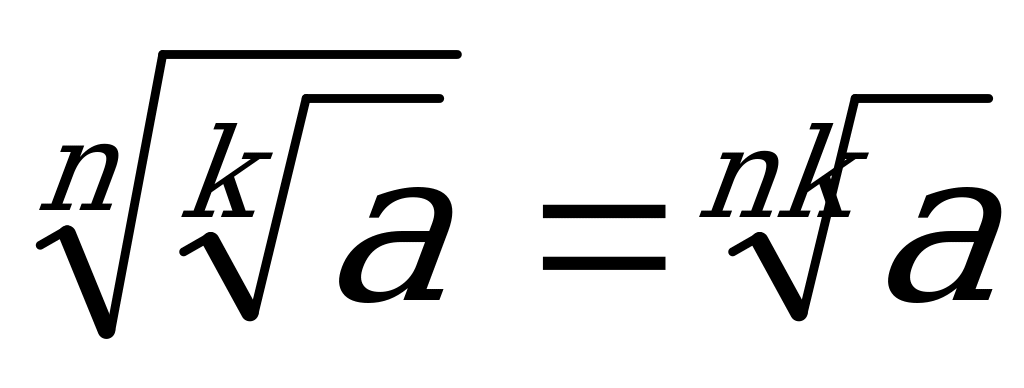 3. an =
3. an =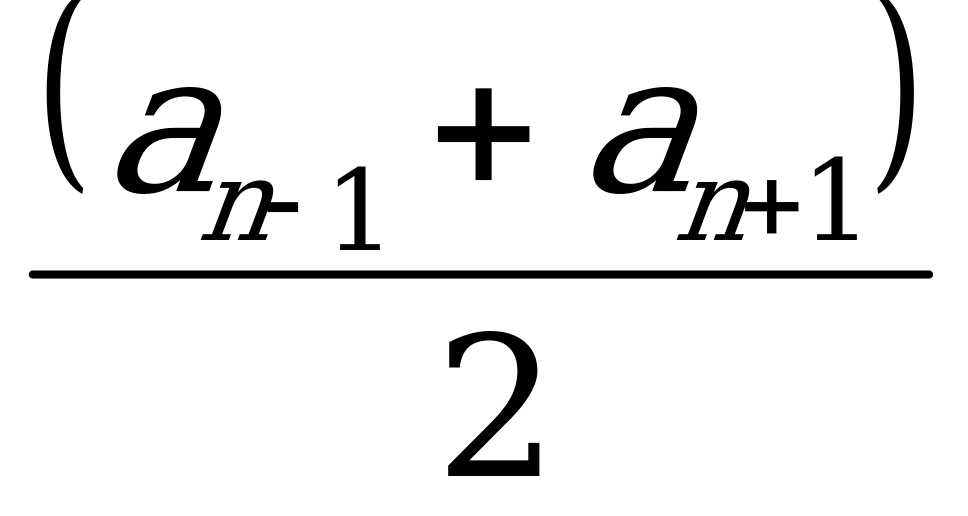 3. bn =
3. bn = 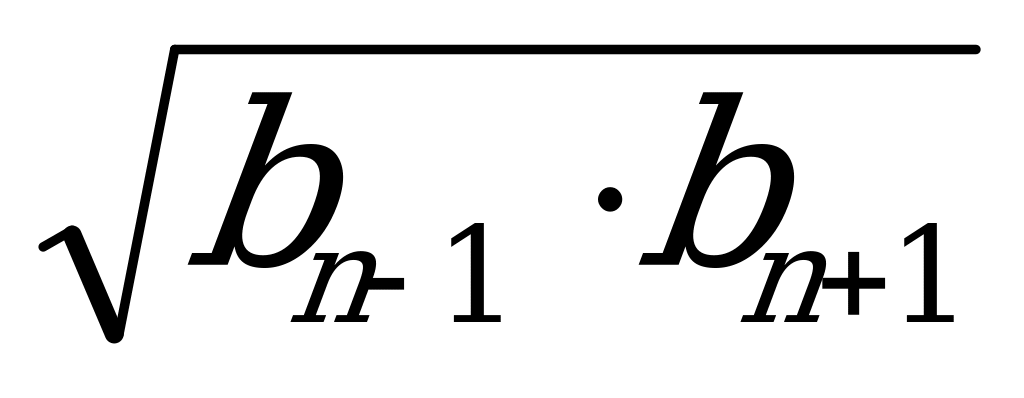 5. x5 + y5 = u5 – 5u3v + 5uv3
5. x5 + y5 = u5 – 5u3v + 5uv3





 ригонометрия
ригонометрия

 . sin2x + cos2x = 1 6. sin 2x = 2sin x*cos x 11. cos2x =
. sin2x + cos2x = 1 6. sin 2x = 2sin x*cos x 11. cos2x = 

 . tg x + ctg x =
. tg x + ctg x = 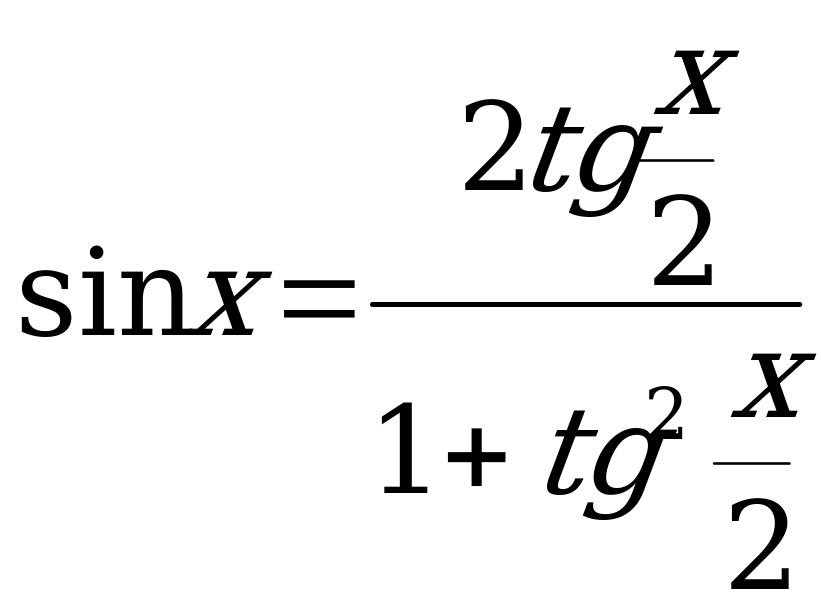 32.
32. 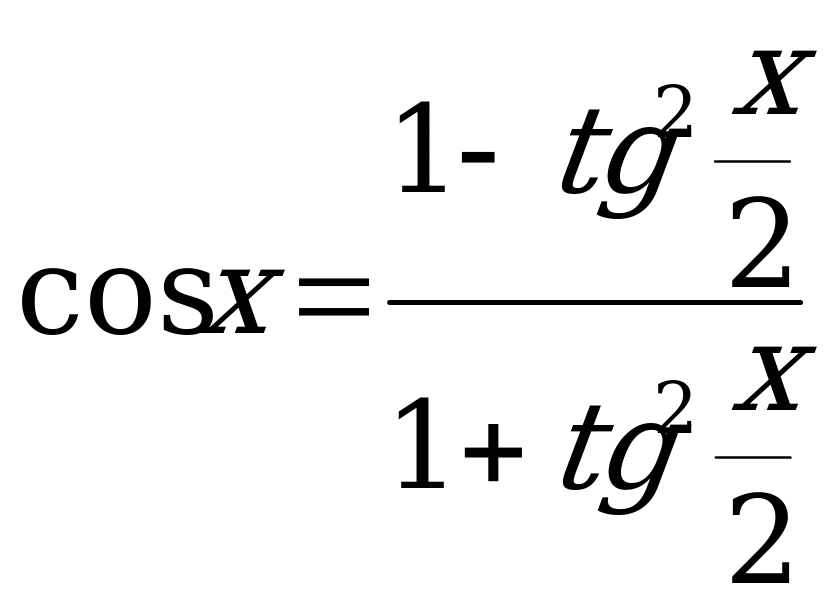

 16. cos(x + y) = cos x*cosy - sinx*siny 20. cosx*cosy =
16. cos(x + y) = cos x*cosy - sinx*siny 20. cosx*cosy =  вадратное уравнение: ax2 + bx + c = 0 ax2 + bx + c = a(x – x1)(x – x2) 1. tg x = 0, x = πn. 2. tg x = ± 1, x = ±
вадратное уравнение: ax2 + bx + c = 0 ax2 + bx + c = a(x – x1)(x – x2) 1. tg x = 0, x = πn. 2. tg x = ± 1, x = ± 
 Правила дифференцирования Правила интегрирования Логарифмы
Правила дифференцирования Правила интегрирования Логарифмы 0.(ln x)¢ =
0.(ln x)¢ =  Свойства корней Арифметическая прогрессии Геометрическая Симметрические системы
Свойства корней Арифметическая прогрессии Геометрическая Симметрические системы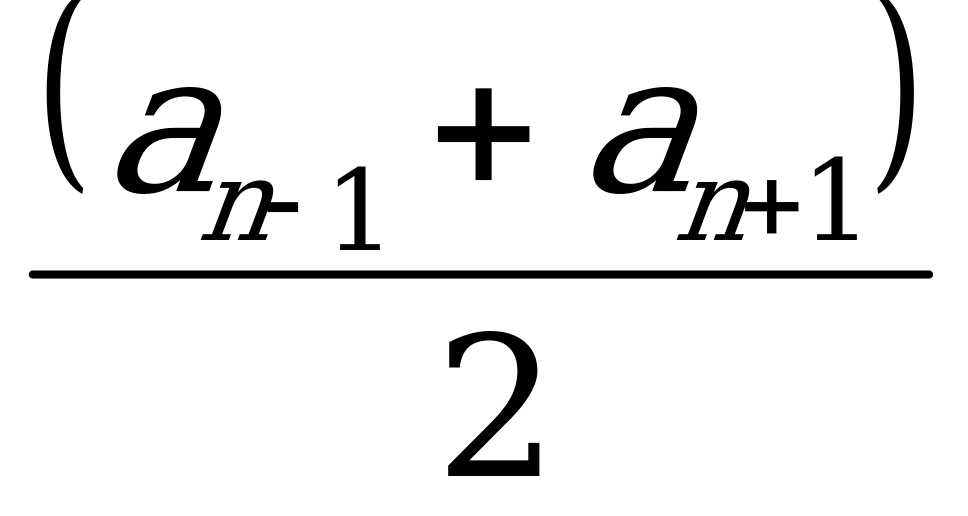 3. bn =
3. bn = 









