Формулы приведения

ФОРМУЛЫ ПРИВЕДЕНИЯ

История тригонометрии

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук

Леонард Эйлер

Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения.

Основные тригонометрические тождества (ОТТ)

Что такое формулы приведения?

Формулы приведения — это соотношения, которые позволяют перейти от тригонометрических функций  sin , cos , tg и ctg с углами π/2±α, π±α, 3π/2±α, 2π±α к этим же функциям угла α, который находится в первой четверти единичной окружности.

Таким образом, формулы приведения «приводят» нас к работе с углами в пределе от 0 до 90 градусов, что очень удобно.

Чтобы воспользоваться таблицей (см. предыдущий слайд), нужно выбрать строку с нужной нам функцией, и столбец с нужным аргументом. Например, чтобы узнать с помощью таблицы, чему будет равно sin(π+α), достаточно найти ответ на пересечении строки sinα и столбца π+α. Получим sin(π+α)=−sin α

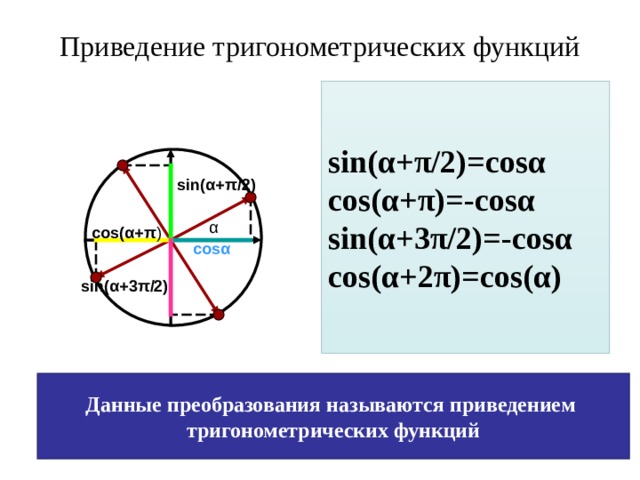
Приведение тригонометрических функций

sin( α + π /2)=cos α

cos( α + π )=-cos α

sin( α + 3 π /2 )=-cos α

cos( α + 2 π )=cos( α )

sin( α + π /2 )

α

cos( α + π )

cos α

sin( α +3 π /2)

Данные преобразования называются приведением

тригонометрических функций

МНЕМОНИЧЕСКОЕ ПРАВИЛО

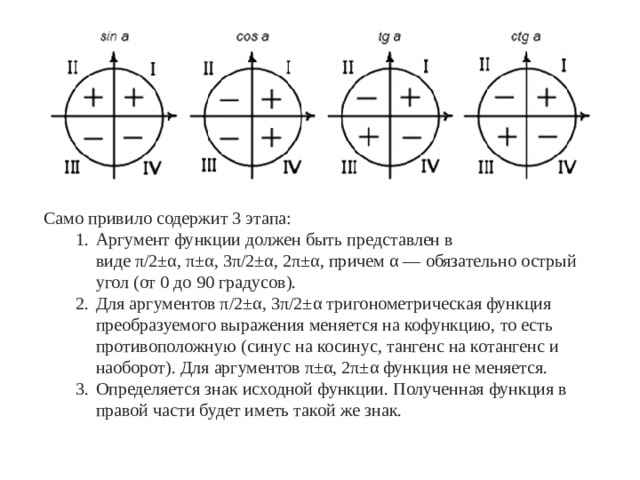
Само привило содержит 3 этапа:

• Аргумент функции должен быть представлен в виде π/2±α, π±α, 3π/2±α, 2π±α, причем α — обязательно острый угол (от 0 до 90 градусов). Для аргументов π/2±α, 3π/2±α тригонометрическая функция преобразуемого выражения меняется на кофункцию, то есть противоположную (синус на косинус, тангенс на котангенс и наоборот). Для аргументов π±α, 2π±α функция не меняется. Определяется знак исходной функции. Полученная функция в правой части будет иметь такой же знак.
• Аргумент функции должен быть представлен в виде π/2±α, π±α, 3π/2±α, 2π±α, причем α — обязательно острый угол (от 0 до 90 градусов).
• Для аргументов π/2±α, 3π/2±α тригонометрическая функция преобразуемого выражения меняется на кофункцию, то есть противоположную (синус на косинус, тангенс на котангенс и наоборот). Для аргументов π±α, 2π±α функция не меняется.
• Определяется знак исходной функции. Полученная функция в правой части будет иметь такой же знак.

Пример 1.  cos(π+α)

Пример 2. sin(3π/2—α)

• Функция на противоположную не меняется.
• Угол π+α находится в III четверти, косинус в этой четверти имеет знак «-» , поэтому преобразованная функция будет также со знаком «-» .

• Согласно мнемоническому правилу функция изменится на противоположную.
• Угол 3π/2—α находится в III четверти, синус здесь имеет знак «-» , поэтому результат также будет со знаком «-» .

Ответ: cos(π+α)=—cosα

Ответ: sin(3π2—α)=—cosα

ЗАДАНИЕ 1

• Вычислите при помощи формул приведения а)  sin600, б)  tg480 , в) cos330, г)  sin240
• Решение: а)  sin600=sin(2⋅270+60)=−cos60=−12sin600=

sin(2⋅270+60)=-cos60=-12;

ДОМАШНЕЕ ЗАДАНИЕ

• tg( π /2+ α ) =
• ctg(3 π /2- α ) =
• cos( 3 π /2+ α ) =
• sin( π - α ) =

ДОМАШНЕЕ ЗАДАНИЕ