Функции и их графики

Повторение

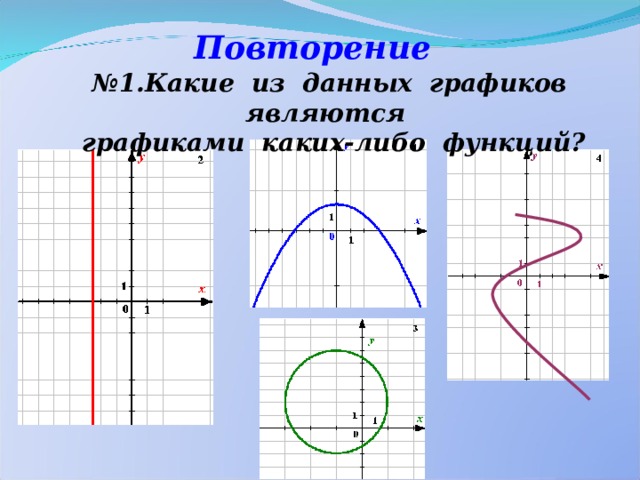
№ 1.Какие из данных графиков являются

графиками каких-либо функций?

№ 2 . Повторение

Линейные функции.

y = ах + b

№ 2. Повторение.

Функции прямой пропорциональности.

у = kx

№ 2. Повторение.

Функции обратной пропорциональности.

у = k / x

№ 2. Повторение.

Квадратичные функции.

у = ах 2 + bx +c

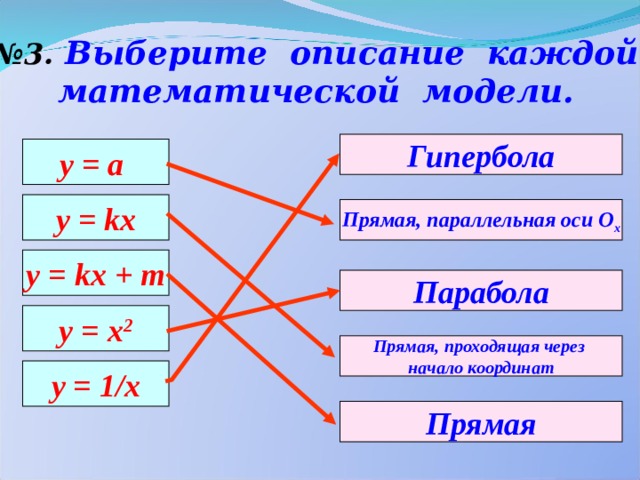
№ 3. Выберите описание каждой

математической модели.

Гипербола

у = а

y = kx

Прямая, параллельная оси О х

y = kx + m

Парабола

y = x 2

Прямая, проходящая через

начало координат

y = 1/x

Прямая

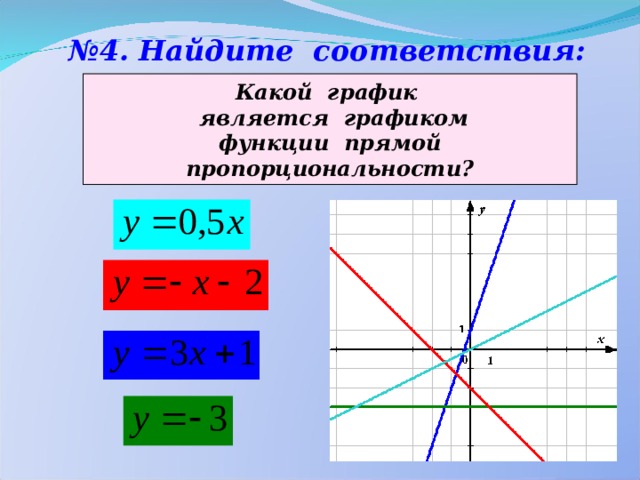
№ 4. Найдите соответствия:

Какой график

является графиком

функции прямой

пропорциональности?

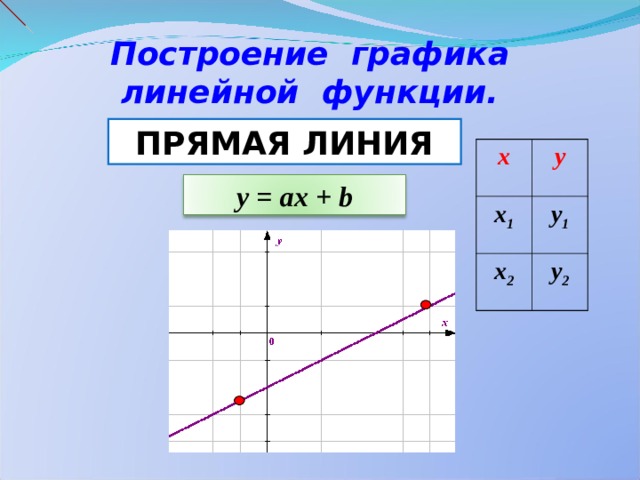
Построение графика линейной функции.

ПРЯМАЯ ЛИНИЯ

х

у

х 1

у 1

х 2

у 2

y = ах + b

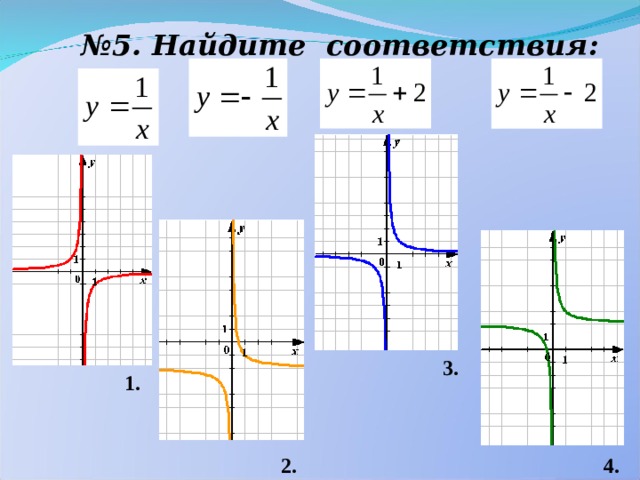
№ 5. Найдите соответствия:

3.

1.

2.

4.

0 – I u III ч. k ч. 2. Составить таблицу значений функции. " width="640"

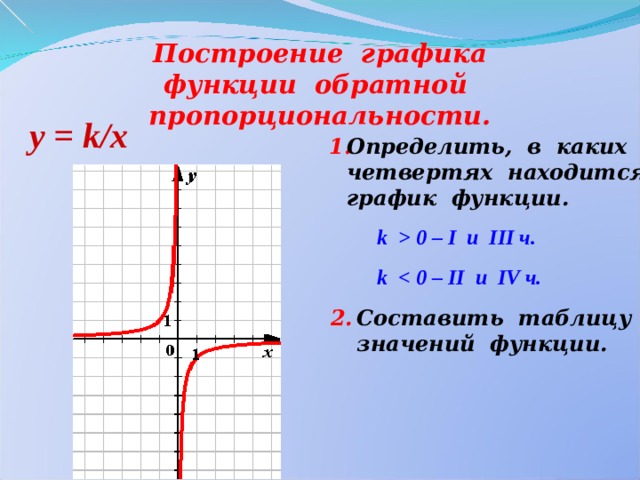
Построение графика функции обратной пропорциональности.

у = k / x

1.

Определить, в каких

четвертях находится

график функции.

k 0 – I u III ч.

k ч.

2.

Составить таблицу

значений функции.

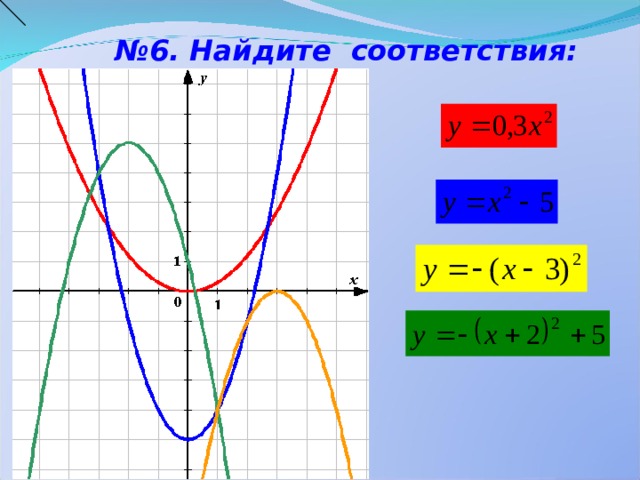
№ 6. Найдите соответствия:

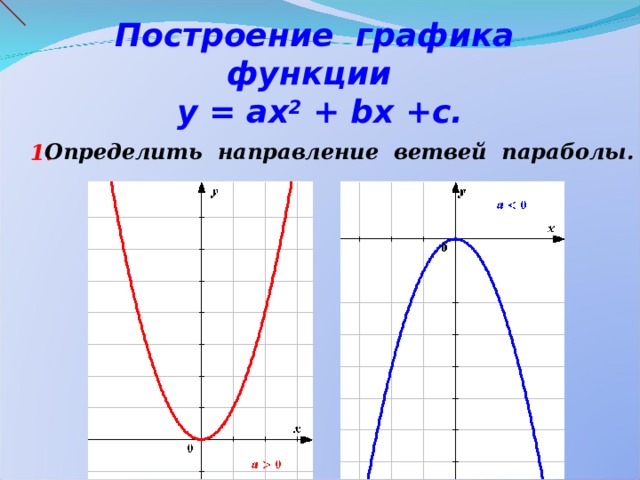
Построение графика функции у = ах 2 + b х +с.

Определить направление ветвей параболы.

1.

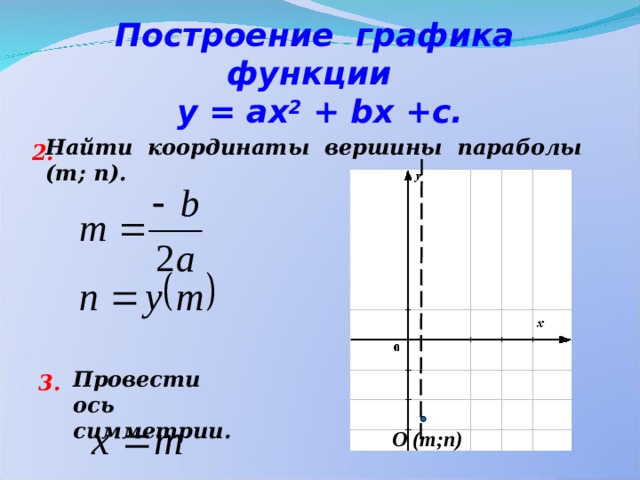
Построение графика функции у = ах 2 + b х +с.

Найти координаты вершины параболы

(т; п).

2.

Провести ось

симметрии.

3.

О (т;п)

Построение графика функции у = ах 2 + b х +с.

Определить точки пересечения графика

функции с осью О х , т.е. найти нули

функции.

4.

(х 1 ;0)

(х 2 ;0)

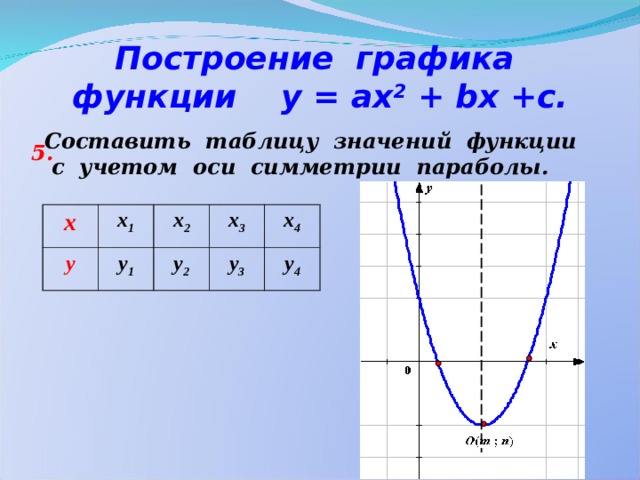
Построение графика функции у = ах 2 + b х +с.

Составить таблицу значений функции

с учетом оси симметрии параболы.

5.

х

у

х 1

х 2

у 1

у 2

х 3

у 3

х 4

у 4

Алгоритм построения графика функции у = ах 2 + b х +с.

1.

Определить направление ветвей параболы.

Найти координаты вершины параболы

(т; п).

2.

3.

Провести ось симметрии.

Определить точки пересечения графика

функции с осью О х , т.е. найти нули

функции.

4.

5.

Составить таблицу значений функции

с учетом оси симметрии параболы.