Дата проведения:
Тема урока: Функции и их графики.
Цели урока: 1)Образовательная: Обобщить знания об изученных функциях и их свойствах. Рассмотреть применение функций в различных областях знаний. Проверить усвоение учащимися данной темы.
2)Развивающая: Развивать мыслительную деятельность, творческие способности и логическое мышление учащихся.
3)Воспитательная: воспитывать познавательную активность, культуру общения, прививать интерес к предмету
Тип урока: обобщение знаний
Литература: Погорелов
Оборудование: карточки, доска.
Ход урока
- Организационный момент. Сообщение темы и цели урока.
- Повторение
Новая тема
Функция y=f(x)y=f(x) — это такая зависимость переменной y от переменной x, когда каждому допустимому значению переменной x соответствует единственное значение переменной y.
Областью определения функции D(f)D(f) называют множество всех допустимых значений переменной x.
Область значений функции E(f)E(f) — множество всех допустимых значений переменной y.
График функции y=f(x)y=f(x) — множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости, то есть точек, вида M (x; f(x))(x;f(x)). График функции представляет собой некоторую линию на плоскости.
Линейной функцией называют функцию, которую можно задать формулой:

График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону - слева направо):

График квадратичной функции (Парабола)
График параболы задается квадратичной функцией: 

При этом:
- если коэффициент a > 0, в функции y = ax2 + bx + c, то ветви параболы направлены вверх;
- если же a < 0, то ветви параболы направлены вниз.
Степенной функцией называют функцию, заданную формулой:

- Закрепление Пример 1 Построить график функции у=-х2+2х.
Рассчитываем соответствующее значение «игрек»: у=-12+2·1=-1+2=1. Таким образом, вершина находится в точке (1; 1).
1 вариант
у=х2, 1) у=x2+2x+3;
у=х2+4,
у=(х-3)2.
2 вариант
у=х2,
у=(х+1)2, 1) у=x2-4x;
у=х2-2.
3 вариант
у=х3,
у=х3+1, 1) у=-x2+2x-1;
у=(х-2)3.
- Итог урока
-Что называется функцией?
-Что является графиком линейной, квадратичной функций?
Оценивание, Д/задание у=х2-5.
Просмотр содержимого документа
«Функции и их графики.»
Дата проведения:
Тема урока: Функции и их графики.
Цели урока: 1)Образовательная: Обобщить знания об изученных функциях и их свойствах. Рассмотреть применение функций в различных областях знаний. Проверить усвоение учащимися данной темы.
2)Развивающая: Развивать мыслительную деятельность, творческие способности и логическое мышление учащихся.
3)Воспитательная: воспитывать познавательную активность, культуру общения, прививать интерес к предмету
Тип урока: обобщение знаний
Литература: Погорелов
Оборудование: карточки, доска.
Ход урока
Организационный момент. Сообщение темы и цели урока.
Повторение
Новая тема
Функция y=f(x)y=f(x) — это такая зависимость переменной y от переменной x, когда каждому допустимому значению переменной x соответствует единственное значение переменной y.
Областью определения функции D(f)D(f) называют множество всех допустимых значений переменной x.
Область значений функции E(f)E(f) — множество всех допустимых значений переменной y.
График функции y=f(x)y=f(x) — множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости, то есть точек, вида M (x; f(x))(x;f(x)). График функции представляет собой некоторую линию на плоскости.
Линейной функцией называют функцию, которую можно задать формулой:
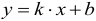
График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k 0, в этом случае функция возрастающая; для случая k
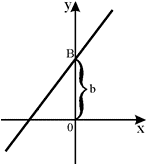
График квадратичной функции (Парабола)
График параболы задается квадратичной функцией: 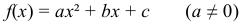
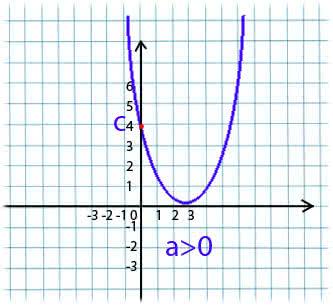
При этом:
если коэффициент a 0, в функции y = ax2 + bx + c, то ветви параболы направлены вверх;
если же a
Степенной функцией называют функцию, заданную формулой:
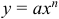
Закрепление Пример 1 Построить график функции у=-х2+2х.
Рассчитываем соответствующее значение «игрек»: у=-12+2·1=-1+2=1. Таким образом, вершина находится в точке (1; 1).
1 вариант
у=х2, 1) у=x2+2x+3;
у=х2+4,
у=(х-3)2.
2 вариант
у=х2,
у=(х+1)2, 1) у=x2-4x;
у=х2-2.
3 вариант
у=х3,
у=х3+1, 1) у=-x2+2x-1;
у=(х-2)3.
Итог урока
-Что называется функцией?
-Что является графиком линейной, квадратичной функций?
Оценивание, Д/задание у=х2-5.























