Россия, Михайловск
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 17.12.2022 23:17
Ковалева Евгения Дмитриевна
учитель математики
66 лет
1 191
51 389 
Местоположение
Специализация
Функции и их свойства
Категория:
Алгебра
17.12.2022 22:55
Просмотр содержимого документа
«Функции и их свойства»
.
Повторение. «Функции и их свойста».
№ 1.Какие из данных графиков являются
графиками каких-либо функций?
Повторение.
№ 2 . Повторение.
Линейные функции.
y = ах + b
Верно!
№ 2. Повторение.
Функции прямой пропорциональности.
у = kx
Правильно!
№ 2. Повторение.
Функции обратной пропорциональности.
у = k / x
И все!
№ 2. Повторение.
Квадратичные функции.
у = ах 2 + bx +c
Молодцы!
№ 3. Выберите описание каждой
математической модели.
Гипербола
у = а
y = kx
Прямая, параллельная оси О х
y = kx + m
Парабола
y = x 2
Прямая, проходящая через
начало координат
y = 1/x
Прямая
Повторение.
№ 4. Найдите соответствия:
Какой график
является графиком
функции прямой
пропорциональности?
Построение графика линейной функции.
y = ах + b
х
у
х 1
у 1
х 2
у 2
Экзаменационный
сборник: № 174 (2)
№ 5. Найдите соответствия:
1.
3.
2.
4.
0 – I u III ч. k ч. 2. Составить таблицу значений функции. Экзаменационный сборник: №175(2) " width="640"
Построение графика функции обратной пропорциональности.
у = k / x
1.
Определить, в каких
четвертях находится
график функции.
k 0 – I u III ч.
k ч.
2.
Составить таблицу
значений функции.
Экзаменационный
сборник: №175(2)
№ 6. Найдите соответствия:
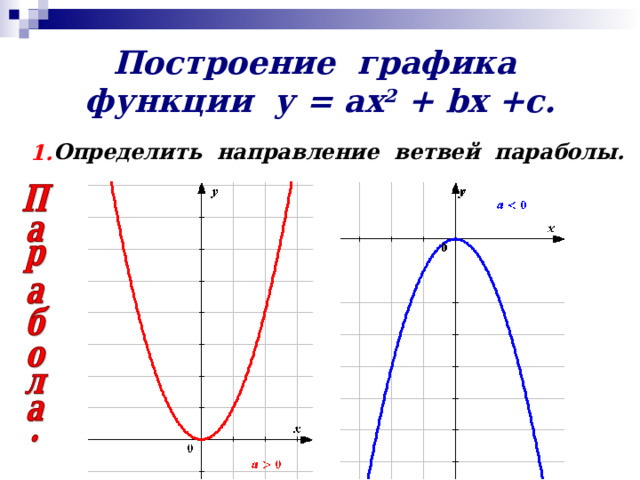
Построение графика функции у = ах 2 + b х +с.
Определить направление ветвей параболы.
1.
Построение графика функции у = ах 2 + b х +с.
Найти координаты вершины параболы
(т; п).
2.
Провести ось
симметрии.
3.
О (т;п)
Построение графика функции у = ах 2 + b х +с.
Определить точки пересечения графика
функции с осью О х , т.е. найти нули
функции.
4.
(х 1 ;0)
(х 2 ;0)
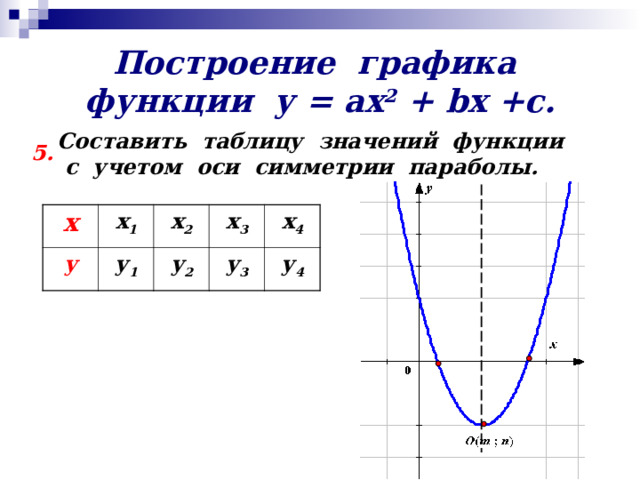
Построение графика функции у = ах 2 + b х +с.
Составить таблицу значений функции
с учетом оси симметрии параболы.
5.
х
у
х 1
х 2
у 1
у 2
х 3
х 4
у 3
у 4
Алгоритм построения графика функции у = ах 2 + b х +с.
1.
Определить направление ветвей параболы.
Найти координаты вершины параболы
(т; п).
2.
3.
Провести ось симметрии.
Определить точки пересечения графика
функции с осью О х , т.е. найти нули
функции.
4.
5.
Составить таблицу значений функции
с учетом оси симметрии параболы.
Экзаменационный сборник: № 11.
Домашнее задание:
сборник тестов:
№ 11
№ 22
- Каков вид графика функции
обратной пропорциональности?
1.
г
и
п
е
р
б
о
л
а
- Каков вид графика
квадратичной функции?
2.
п
1.
а
р
г
а
и
б
п
е
о
л
р
а
б
о
л
а
3.
3. Как называется
координата
точки по оси Ох?
а
б
2.
с
п
ц
а
1.
и
р
г
а
с
и
с
б
п
е
о
а
л
р
а
б
о
л
а
4.
о
3.
4. Как называется
координата
точки по оси Оу?
р
а
б
д
2.
и
п
с
ц
а
1.
н
и
а
р
г
с
а
т
и
с
б
п
а
е
о
а
л
р
а
б
о
л
а
4.
о
3.
5. Один из способов задания
функции.
р
а
б
д
2.
и
с
п
ц
а
1.
н
5.
р
и
ф
а
г
с
а
о
т
и
б
с
п
а
р
е
о
м
а
у
л
р
а
л
б
а
о
л
а
4.
о
3.
6. Переменная величина,
значение которой зависит
от изменения другой
величины.
а
р
6.
ф
б
д
2.
у
и
с
п
н
ц
н
а
1.
5.
к
р
а
и
г
ф
ц
а
с
о
т
и
с
б
и
п
а
р
е
о
я
м
а
л
у
р
л
а
б
а
о
л
а
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
