Функции y=x2 и y=x3 и их графики.

Функции у = х 2 и у = х 3 и их графики

Построить график функции

у= 2х-3

Функции

у = х 2 и у = х 3

и их графики

0. График расположен в I и II координатных четвертях. 5. Противоположным значениям х соответствует одно и то же значение у : (-х) 2 = х 2 . Говорят, что ветви параболы симметричны относительно оси ОУ. y = x 2 " width="640"

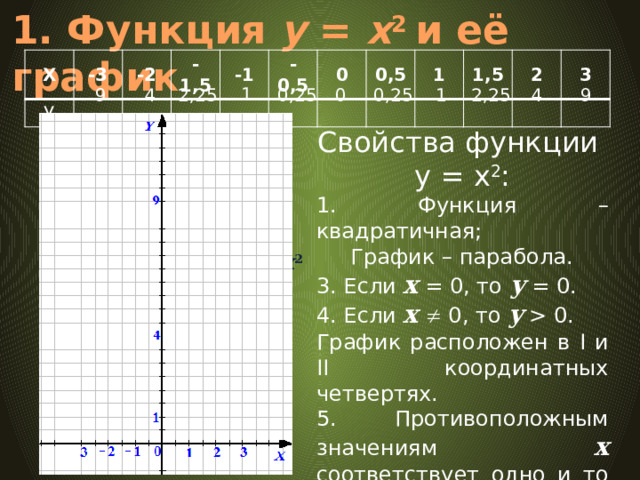
1. Функция у = х 2 и её график

Х

У

-3

-2

-1,5

-1

-0,5

0

0,5

1

1,5

2

3

1

0,25

2,25

9

0,25

0

1

4

2,25

4

9

Свойства функции у = x 2 :

1. Функция – квадратичная;

График – парабола.

3. Если х = 0, то у = 0.

4. Если х  0, то y 0.

График расположен в I и II координатных четвертях.

5. Противоположным значениям х соответствует одно и то же значение у : (-х) 2 = х 2 .

Говорят, что ветви параболы симметричны относительно оси ОУ.

y = x 2

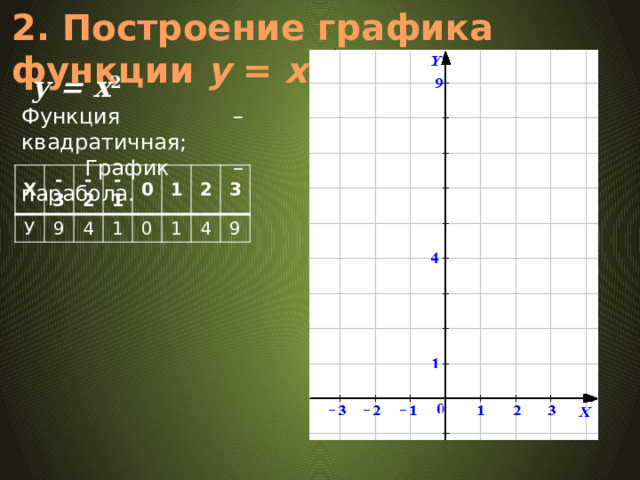
2. Построение графика функции у = х 2

у = x 2

Функция – квадратичная;

График – парабола.

Х

У

-3

9

-2

-1

4

1

0

1

0

1

2

4

3

9

y = x 2

0, то y 0, если х y График расположен в I и III координатных четвертях. 4. Противоположным значениям х соответствуют противоположные значения у : (-х) 3 = - х 3 . Говорят, что ветви кубической параболы симметричны относительно точки (0; 0). y = x 3 " width="640"

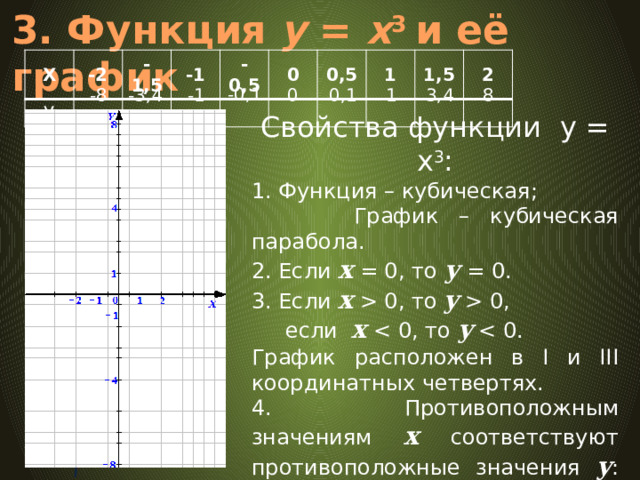
3. Функция у = х 3 и её график

Х

У

-2

-1,5

-1

-0,5

0

0,5

1

1,5

2

-0,1

0

0,1

3,4

8

1

-1

-3,4

-8

Свойства функции у = x 3 :

1. Функция – кубическая;

График – кубическая парабола.

2. Если х = 0, то у = 0.

3. Если х 0, то y 0,

если х y

График расположен в I и III координатных четвертях.

4. Противоположным значениям х соответствуют противоположные значения у : (-х) 3 = - х 3 .

Говорят, что ветви кубической параболы симметричны относительно точки (0; 0).

y = x 3

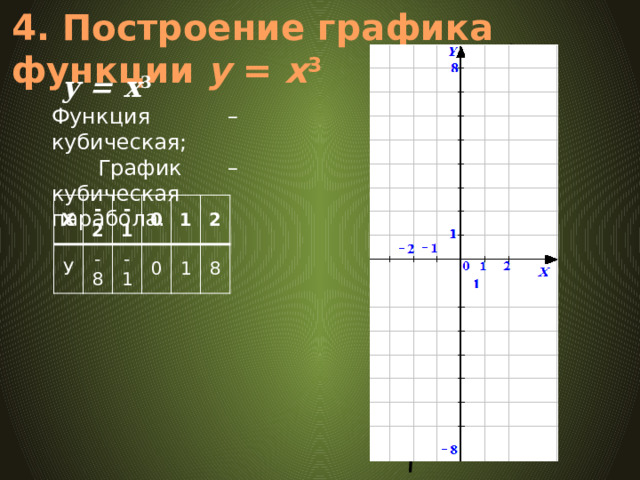
4. Построение графика функции у = х 3

у = x 3

Функция – кубическая;

График – кубическая парабола.

y = x 3

Х

-2

У

-8

-1

-1

0

0

1

2

1

8