Функция квадратного корня задаётся формулой 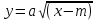 + n , где a0
+ n , где a0
I. Частным случаем функции квадратного корня является функция 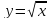
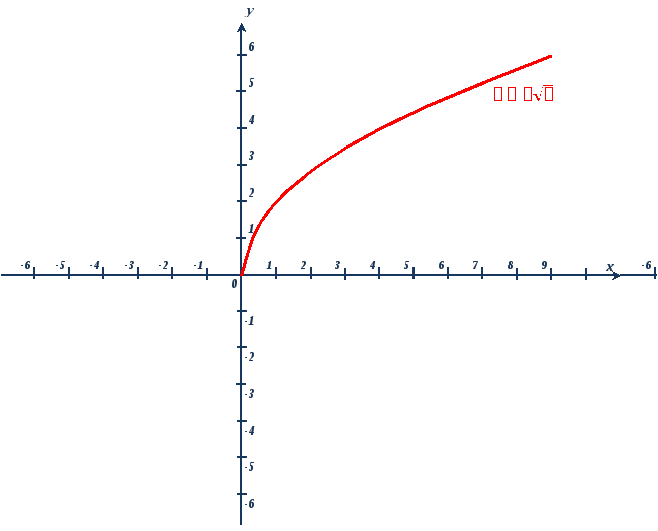
Графиком функции 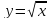 является ветвь параболы с вершиной в точке (0;0), проходящая через точки (1;1), (4;2), (9;3) (запомнить эти точки), располагается в I четверти.
является ветвь параболы с вершиной в точке (0;0), проходящая через точки (1;1), (4;2), (9;3) (запомнить эти точки), располагается в I четверти.
1) Область определения функции - множество всех положительных чисел и нуля: D(y)=[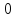 ; +
; +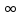 ).
).
2) Область значений функции – множество всех положительных чисел и нуля: E(y)=[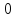 ; +
; +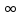 ).
).
3) Так как х не может быть отрицательным, то чётность этой функции не рассматривается. Она не является ни чётной, ни нечётной.
4) Функция возрастает при х 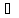 (0; +
(0; + 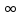 ).
).
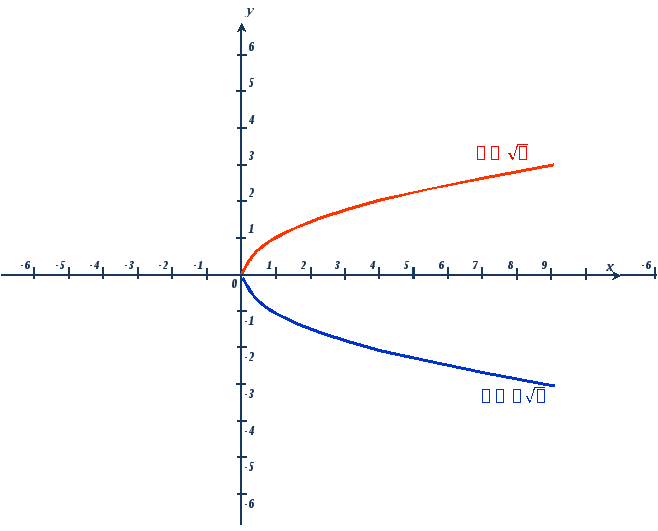
II. Частным случаем функции квадратного корня является функция 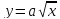 , где a 0
, где a 0
Графиком функции 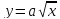 является ветвь параболы с вершиной в точке (0;0), располагается в I четверти.
является ветвь параболы с вершиной в точке (0;0), располагается в I четверти.
1) Область определения функции - множество всех положительных чисел и нуля: D(y)=[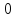 ; +
; +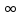 ).
).
2) Область значений функции – множество всех положительных чисел и нуля: E(y)=[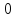 ; +
; +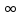 ).
).
3) Так как х не может быть отрицательным, то чётность этой функции не рассматривается. Она не является ни чётной, ни нечётной.
4) Функция возрастает при х  (0; +
(0; +  ).
).
III. Функция 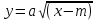 , где a 0
, где a 0
Графиком функции 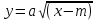 является ветвь параболы с вершиной в точке (m;0).
является ветвь параболы с вершиной в точке (m;0).
График функции 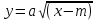 получается из графика функции
получается из графика функции 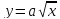 смещением вдоль оси Ox на m единиц.
смещением вдоль оси Ox на m единиц.
1) Область определения функции - множество всех положительных чисел и нуля: D(y)=[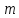 ; +
; +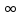 ).
).
2) Область значений функции – множество всех положительных чисел и нуля: E(y)=[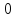 ; +
; +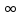 ).
).
3) Так как х не может быть отрицательным, то чётность этой функции не рассматривается. Она не является ни чётной, ни нечётной.
4) Функция возрастает при х 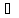 (m; +
(m; + 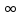 ).
).
IV. Функция  , где a 0
, где a 0
Графиком функции  является ветвь параболы с вершиной в точке (0; n).
является ветвь параболы с вершиной в точке (0; n).
График функции  получается из графика функции
получается из графика функции 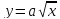 смещением вдоль оси Oy на n единиц.
смещением вдоль оси Oy на n единиц.
1) Область определения функции - множество всех положительных чисел и нуля: D(y)=[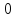 ; +
; +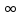 ).
).
2) Область значений функции – множество всех положительных чисел и нуля: E(y)=[ ; +
; +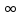 ).
).
3) Так как х не может быть отрицательным, то чётность этой функции не рассматривается. Она не является ни чётной, ни нечётной.
4) Функция возрастает при х 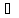 (0; +
(0; + 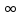 ).
).
V. Функция  , где a 0
, где a 0
Графиком функции  является ветвь параболы с вершиной в точке (m; n).
является ветвь параболы с вершиной в точке (m; n).
График функции  получается из графика функции
получается из графика функции 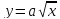 смещением вдоль оси Ox на m единиц и вдоль оси Oy на n единиц.
смещением вдоль оси Ox на m единиц и вдоль оси Oy на n единиц.
1) Область определения функции - множество всех положительных чисел и нуля: D(y)=[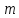 ; +
; +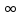 ).
).
2) Область значений функции – множество всех положительных чисел и нуля: E(y)=[ ; +
; +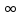 ).
).
3) Так как х не может быть отрицательным, то чётность этой функции не рассматривается. Она не является ни чётной, ни нечётной.
4) Функция возрастает при х 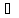 (m; +
(m; + 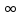 ).
).







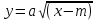 + n , где a0
+ n , где a0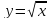
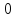 ; +
; +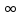 ).
). (0; +
(0; + 
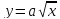 , где a 0
, где a 0
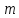 ; +
; +









