© 2016 10354 5


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Функція y = ax2 + bx + c, її властивості та графік.
Категория:
Математика
14.12.2016 15:33


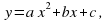 де
де 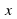 - незалежна змінна, a, b, c – числа ( а
- незалежна змінна, a, b, c – числа ( а 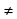 0), називається квадратичною функцією.
0), називається квадратичною функцією.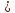 0, вітки параболи напрямлені вгору, якщо а
0, вітки параболи напрямлені вгору, якщо а 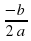 ; у0 = у(х0).
; у0 = у(х0).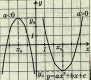
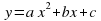
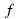 ): (
): ( ).
). ); при а
); при а  у0].
у0].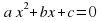 ;
;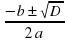 , при D
, при D 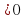 функція спадає, якщо хє(
функція спадає, якщо хє(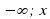 0],
0],









