Геометрическая вероятность. Случайный выбор точки из фигуры на плоскости, 9 класс

Геометрическая вероятность

• Иногда случайный опыт можно представить, как выбор точки из некоторой фигуры на плоскости или из промежутка на прямой.
• В таком опыте каждое отдельное элементарное событие имеет нулевую вероятность. Поэтому обычный способ подсчета вероятностей не подходит. На помощь приходит геометрическая вероятность.

• Интересно, что в геометрических случайных опытах удобно считать, что событие и фигура это одно и то же.
• Вероятности на плоскости измеряются отношением площадей фигур, на прямой отношением длин промежутков.

Урок 1

Выбор точки из фигуры на плоскости

Выбор точки из фигуры на плоскости

Неисправный пиксель на экране монитора компьютера.

Пикселей на экране может быль больше миллиона.

Удобно считать, что мы имеем дело с точкой, выбранной случайным образом из прямоугольника

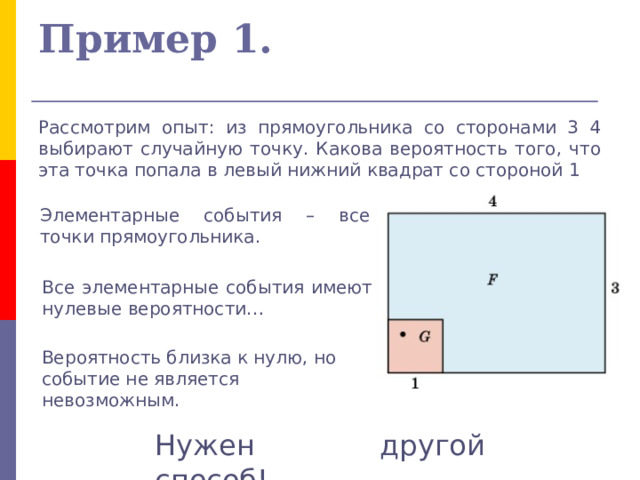
Пример 1.

Рассмотрим опыт: из прямоугольника со сторонами 3 4 выбирают случайную точку. Какова вероятность того, что эта точка попала в левый нижний квадрат со стороной 1

Элементарные события – все точки прямоугольника.

Все элементарные события имеют нулевые вероятности…

Вероятность близка к нулю, но событие не является невозможным.

Нужен другой способ!

Выбор точки из фигуры на плоскости Определение геометрической вероятности

Точку наудачу бросают в фигуру F на плоскости. Какова вероятность того, что точка попадёт в некоторую фигуру G , которая содержится в фигуре F ?

Вероятность события «выбранная точка принадлежит фигуре G прямо пропорциональна площади фигуры G и не зависит от расположения и формы фигуры G

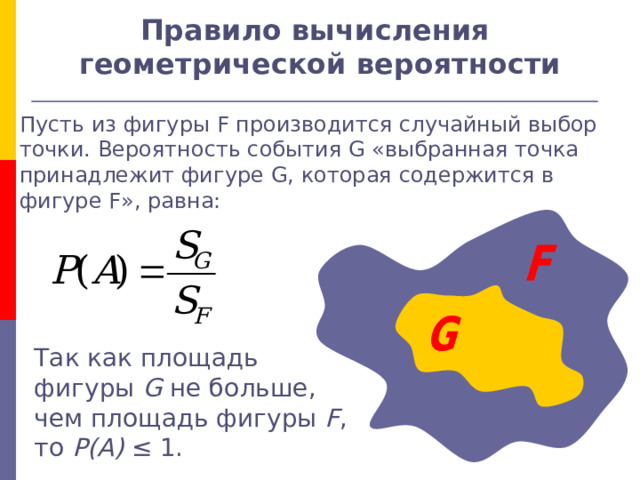
Правило вычисления геометрической вероятности

Пусть из фигуры F производится случайный выбор точки. Вероятность события G «выбранная точка принадлежит фигуре G , которая содержится в фигуре F », равна:

Так как площадь фигуры G не больше, чем площадь фигуры F , то P(A) ≤ 1.

Пример 1 (продолжение)

Рассмотрим опыт: из прямоугольника со сторонами 3 4 выбирают случайную точку. Какова вероятность того, что эта точка попала в левый нижний квадрат со стороной 1

Решая такие задачи, мы предполагаем, что «шансы любой точки одинаковы». В большинстве случайных опытов это не так, но при определенных условиях будем считать, что наше предположение недалеко от истины.

Выбор точки из фигуры на плоскости Пример 2

Стрелок стреляет издалека по круглой мишени диаметром 5 см. Известно, что стрелок попал в мишень, которая разбита на три зоны. Радиус центральной круговой зоны равен 1 см, средняя и внешняя зоны – кольцевые, они имеют одинаковую ширину 2 см. Найдем вероятность того, что стрелок попал во внешнюю зону мишени.

Решение:

Фигура F является мишенью – ее площадь

Площадь фигуры G -

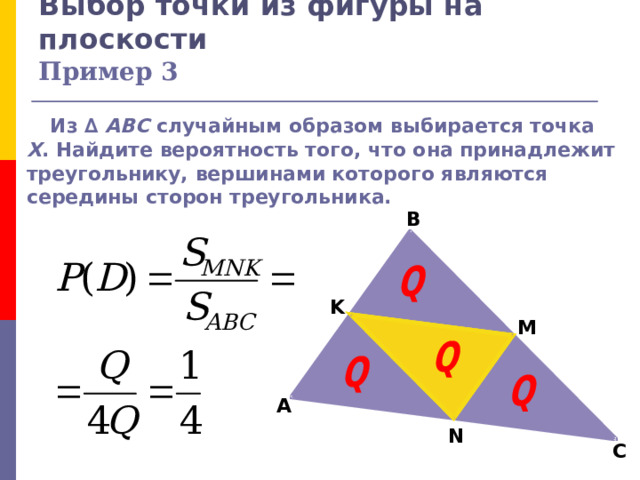
Выбор точки из фигуры на плоскости Пример 3

Из ∆ ABC случайным образом выбирается точка X . Найдите вероятность того, что она принадлежит треугольнику, вершинами которого являются середины сторон треугольника.

B

K

M

A

N

C

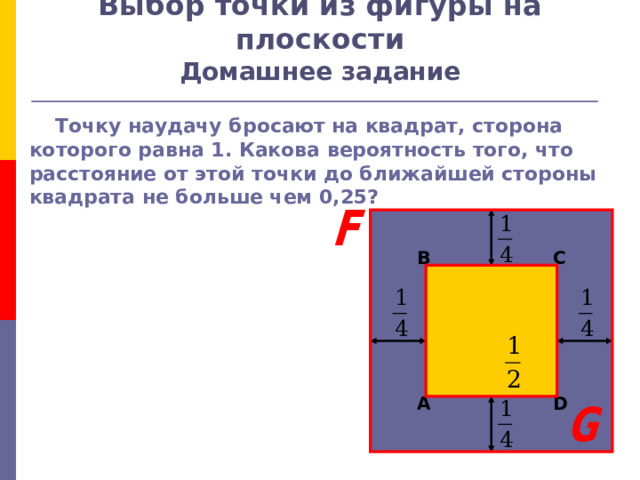
Выбор точки из фигуры на плоскости Домашнее задание

Точку наудачу бросают на квадрат, сторона которого равна 1. Какова вероятность того, что расстояние от этой точки до ближайшей стороны квадрата не больше чем 0,25?

B

C

A

D