Просмотр содержимого документа
«Геометрический материал (задачи на построение), (задачи на распознавание и деление фигур на части)»
| 
| Министерство образования, науки и молодёжной политики Краснодарского края |
| Государственное бюджетное профессиональное образовательное учреждение Краснодарского края «ЕЙСКИЙ ПОЛИПРОФИЛЬНЫЙ КОЛЛЕДЖ» |
Геометрический материал (задачи на построение), (задачи на распознавание фигур), (деление фигур на части), (составление фигур из заданных частей)
Выполнила:
студентка Ш-42 группы
Бузмакова Марина
Ейск, 2022г.
Задачи на построение
Задача 1. Построение отрезка, равного данному.
Дано: Построение:
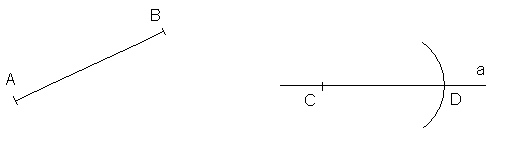
AB=CD.
Построить: [CD].
Проведем произвольную прямую а и отметим на ней точку С. Возьмем раствор циркуля, равный данному отрезку, и проведем окружность с центром в точке С. Одну из точек пересечения этой окружности с прямой а обозначим D. Полученный отрезок СD равен данному. Задача решена.
Приведенное решение выстроилось из основных операций: 1, 2 и 5. Если построение отрезка, равного данному, встретится в следующих задачах, то мы не будем его повторять, а будем считать, что мы его уже провели. Таким образом, каждая решенная задача будет расширять спектр наших возможностей.
Задача 2. Построение треугольника, равного данному.
Дано: Построение:
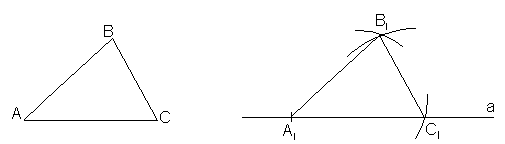
∆АВС=∆А1В1С1
Построить: ∆А1В1С1
На произвольной прямой а отложим отрезок А1С1 равный отрезку АС. Затем построим две окружности с центрами в концах отрезка А1С1, радиусы которых равны двум другим сторонам данного треугольника. Одну из точек пересечения окружностей обозначим В1. Соединив точки А1, В1 и С1, получим треугольник А1В1С1, равный треугольнику АВС.
3адача 5. Деление отрезка пополам.
Да но: Построение:
но: Построение:
[АВ];
Точка М лежит на [АВ];
АМ = МВ.
Построить:
точку М.
Построим две пересекающиеся окружности произвольного радиуса с центрами в концах данного отрезка АВ. Через точки С и D пересечения окружностей проведем прямую СD. Точка пересечения прямой СD с данным отрезком и есть искомая середина отрезка АВ.
Заметим, что прямая СD не только проходит через середину отрезка АВ, но и перпендикулярна к нему. Такую прямую называют серединным перпендикуляром к отрезку. Поэтому проведенное построение одновременно является и построением серединного перпендикуляра.
Задачи на распознавание фигур
Задача 1. Как называется эта фигура? Напишите её название: ___________.

З
адача 2. Сколько треугольников на рисунке: ___________.
Задача 3. Нарисуй черный прямоугольник. Две его стороны равны 5 см, а две другие равны 2 см.
Деление фигур на части
Задача 1.

Задача 2.

Задача 3.
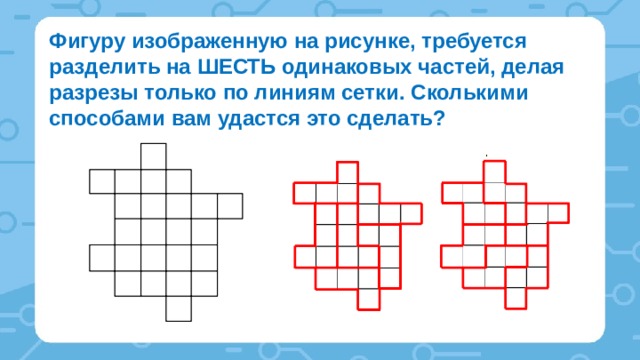
Составление фигур из заданных частей
Задача 1.
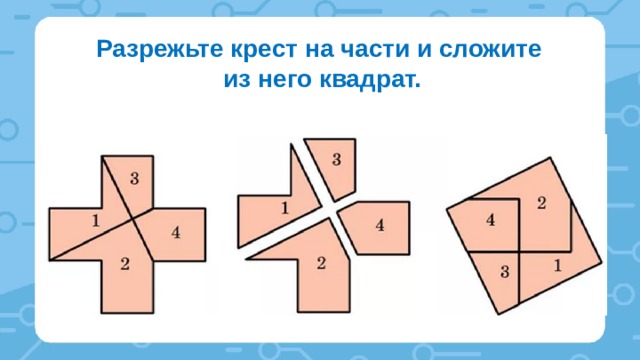
Задача 2.

Задача 3.








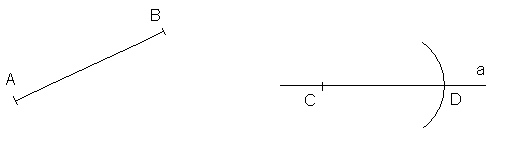

 но: Построение:
но: Построение:

















