
Геометрический метод решения баллистических задач
Баллистическое движение – движение тела в пространстве под действием внешних сил.
Строго говоря, в силу сложности данных задач в рамках школы рассматривается вопрос о движении только под действием силы тяжести. Поэтому далее будем рассматривать вопросы, связанные с движением тел, брошенных под углом к горизонту и движущихся с ускорением свободного падения. Сюда же относится и вертикальное движение, как частный случай. Так как движение происходит только под действием силы тяжести, направленной вертикально вниз (к центру Земли), то данный вид движения можно представить совокупностью равномерного движения по горизонтали и равноускоренного по вертикали с ускорением свободного падения.
Аналитическое решение подобных задач, как правило, приводит к необходимости составления уравнений движений (одно из них квадратное) по двум выбранным осям координат и решению системы уравнений, что в рамках школьной программы часто не является простым решением. Поэтому есть возможность использовать в ряде случаев геометрический подход в решении подобных задач.
Основные формулы равноускоренного движения, которые используются при решении задач, хорошо известны и в векторной форме имеют вид:
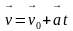
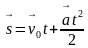


Поскольку правые части данных выражений представляют собой сумму двух векторов (за исключением третьей формулы), то по сути решение сводится к решению задач на нахождение одной из сторон или одного из углов в треугольнике (возможны вариации), т.к. сумму векторов можно найти по правилу треугольника или параллелограмма (кому что нравится). Здесь, как говорится, хороши любые понятия и теоремы из курса геометрии: понятие тригонометрических функций, формулы приведения, теоремы Пифагора, косинусов и синусов, площадь треугольника, площадь параллелограмма, формула Герона, радиусы вписанной и описанной окружностей, понятия медианы, высоты и биссектрисы и так далее.
Рассмотрим каждую формулу в отдельности и постараемся сделать выводы. Для движения под действием силы тяжести здесь и далее заменим ускорение 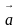 на
на  ,
,
Обозначим α – угол между горизонтом и вектором начальной скорости 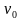

Д
В
анная формула формирует по сути, так называемый,
«треугольник скоростей» 

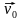

β

α
А


Линия горизонта
Медиана
D


С
Выводы:
Вектор 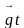 направлен вертикально вниз.
направлен вертикально вниз.
Угол β=900-α
Высота AD есть проекция начальной скорости на горизонтальную ось v0x=v0Cosα
Поделим обе части уравнения 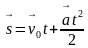 на t. Тогда
на t. Тогда  . Исходя из рисунка, вектор
. Исходя из рисунка, вектор  является медианой в тр-ке ABC.
является медианой в тр-ке ABC.
Если точка бросания и точка падения относительно горизонта находятся на одном уровне (т.е. медиана горизонтальна), то тогда тр-к ABC – равнобедренный, а значит начальная и конечная скорости по модулю равны v=v0 и угол падения равен углу бросания.
Примеры
Задача №1
Тело брошено горизонтально с некоторой высоты со скоростью 6м/с и находилось в полете 0,8с. С какой скоростью тело приземлилось?

Как видим, для простых задач выигрыш в решении невелик.
Треугольник скоростей для данной задачи выглядит так:
V0
gt
V




Линия горизонта
Задача №2
Тело брошено вверх с вертикальной башни под углом α к горизонту со скоростью 9 м/с. Сколько времени тело находилось в полете, если оно приземлилось со скоростью 12 м/с под углом 900- α к горизонту.
Геометрический метод
Треугольник скоростей ниже
V0


gt
v






α
900-α
Из построения видно, что тр-к прямоугольный, а значит по
теореме Пифагора получаем, что v2+v02=(gt)2. Тогда
 =1,5с
=1,5с
Аналитический метод
Пожалуй, он несколько сложнее графического (каждый для себя сравнит сам оба метода в решении данной задачи).
Аналитические методы далее приводить не буду.
Задача №3
Тело, брошенное с поверхности земли со скоростью 10м/с вверх под некоторым углом к горизонту, находилось в полете 1с. Под каким углом брошено тело?
Геометрический метод
Т.к. парабола симметрична относительно своей вершины, то тело поднималось до верхней точки t=0,5с. В верхней точке траектории вектор скорости горизонтален, тогда треугольник скоростей ниже:


V0
gt
v


α

Из рисунка получаем: Sinα=gt/v0=0,5. Тогда α=300.
Задача №4
Тело, брошенное с поверхности земли с некоторой скоростью под некоторым углом к горизонту, упало через 2с. Найдите дальность полета тела, если известно, что вектор начальной скорости перпендикулярен вектору конечной скорости.
Геометрический метод.
Т 





V0
v
gt
s/t
.к. из условия задачи вектор перемещения горизонтален (значит, медиана треугольника тоже горизонтальна, смотрим свойство 4) и треугольник прямоугольный (из условия задачи), то вектор
gt – диаметр описанной окружности.
Тогда  (равны как радиусы окружности) и
(равны как радиусы окружности) и
 =20м.
=20м.
Замечание: Из построения, очевидно, что модуль вектора модуль вектора начальной скорости равен
модулю вектора скорости конечной, что совсем
неочевидно из условия задачи. Из построения
тело брошено под углом 450 к горизонту.
Задача №5
Камень бросают со скоростью v0 под углом φ к горизонту. Через какое время скорость будет составлять угол α с горизонтом?
Геометрический метод.
Построим один из возможных треугольников скоростей.


V0

V
φ


gt

α
Применим теорему синусов для данного треугольника: стороны треугольника относятся друг к другу, как синусы противолежащих им углов.
или , тогда
Очевидно, что данный треугольник построен из предположения, что α, т.е. тело еще не достигло верхней точки траектории. При решении надо учитывать, что после прохождения верхней точки траектории, треугольник скоростей будет несколько иным, а именно



V0
V
φ



gt
α
Задача №6
С одного и того же места с интервалом времени Δt брошены два тела с одной и той же начальной скоростью v0 под углом α к горизонту. Как движется первое тело относительно второго? Почему относительная скорость зависит только от Δt?
Геометрический метод.
Построим два треугольника скоростей на одном рисунке для обоих тел.
gt2
gt1



V0


V2
V1
vотн


α

vотн=v1-v2 (векторная разность!). Из рисунка видно, что vотн направлена вниз и равна gt1-gt2=gΔt. Что и требовалось доказать: относительная скорость зависит только от Δt. Данный треугольник рассматривает случай, когда ни одно тело еще не достигло верхней точки своей траектории. Все остальные случаи предоставляю разобрать читателю самостоятельно.
Задача №7
Из миномета ведут стрельбу по объектам на склоне горы. На каком расстоянии от миномета будут падать мины, если их начальная скорость v0, угол наклона горы α, угол стрельбы по отношению к горизонту β?
Г еометрический метод.
еометрический метод.





α
α
s
v0
β
Построим треугольник скоростей для данного рисунка.



v0
v
gt


s/t



α
β
900- β

Данную задачу можно решить применив теорему синусов.
Ответ:






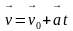
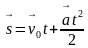


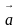 на
на 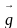 ,
, 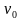



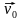






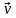
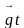 направлен вертикально вниз.
направлен вертикально вниз. . Исходя из рисунка, вектор
. Исходя из рисунка, вектор  является медианой в тр-ке ABC.
является медианой в тр-ке ABC.


















