ГЕОМЕТРИЯ, 7 класс
Тема. Подготовка к контрольной работе по теме «Параллельные прямые. Сумма углов треугольника».
Здравствуйте, дорогие семиклассники!
План работы.
1. Сегодня решаем задачи по теме "Параллельные прямые. Сумма углов треугольника".
2. Посмотрите видеоурок, разберите решение типовых заданий в конспекте урока. Обратите внимание на оформление задачи.
3. Повторите теорию: гл. 3, § 1, § 2; гл. 4, § 1, § 2, § 3.
https://youtu.be/T_krdPDhJvQ?si=4ia0gcq3266e6IKa
Задача №1
Один из острых углов прямоугольного треугольника равен 56°. Найти второй острый угол треугольника.
| 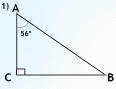 | Дано: ∆ ABC, ∠C=90º. ∠А = 56° Найти: ∠В
|
Решение
Так как сумма острых углов треугольника равна 90º:
∠А + ∠В = 90 º, значит ∠В = 90º – ∠А.
∠В = 90º – 56°= 34º
Ответ: ∠В = 34º
Задача №2
Один из углов, образованных при пересечении двух параллельных прямых секущей, равен 115°. Найти градусные меры остальных образовавшихся углов.
| 
| Дано: прямые a ∥ b, с – секущая. ∠2 = 115° Найти: ∠1, ∠3,∠4, ∠5, ∠6, ∠7, ∠8 |
Решение
∠4 = ∠2 = 115° как вертикальные.
∠6 = ∠4 = 115° внутренние накрест лежащие.
∠8 = ∠6 = 115° как вертикальные.
∠2 + ∠1 = 180° как смежные = ∠1 = 180° - ∠2 = 180° - 115° = 65°
∠3 = ∠1 = 65° как вертикальные.
∠5 = ∠3 = 65° внутренние накрест лежащие.
∠7 = ∠5 = 65° как вертикальные.
Ответ: ∠1= ∠3= ∠5= ∠7= 65°; ∠2= ∠4= ∠6= ∠8= 115°
Задача №3
Найти углы треугольника ΔFPK, если угол ∠F в 3 раза больше угла ∠Р и на 12° меньше угла ∠К.
|  | Дано: ΔFPK; ∠F в 3 раза б. угла ∠Р; ∠F на 12° м. угла ∠К. Найти: ∠F, ∠Р, ∠К
|
Решение
Обозначим ∠P=x°, тогда ∠F=3x°, ∠K=3х+12°.
Так как сумма углов треугольника равна 180°,
∠P+∠F+∠K=180°
x+3x+3x+12°=180°
7x=180°-12°
7x=168°
x=168°: 7
x=24°
∠P=24°, ∠F=3·24=72°, ∠K=72°+12°=84°
Ответ: 24°, 72°, 84°.
Задача №4
Два внутренних угла треугольника относятся как 2:3, а внешний угол при третьей вершине равен 140 градусов. Найти углы треугольника.
|  |
Дано: ΔАВС; ∠А : ∠В = 2 : 3 ∠ВСК – внешний угол при вершине С ∠ВСК = 140°. Найти: углы треугольника ΔАВС
|
Решение
Пусть ∠А = 2х°, ∠В = 3х°.
∠ВСК = ∠А + ∠В по свойству внешнего угла треугольника.
2х +3х = 140
5х = 140
х = 140 : 5
х = 28
Значит:
∠А = 2 ∙ 28 = 56°,
∠В = 3 ∙ 28 = 84°,
∠С = 180 – 140 = 40°,
Ответ: 40°, 56°, 84°
Задача №5
В треугольнике ΔABC угол 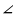 C равен 110°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол ∠AOB.
C равен 110°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол ∠AOB.
| 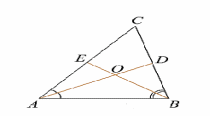 |
Дано: ΔАВС AD, BE — биссектрисы; т.О = AD ∩ BE ; 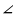 C = 110° C = 110° Найти: ∠AOB.
|
Решение
Сумма углов ΔABС равна 180°:
∠А + ∠В +∠С = 180°, отсюда
∠А + ∠В = 180° – ∠С = 180° –110° = 70°
Рассмотрим ΔAOB.
По теореме о сумме углов треугольника:
∠AOB + ∠ОАB + ∠OBА =180°, отсюда
∠AOB = 180° – (∠ОАB + ∠OBА).
Так как AD, BE — биссектрисы ΔАВС, значит:
∠ОАB = 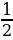 ∠А , ∠OBА =
∠А , ∠OBА = 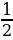 ∠В.
∠В.
∠AOB = 180° – (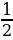 ∠А +
∠А + 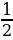 ∠В) = 180° –
∠В) = 180° – 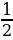 (∠А + ∠В) =
(∠А + ∠В) =
= 180° – 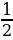 · 70
· 70 = 180° – 35° = 145°
= 180° – 35° = 145°
Ответ: 145°
Контрольная работа №4
Параллельные прямые. Сумма углов треугольника.











 C равен 110°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол ∠AOB.
C равен 110°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол ∠AOB. 
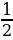 ∠А , ∠OBА =
∠А , ∠OBА =  = 180° – 35° = 145°
= 180° – 35° = 145°










