
Геометрия Многогранников

Цель проекта:
Цель проекта: Изучить многогранники.
Задачи проекта:
- ознакомиться с историей изучения многогранников;
- рассмотреть классификации многогранников;
- научиться моделировать многогранники;
- показать значение многогранников в повседневной жизни.

Понятие многогранника
Многогранник – это тело, граница которого состоит из плоскостей (многоугольников).

УПОМИНАНИЕ
- Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них - пирамиду Хеопса. Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии.

Правильные многогранники
Правильные многогранники известны с древнейших времён. Их орнаментные модели можно найти нарезных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.
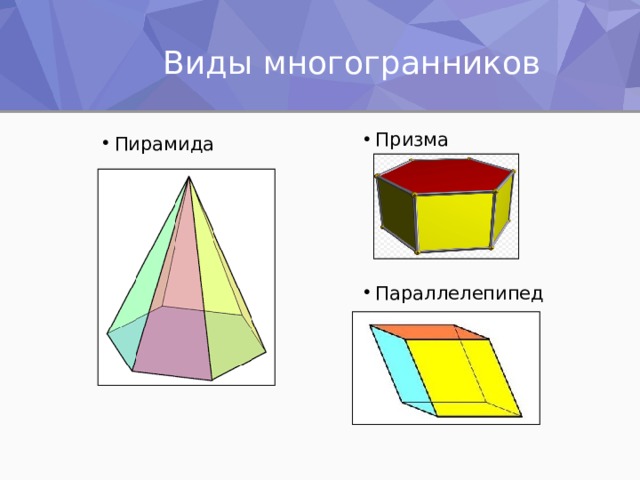
Виды многогранников

Правильный многогранник — это выпуклый многогранник с максимально возможной симметрией
Типы правильных многогранников

Тетра́эдр
(греч. τετραεδρον - четырёхгранник) —многогранник с четырьмя треугольными гранями, в каждой из вершин которого сходятся по 3 грани. У тетраэдра
4 грани,
4 вершины,
6 рёбер .

Окта́эдр
(греч. οκτάεδρον, от греч. οκτа, «восемь» и греч.έδρα - «основание»). Октаэдр -восьмигранник, тело, ограниченное восемью правильными треугольниками.
Октаэдр имеет
8 треугольных граней,
12 рёбер,
6 вершин,
в каждой его вершине сходятся 4 ребра.

Куб или правильный гексаэдр - правильный многогранник, каждая грань которого представляет собой квадрат. Куб или правильный гексаэдр - правильная четырех-угольная призма с равными ребрами, ограниченная шестью квадратами Частный случай параллелепипеда и призмы.

Икоса́эдр
(от греч. εικοσάς — двадцать; -εδρον — грань, лицо, основание) — правильный выпуклый многогранник, двадцати-гранник . Каждая из 20 граней представляет собой равносторонний треугольник. У икосаэдра
30 ребер,
12 вершин,
59 звездчатых форм.
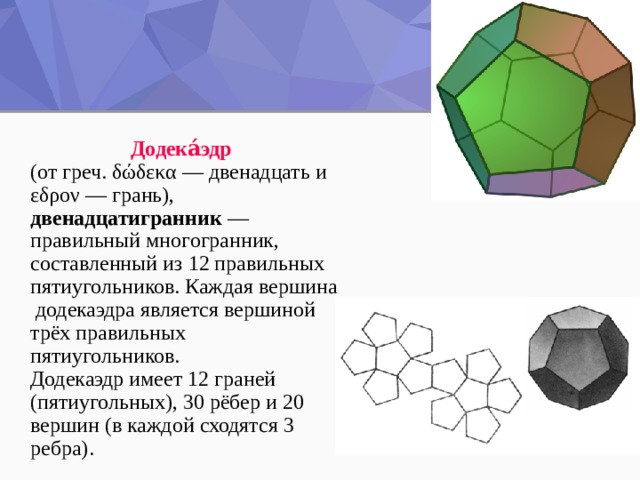
Додека́эдр
(от греч. δώδεκα — двенадцать и εδρον — грань), двенадцатигранник —правильный многогранник, составленный из 12 правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников.
Додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра).
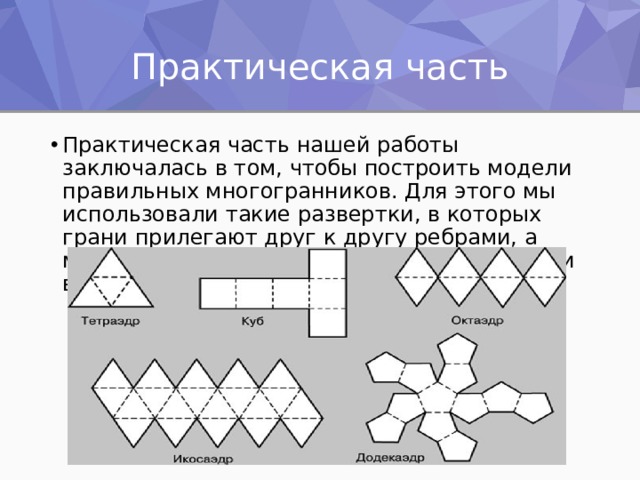
Практическая часть
- Практическая часть нашей работы заключалась в том, чтобы построить модели правильных многогранников. Для этого мы использовали такие развертки, в которых грани прилегают друг к другу ребрами, а модель строится путем загибания развертки вдоль ребер.

Выполнение практической части

Заключение
Таким образом, многогранные формы окружают нас в повседневной жизни повсюду: спичечный коробок, книга, комната, молочные пакеты в форме тетраэдра или параллелепипеда. Почти все сооружения, возведённые человеком, от древнеегипетских пирамид до современных небоскрёбов, имеют форму многогранников.

Спасибо за внимание !











































