Геометрия. Решение треугольников. Презентация к уроку

9 класс

РЕШЕНИЕ ТРЕУГОЛЬНИКОВ

Решение треугольников - нахождение неизвестных сторон и углов треугольника

по известным его углам и сторонам.

Решение прямоугольных треугольников и произвольных треугольников

Сумма углов треугольника равна 180 о

 А +  В +  С = 180 о

А

В

С

Назовите 6 элементов треугольника АВС

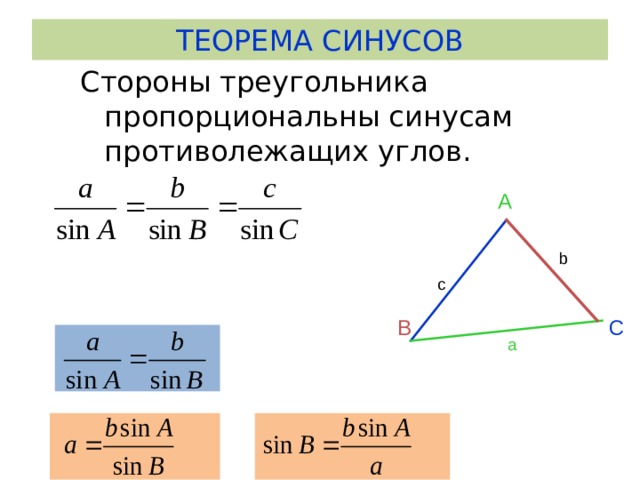
ТЕОРЕМА СИНУСОВ

Стороны треугольника пропорциональны синусам противолежащих углов.

А

b

с

С

В

а

ТЕОРЕМА КОСИНУСОВ

Квадрат стороны треугольника

равен сумме квадратов двух

других сторон минус удвоенное

произведение этих сторон на

косинус угла между ними.

АВ 2 = АС 2 + ВС 2 – 2АС  ВС  cosC

В

a

с

А

С

b

С =

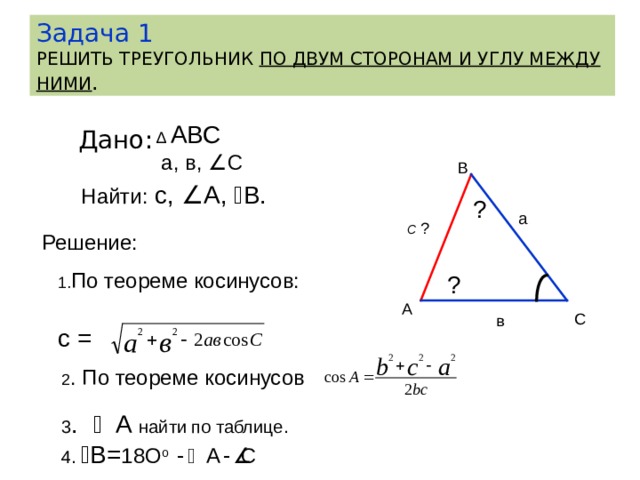
Задача 1 РЕШИТЬ ТРЕУГОЛЬНИК ПО ДВУМ СТОРОНАМ И УГЛУ МЕЖДУ НИМИ .

∆ АВС

Дано:

• Дано:

а, в,  С

В

Найти: с,  А,  В.

?

а

С ?

Решение:

1. По теореме косинусов:

с =

?

А

С

в

2 . По теореме косинусов

3 .  А найти по таблице.

4.  В = 18O о -  А -  C

ЗАДАЧА 2 Решить треугольник по стороне и прилежащим к ней углам .

В

Дано: ∆ A BC ,

a,  В ,  C .

Найти: b , c ,  A.

Решение: 1.  A=180 о -  B -  C .

2. По теореме синусов:

с?

а

?

А

b ?

С

b=

c =

ЗАДАЧА 3 Решить треугольник по трем сторонам .

Дано: ∆ ABC

a, b, c .

Найти:  A ,  B ,  C .

Решение:

По теореме косинусов:

В

?

c

а

?

A

?

b

С

Углы найти с помощью калькулятора или таблиц

 C =18O о

-  А -  B

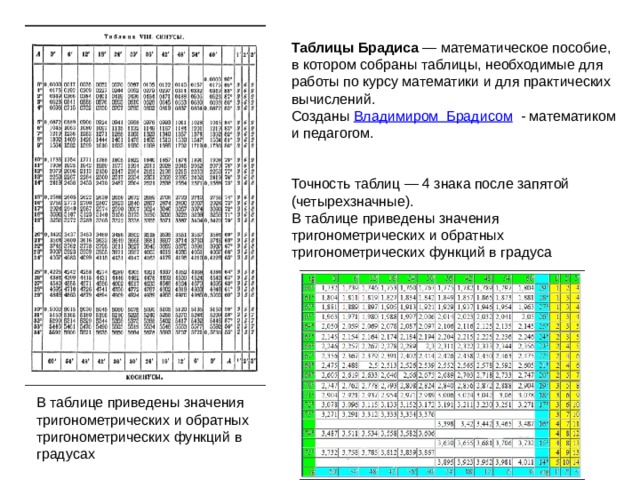
Таблицы Брадиса  — математическое пособие, в котором собраны таблицы, необходимые для работы по курсу математики и для практических вычислений.

Созданы Владимиром Брадисом   - математиком и педагогом.

Точность таблиц — 4 знака после запятой (четырехзначные).

В таблице приведены значения тригонометрических и обратных тригонометрических функций в градуса

В таблице приведены значения тригонометрических и обратных тригонометрических функций в градусах

а 2 +в 2 остроугольный , если с 2 прямоугольный , если с 2 = а 2 +в 2 " width="640"

Это нужно запомнить!

• В треугольнике против большей стороны лежит больший угол, и обратно.
• Косинус большего угла можно найти по формуле из теоремы косинусов.
• Треугольник, у которого с наибольшая сторона, будет

тупоугольный , если с 2 а 2 +в 2

остроугольный , если с 2

прямоугольный , если с 2 = а 2 +в 2

При определении угла треугольника лучше находить его косинус, чем синус. Это связано с тем, что синус не различает смежные углы.

ЗАДАЧА 1. Футбольный мяч находится на расстоянии 23 м от одной штанги ворот и 24 м от другой. Ширина ворот 7 м. Найдите угол попадания мяча в ворота.

7

7

23

24

ЗАДАЧА №1

РЕШЕНИЕ :

24 2 +23 2 -7 2

В

≈

с os A=

23

2 · 23 · 24

7

?

0,9565

≈

А

24

С

 А≈16 ˚58 '

ЗАДАЧА 2. Два геолога находятся на одном берегу реки на расстоянии 300м друг от друга. Один видит дерево на противоположном берегу под углом 38 0 , а другой это же дерево – под углом 67 0 . На каком расстоянии от дерева находятся каждый из них.

ЗАДАЧА №2

РЕШЕНИЕ:

 С =75 ˚

По теореме синусов:

СВ ≈ 284 м

СА ≈192 м

В

?

38 ˚

300

С

67 ˚

?

А

Задача 3. На расстоянии 1500 м от подножия горы находится лыжная база. От подножия горы до вершины 2 км. Какой длины должен быть подъемник, чтобы лыжники могли подниматься на вершину горы прямо от лыжной базы, если угол наклона горы 110 о .

РЕШЕНИЕ ЗАДАЧИ №3.

cos110 ˚=-cos70˚ ≈ -0 ,3420

АВ 2 = 2 2 +1,5 2 -2 · 2 · 1,5 ·cos110 ˚=

≈ 4+2 ,25+6 ·0 ,3420= =8,3021

?

2км

АВ ≈ 2,8813

АВ ≈ 2881м

110 ˚

1500м

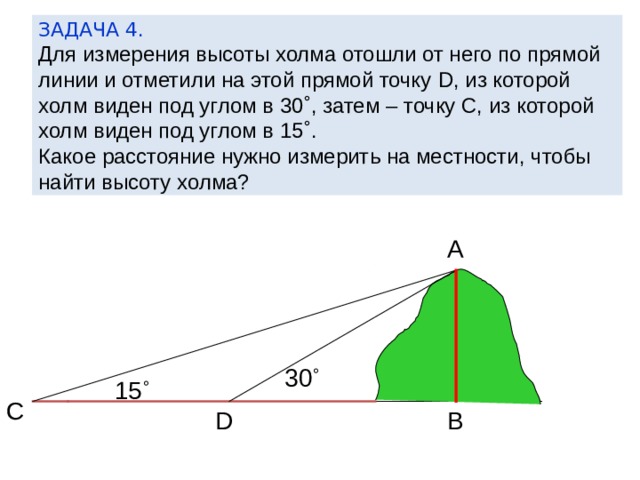
ЗАДАЧА 4. Для измерения высоты холма отошли от него по прямой линии и отметили на этой прямой точку D , из которой холм виден под углом в 30˚, затем – точку С, из которой холм виден под углом в 15˚. Какое расстояние нужно измерить на местности, чтобы найти высоту холма?

А

30 ˚

15 ˚

С

В

D

D