Геометрия 7 класс Признаки равенства треугольников. Прямоугольный треугольник

Павлоградская общеобразовательная школаI-III ступеней №9

2016-2017 учебный год

Урок геометрии в 7-з классе

(в режиме триадной системы обучения)

«Применение свойств и признаков равенства прямоугольных треугольников для решения практических задач »

Тип урока: систематизация и обобщение знаний.

Урок подготовила

Сурина Надежда Александровна,

учитель математики,

высшая категория,

Цели:

Формирующая:

- формировать умения применения свойств и при­знаков равенства прямоугольных треугольников к решению геометрических и практических задач;

- познакомить с историей развития неко­торых математических идей и их влиянием на жизнь современ­ного общества;

Развивающая:

-развивать способность ориентиро­ваться в новых ситуациях, стремление к применению полу­ченных знаний;

Воспитательная:

-воспитывать внимательность и трудолюбие;

-воспитывать уважение к значимости получен­ных знаний;

-воспитывать ответственность за результат своей деятельности.

2017

План урока:

I тридцатка.

1. Проверка д/з(10мин.)

2. Актуализация опорных знаний:

- повторение теоретического материала при работе по готовым чертежам

(фронтально 15 мин.)

-Тест-онлайн. Фронтальная работа и тестирование проводится одновременно.

-индивидуальная работа по карточкам с задачами различной степени сложности.(проводится одновременно с проверкой д/з)

-Подведение итогов, оценивание.

II тридцатка.(изучение свойств биссектрис прямоугольного треугольника, доказывая их по признакам равенства прямоугольных треугольников)

Решение задач на доказательство (работа в парах )

1. Самостоятельная работа по решению задач

с после­дующим объяснением (15 мин).

2.Решение задач из учебника (15 мин).

-Подведение итогов

III тридцатка.

-Решение практических задач

-Решение задач Фалеса.

-Домашнее задание

- Компьютерная презентация о фракталах в современной жизни.

-Подведение итогов урока.

Ход урока

Сегодня один из итоговых уроков по теме «Признаки равенства треугольников. Прямоугольный треугольник »(тема записывается в тетрадях)

Назовите ключевое слово в названии темы. (ученики называют слово-треугольник)

Сегодня мы будем решать задачи по теме и

кроме этого, мы должны определить сферы практического использования знаний по данной теме.

А при подведении итога урока мы с вами опять должны ответить на основополагающий вопрос урока: Чем удивителен треугольник?

1.Проверка д/з

- Доказать теорему:

Катет прямоугольного треугольника, лежащий против угла 30⁰, равен половине гипотенузы;(модель 2 прямоугольных треугольников)

- комментируют решения д/з№447 (метод решения задач на деление величины в заданном отношении и использование свойств углов прямоугольного треугольника)

Что является важным при решении задач? (Знание определений и теорем)

-одна половина класса (8 учащихся) выполняют тестовые задания на компьюторе по проверке теории, (15 минут)

-другая- решает задания по готовым чертежам.

- два ученика решают задачи различной степени сложности в рабочих тетрадях

(№446-9б, №463-11б)

- Работа по готовым чертежам:

1) Найдите пары равных треугольников и объясните их ра­венство.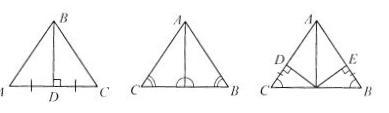

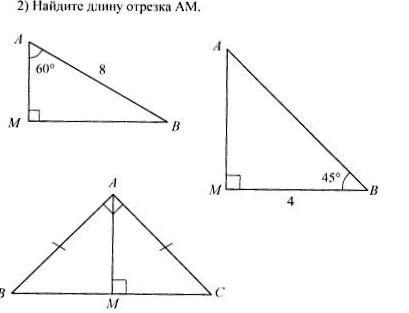
ВС=24см.

3) Найдите угол а.

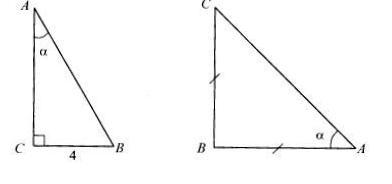
АВ=8

(№468-фронтально решать по рисунку на доске, если будет время))

3.Тест онлайн по теме « Свойства прямоугольного треугольника»

Подведение итогов, оценивание.

Вторая тридцатка.

Формирование умений решать задачи на доказательство.

Доказательство свойств биссектрис прямоугольного треугольника ,используя признаки равенства прямоугольного треугольника)

1. Самостоятельная работа (работа в группах).

На доске и в тетрадях выполняется рисунок: угол и в нем проведена биссектриса.

I. Доказать, что каждая точка биссектрисы угла равноудале­на от его сторон.

2. Доказать, что каждая точка, равноудаленная от сторон уг­ла, лежит на его биссектрисе.

2. Работа по учебнику (работа в парах, задачи решаются последовательно и обсуждаются фронтально)

№449 Доказать ,что биссектрисы острых углов прямоугольного треугольника пересекаются под углом 45⁰.

№463 (устно)Могут ли биссектрисы двух углов прямоугольного треугольника пересекаться под углом 40⁰?(нет, т.к. это не биссектрисы острых углов, а значит это биссектрисы прямого угла и одного из острых. Данный угол является внешним для треугольника, ограниченного этими биссектрисами и одним из катетов, и равен сумме двух внутренних углов треугольника, не смежных с ним, а один из слагаемых уже равен 45⁰)

№ 462(самостоятельно в рабочих тетрадях)Найдите углы прямоугольного треугольника, если биссектрисы двух его углов пересекаются под углом 70⁰.(ответ: 50⁰ и 40 ⁰ и можно не обсуждать)

Подведение итогов

Третья тридцатка

1. Решение практических задач.

1. Жители трех домов, расположенных в вершинах равно­бедренного прямоугольного треугольника, хотят выкопать об­щий колодец с таким расчетом, чтобы он был одинаково удален от всех трех домов. В каком месте надо копать?

Ответ: Копать надо в точке О.

2. Задачи Фалеса:

а) Египтяне задали Фалесу трудную задачу: найти высоту одной из громадных пирамид. Фалес нашел для этой задачи простое и красивое решение. Он воткнул в землю вертикально длинную палку и сказал: «Когда тень от этой палки будет той же длины, что и сама палка, тень от пирамиды будет иметь ту же длину, что и высота пирамиды».

б) Еще одно из свойств прямоугольного треугольника, дока­занное Фалесом. Нарисуем прямоугольный треугольник АВС и разделим его гипотенузу АС точкой О пополам. Как вы думаете, какой отрезок длиннее:

АО или ОВ или ОС? То есть куда ближе идти из середины гипотенузы - к острому углу или к прямому?

Р е ш е н и е .

Достроим треугольник АВС до прямоугольника АDВС. АВ = СД и точ­ка О - середина каждой из них. Следовательно, АО = ОB = ОС.(для решения задачи иметь модели 4 равных прямоугольных треугольника)

Теорема: Медиана, проведенная к гипотенузе , равна ее половине.

(записать в рабочую тетрадь)

1. Подведение итогов(главные слова-треугольник и биссектриса .Чему научились на уроке? Чем удивителен треугольник?)

оценивание, задание на дом.

1. Домашнее задание:-пройти тесты онлайн (на сайте учителя для самооценки)-Презентация о Фалесе(10 слайдов)-домашняя к/р вариант 1 стр.127 учебника геометрии 7

2. «Рано или поздно всякая правильная математическая идея находит применение в том или ином деле».А.Н.Крылов

Компьютерная презентация о фрактальных структурах. (10 мин.)