Графическое решение систем неравенств с двумя переменными

Системы неравенств

с двумя переменными

К учебнику Ю.Н.Макарычева

Алгебра, 9 класс, Глава III §

Автор: Софронова Наталия Андреевна,

учитель математики высшей категории

МОУ «Упшинская основная общеобразовательная школа»

Оршанского района Республики Марий Эл

Решение системы неравенств

с двумя переменными

Решением системы неравенств с двумя переменными называется пара значений этих переменных, являющаяся как решением первого неравенства, так и второго неравенства системы.

(1; 2) – решение ?

( 2; 1) – решение ?

(1; 2) – решение

( 2; 1) –не решение

Изображение множества решений неравенства с двумя переменными на координатной плоскости

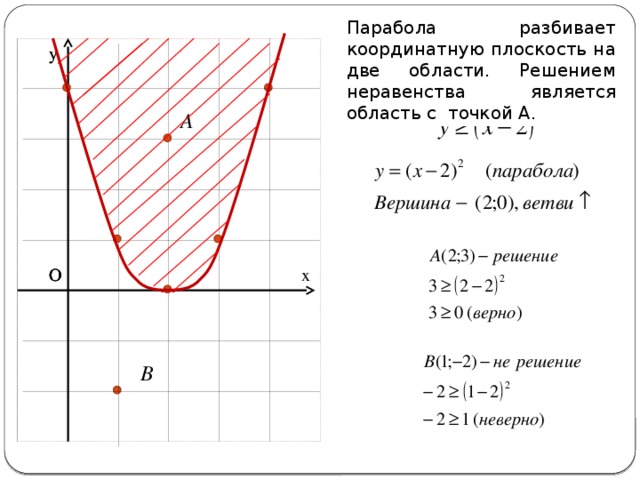
Парабола разбивает координатную плоскость на две области. Решением неравенства является область с точкой А.

у

у

А

О

О

О

х

В

Изображение множества решений системы неравенств с двумя переменными на координатной плоскости

Множеством решений системы неравенств с двумя переменными является пересечение множеств решений неравенств, входящих в систему. На координатной плоскости множество решений системы неравенств изображается множеством точек, являющихся общей частью множеств, представляющих собой решения каждого неравенства системы.

х = 2

у

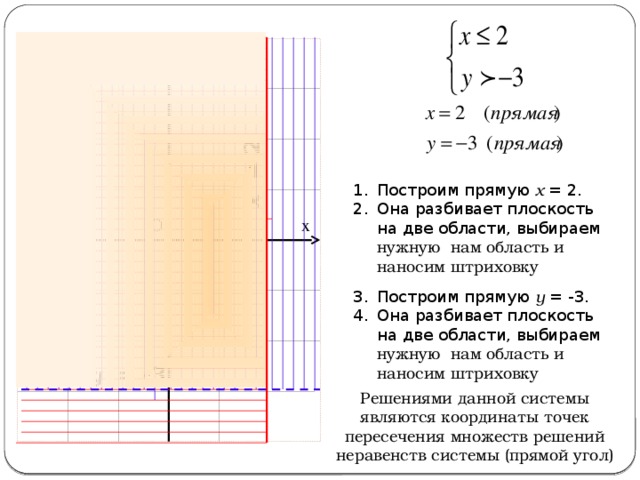
• Построим прямую х = 2.
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

О

х

• Построим прямую у = -3.
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

у = -3

Решениями данной системы являются координаты точек пересечения множеств решений неравенств системы (прямой угол)

у

х

у

0

3

2

0

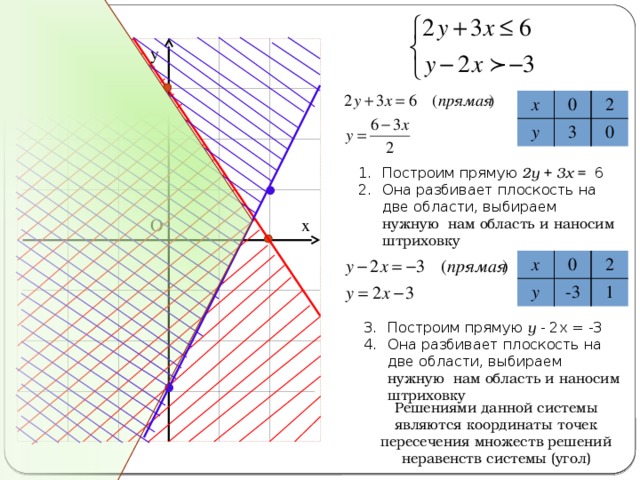
• Построим прямую 2у + 3х = 6
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

О

х

х

у

0

2

-3

1

• Построим прямую у - 2х = -3
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются координаты точек пересечения множеств решений неравенств системы (угол)

у

х

у

0

1

1

3

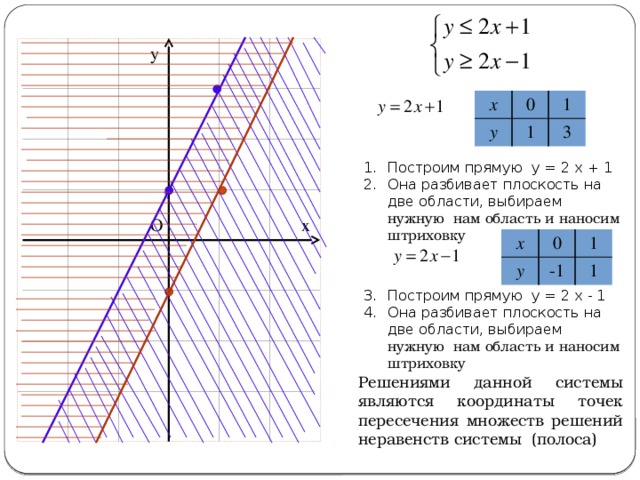
• Построим прямую у = 2 х + 1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

О

х

х

у

0

1

-1

1

• Построим прямую у = 2 х - 1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются координаты точек пересечения множеств решений неравенств системы (полоса)

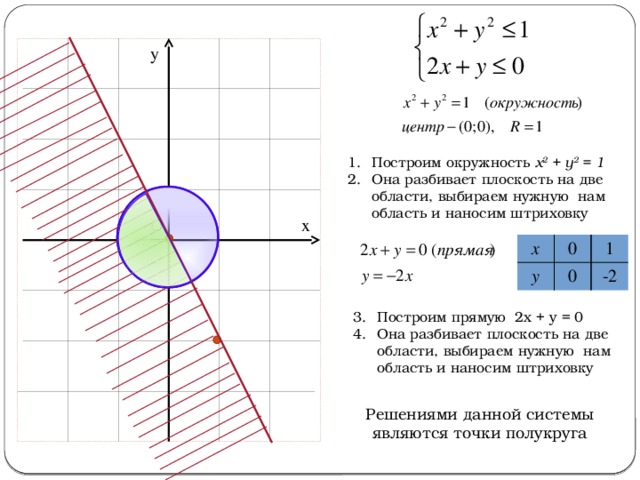
у

• Построим окружность х 2 + у 2 = 1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

х

О

х

у

0

1

0

-2

• Построим прямую 2х + у = 0
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются точки полукруга

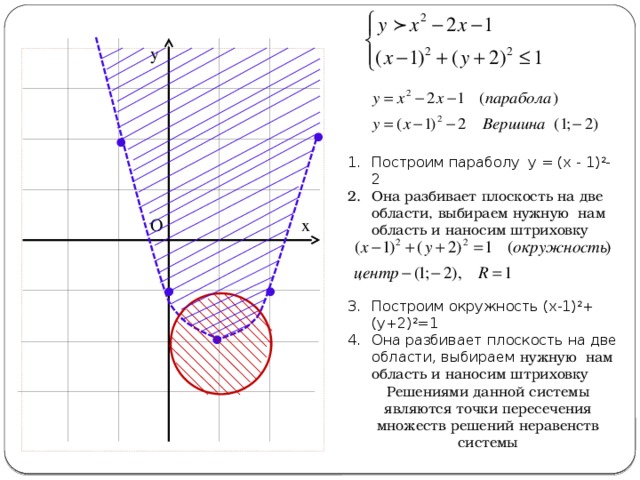
у

• Построим параболу у = (х - 1) 2 -2
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

х

О

• Построим окружность (х-1) 2 +(у+2) 2 =1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются точки пересечения множеств решений неравенств системы

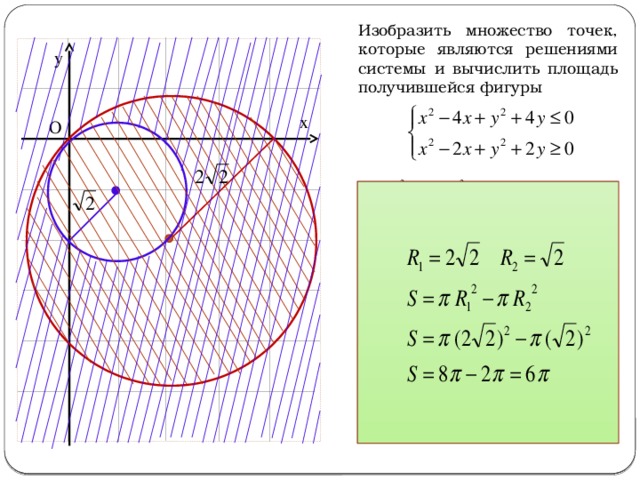
Изобразить множество точек, которые являются решениями системы и вычислить площадь получившейся фигуры

у

х

О

у

О

х