Интегрированный урок математики и информатики в 9-м классе по теме: "Построение и преобразование графиков квадратичной функции" Составила: Федорова Оксана Юрьевна, учитель математики и информатики, школа №3 Тип урока: урок усвоения новых знаний.
Оборудование и материалы: 10 ПК (установлена операционная система Windows 7, Microsoft Excel).
Подготовка к уроку: На рабочем столе каждого компьютера поместить файл «Графики», распечатать задание для практической работы, тест, подготовить презентацию об ученых занимавшихся функцией, презентацию о академике С.Л.Соболеве.
Цели урока:
Образовательные:
экспериментальным путем (с использованием ПК) получить алгоритмы построения графиков функций видов y=f(x+t), y=f(x)+m,y=f(x+t)+m, если известен график функции y=f(x);
научиться применять полученные алгоритмы к построению графиков функций (без использования ПК);
закрепление умений работать с операционной системой Windows, работа с электронными таблицами.
Развивающие:
формирование умений сравнивать, обобщать изучаемые факты;
развитие у учащихся самостоятельности в мышлении и учебной деятельности;
развитие эмоций учащихся путем привлечения наглядности и средств ТСО (компьютер).
Воспитательные:
воспитание коллективизма и ответственности за общую работу;
воспитание взаимопомощи;
воспитание аккуратности (при выполнении построения графиков функций).
чувство патриотизма и уважение к Родине.
ХОД УРОКА
1. Организационный момент.
Н.Е.Жуковский сказал «В математике есть своя красота, как в живописи и поэзии» сегодня на уроке мы научимся очень красивому методу построения графиков квадратичной функции.
2. Актуализация знаний.
Презентация: «Ученые, занимавшиеся функцией. Русские ученые»
Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами.
Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт; они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение: неизвестных - последними буквами латинского алфавита - x, y, z, известных - начальными буквами того же алфавита - a, b, c, ... и т.д. Под каждой буквой стало возможным понимать не только конкретные данные, но и многие другие; в математику пришла идея изменения. Тем самым появилась возможность записывать общие формулы.
Само слово «функция» (от латинского functio -совершение, выполнение) впервые было употреблено немецким математиком Лейбницем в 1673г. в письме к Гюйгенсу (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), в печати ввел с 1694 года.
Поговорим о русских ученых внесших вклад в развитие понятия функция. Это Николай Иванович Лобачевский. Заслуги Лобачевского в других областях математики не так велики, как его геометрическое дело. Но его крупный математический талант проявился и в других исследованиях, например, в исследованиях о сходимости строк. В особенности, указанную им с полной определенностью необходимость отличать постепенность (непрерывность) и непрерывность (дифференцируемость). В этом вопросе Лобачевский также опередил своих современников на несколько десятилетий. Учебник алгебры Лобачевского, изданный им в 1834г. под заглавием: "Алгебра или вычисление конечных" - отличается от других учебников алгебры, не только в России, но и за границей, систематичностью расположения, строгостью изложения основных понятий и замечательной полнотой.
3. Темы, цели урока. Организация восприятия и осознания нового материала.
- В 8 классе мы познакомились с функцией у=х2.
- А являются ли квадратичными следующие функции, записанные на доске?
у = (х+3)2 у = х2+3 у =- (х-3)2+4
- Знаем ли мы способ построения графиков таких функций? (Да, по контрольным точкам).
- Но построение таких графиков по точкам может занять очень много времени, а мы сегодня научимся строить такие графики быстро.
Итак, тема урока: “Преобразование графиков квадратичной функции” и мы на уроке должны экспериментальным путем получить алгоритм для построения графиков квадратичных функций подобных видов.
Сегодня на уроке вам будет помогать компьютер, и поэтому, еще одной задачей нашего урока будет отработка навыков работы с операционной системой Windows XP и электронными таблицами.
4. Объяснение нового материала. Практическая работа.
- Мы знаем, что компьютер – инструмент, который работает с конкретными математическими моделями, давайте и мы выделим математическую модель квадратичной функции
у=а(х+m)2 + n
Задание 1. На рабочем столе лежит файл электронных таблиц «Графики». На диске С: создайте папку «Практическая работа по математике» и переместите этот файл в созданную папку (Как перейти на диск С:? Как создать папку? Как переместить файл в эту папку?)
С помощью электронных таблиц мы будем строить графики функций, а ваша задача пронаблюдать за последовательностью построения графиков и попробовать сформулировать алгоритм построения графиков функций данной модели.
Инструкция по работе с программой:
Перед вами 3 столбца чисел
блок A10:A30 – это значение переменной х
блок B10:B30 – это значение функции у=х2
блок C10:C30 – это значение функции у=а(х+m)2 + n.
При вводе в ячейки E4, E5, E6 чисел автоматически пересчитываются значения функции в блоке C10:C30. Такое достигается, если мы используем, какие ссылки при составлении формул?
– Правильно, абсолютные ссылки.
По блокам B10:B30 и C10:C30 построены диаграммы в виде линейных графиков. Мы видим сразу два графика, синий график это график функции у=х2 будет оставаться на месте, а красный график, это график функции у=а(х+m)2 + n будет сдвигаться в зависимости от чисел которые вы введете в ячейки E4, E5, E6.
У вас на столах лежит задание для практической работы, вы должны параметрам a,m,n придать различные значения и сделать вывод куда будет сдвигаться график. В конце работы попробуйте составить алгоритм построения графика у=а(х+m)2 + n.
(Учащиеся работают в группах за одним компьютером по 2 человека).

Практическая работа по теме:
Преобразование графика квадратичной функции f(x)=x².
Задание: Построить график g(x)=a(x+m)²+n и описать преобразование.
| a | m | n | Формула функции | Преобразование графика. |
| a=1 | m=5 | n=0 | g(x)= | График функции g(x) получается из графикаf(x) в результате _________ вдоль оси_______ на ___ единиц. |
| a=1 | m=-5 | n=0 | g(x)= | График функции g(x) получается из графика f(x) в результате___________ вдоль оси_________ |
| a=1 | m=0 | n=20 | g(x)= | График функции g(x) получается из графика f(x) в результате ________ вдоль оси_________ |
| a=1 | m=0 | n=-60 | g(x)= | График функции g(x) получается из графика f(x) в результате__________ вдоль оси ________ |
| a=1 | m=5 | n=50 | g(x)= | График функции g(x) получается из графика f(x) в результате___________ вдоль оси ____________ |
| a=1 | m=-2 | n=-40 | g(x)= | График функции g(x) получается из графика f(x) в результате____________ вдоль оси ____________ |
| a=1 | m=3 | n=-30 | g(x)= | График функции g(x) получается из графика f(x) в результате___________ вдоль оси___________ |
| a=-1 | m=3 | n=0 | g(x)= | График функции g(x) получается из графика f(x) в результате___________ |
| a=-1 | m=0 | n=-30 | g(x)= | График функции g(x) получается из графика f(x) в результате___________ |
| a=-1 | m=-1 | n=40 | g(x)= | График функции g(x) получается из графика f(x) в результате___________ |
| a=-1 | m=3 | n=-20 | g(x)= | График функции g(x) получается из графика f(x) в результате___________ |
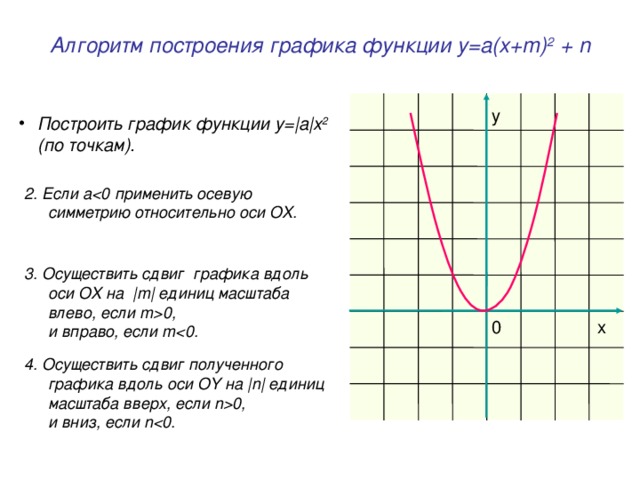
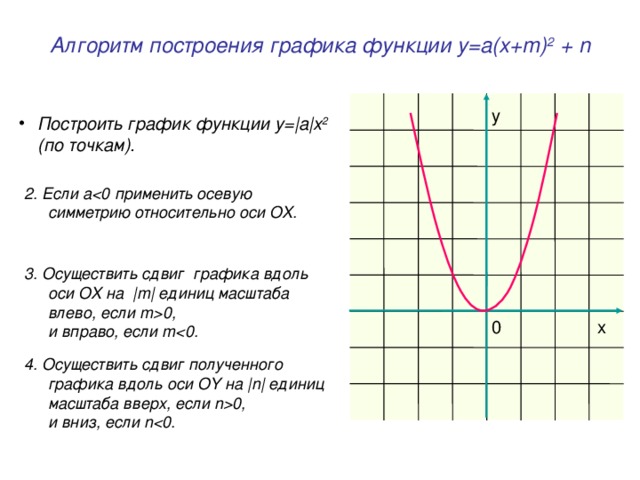
Алгоритм разбирается и показывается на слайде.
Построить график функции у=|a|x2 (по точкам).
Eсли аOX.
Осуществить сдвиг графика вдоль оси OX
на |m| единиц масштаба влево, если m0,
и вправо, если m
Осуществить сдвиг полученного графика вдоль оси OY
на |n| единиц масштаба вверх, если n0,
и вниз, если n
- Итак, мы получили алгоритмы для построения графиков квадратичных функций. Как вы считаете, будут ли полезны эти алгоритмы в нашей работе, облегчат ли они нам работу?
5. Первичное закрепление полученных знаний.
Задание . С помощью данного алгоритма в одной системе координат постройте график функции.
у =(х-2)2+1
6. Проверка усвоения знаний.
- Сейчас вам предстоит выполнить небольшой тест, результаты которого покажут, насколько вы усвоили материал сегодняшнего урока и определят задачи следующих уроков.
Тест
Определите, какая графическая модель, соответствует каждой из данных функций.
Буквы обозначающие графики, запишите рядом с формулами.
| Б
| Е y
|
| Л
| С
|
| В |
|
|
|
| y

|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
| 2
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| | 
|
| -3
|
| 0
|
|
|
| x
|
|
|
|
| О
|
| О
| К
|
| y = x2 - 2 | y = (x-2)2 | y = (x+2)2-3 | y = -(x-2)2+3 | y = x2 | y = - x2+2 | y = (x+3)2+2 |
|
|
|
|
|
|
|
|
Дети получают фамилию Сергей Львовича Соболева.
Выступление ученика о С.Л.Соболеве. Учитель демонстрирует презентацию об академике Соболеве.
Соболев Сергей Львович (род. в 1908г.)
Советский математик. Основные труды по теории уравнений с частными производными, математической физике, функциональному анализу и вычислительной математике. Предложил новый метод решения гиперболических уравнений с частными производными, совместно со Смирновым В.И. разработал метод функционально-инвариантных решений для динамических колебаний слоистых сред. Им начато систематическое применения функционального анализа в теории уравнений с частными производными. Им же введен класс функциональных пространств и исследовано соотношение вложения для пространств. Ввел понятие обобщенного решения уравнения с частными производными и дал первое (1935) строгое определение обобщенной функции; с помощью этих понятий рассмотрел некоторые краевые задачи для уравнения с частными производными. В области вычислительной математики Соболев ввел понятие замыкаемых вычислительных алгоритмов, дал точную оценку норм погрешности кубатурных формул.
7. Итог урока. Домашнее задание.
- Ребята, чему вы сегодня научились на уроке?
- Как вы считаете, полученные нами алгоритмы будут справедливы для построения графиков линейной функции и графиков функции обратная пропорциональность? Попробуйте проверить это дома сами, а мы разберемся с этим на следующем уроке.
- Для того чтобы вы дома потренировались использовать алгоритмы построения графиков, запишите себе следующее домашнее задание: построить графики функций
y=2x2+4; y=2(x+3)2-5; y=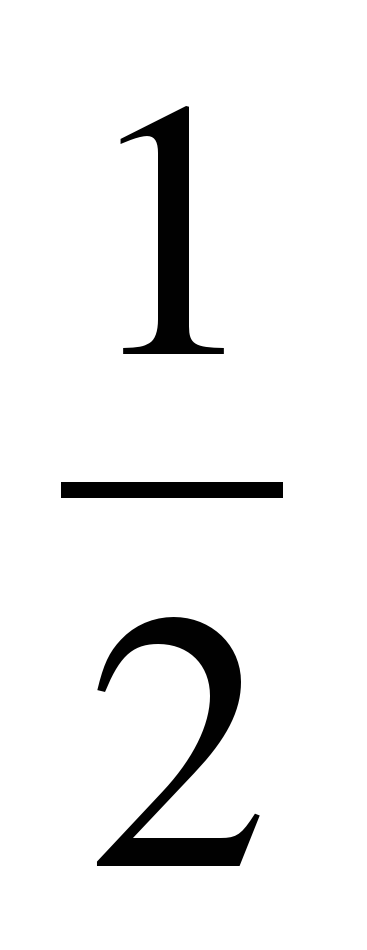 (x-6)2; y= –
(x-6)2; y= –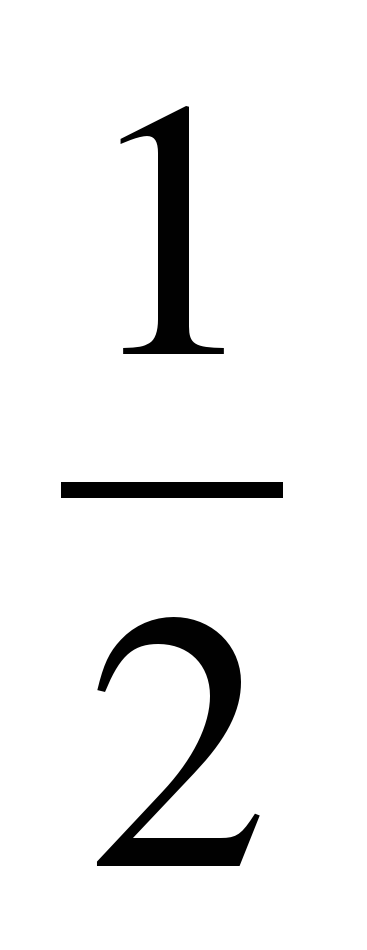 (x-3)2+4.
(x-3)2+4.















 0, и вправо, если m x 0 4. Осуществить сдвиг полученного графика вдоль оси OY на |n| единиц масштаба вверх, если n0, и вниз, если n" width="640"
0, и вправо, если m x 0 4. Осуществить сдвиг полученного графика вдоль оси OY на |n| единиц масштаба вверх, если n0, и вниз, если n" width="640"
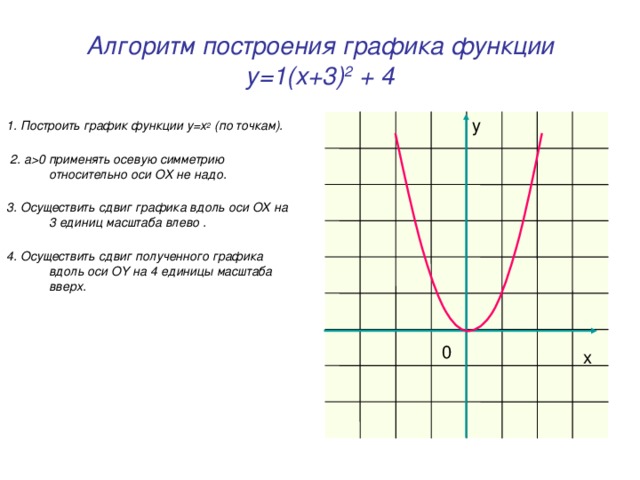
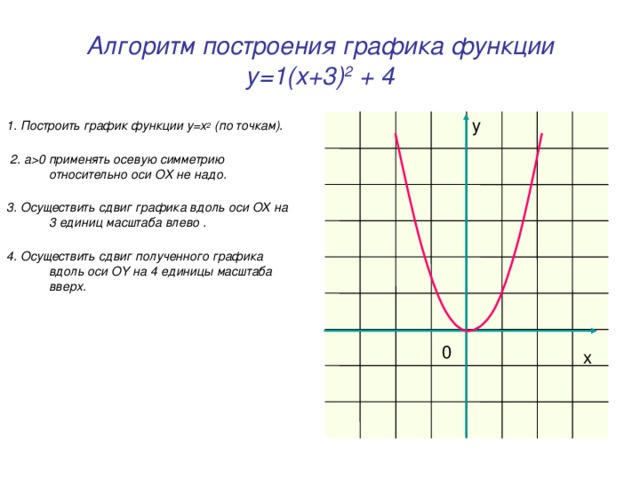 0 применять осевую симметрию относительно оси OX не надо. 3. Осуществить сдвиг графика вдоль оси OX на 3 единиц масштаба влево . 4. Осуществить сдвиг полученного графика вдоль оси OY на 4 единицы масштаба вверх. y 0 x" width="640"
0 применять осевую симметрию относительно оси OX не надо. 3. Осуществить сдвиг графика вдоль оси OX на 3 единиц масштаба влево . 4. Осуществить сдвиг полученного графика вдоль оси OY на 4 единицы масштаба вверх. y 0 x" width="640"
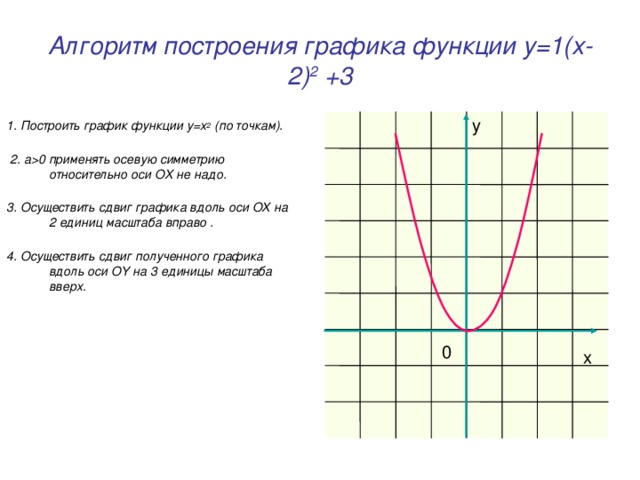
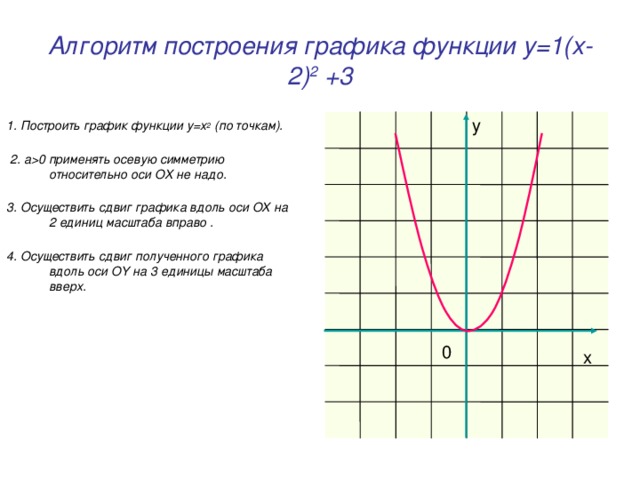 0 применять осевую симметрию относительно оси OX не надо. 3. Осуществить сдвиг графика вдоль оси OX на 2 единиц масштаба вправо . 4. Осуществить сдвиг полученного графика вдоль оси OY на 3 единицы масштаба вверх. y 0 x" width="640"
0 применять осевую симметрию относительно оси OX не надо. 3. Осуществить сдвиг графика вдоль оси OX на 2 единиц масштаба вправо . 4. Осуществить сдвиг полученного графика вдоль оси OY на 3 единицы масштаба вверх. y 0 x" width="640"
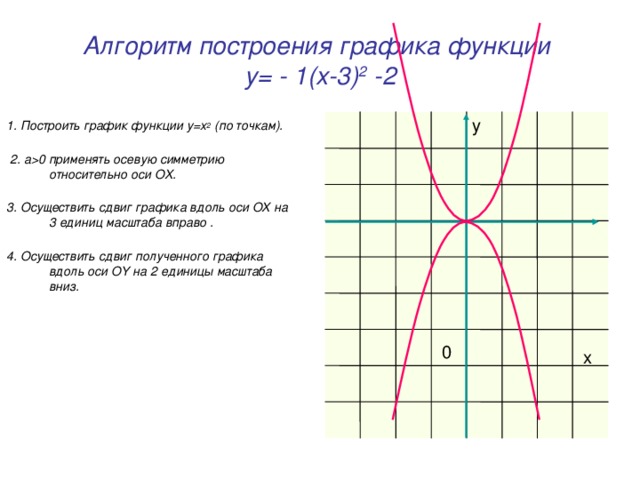
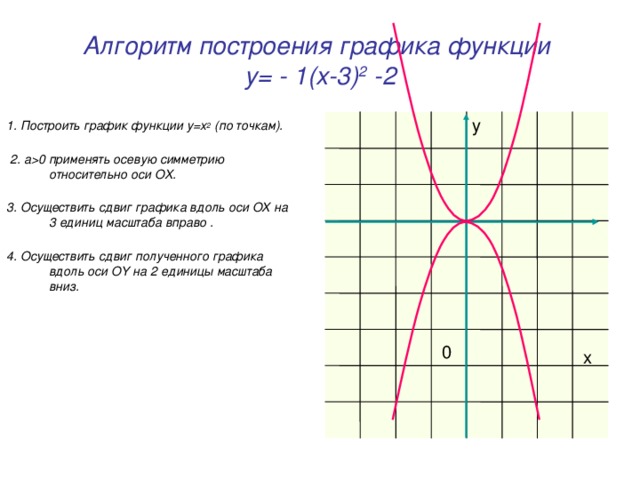 0 применять осевую симметрию относительно оси OX. 3. Осуществить сдвиг графика вдоль оси OX на 3 единиц масштаба вправо . 4. Осуществить сдвиг полученного графика вдоль оси OY на 2 единицы масштаба вниз. y 0 x" width="640"
0 применять осевую симметрию относительно оси OX. 3. Осуществить сдвиг графика вдоль оси OX на 3 единиц масштаба вправо . 4. Осуществить сдвиг полученного графика вдоль оси OY на 2 единицы масштаба вниз. y 0 x" width="640"
 0, и вправо, если m x 0 4. Осуществить сдвиг полученного графика вдоль оси OY на |n| единиц масштаба вверх, если n0, и вниз, если n" width="640"
0, и вправо, если m x 0 4. Осуществить сдвиг полученного графика вдоль оси OY на |n| единиц масштаба вверх, если n0, и вниз, если n" width="640"
 0 применять осевую симметрию относительно оси OX не надо. 3. Осуществить сдвиг графика вдоль оси OX на 3 единиц масштаба влево . 4. Осуществить сдвиг полученного графика вдоль оси OY на 4 единицы масштаба вверх. y 0 x" width="640"
0 применять осевую симметрию относительно оси OX не надо. 3. Осуществить сдвиг графика вдоль оси OX на 3 единиц масштаба влево . 4. Осуществить сдвиг полученного графика вдоль оси OY на 4 единицы масштаба вверх. y 0 x" width="640"
 0 применять осевую симметрию относительно оси OX не надо. 3. Осуществить сдвиг графика вдоль оси OX на 2 единиц масштаба вправо . 4. Осуществить сдвиг полученного графика вдоль оси OY на 3 единицы масштаба вверх. y 0 x" width="640"
0 применять осевую симметрию относительно оси OX не надо. 3. Осуществить сдвиг графика вдоль оси OX на 2 единиц масштаба вправо . 4. Осуществить сдвиг полученного графика вдоль оси OY на 3 единицы масштаба вверх. y 0 x" width="640"
 0 применять осевую симметрию относительно оси OX. 3. Осуществить сдвиг графика вдоль оси OX на 3 единиц масштаба вправо . 4. Осуществить сдвиг полученного графика вдоль оси OY на 2 единицы масштаба вниз. y 0 x" width="640"
0 применять осевую симметрию относительно оси OX. 3. Осуществить сдвиг графика вдоль оси OX на 3 единиц масштаба вправо . 4. Осуществить сдвиг полученного графика вдоль оси OY на 2 единицы масштаба вниз. y 0 x" width="640"





















Электронная тетрадь по информатике 8...
Информатика 8 класс ФГОС
Информатика 10 класс (Россия)
Информационная безопасность
Электронная тетрадь по информатике 7...
Информатика и ИКТ 11 класс (к учебнику...
Электронная тетрадь по информатике 6...
Информатика 3 класс
© 2016, Федорова Оксана Юрьевна 2112 19
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы