УПРАВЛЕНИЕ АЛТАЙСКОГО КРАЯ ПО ОБРАЗОВАНИЮ И ДЕЛАМ МОЛОДЕЖИ
КГБОУ «АЛТАЙСКИЙ КРАЕВОЙ ИНСТИТУТ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ РАБОТНИКОВ ОБРАЗОВАНИЯ»
АЛТАЙСКИЙ КРАЕВОЙ ИНФОРМАЦИОННО-АНАЛИТИЧЕСКИЙ ЦЕНТР
ГВЭ по математике
(9 класс) – 2016
В издании представлены результаты ГВЭ (9 класс) по математике, прошедшего в Алтайском крае в 2016 году.
Подготовленный КГБОУ «Алтайский краевой институт повышения квалификации работников образования» анализ результатов основного государственного экзамена по математике выпускников 9 классов в Алтайском крае ориентирован на практических работников системы образования, и, прежде всего, учителей математики общеобразовательных организаций.
Содержание включает не только количественное описание результатов ГВЭ по математике выпускников 9 классов Алтайского края, но также подробный качественный анализ выполнения школьниками экзаменационных заданий, допущенных ими типичных ошибок, недочетов.
Публикуемые сведения могут быть востребованы работниками органов управления образованием муниципального и краевого уровня, а также научными работниками, занимающимися исследованием региональных образовательных систем.
Статистическая информация предоставлена Региональным центром обработки информации Единого государственного экзамена в Алтайском крае.
© КГБОУ АКИПКРО,
КГБУО «АКИАЦ», 2016
Государственный выпускной экзамен для учащихся 9 классов, освоивших образовательные программы основного общего образования, проводился в соответствии с Порядком проведения государственной итоговой аттестации по образовательным программам основного общего образования. Этот Порядок был утвержден приказом Минобрнауки России от 25.12.2013 № 1394, зарегистрирован Минюстом России 03.02.2014, регистрационный номер № 31206, в редакции приказа Минобрнауки России от 16.01.2015 № 10, зарегистрирован Минюстом России 27.01.2015, регистрационный № 35731.
Подробные сведения об экзамене даны в Методическом письме, в котором говорится о проведении государственной итоговой аттестации по образовательным программам основного общего образования по математике в форме государственного выпускного экзамена (письменная и устная форма) (письмо Рособрнадзора от 26.02.2015 № 02 - 61). Указанное письмо размещено на сайте ФГБНУ «ФИПИ».
В соответствии с этим Порядком экзамен по математике является обязательным.
Аттестация в форме ГВЭ (9 кл.) проводилась для определенных категорий обучающихся, а именно:
выпускников 9-х классов специальных учебно-воспитательных учреждений закрытого типа, а также учреждений уголовно-исполнительной системы;
обучающиеся в образовательных организациях, расположенных за пределами Российской Федерации, и реализующих имеющие государственную аккредитацию образовательные программы основного общего образования, и загранучреждениях;
обучающиеся с ОВЗ, детей – инвалидов и инвалидов, освоивших образовательные программы основного общего образования;
обучающихся, освоивших в 2014 – 2016 годах образовательные программы основного общего образования в образовательных организациях, расположенных на территориях Республики Крым и города федерального значения Севастополя.
Исходя из положений Закона № 181- ФЗ и Семейного кодекса РФ, под ребенком-инвалидом понимается лицо, не достигшее 18 лет, которое имеет нарушение здоровья со стойким расстройством функций организма, обусловленное заболеваниями, последствиями травм или дефектами, приводящее к ограничению жизнедеятельности и вызывающее необходимость социальной защиты.
Ограничение жизнедеятельности в данном случае – полная или частичная утрата способности или возможности самостоятельно обслуживать себя, передвигаться, ориентироваться, общаться, контролировать свое поведение, обучаться и заниматься трудовой деятельностью.
В зависимости от степени расстройства функций организма и ограничения жизнедеятельности лицам, признанным инвалидами, устанавливается группа инвалидности, а лицам в возрасте до 18 лет устанавливается категория "ребенок-инвалид".
Что касается детей с ограниченными возможностями здоровья, то к данной категории относятся дети, имеющие недостатки в физическом и (или) психическом развитии, препятствующие получению образования без создания специальных условий.
Письменный экзамен ГВЭ – 9 по математике проводился в нескольких форматах в целях учета возможностей разных категорий его участников: участников без ОВЗ и участников с ОВЗ.
Участники ГВЭ без ОВЗ и с ОВЗ (за исключением участников с задержкой психического развития) сдавали экзамен по экзаменационным материалам, номер которых был маркирован буквой «А».
Участники ГВЭ с задержкой психического развития могли сдавать экзамен по экзаменационным материалам, номер которых был маркирован буквой «К».
ГВЭ – 9 в устной форме проходил для следующих участников с ОВЗ: слепые, слабовидящие и поздноослепшие обучающиеся, не владеющие рельефно – точечным шрифтом Брайля, обучающиеся с нарушением опорно – двигательного аппарата.
Каждый вариант экзаменационной работы, маркированного буквой «А»,
Содержал 12 заданий, из которых 10 заданий с кратким ответом, в которых необходимо было записать ответ в виде целого числа или конечной десятичной дроби, и 2 задания с развернутым ответом.
Задания 1 – 10 с кратким ответом группировались исходя из тематической принадлежности заданий: алгебра, геометрия, реальная математика.
Задания 11 и 12 с развернутым ответом проверяли освоение математики на повышенном уровне.
В экзаменационной работе ГВЭ – 9 контролировались элементы содержания из следующих разделов (тем) курса математики.
Математика. 5 – 6 классы.
Алгебра. 7 – 9 классы.
Геометрия. 7 – 9 классы.
Вероятность и статистика. 7 – 9 классы.
Распределение заданий по основным содержательным разделам (темам) курса математики
| Содержательные блоки по темам курса | Количество заданий |
| Математика, алгебра | 6 |
| Геометрия | 4 |
| Реальная математика | 2 |
| Итого | 12 |
В экзаменационной работе были представлены задания базового и повышенного уровней сложности. К заданиям базового уровня относились 10 заданий с кратким ответом. Эти задания были направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. К заданиям повышенного уровня относились 2 задания. Эти задания были направлены на проверку освоения математики на повышенном уровне.
Оценивание экзаменационной работы ГВЭ – 9 по математике, маркированной буквой «А»
Каждое из заданий 1 – 10 с кратким ответом считалось выполненным, если записанный ответ совпадал с верным ответом. Задания 11 и 12 оценивались 2 баллами, если обоснованно получен верный ответ. Максимальный балл за всю работу – 14. Использовалась следующая шкала перевода суммы первичных баллов в пятибалльную систему оценивания.
Шкала перерасчета первичного балла за выполнение экзаменационной работы в отметку по пятибалльной шкале (ГВЭ – 9 по математике маркированной буквой «А»)
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Общий балл | 0 – 3 | 4 – 6 | 7 – 9 | 10 - 14 |
Каждый вариант экзаменационной работы, маркированного буквой «К», содержал 10 заданий с кратким ответом, в которых было необходимо записать ответ в виде целого числа или конечной десятичной дроби.
Задания 1 – 10 группировались исходя из тематической принадлежности заданий: алгебра, геометрия, реальная математика.
В экзаменационной работе ГВЭ – 9 контролировались элементы содержания из следующих разделов (тем) курса математики.
Математика. 5 – 6 классы.
Алгебра. 7 – 9 классы.
Геометрия. 7 – 9 классы.
Вероятность и статистика. 7 – 9 классы.
Распределение заданий по основным содержательным разделам (темам) курса математики
| Содержательные блоки по темам курса | Количество заданий |
| Математика, алгебра | 5 |
| Геометрия | 3 |
| Реальная математика | 2 |
| Итого | 10 |
Оценивание экзаменационной работы ГВЭ – 9 по математике, маркированной буквой «К»
Каждое из заданий 1 – 10 с кратким ответом считалось выполненным, если записанный ответ совпадал с верным ответом. Использовалась следующая шкала перевода суммы первичных баллов в пятибалльную систему оценивания.
Шкала перерасчета первичного балла за выполнение экзаменационной работы в отметку по пятибалльной шкале (ГВЭ – 9 по математике с маркировкой с буквой «К»)
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Общий балл | 0 – 2 | 3 – 5 | 6 – 8 | 9 - 10 |
Комплет экзаменационных материалов по математике для ГВЭ – 9 в устной форме состоял из 15 билетов, каждый из которых содержал 5 заданий, контролирующих элементы содержания курсов.
Математика. 5 – 6 классы.
Алгебра. 7 – 9 классы.
Геометрия. 7 – 9 классы.
Вероятность и статистика. 7 – 9 классы.
Распределение заданий по основным содержательным разделам (темам) курса математики
| Содержательные блоки по темам курса | Количество заданий |
| Математика, алгебра, вероятность и статистика | 3 |
| Геометрия | 2 |
| Итого | 5 |
Оценивание результата экзамена осуществлялось в соответствии со следующими критериями проверки каждого задания.
Критерии оценки выполнения каждого задания экзаменационной работы.
| Содержание критерия | Баллы |
| Ответ экзаменуемого характеризуется смысловой цельностью, речевой связностью и последовательностью изложения: Логические ошибки отсутствуют, последовательность изложения не нарушена;получен верный ответ ИЛИ допущена ошибка / неточность, которая после уточняющего вопроса экзаменатора исправлена экзаменуемым | 2 |
| Ответ экзаменуемого характеризуется смысловой цельностью, связностью и последовательностью изложения, но допущена одна ошибка / неточность, которую после уточняющего вопроса экзаменатора экзаменуемый не сумел исправить | 1 |
| Другие случаи, не соответствующие указанным выше критериям | 0 |
| Максимальный балл | 2 |
Максимальный первичный балл за экзаменационный билет – 10 баллов.
Шкала перевода первичного балла экзаменационной работы в отметку по пятибальной шкале.
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Общий балл | 0 - 4 | 5 - 6 | 7 - 8 | 9 - 10 |
На экзамене проверялся уровень сформированных представлений выпускников о математике как универсальном языке науки, об идеях и методах математики, овладение математическими знаниями и умениями, соответствующими Федеральному компоненту государственного стандарта общего образования, развитие логического мышления, пространственного воображения, алгоритмической культуры.
Результаты государственной итоговой аттестации признавались удовлетворительными, если выпускник при сдаче ГВЭ – 9 по математике получал отметку не ниже удовлетворительной.
Оценивание результата экзамена по математике осуществлялось следующим образом.
Если по результатам проверки экзаменационной работы суммы первичных баллов, выставленные двумя экспертами, совпадали, то эти баллы считались окончательными. Если по результатам проверки были получены суммы, расходящиеся на два или более первичных баллов, то по заданиям, в которых обнаружены расхождения, назначалась третья проверка; в других случаях расхождения оценки окончательной считалась более высокая оценка.
Характеристика участников ГВЭ - 9 по математике 2016 г.
Численность участников ГВЭ – 9 по математике в 2016 г. – 585 выпускников из образовательных организаций Алтайского края. В таблице 1 представлены результаты ГВЭ – 9 по МОУО (математика, 2016).
Таблица 1
Результаты ГВЭ – 9 по МОУО (математика, 2016)
| МОУО | Количество участников | Средняя отметка |
| Алейский район | 4 | 4,00 |
| Алтайский район | 1 | 4,00 |
| Бийский район | 3 | 4,00 |
| Волчихинский район | 3 | 4,00 |
| Егорьевский район | 10 | 3,10 |
| Завьяловский район | 4 | 3,75 |
| Залесовский район | 7 | 3,00 |
| Змеиногорский район | 1 | 4,00 |
| Заринский район | 1 | 4,00 |
| Зональный район | 1 | 5,00 |
| Калманский район | 5 | 4,20 |
| Каменский район | 25 | 3,40 |
| Ключевский район | 1 | 3,00 |
| Косихинский район | 5 | 3,60 |
| Краснощековский район | 1 | 3,00 |
| Крутихинский район | 2 | 5,00 |
| Кулундинский район | 17 | 3,35 |
| Курьинский район | 1 | 3,00 |
| Кытмановский район | 8 | 3,37 |
| Локтевский район | 15 | 3,33 |
| Мамонтовский район | 7 | 3,14 |
| Михайловский район | 2 | 4,50 |
| Павловский район | 5 | 3,00 |
| Первомайский район | 6 | 4,00 |
| Поспелихинский район | 10 | 3,70 |
| Ребрихинский район | 4 | 3,00 |
| Родинский район | 1 | 4,00 |
| Романовский район | 6 | 2,83 |
| Смоленский район | 4 | 3,50 |
| Советский район | 2 | 4,50 |
| Солонешенский район | 3 | 4,66 |
| Табунский район | 5 | 4,00 |
| Тальменский район | 20 | 3,45 |
| Топчихинский район | 16 | 3,37 |
| Третьяковский район | 2 | 4,50 |
| Троицкий район | 7 | 4,00 |
| Усть-Калманский район | 1 | 4,00 |
| Чарышский район | 3 | 3,00 |
| Шипуновский район | 12 | 3,33 |
| Шелаболихинский район | 10 | 3,10 |
| г. Алейск | 5 | 3,80 |
| г. Барнаул | 103 | 3,40 |
| г. Белокуриха | 2 | 4,00 |
| г. Бийск | 56 | 3,39 |
| г. Заринск | 3 | 5,00 |
| г. Новоалтайск | 7 | 4,14 |
| г. Рубцовск | 11 | 3,36 |
| г. Славгород | 3 | 3,00 |
| г. Яровое | 2 | 3,50 |
| Вечерняя школа № 1 | 33 | 3,48 |
| Вечерняя школа № 2 | 48 | 3,33 |
| Каменская спец школа | 2 | 5,00 |
| Краевые общеобразовательные учреждения | 26 | 3,88 |
| Краевые коррекционные образовательные учреждения | 43 | 3,93 |
| Итого: | 585 | 3,52 |
Общие сведения о среднем, минимальном и максимальном баллах ГВЭ по математике как по муниципальным органам управления образованием (МОУО), так и по Алтайскому краю приведены в таблице 2 и на рисунке.
Таблица 2




Из таблицы можно увидеть, что в 41 из 58-ти районов (городах) отмечается стопроцентное качество (4 ученика, получили неудовлетворительную отметку: 1 из Павловского района; 2 из г. Рубцовска; 1 из Романовского района). Максимальная средняя отметка 5 наблюдается только в 4 – х районах (городах): в Зональном районе, г. Заринске, Крутихинском районе и Каменской специальной школе. В прошлом году Крутихинский район также имел максимальную среднюю отметку. Средняя отметка по краю в 2016 г. – 3,52. В 25 районах средняя отметка выше краевой средней отметки. При этом наиболее низкая средняя отметка (2,83) в Романовском районе.
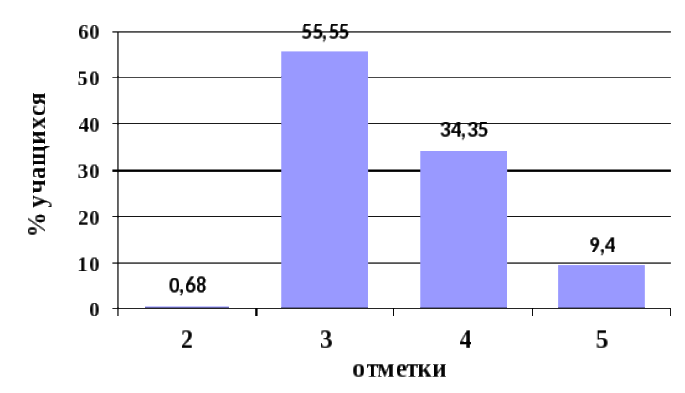
Рис. 1 Распределение участников ГВЭ по математике (%) в Алтайском крае по полученным отметкам в 2016 г.
Диаграмма на рисунке 1 отображает более оптимистичную картину по сравнению с результатами ОГЭ по математике в 2016 г., при этом можно заметить, что более половины учащихся сдали ГВЭ на «3», т.е. выпускники освоили программу на базовом уровне.
Рассмотрим типичные ошибки, допущенные девятиклассниками на государственном выпускном экзамене за 9 класс.
Вариант – 9 А; письменная форма; задание 1
Найти значение выражения:
Ответ: 1,7.
Решая задание, ученики допускали ошибки при переводе обыкновенной дроби в десятичную дробь, при сложении обыкновенных дробей с разными знаменателями складывали числители и знаменатели дробей. Причина таких ошибок – низкий уровень вычислительных навыков.
Вариант – 10 А; письменная форма; задание 2
Найти корень уравнения: 3х + 2 = 4х.
Ответ: 2.
При выполнении задания учащиеся не меняли знак при переносе слагаемого из одной части уравнения в другую. Причина такой ошибки – не сформированы действия самоконтроля. При выполнении проверки данная ошибка была бы исправлена.
Билет 8; устная форма; задание 2
Найти значение выражения: при х = - 1, у = 8.
Ответ: 15.
При выполнении задания учащиеся допускали вычислительные ошибки, подставляя значения переменных, предварительно не упростив выражение; упрощая выражение, затруднялись сократить дробь. Причина – низкий уровень вычислительных навыков, не сформированы умения разложения многочлена на множители и умение сокращения дроби.
Вариант 4К; письменная форма; задание 4
Установить соответствие между функциями и их графиками. (Вариант 4К письменная форма)

Ответ: А – 1, Б – 3, В – 2.
Причина ошибок учащихся в этом задании – незнание расположения графика линейной функции y = aх + b (a ≠ 0) в зависимости от коэффициентов.
Билет 8; устная форма; задание 2 в)
Указать решение неравенства
(-
[6; +
(-] U [6; +
[- 6; 6]
Допущена ошибка в алгоритме решения квадратного неравенства и вычислительная ошибка при вычислении корней квадратного трехчлена. Причина – у учащихся нет твердого владения базовым алгоритмом решения квадратного неравенства и низкий уровень вычислительных навыков.
Вариант 9 А; письменная форма; задание 6
Найдите площадь ромба, если его диагонали равны 34 и 4.
При решении этой задачи была допущена ошибка на знание формулы площади ромба S = Ученики перемножали длины диагоналей ромба, забыв поделить на 2. Причина не сформированы действия самоконтроля, решив задачу другим способом можно было бы исправить ошибку.
(Билет 11 устная форма)
Билет 11; устная форма; задание 2 а)
Решить уравнение: Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Ответ:
При нахождении дискриминанта учащиеся допускали ошибки в умножении и вычитании целых чисел, при возведении в квадрат отрицательного числа, в применении формул (даже при наличии справочных материалов).
Причина таких ошибок – не сформированы действия самоконтроля у обучающихся. Отсутствие действий самоконтроля не стимулировало учащихся к выполнению проверки, в ходе которой многие ошибки были бы ликвидированы.
Билет 11; устная форма; задание 1б)
На координатной прямой точки А, В, С и Д соответствуют числам
- 0,502; 0,25; 0,205; 0,52.





А В С Д
Какой точке соответствует число 0,25?
А 2) В 3) С 4) Д
Ответ: точка С.
Причиной массовых ошибок, различных неверных вариантов ответов в этом задании является недостаточный уровень умений сравнивать десятичные дроби, а также низкий уровень вычислительных умений.
Билет 8; устная форма; задание 1(а)
Найдите значение выражения:
Ответ: 0,8.
При выполнении этого задания были допущены ошибки при умножении десятичных дробей, при делении натурального числа на десятичную дробь. Причина – не сформированы вычислительные навыки действий с десятичными дробями и отсутствие действий самоконтроля.
Вариант 9 (А); письменная форма; задание 10
У бабушки 10 чашек: 7 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Ответ: 0,3. Засчитывался также ответ:
При решении данной задачи была допущена ошибка на знание формулы вероятности события или умения пользоваться этой формулой. Многие учащиеся заменили вопрос задачи собственным вопросом. Ребята искали вероятность того, что чашка будет с красными цветами. Причина последней ошибки – не сформирован самоконтроль.
Вариант 9 А; письменная форма; задание 9
Спортивный магазин проводит акцию. Любая футболка стоит 400 рублей. При покупке двух футболок – скидка на вторую футболку - 40 %. Сколько рублей придется заплатить за покупку двух футболок в период действия акции.
Ответ: 640 рублей.
При решении этой задачи многие выпускники не могли найти 40 % от 400, некоторые школьники вопрос задачи заменяли своим вопросом. Причина – не сформировано понятие процента, и нет самоконтроля.
Вариант 9 А; письменная форма; задание 11
Дорога между пунктами А и В состоит из подъема и спуска, а её длина равна 22 км. Турист прошел путь из А в В за 8 часов, из которых спуск занял 3 часа. С какой скоростью шел турист на спуске, если его скорость на подъеме меньше его скорости на спуске на 2 км/ч?
Решение: Пусть скорость туриста на спуске v км/ч, тогда его скорость на подъеме v – 2 км/ч. Получаем уравнение: 5(v - 2) + 3v = 22, откуда v = 4.
Ответ: 4 км/ч.
При решении задачи неверно составили математическую модель задачи. Решая линейное уравнение, не меняли знак при переносе слагаемых из одной части уравнения в другую.
При решении подобной задачи на ГВЭ в устной форме ученик неверно составил математическую модель задачи. При ответе ученика, ассистент не смог сформулировать уточняющий вопрос. Причина – на экзамене ассистенты не из числа учителей математики, поэтому не могут справиться со своими функциями ассистента.
Проведенный анализ типичных ошибок при выполнении учащимися заданий, дает основание определить наиболее слабо сформированные математические умения школьников. В связи с этим, в ходе освоения учащимися базовыми понятиями курса математики, умениями применять математические знания и решать практико-ориентированные задачи, а также в ходе подготовки к ГВЭ, учителю следует обратить внимание на развитие и совершенствование умений:
выполнять действия с обыкновенными и десятичными дробями;
проводить тождественные преобразования рациональных выражений;
выражать из формулы одну величину через другие;
осуществлять практические расчеты по формулам, составлять несложные формулы, выражающие зависимости между величинами;
решать уравнения, неравенства и их системы;
работать с математическим текстом, представленным в разном виде;
решать вероятностные задачи.
Опыт подготовки к ГВЭ показал положительную роль в подготовке к экзамену так называемых «репетиционных экзаменов». Кроме того, учитель может организовывать как на уроках, так и во внеурочное время обучающие мини-экзамены, используя, например, сайты http://alexlarin.net/ (генератор тестов на сайте формирует разные варианты), http://sdamgia.ru/ (выполнение заданий вариантов происходит на сайте в режиме on-line).
Практика работы учителей показывает, что в системе подготовки к ГВЭ по математике полезно проведение, по меньшей мере, двух диагностических работ в год. Эта работа будет более результативной, если после выполнения диагностических работ учитель тщательно проанализирует результаты.
Важным фактором в подготовке учащихся к ГВЭ является осведомленность учащегося, а также его родителей (законных представителей) о процедуре экзамена, особенностях его проведения. Основная официальная информация располагается на сайтах:
http://www.fipi.ru – Федеральный институт педагогических измерений;
http://gia.edu.ru/ – официальный информационный портал государственной итоговой аттестации.
Как известно, содержание экзаменационных работ формируется из открытого банка заданий по математике, размещенного на ФИПИ. Учителю целесообразно для успешной подготовки использовать все возможности открытого банка заданий для подготовки учащихся к ГВЭ.
Методические рекомендации по подготовке учащихся к ГВЭ по математике
Государственная (итоговая) аттестация выпускников 9 классов представляет собой открытую и независимую процедуру оценивания учебных достижений обучающихся, освоивших образовательные программы основного общего образования.
Подготовка к ГВЭ не должна сводится к «натаскиванию» девятиклассников на выполнение определенного типа задач, содержащихся в демонстрационной версии экзамена. Положительный опыт учителей математики показывает, что для улучшения результатов ГВЭ в процессе изучения и повторения учебного материала (практически на каждом уроке математики) необходима специальная подготовка учащихся к экзамену.
Сформулируем основные задачи систематической работы учителя по подготовке школьников к ГВЭ:
Обеспечить качественное освоение учебного материала (речь идет об овладении учеником новыми способами математических действий, знаниями и умениями), создавать условия для повторения и систематизации знаний, умений и способов действий по основным разделам школьной программы;
Своевременно выявлять пробелы в изучении школьниками математического материала и организовывать работу по их устранению;
Осуществлять пропедевтику типичных ошибок учащихся, допускаемых на экзаменах;
Развивать действия самоконтроля и самооценки;
Формировать умения самостоятельной учебной деятельности.
Обнаруженные проблемы в математической подготовке девятиклассников являются основанием для планирования учителем работы, направленной на формирование математической компетентности школьников и обеспечивающей успешную сдачу ГВЭ по математике. С целью качественной подготовки выпускников основной школы к государственному выпускному экзамену учителю следует обратить внимание на:
повышение уровня вычислительной культуры учащихся за счет применения различных методических приемов (например, сочетание письменных и устных вычислений, использование рациональных приемов вычислений, осуществление прикидки и оценки результатов вычислений, выполнение самоконтроля вычислений);
развитие культуры выполнения тождественных преобразований, которая предполагает качественные, устойчивые навыки выполнения тождественных преобразований, достижение полной свободы в их проведении;
формирование умений решать уравнения и неравенства. Большое значение при этом имеет работа учителя и учащихся по предупреждению ошибок, приводящих к нарушению равносильности в процессе решения уравнений и неравенств;
формирование умений находить вероятности случайных событий;
Предлагаемые методические рекомендации, раскрывают некоторые пути повышения качества математического образования.
Неоспоримым фактом признается то, что качество математического образования связано с формированием математической культуры школьников. Как показано в методике обучения математике, одним из средств формирования математической культуры является систематическое использование устных упражнений.
Активная умственная деятельность учащихся при получении новых знаний, их закреплении и трансформации в новые области возможна через методическую систему устных упражнений. Методическая система проведения устных упражнений включает: цели устных упражнений; содержание упражнений; методы обучения, используемые на устной работе; средства представления устных упражнений; формы организации учебной деятельности учащихся.
Методическая система устных упражнений служит эффективным средством в развитии познавательной потребности и познавательной самостоятельности, в развитии и мотивации к учению, и устойчивого интереса к математике. Методическая система устных упражнений обеспечит повышение качества математического образования школьников, а, следовательно, и успешную подготовку к ГВЭ.
Немаловажное значение имеет психологическая подготовка к экзамену.
Особенности психологической подготовки 1. Важно, чтобы каждый ученик определил для себя планируемый результат обучения, на какую оценку он должен сдать экзамен. Это не значит, что «потолок» должен занижаться, или оставаться неизменным, но на него нужно ориентироваться как ученику, так и учителю. Учителю необходимо ставить опережающую цель: дать «на выходе» для ребёнка результат выше, чем планировалось.
2. Уровень сложности заданий в некоторых случаях следует объявлять заранее, а в некоторых – только после его выполнения. Такой подход при спланированном подборе заданий приводит к значительному сдвигу как в самооценке школьника, в его чувстве уверенности в себе, так и в его умении без ошибок выполнять задания.
3. Следует учить школьника «технике сдачи экзамена». Эта техника включает в себя следующие моменты:
На консультациях, пробных и репетиционных экзаменах необходимо постоянно обращать внимание учащихся на то, сколько времени необходимо тратить на то или иное задание. Отсутствие привычки «напрягаться» в математике несколько часов подряд – одна из причин низкого качеств выполнения работы. Интеллект, как и мышцы нужно постоянно тренировать - от этого он только сильнее становится. Поэтому нужно постоянно повышать нагрузки и скорость выполнения заданий.
Ученики обычно сами знают, какие задания для них являются наиболее сложными. Таких «слабых» мест следует избегать при выполнении экзаменационной работы. Сначала нужно выполнять задания, в которых школьник ориентируется хорошо. Задача учителя состоит в том, чтобы школьник самостоятельно сумел набрать максимально возможное для него количество баллов, поэтому изречение «лучше меньше, да лучше» здесь оказывается вполне справедливым.
Обучение прикидке границ результатов, анализу ответа на предмет соответствия действительности, минимальной подстановке как приёму проверки ответа.
Следует учить школьников простым для проверки результатов сразу, а не «если останется время». Необходимо после решения задания приучать учеников внимательно перечитывать условие и вопрос (что нужно было найти?). Поскольку в учебниках дополнительных действий с ответами (например, найти сумму корней, а не сами корни) практически не встречается, многие школьники не обращают на них внимания, записывая при верно решённом задании неправильный ответ. Необходимо учить технике выбора ответа методом «исключения» явно неверного ответа. Особое внимание следует уделять заданиям, в которых формулировка звучит как «Выберите из данных выражений те, которые можно (или нельзя) преобразовать к виду…..». Самое главное здесь обратить внимание на ключевые слова «можно» или «нельзя», иначе ответ может получиться совершенно противоположным.
Ученик, просматривая работу от начала до конца, отмечает для себя задания, которые кажутся ему простыми и понятными и выполняются сходу, без особых раздумий. Именно их школьник выполняет первыми. Затем можно еще раз просмотреть работу и попробовать выполнить задания, которые не «поддались» сразу. Если ученик не может и после этого выполнить какое-то задание, то после контроля времени (3-4 минуты), следует перейти к другому заданию. Так необходимо делать несколько раз «по спирали» и делать то, что «созрело» к данному моменту.
Применяя описанные выше методические рекомендации, можно добиться того, что учащиеся успешно подготовятся к государственному выпускному экзамену в 9 классе.
























