Сабактын темасы. Идеалдык газ.
Сабактагы өтүлүүчү материалдар жана тапшырмалар:
Идеалдык газ ;
Газдагы басым менен механикадагы басымдан айырмалагыла;
Менделеев-Клайперон теөдемесин пайдаланып формула чыгаргыла;
Сабактын критерийлери:
Идеалдык газдын физикалык маанисин аныктай алса ;
Газдагы басым менен механикадагы басымдан айырмасын билсе;
Менделеев-Клайперон теңдемесин пайдаланып формула чыгарга алса;
Өзүн-өзү контролдоо сезимине ээ болуп сын көз карашын өнүктүрүүгө, терең жана кеңири ой жүгүртүүгө тарбияланышса;
Сабакка активдүү катышса;
Кайталоо үчүн жана жаңы темага өбөлгө түзүүчү суроолор:
Молекулалык-кинетикалык теория деп кандай теорияны айтабыз?
Молекулалык-кинетикалык теориянын негизги жоболору кайсылар?
Атом, молекула жөнүндө эмне билесиңер?
Салыштырмалуу атомдук масса деп эмнени айтабыз?
Моль масса жөнүндө эмне билесиөер?
Заттын саны деп эмнени айтабыз?
Авогадро саны.
Жаңы тема:
Катуу жана суюк заттардан айырмаланып газ өз формасын да, көлөмүн да сактабайт. Ал кай жерде боштук, же жылчык болсо, ошол жакты көздөй кете берет.
Сейректелген газдарда молекулалардын ортосундагы аралык, молекулалардын өз өлчөмдөрүнө караганда көп эсе чоөдук кылат. Ошондуктан, молекулалардын өз ара аракеттешүү күчү жокко эсе жана молекулалардын кинетикалык энергиясы, алардын өз ара аракеттешүүсүн потенциалдык энергиясынан бир кыйла чоө болуп эсептелет.
Мындай учурда газдардын молекулаларын өтө кичинекей катуу шарчалар деп кароого болот. Ал молекулалардын (шарчалардын) ортосунда тартышуу күчү жокко эсе да, алардын бир-бири менен кагылышуу убактысын өтө кыска деп эсептөөгө болот.
Реалдык газдардагы молекулалардын өз ара аракеттешүү күчтөрү өтө татаал.
Ошондуктан жөнөкөй болсун үчүн, илимде реалдык газдын ордуна анын физикалык модели катарында идеалдык газ алынат.
 Молекулалардын арасындагы өзара аракеттешүү күчү жокко эсе болгон газ идеалдык газ деп аталат.
Молекулалардын арасындагы өзара аракеттешүү күчү жокко эсе болгон газ идеалдык газ деп аталат.
Физикалык моделде реалдык газ абалын изилдөөчү өтө зарыл кассиеттер гана эске алынат. Реалдык сейректелген газ чынында эле өзүн идеалдык газ сыяктуу алып жүрөт.
Басым, бул басым күчүнүн аянт бирдигине болшогон катышы экени белгилүү.
Эми басым күчү  , аянты
, аянты  болсо, анда басым
болсо, анда басым  . (8.1)
. (8.1)
Анын бирдиги Па,  , сым. мам. мм.
, сым. мам. мм.
Газдын басымы манометр менен ченелет. Газдагы басым эмне себептен пайда болот деген суроо туулат. Молекулалак-кинетикалык теориянын негизинде газдын атомдору менен молекулалары хаотикалык кыймылда болгон соө, алар өзара бири-бири менен урунушат, өзү туурган же жайланышкан идиштин капталдарына урунушат.
Айрым молекуланын, же атомдун урунушу күчү аз, бирок көп молекуланын урунушуусу сезилээрлик өлчөмдө болот да ошол себептен газда басым пайда болот.
Окумуштуулар тарабынан жүргүзүлгөн кыйла татаал жана жөнөкөй тажрыйбалардын натыйжасында молекулалык-кинетикалык теорияда газдын басымы төмөнкү формула менен аныкталаары VIII класстын материалынан белгилүү. Бирок анын далили төмөнкүчө:
Кырынын узундугу  ге барабар болгон кубик берилсин (100-сүрөт), анын ичинде
ге барабар болгон кубик берилсин (100-сүрөт), анын ичинде  молекула жайланышкан дейли. Эгер бир молекуланын массасы
молекула жайланышкан дейли. Эгер бир молекуланын массасы  болсо жана ал
болсо жана ал  ылдамдыгы менен кубдун алдыөкы бетинен урунуп кайра артка кетсе (урунууну серпилгич шаарлар сыяктуу карайлы), анда ал
ылдамдыгы менен кубдун алдыөкы бетинен урунуп кайра артка кетсе (урунууну серпилгич шаарлар сыяктуу карайлы), анда ал  кыймыл санына барабар болот. Анда молекуланын импульс күчү
кыймыл санына барабар болот. Анда молекуланын импульс күчү  болот да кубиктин бетине жасалган
болот да кубиктин бетине жасалган  импульс күчүнө брарабар болот. Демек
импульс күчүнө брарабар болот. Демек
 , мында
, мында  - кубиктин бетине жасалган орточо басым күчү. Ал эми
- кубиктин бетине жасалган орточо басым күчү. Ал эми  , болгондуктан
, болгондуктан  , мындан
, мындан  жана (8.1) формуласы боюнча
жана (8.1) формуласы боюнча  болгондуктан
болгондуктан  же
же  бирок кубикте
бирок кубикте  молекула болгондуктан:
молекула болгондуктан:  мында
мында  – көлөм бирдигиндеги молекуланын санын (
– көлөм бирдигиндеги молекуланын санын (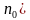 түшүндүрөт. Ошондой эле
түшүндүрөт. Ошондой эле  молекула оөго жана солго жылгандыктан анын
молекула оөго жана солго жылгандыктан анын  бөлүгү жылгандыгын билдирет. Демек , б.а.
бөлүгү жылгандыгын билдирет. Демек , б.а.
| (8.2) (8.2) формуласы идеалдык газдын кинетикалык теориясынын негизги теңдемеси деп аталат. Анын төмөнкүчө өзгөртүп түзсөк да болот: мында молекуланын алга жылуу кыймылынын орточо кинетикалык энергиясы деп аталат. Демек, (8.2) формуласы төмөнкүчө да жазылат:  , б.а. , б.а.   (8.3) (8.3)
|












Бирок ар түрдүү молекулалар түрдүү  ылдамдыкта кыймылдагандыктан, төмөнкү мааниге да ээ болот:
ылдамдыкта кыймылдагандыктан, төмөнкү мааниге да ээ болот:  Ошондуктан
Ошондуктан  тын ордуна анын
тын ордуна анын  орточо квадраттык маанисин алсак болот, б.а.
орточо квадраттык маанисин алсак болот, б.а.  (8.4) мында
(8.4) мында  – басым,
– басым,  – газдын бир молекуласынын массасы,
– газдын бир молекуласынын массасы,  – концентрация чоөдугу же көлөм бирдигиндеги молекуланын саны, ал эми
– концентрация чоөдугу же көлөм бирдигиндеги молекуланын саны, ал эми  – молекуланын алга жылуу кыймылынын орточо квадраттык ылдамдыгы. Демек, анын газда (8.4) формула боюнча
– молекуланын алга жылуу кыймылынын орточо квадраттык ылдамдыгы. Демек, анын газда (8.4) формула боюнча  ,
,  жана
жана  канча чоө болсо, газдагы басым ошончо чоө болот.
канча чоө болсо, газдагы басым ошончо чоө болот.
Мына ушул (8.2) жана (8.3) формулалары газдын молекулалык-кинетикикалык теориясынын негизги теөдемелери болуп эсептелет.
Газдын молекулалары тынымсыз хаотикалык кыймылда болгонун жана нормалдык шартта 1см3 көлөмдө 2,7  1019 молекула бар экендигин эске алсак, анда 1 секундада миллиондогон кагылышуулар болуп турат. Ошол кыймыл учурунда бир молекула экинчиси менен кагылышканга чейин кандайдыр бир аралыкты өтөт.Ошол молекуланын экинчиси менен кагылышканга чейинки кагылышпай өткөн аралык молекуланын эркин жол жүрүүсүнүн орточо аралыгы деп аталат. Орточо себеп ал өтө эле ар түрдүү аралыкта болот.Ошондуктан, анын орточо мааниси алынат да,
1019 молекула бар экендигин эске алсак, анда 1 секундада миллиондогон кагылышуулар болуп турат. Ошол кыймыл учурунда бир молекула экинчиси менен кагылышканга чейин кандайдыр бир аралыкты өтөт.Ошол молекуланын экинчиси менен кагылышканга чейинки кагылышпай өткөн аралык молекуланын эркин жол жүрүүсүнүн орточо аралыгы деп аталат. Орточо себеп ал өтө эле ар түрдүү аралыкта болот.Ошондуктан, анын орточо мааниси алынат да,  лямбда тамгасы менен белгиленет.
лямбда тамгасы менен белгиленет.
Газдын кыймыл ылдамдыктары да ар кандай. Ири молекулалар жайыраак, ал эми майдалары (кичинелери) чоөураак ылдамдык менен кыймылдашат. Ошондуктан орточо квадраттык ылдамдык түшүнүгү  пайда болгон.
пайда болгон.
Демек, ошого жараша ылдамдык менен шартталган молекуланын кинетикалык энергиясы да, сөзсүз, ар кандай чоөдукта болгондуктан орточо кинетикалык энергия деген түшүнүк пайда болгон да  үстүндөгү сызык орточо деген белгини түшүндүрөт. Ал эми
үстүндөгү сызык орточо деген белгини түшүндүрөт. Ал эми  молекуланын орточо квадраттык ылдамдыгын билдирет.
молекуланын орточо квадраттык ылдамдыгын билдирет.
Газдын молекулаларынын ылдамдыгы өтө эле ар түрдүү болгондуктан, газдын малекулаларынын ылдамдыгы дегенде алардын ылдамдыктарынын модулдарынын орточо арифметикалык мааниси дегенди түшүнүү керек.
Эгер айрым молекулалардын квадраттык ылдамдыктарын  деп белгилесек, молекулалардын саны N болсо, анын орточо арифметикалык мааниси:
деп белгилесек, молекулалардын саны N болсо, анын орточо арифметикалык мааниси:
болот. Анда ылдамдыктын  огундагы квадратынын орточосу:
огундагы квадратынын орточосу:  . (8.6)
. (8.6)
Бышыктоо, жыйынтыктоо:
Идеалдык газ деп кандай газды айтабыз?
Газдагы басым эмне себептен пайда болот?
Идеалдык газдын кинетикалык теориясынын негизги теңдемеси деп эмнени айтабыз?
Орточо кинетикалык энергиянын формуласы кандай экенин түшүндүргүлө.
Орточо квадраттык ылдамдыктын формуласы кандай түшүндүргүлө.
Үйгө берилүүчү тапшырмалар:
Орточо кинетикалык энергиянын формуласы кандай экенин түшүндүргүлө.
Орточо квадраттык ылдамдыктын формуласы кандай түшүндүргүлө.
Баалоо: Студенттер баалоо критерийлеринин негизинде бааланат







 Молекулалардын арасындагы өзара аракеттешүү күчү жокко эсе болгон газ идеалдык газ деп аталат.
Молекулалардын арасындагы өзара аракеттешүү күчү жокко эсе болгон газ идеалдык газ деп аталат. , аянты
, аянты  болсо, анда басым
болсо, анда басым  . (8.1)
. (8.1) , сым. мам. мм.
, сым. мам. мм. ге барабар болгон кубик берилсин (100-сүрөт), анын ичинде
ге барабар болгон кубик берилсин (100-сүрөт), анын ичинде  молекула жайланышкан дейли. Эгер бир молекуланын массасы
молекула жайланышкан дейли. Эгер бир молекуланын массасы  болсо жана ал
болсо жана ал  ылдамдыгы менен кубдун алдыөкы бетинен урунуп кайра артка кетсе (урунууну серпилгич шаарлар сыяктуу карайлы), анда ал
ылдамдыгы менен кубдун алдыөкы бетинен урунуп кайра артка кетсе (урунууну серпилгич шаарлар сыяктуу карайлы), анда ал  кыймыл санына барабар болот. Анда молекуланын импульс күчү
кыймыл санына барабар болот. Анда молекуланын импульс күчү  болот да кубиктин бетине жасалган
болот да кубиктин бетине жасалган  , мында
, мында  - кубиктин бетине жасалган орточо басым күчү. Ал эми
- кубиктин бетине жасалган орточо басым күчү. Ал эми  , болгондуктан
, болгондуктан  , мындан
, мындан  жана (8.1) формуласы боюнча
жана (8.1) формуласы боюнча  болгондуктан
болгондуктан  же
же  бирок кубикте
бирок кубикте  мында
мында  – көлөм бирдигиндеги молекуланын санын (
– көлөм бирдигиндеги молекуланын санын (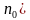 түшүндүрөт. Ошондой эле
түшүндүрөт. Ошондой эле 









