Метод крайнего
Особые, крайние объекты часто служат «краеугольным камнем» решения. Так, например, рассматривают наибольшее число, ближайшую точку, угловую точку, вырожденную окружность, предельный случай. Поэтому полезно сразу рассматривать особые, крайние объекты.
В задачах на метод крайнего работает метод минимального контрпримера: допустим, утверждение задачи неверно. Тогда существует минимальный в некотором смысле контрпример. И если окажется, что его можно ещё уменьшить, то получится искомое противоречие.
Пример 1. Плоскость разрезана вдоль N прямых общего положения, то есть таких, что никакие две не параллельны и никакие три не проходят через одну точку. Докажите, что к каждой прямой примыкает треугольник.
Решение. Выберем прямую и рассмотрим точки пересечения других прямых между собой. Среди этих точек пересечения выберем ближайшую к нашей прямой. Две прямые, проходящие через эту точку, пересекают исходную прямую и образуют с ней треугольник. Этот треугольник не могут пересекать другие прямые (подумайте, почему).
Пример 2. Докажите, что у любого многогранника есть две грани с одинаковым числом сторон.
Решение. Рассмотрим грань с наибольшим числом сторон. Обозначим эту грань G, число её сторон n. К каждой стороне G примыкает грань многогранника, всего примыкающих граней n. Число сторон у каждой грани заключено между 3 и n − 1, всего
n − 3 возможности. Поскольку число возможностей меньше числа примыкающих граней, то по принципу Дирихле одна из возможностей повторится. Таким образом, среди граней, примыкающих к грани G, найдутся две грани с одинаковым числом сторон.
Пример 3. В каждой клетке шахматной доски записано число. Оказалось, что любое число равно среднему арифметическому чисел, записанных в соседних (по стороне) клетках. Докажите, что все числа равны.
Решение. Рассмотрим наибольшее из чисел. Оно равно своим соседям. Поскольку любые два числа соединяются цепочкой соседних чисел, все числа равны.
Пример 4. Из точки внутри выпуклого многоугольника опускают перпендикуляры на его стороны или их продолжения. Докажите, что хотя бы один перпендикуляр попадёт на сторону.
Указание. Рассмотрите ближайшую точку границы.
Пример 5. Докажите, что число 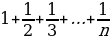 не является целым. Указание. Рассмотрите максимальную из степеней двойки, входящих в знаменатели слагаемых.
не является целым. Указание. Рассмотрите максимальную из степеней двойки, входящих в знаменатели слагаемых.
Задачи для самостоятельного решения
1. Путешественник отправился из своего родного города A в самый удалённый от него город страны B; затем из B – в самый удалённый от него город C и т. д. Докажите, что если C не совпадает с A, то путешественник никогда не вернется домой. (Расстояния между городами страны различны).
2. Назовём автобусный билет (c шестизначным номером) счастливым, если сумма цифр его номера делится на 7. Могут ли два билета подряд быть счастливыми?
3. В одну из голов стоглавого дракона пришла мысль расположить свои головы так, чтобы каждая находилась между двумя другими. Сможет ли он это сделать? (Головы дракона можно считать точками в пространстве.)
4. На столе лежат одинаковые монеты без наложений. Докажите, что найдётся монета, которая касается не более трёх других.
5. На столе лежат произвольные монеты без наложений. Докажите, что найдётся монета, которая касается не более пяти других.
6. На столе лежат монеты без наложений. Докажите, что одну из них можно передвинуть по столу к его краю, не сдвинув других монет.
7. На полях шахматной доски расставлены целые числа, причём никакое число не встречается дважды. Докажите, что есть пара соседних (имеющих общую сторону) клеток, числа в которых отличаются не меньше, чем на 5.
8. На окружности стоят 30 чисел, каждое из которых равно модулю разности двух следующих за ним по часовой стрелке. Сумма всех чисел равна 1. Найдите эти числа и порядок их следования по окружности.
9. На прямой расположена колония из конечного числа бактерий. В моменты 1, 2, 3, . . . некоторые из бактерий могут погибать; новых бактерий не возникает ни в один момент. Погибают те и только те бактерии, от которых ни слева на расстоянии 1, ни справа на расстоянии 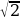 нет бактерий. Существует ли колония бактерий, которая будет жить вечно?
нет бактерий. Существует ли колония бактерий, которая будет жить вечно?
10. В течение дня в библиотеке побывало 100 читателей. Оказалось, что в тот день из любых трёх читателей двое в библиотеке встретились. Докажите, что сотрудник библиотеки мог сделать важное сообщение в такие два момента времени, чтобы все 100 человек его услышали. (Каждый читатель побывал в библиотеке только один раз.)
11. На плоскости отмечено несколько прямых. Известно, что через точку пересечения любых двух отмеченных прямых, проходит по крайней мере ещё одна. Докажите, что все отмеченные прямые проходят через одну точку.
12. На плоскости отметили несколько точек. Точки, находящиеся от данной на наименьшем расстоянии, назовём ближайшими (их может быть несколько). Докажите, что найдётся точка, имеющая не более трёх ближайших.
13. Найдите наибольшее значение выражения x1x2+x2x3+ : : :+x99x100, где x1, x2, . . . , x100 – неотрицательные числа, сумма которых равна 1.







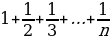 не является целым. Указание. Рассмотрите максимальную из степеней двойки, входящих в знаменатели слагаемых.
не является целым. Указание. Рассмотрите максимальную из степеней двойки, входящих в знаменатели слагаемых. 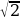 нет бактерий. Существует ли колония бактерий, которая будет жить вечно?
нет бактерий. Существует ли колония бактерий, которая будет жить вечно? 


















