Соответствие
Мы говорим, что между двумя множествами установлено взаимно однозначное соответствие, если каждому элементу первого множества поставлен в соответствие элемент второго множества, при этом каждый элемент второго множества соответствует ровно одному элементу первого множества. Иначе говоря, мы разбили элементы обоих множеств на пары, причём в каждую пару входит по элементу из каждого множества. Если между двумя конечными множествами установлено взаимно однозначное соответствие, то можно утверждать, что они содержат одинаковое количество элементов, даже если пересчитать элементы этих множеств мы не можем. К примеру, чтобы узнать, равное ли количество дам и кавалеров пришло на бал, достаточно объявить танец. Если никто не остался без пары, значит тех и других поровну. Если же мы установили соответствие между всеми элементами одного множества и частью элементов другого множества, то количество элементов в первом множестве меньше, чем во втором.
Пример 1. В выпуклом n-угольнике никакие три диагонали не пересекаются в одной точке. Сколько точек пересечения у этих диагоналей? (Концы диагоналей не считаются точками пересечения.)
Решение. Каждой точке пересечения диагоналей соответствует четвёрка вершин – концов соответствующих диагоналей. Имеется и обратное соответствие: каждой четвёрке вершин соответствует точка пересечения диагоналей образованного ими четырёхугольника. Поэтому число точек пересечения диагоналей равно количеству четвёрок вершин, т. е. числу сочетаний из n по 4.
Пример 2. Придворный астролог царя Гороха называет время суток хорошим, если на часах с центральной секундной стрелкой при мгновенном обходе циферблата по ходу часов минутная стрелка встречается после часовой и перед секундной. Какого времени в сутках больше: хорошего или плохого?
Решение. Основная идея: если стрелки показывают хорошее время, то их зеркальное отражение показывает плохое, и наоборот.
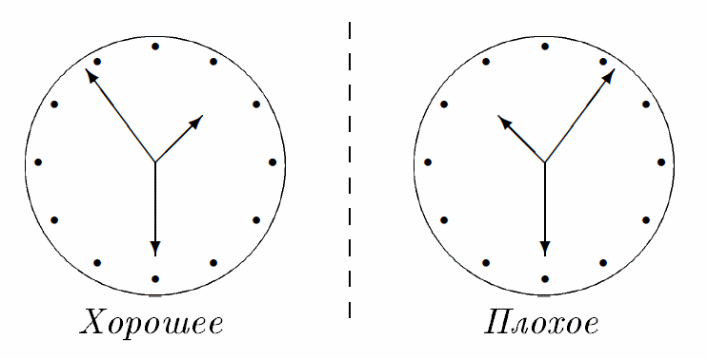
В полночь стрелки совпадают. Если пустить часы назад, то стрелки, будут показывать какое-то вчерашнее время, а их расположение будет зеркально симметричным расположению стрелок на обычных часах. Итак, каждому хорошему моменту сегодня соответствует плохой момент вчера. Причем интервалу хорошего времени соответствует интервал плохого. Значит, хорошего времени сегодня столько же, сколько было плохого вчера. Поэтому хорошего и плохого времени в сутках поровну.
Пример 3. Номер автобусного билета состоит из 6 цифр. Билет называют счастливым, если сумма первых трёх цифр его номера равна сумме трёх последних цифр. Каких автобусных билетов больше: счастливых или тех, чьи номера делятся на 11?
Решение. Счастливые билеты, упомянутые в условии, будем называть счастливыми по-московски. Назовём билет счастливым по-питерски, если сумма цифр его номера, стоящих на чётных местах, равна сумме цифр, стоящих на нечётных местах. Выясним сначала, каких счастливых билетов больше – по-московски или по-питерски? Их поровну, поскольку между ними можно установить взаимно однозначное соответствие следующим образом. Переставим цифры номера билета, счастливого по-московски: первые три цифры поставим на нечётные места (первое, третье и пятое), а последние три цифры – на чётные (например, номер 129345 превратится в 132495.) Получим счастливый по-питерски билет. Теперь заметим, что номер любого билета, счастливого по-питерски делится на 11. (Признак делимости на 11: «Число делится на 11, тогда и только тогда, когда сумма его цифр, стоящих на чётных местах, минус сумма цифр, стоящих на нечётных местах, делится на 11».) Обратное неверно: существуют не счастливые по-питерски билеты, номера которых делятся на 11, например, если разность сумм цифр, стоящих на нечётных и чётных местах, равна 11. Поэтому билетов с номерами, делящимися на 11 больше, чем счастливых по-питерски, а значит и по-московски.
Соответствие помогает не только определять, какое множество больше, но и решать другие задачи. Приведём несколько примеров.
Пример 4. Найдите сумму чисел 1 + 2 + 3 + … + 100.
Решение (его, согласно легенде, придумал маленький Гаусс). Напишем ту же сумму в обратном порядке и сложим числа по столбцам:
x = 1 + 2 + 3 + . . . + 100
x = 100 + 99 + 98 + . . . + 1
2x = 101 + 101 + 101 + . . . + 101 = 10100. Откуда х = 10100 : 2 = 5050
Ответ: 5050.
Объект может стать более естественным, если у него найдётся пара. Например, вместе с иррациональностью 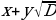 рассматривают сопряжённую иррациональность
рассматривают сопряжённую иррациональность 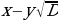 .
.
Пример 5. Докажите, что в числе (6 + 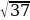 )999 первые 999 цифр справа после запятой | нули.
)999 первые 999 цифр справа после запятой | нули.
Идея решения. Добавим сопряжённую иррациональность (6 − 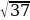 )999 и заметим, что сумма (6+
)999 и заметим, что сумма (6+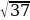 )999+(6 −
)999+(6 − 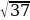 )999 есть число целое, а член (6 −
)999 есть число целое, а член (6 − 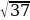 )999 достаточно мал.
)999 достаточно мал.
Задачи для самостоятельного решения
1. Докажите, что дроби 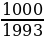 и
и 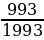 имеют одинаковую длину периодов.
имеют одинаковую длину периодов.
2. Докажите, что сумма номеров счастливых билетов делится на 13. (Определение см. в примере 3.)
3. По кругу расставлены 8 точек. Двое по очереди соединяют их отрезками. Первый отрезок проводится произвольно, а каждый следующий отрезок начинается из конца предыдущего. Проигрывает тот, кто не может провести новый отрезок (дважды проводить отрезок нельзя). Предположим, что игроки не делают ошибок. Kто из них победит: первый или второй?
4. На окружности даны 1987 точек, одна из них отмечена. Рассмотрим всевозможные выпуклые многоугольники с вершинами в этих точках. Каких многоугольников больше: тех, которые содержат отмеченную точку, или тех, которые её не содержат?
5. Докажите, что число (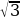 −
− 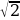 )999 представимо в виде a
)999 представимо в виде a 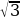 − b
− b 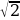 , причём
, причём
3a2 − 2b2 = 1.
6. Существуют ли такие рациональные 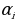 и
и 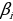 , что
, что
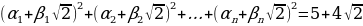 ?
?
7. Докажите, что число (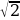 − 1)n представимо в виде
− 1)n представимо в виде 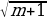 −
− 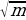 , где m ∈ N.
, где m ∈ N.
8. Двое бросают монетку: один бросил её 10 раз, другой − 11. Чему равна вероятность того, что у второго монета упала орлом большее число раз, чем у первого?
9. В самолёте 100 мест, на авиарейс проданы 100 билетов, пронумерованных соответственно местам. В салон пассажиры входят по очереди. Первой входит сумасшедшая старушка, которая, не глядя на билет занимает первое попавшееся место. Каждый следующий пассажир, входя в салон ищет своё место, и если оно свободно, то занимает его. Если же его место занято, то садится на произвольное место. Какова вероятность того, что последний вошедший пассажир сядет на своё место?








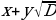 рассматривают сопряжённую иррациональность
рассматривают сопряжённую иррациональность 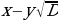 .
. 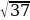 )999 первые 999 цифр справа после запятой | нули.
)999 первые 999 цифр справа после запятой | нули. 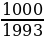 и
и 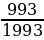 имеют одинаковую длину периодов.
имеют одинаковую длину периодов. 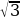 −
− 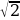 )999 представимо в виде a
)999 представимо в виде a 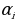 и
и 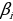 , что
, что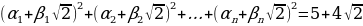 ?
?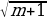 −
− 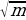 , где m ∈ N.
, где m ∈ N. 









