Министерство образования, науки и молодежной политики Нижегородской области
Государственное бюджетное профессиональное образовательное учреждение
«Шахунский колледж аграрной индустрии»
(ГБПОУ ШКАИ)
Индивидуальный проект
По дисциплине: математика
Тема: «Методы решения квадратных уравнений с использованием компьютерных программ»
Автор: обучающийся 1 курса, группы 170
Специальность 09.02.07 Информационные системы и программирование
Мазур Данил Алексеевич
Руководитель: преподаватель
математики Соколова Ирина Викторовна
Оценка:___________/____________/
подпись руководителя
г. Шахунья
2020 г.
Содержание
Введение 3
Глава 1. Теоретические основы методов решения квадратных уравнений 5
1.1. История развития квадратных уравнений в Древнем Вавилоне, Индии и в Европе XIII – XVII вв 5
1.2. Как составлял и решал Диофант и ал – Хорезми квадратные уравнения и о теореме Виета 9
Глава 2. Исследовательская часть методов решения квадратных уравнений 12
2.1. Способы решения квадратных уравнений 12
2.2. Как реализуется метод решения квадратных уравнений на компьютере 23
Заключение 35
Список литературы 37
Приложения 38
Введение
Актуальность темы исследования, заключается в том, что практически все, что окружает современного человека - это все так или иначе связано с математикой. А достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем решение многих практических задач сводится к решению квадратных уравнений.
Квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры. Они представляют собой большой и важный класс уравнений, которые решаются как с помощью формул, так и с помощью нестандартных способов. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных уравнений и неравенств.
Проблема состоит в том, что учащиеся не знаю более легкие способы решения квадратных уравнений,
Объект исследования: квадратные уравнения.
Предмет исследования: методы решения квадратных уравнений.
В курсе математики мы изучили квадратные уравнения, узнали различные способы решения уравнений второй степени. Этот материал нас заинтересовал, и мы решили узнать, существуют ли другие способы решения квадратных уравнений. Это определило тему нашего исследования: «Квадратные уравнения и методы их решения».
В учебниках мы знакомимся с несколькими видами квадратных уравнений, и отрабатываем решение по формулам. Нам пришла идея рассмотреть те способы решения квадратных уравнений, на которые недостаточно времени уделено на уроках или совсем не рассматриваются. Вместе с тем, современные научно–методические исследования показывают, что использование разнообразных методов и способов позволяет значительно повысить эффективность и качество изучения решений квадратных уравнений.
Цель исследования изучение различных методов решения квадратных уравнений.
На основании поставленной цели мы ставим перед собой следующие задачи:
Произвести анализ учебно-методической литературы по решению квадратных уравнений.
Произвести анализ различных способов решения квадратных уравнений.
Изучить различные способы решения квадратных уравнений, апробировать их на практике, собрать дидактический материал. (Приложения А-В).
Гипотеза существуют методы решения квадратных уравнений не изучаемые в колледже.
Применяемые методы исследования:
эмпирическую базу исследования составляют научные статьи и литература, нормативно-правовые акты, статические данные, отчеты, результаты социологического исследования.
теоретические: сравнение, классификация, анализ, обобщение.
Новизна исследования состоит в комплексном рассмотрении способов решения уравнений второй степени.
Практическая значимость работы состоит в приобретении навыка решения квадратных уравнений различными способами.
Структура работы состоит из введения, теоретической и практической частей, заключения, списка литературы и приложения.
Глава 1. Теоретическая часть методов решения квадратных уравнений
1.1. История развития квадратных уравнений в Древнем Вавилоне, Индии и в Европе XIII – XVII вв
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Уравнения - это наиболее объёмная тема всего курса математики.
В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. «Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37.», - поучал во II тысячелетии до новой эры египетский писец Ахмес.
В древних математических задачах Междуречья, Индии [2, c. 23], Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.
Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты правильно нашел». В этом смысле исключением является «Арифметика» греческого математика Диофанта Александрийского (III в.) - собрание задач на составление уравнений с систематическим изложением их решений.
Уравнения второй степени умели решать еще в древнем Вавилоне. Математики Древней Греции решали квадратные уравнения с помощью геометрических построений [2, c. 21]; например, Евклид - при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактах.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
В Древнем Вавилоне
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения: X2 + X = ѕ; X2 - X = 14,5 [2, c. 20].
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
В Индии
Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам» [4, c. 23], составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ах2 + bх = с, а 0. (1)
В уравнении (1) коэффициенты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму. Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Задача 13.
«Обезьянок резвых стая А двенадцать по лианам…
Власть поевши, развлекалась. Стали прыгать, повисая…
Их в квадрате часть восьмая Сколько ж было обезьянок,
На поляне забавлялась. Ты скажи мне, в этой стае?»
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений (рис. 1).

Рисунок 1 - Часть страницы из алгебры Бхаскары «Видиса Ганита»
Соответствующее задаче 13 уравнение: (x/8)2 + 12 = x.
Бхаскара пишет под видом: х2 - 64х = -768 и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 322, получая затем:
х2 - 64х + 322 = -768 + 1024,
(х - 32)2 = 256, х - 32 = ± 16, х1 = 16, х2 = 48.
В Европе XIII - XVII вв.
Формулы решения квадратных уравнений по образцу ал - Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Этот объемистый труд, в котором отражено влияние математики, как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники XVI - XVII вв. и частично XVIII.
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду: х2 + bx = с, при всевозможных комбинациях знаков коэффициентов b, с было сформулировано в Европе лишь в 1544 г. М. Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря труда Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
1.2. Как составлял и решал Диофант и ал – Хорезми квадратные уравнения и о теореме Виета
Как составлял и решал Диофант квадратные уравнения
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней. При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные. Вот, к примеру, одна из его задач.
Задача 11. «Найти два числа, зная, что их сумма равна 20, а произведение - 96»
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100.
Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х, другое же меньше, т.е. 10 - х. Разность между ними 2х. Отсюда уравнение:
(10 + х)(10 - х) = 96 или же: 100 - х2 = 96,
х2 - 4 = 0
Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа. Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения:
у(20 - у) = 96,
у2 - 20у + 96 = 0
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).
О теореме Виета
Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. следующим образом: «Если B + D, умноженное на A - A2, равно BD, то A равно В и равно D».
Чтобы понять Виета, следует вспомнить, что А, как и всякая гласная буква, означало у него неизвестное (наше х), гласные же В,D - коэффициенты при неизвестном. На языке современной алгебры вышеприведенная формулировка Виета означает: если имеет место
(а + b)х - х2 = ab, т.е. х2 - (а + b)х + аb = 0, то х1 = а, х2 = b.
Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виет установил единообразие в приемах решения уравнений [2, c. 25].
Однако символика Виета еще далека от современного вида. Он не признавал отрицательных чисел и поэтому при решении уравнений рассматривал лишь случаи, когда все корни положительны.
У ал – Хорезми
В алгебраическом трактате ал - Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корнями», т.е. ах2 + с = bх.
2) «Квадраты равны числу», т.е. ах2 = с.
3) «Корни равны числу», т.е. ах = с.
4) «Квадраты и числа равны корням», т.е. ах2 + с = bх.
5) «Квадраты и корни равны числу», т.е. ах2+ bx = с.
6) «Корни и числа равны квадратам», т.е. bx + с = ах2.
Для ал - Хорезми, избегавшего употребления отрицательных чисел, члены каждого их этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал - джабр и ал - мукабала. Его решения, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал - Хорезми, как и все математики до XVII в., е учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал - Хорезми на частных числовых примерах излагает правила решения, а затем и геометрические доказательства.
Задача 14. «Квадрат и число 21 равны 10 корням. Найти корень» (подразумевается корень уравнения х2 + 21 = 10х).
Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножишь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат ал - Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
Глава 2. Исследовательская часть методов решения квадратных уравнений
2.1. Способы решения квадратных уравнений
Квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (7 класс), до окончания вуза.
В курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения (Приложение А).
Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно остановимся на каждом из них.
1 способ: Разложение левой части уравнения на множители
Решим уравнение
х2 + 10х - 24 = 0.
Разложим левую часть на множители:
х2 + 10х - 24 = х2 + 12х - 2х - 24 = х(х + 12) - 2(х + 12) = (х + 12)(х - 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х - 2) = 0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = - 12. Это означает, что число 2 и - 12 являются корнями уравнения х2 + 10х - 24 = 0.
2 способ: Метод выделения полного квадрата
Решим уравнение х2 + 6х - 7 = 0.
Выделим в левой части полный квадрат.
Для этого запишем выражение х2 + 6х в следующем виде:
х2 + 6х = х2 + 2 • х • 3.
В полученном выражении первое слагаемое - квадрат числа х, а второе - удвоенное произведение х на 3. Поэтому чтобы получить полный квадрат, нужно прибавить 32, так как х2 + 2 • х • 3 + 32 = (х + 3)2.
Преобразуем теперь левую часть уравнения
х2 + 6х - 7 = 0, прибавляя к ней и вычитая 32. Имеем:
х2 + 6х - 7 = х2 + 2 • х • 3 + 32 - 32 - 7 = (х + 3)2 - 9 - 7 = (х + 3)2 - 16.
Таким образом, данное уравнение можно записать так:
(х + 3)2 - 16 =0, (х + 3)2 = 16.
Следовательно, х + 3 - 4 = 0, х1 = 1, или х + 3 = -4, х2 = -7.
3 способ: Решение квадратных уравнений по формуле
Умножим обе части уравнения
ах2+ bх + с = 0, а ≠ 0
на 4а и последовательно имеем:
4а2х2 + 4аbх + 4ас = 0,
((2ах)2 + 2ах • b + b2) - b2 + 4ac = 0,
(2ax + b)2 = b2 - 4ac,
2ax + b = ± √ b2 - 4ac,
2ax = - b ± √ b2 - 4ac,
 (2)
(2)
Примеры. Сколько корней имеет уравнение?
а) 4х2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b2 - 4ac = 72 - 4 • 4 • 3 = 49 - 48 = 1,
D 0, два разных корня;
Таким образом, в случае положительного дискриминанта, т.е. при
b2 - 4ac 0, уравнение ах2 + bх + с = 0 имеет два различных корня.
б)4х2 - 4х + 1 = 0,
а = 4, b = - 4, с = 1, D = b2 - 4ac = (-4)2 - 4 • 4 • 1= 16 - 16 = 0,
D = 0, один корень;
Итак, если дискриминант равен нулю, т.е. b2 - 4ac = 0, то уравнение
ах2+ bх + с = 0 имеет единственный корень,
в)2х2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b2 - 4ac = 32 - 4 • 2 • 4 = 9 - 32 = - 13 , D
Данное уравнение корней не имеет.
Итак, если дискриминант отрицателен, т.е. b2 - 4ac
ах2+ bх + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах2+ bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
4 способ: Решение уравнений с использованием теоремы Виета
Как известно, приведенное квадратное уравнение имеет вид
х2 + px + c = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x 1x2 = q,
1x2 = q,
x1 + x2 = - p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р 0, то оба корня отрицательны, если р
Например, x2 – 3x + 2 = 0; x1 = 2 и x2 = 1, так как q = 2 0 и p = - 3
x2 + 8x + 7 = 0; x1 = - 7 и x2 = - 1, так как q = 7 0 и p= 8 0.
б) Если свободный член q приведенного уравнения (1) отрицателен (q 0 .
Пример: x2 + 4x – 5 = 0; x1 = - 5 и x2 = 1, так как q= - 5 0;
x2 – 8x – 9 = 0; x1 = 9 и x2 = - 1, так как q = - 9
5 способ: Решение уравнений способом «переброски»(Приложение В).
Рассмотрим квадратное уравнение ах2+ bх + с = 0, где а ≠ 0.
Умножая обе его части на а, получаем уравнение
а2х2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению
у2 + by + ас = 0,равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = у1/а и х1 = у2/а.
При этом способе коэффициента умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Пример. Решим уравнение 2х2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у2 – 11у + 30 = 0.
Согласно теореме Виета
у



 1= 5 х1 = 5/2 x1 = 2,5
1= 5 х1 = 5/2 x1 = 2,5
у2 = 6 x2 = 6/2 x2 = 3.
Ответ: 2,5; 3.
6 способ: Свойства коэффициентов квадратного уравнения (Приложение В)
А. Пусть дано квадратное уравнение
ах2+ bх + с = 0, где а ≠ 0.
1) Если, а + b + с = 0 (т.е. сумма коэффициентов равна нулю), то
х1= 1
х2 = с/а.
Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение
x2 + b/a • x + c/a = 0.
 Согласно теореме Виета
Согласно теореме Виета
x1 + x2 = - b/a,
x1x2 = 1 • c/a.
По условию а – b + с = 0, откуда b = а + с. Таким образом,
x 1 + x2 = - а + b/a= -1 – c/a,
1 + x2 = - а + b/a= -1 – c/a,
x1x2 = - 1 • ( - c/a),
т.е. х1 = -1 и х2 = c/a, что м требовалось доказать.
Примеры.
Решим уравнение 345х2 – 137х – 208 = 0.
Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то
х1 = 1, х2 = c/a = -208/345.
Ответ: 1; -208/345.
Решим уравнение 132х2 – 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то
х1 = 1, х2 = c/a = 115/132.
Ответ: 1; 115/132.
Б. Если второй коэффициент b = 2k– четное число, то формулу корней
 (3)
(3)
Пример.
Решим уравнение 3х2 — 14х + 16 = 0.
Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;
D = k2 – ac = (- 7)2 – 3 • 16 = 49 – 48 = 1, D 0, два различных корня;

Ответ: 2; 8/3
В. Приведенное уравнениех2 + рх + q= 0совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней принимает вид:
 (4)
(4) (5)
(5)
Формулу (3) особенно удобно использовать, когда р - четное число.

Пример. Решим уравнение х2 – 14х – 15 = 0.
Решение. Имеем: х1, 2 =7 ± 8,
Ответ: х1 = 15; х2 = -1.
7 способ: Решение квадратных уравнений с помощью циркуля и линейки

Рисунок 2 - Нахождение корня квадратного уравнения с помощью циркуля и линейки
Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика. Найти корни квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис. 2) [4, c. 34].
Допустим, что искомая окружность пересекает ось абсцисс в точках В(х1; 0) и D (х2; 0), где х1 и х2 - корни уравнения ах2 + bх + с = 0, и проходит через точки А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a.
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому
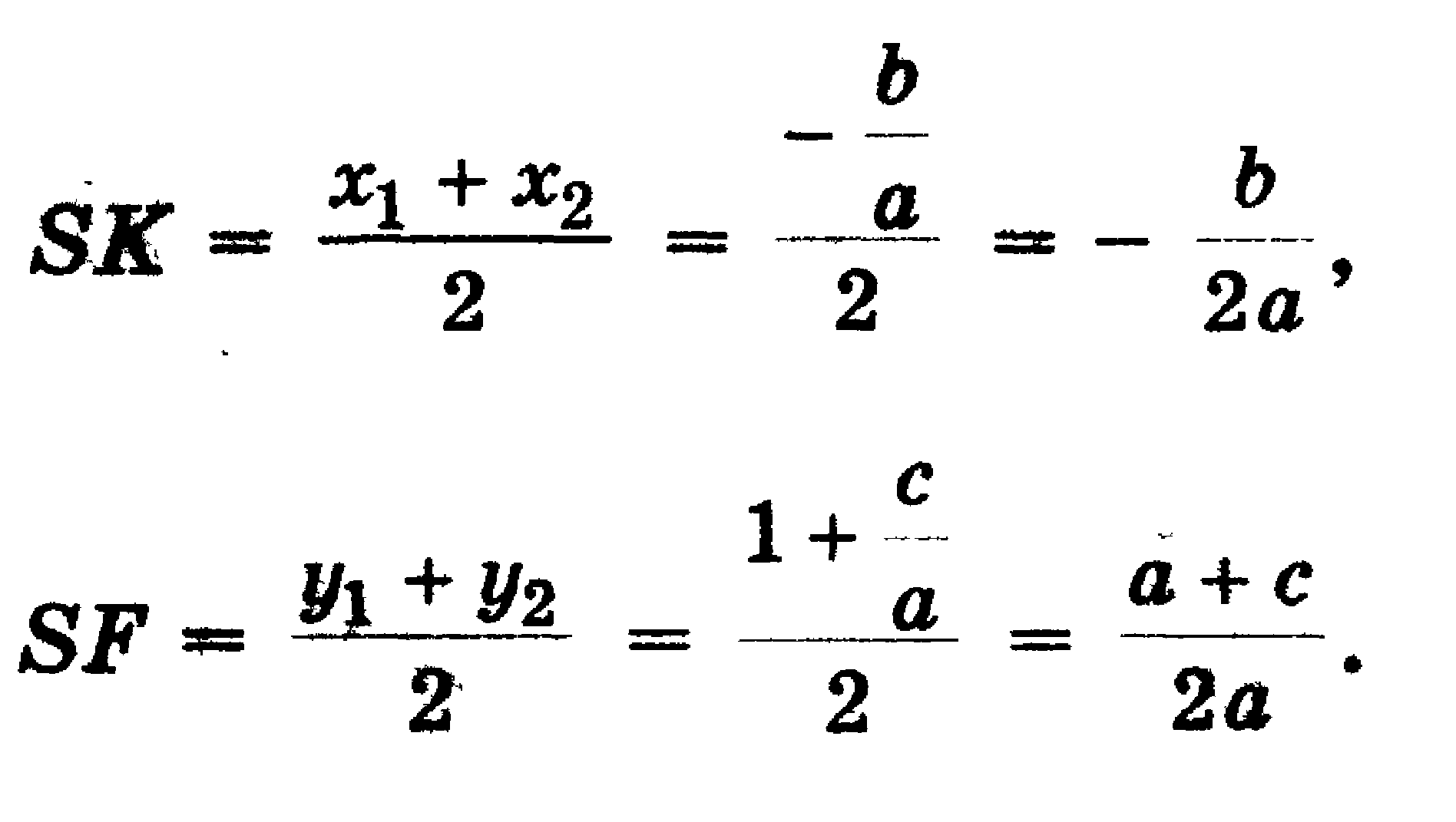
 (6)
(6)
Итак:
1) построим точки (центр окружности) и A(0; 1);
2) проведем окружность с радиусом SA;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра (AS SK, или R a + c/2a), окружность пересекает ось Ох в двух точках (рис. 3, а) В(х1; 0) и D(х2; 0), где х1 и х2 - корни квадратного уравнения ах2 + bх + с = 0.
 (7)
(7)
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 3, б) в точке В(х1; 0), где х1 - корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис. 3, в), в этом случае уравнение не имеет решения.



Рисунок 3 - Три случая нахождения центра окружности в точке пересечения перпендикуляторов
 (8)
(8)
 (9)
(9)
 (10)
(10)
Пример. Решим уравнение х2 - 2х - 3 = 0 (рис. 4).
Решение. Определим координаты точки центра окружности по формулам:
Проведем окружность радиуса SA, где А (0; 1).
Рисунок 4 - Окружность радиуса SA уравнения х2 - 2х - 3 = 0
Ответ: х1 = - 1; х2 = 3.
8 способ: Решение квадратных уравнений с помощью номограммы
Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с. 93 (В.М. Брадис, Четырехзначные математические таблицы для средней школы. 23-е. изд./ В.М. Брадис, / - М.: Просвещение, 2020. С. 93.) [1, c. 83].
Таблица XXII. Номограмма для решения уравнения z2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициент там определить корни уравнения.
Рисунок 5 - Криволинейная шкала номограммы
Криволинейная шкала номограммы построена по формулам (рис. 5):
(11)
Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию
(12)
откуда после подстановок и упрощений вытекает уравнение
z2 + pz + q = 0,
причем буква z означает метку любой точки криволинейной шкалы.
Примеры.
1) Для уравнения z2 - 9z + 8 = 0 номограмма дает корни z1 = 8,0 и z2 = 1,0 (рис. 6).
Рисунок 6 - Номограмма дающая корни
2) Решим с помощью номограммы уравнение
2z2 - 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение
z2 - 4,5z + 1 = 0.
Номограмма дает корни z1 = 4 и z2 = 0,5.
3) Для уравнения
z2 - 25z + 66 = 0
коэффициенты p и q выходят за пределы шкалы, выполним подстановку
z = 5t, получим уравнение t2 - 5t + 2,64 = 0, которое решаем посредством номограммы и получим t1 = 0,6 и t2 = 4,4, откуда z1 = 5t1 = 3,0 и z2 = 5t2 = 22,0.
9 способ: Геометрический способ решения квадратных уравнений
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал - Хорезми.
Примеры.
1) Решим уравнение х2 + 10х = 39.
В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39» (рис. 7).
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата, сторона каждого их них 2,5, а площадь 6,25.
Рисунок 7 - Квадрат и десять корней равны 39
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х2, четырех прямоугольников (4 • 2,5х = 10х) и четырех пристроенных квадратов (6,25 • 4 = 25), т.е. S =х2 + 10х + 25. Заменяя
х2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
А вот, например, как древние греки решали уравнение у2 + 6у - 16 = 0.
Решение представлено на рис. 16, где у2 + 6у = 16, или у2 + 6у + 9 = 16 + 9.
Решение. Выражения у2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у2 + 6у - 16 + 9 - 9 = 0 - одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2, у2 = - 8 (рис. 8).
Рисунок 8 - Геометрическое решение уравнения у2 + 6у - 16 + 9 - 9 = 0
3) Решить геометрически уравнение у2 - 6у - 16 = 0.
Преобразуя уравнение, получаем у2 - 6у = 16.
На рис. 9 находим «изображения» выражения у2 - 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у2 - 6у прибавить 9, то получим площадь квадрата со стороной у - 3. Заменяя выражение у2 - 6у равным ему числом 16,
получаем: (у - 3)2 = 16 + 9, т.е. у - 3 = ± √25, или у - 3 = ± 5, где у1 = 8 и у2 = - 2.
Рисунок 9 - Геометрическое решение выражения у2 - 6у
2.2. Как реализуется метод решения квадратных уравнений на компьютере.
Алгоритм решения данной задачи сначала должен быть представлен в виде словесного описания или графически в виде блок-схемы. Алгоритм вычисления корней квадратного уравнения может быть представлен в виде блок схем, изображенных на следующих рисунках:
Изображение алгоритма в виде блок-схемы позволяет наглядно представить последовательность действий, необходимых для решения поставленной задачи, убедиться самому программисту в правильности понимания поставленной задачи.
После разработки алгоритма решения задачи и представления его в виде блок-схемы можно перейти к написанию программы – последовательности инструкций на выбранном языке программирования, соответствующей разработанному алгоритму. Например, ниже приведен фрагмент программы решения квадратного уравнения, соответствующий приведенному снизу алгоритму, составленному на языке Turbo Pascal [5].
Рисунок 10 - Блок-схема алгоритма вычисления корней квадратного уравнения
if a=0 then
if b=0 then
if c=0 then
write (‘х – любое’)
else
write (‘нет решений)
else
write (‘x=’, - b/c)
else
begin
D: = b^b-4*a*c;
if D
write (‘нет решений’)
else
if D=0 then
write (‘x=’, - b/2*a)
else
write (‘x=’, (-b+sqrt(D))/(2*a), ‘или х=’, (-b-sgrt(d)/(2*a))
end.
НО программа, написанная на языке программирования состоит из инструкций, понятных человеку, но не понятных процессору компьютера. Поэтому чтобы процессор смог выполнить работу в соответствии с инструкциями исходной программы, она должна быть переведена на язык команд процессора то есть машинный язык. Задачу преобразования исходной программы в машинный код выполняет специальная программа - компилятор. Помимо преобразования исходной программы в машинную, компилятор выполняет проверку правильности записи инструкций исходной программы, т. е. осуществляет синтаксический анализ.
Рисунок 11 – Схема работы компилятора
Компилятор создает исполняемую программу только в том случае, если в тексте исходной программы нет синтаксических ошибок. Однако генерация исполняемой программы машинного кода свидетельствует только об отсутствии в тексте программы синтаксических ошибок. Убедиться в правильности работы программы можно только во время ее тестирования – пробных запусках программы и при анализе полученных результатов. Например, если в программе нахождения корней квадратного уравнения допущена ошибка в записи выражения вычисления дискриминанта, то даже если это выражение будет синтаксически верно, программа выдаст неверные значения корней.
Решение квадратных уравнений средствами TURBO Pascal[5]
Задача: Дано квадратное уравнение общего вида: ax2 + bx + c = 0. Ввести в память компьютера числовые коэффициенты: a, b, c, выполнить необходимый анализ введенной информации согласно известному из курса средней школы алгоритму решения квадратного уравнения: найти дискриминант
d=b2-4ac и, проанализировав его знак, найти все действительные корни, если знак дискриминанта положительный, или сообщить о том, что действительных корней нет, если знак дискриминанта отрицательный.
program q1;
║uses crt;
║var a, b, c, x1, x2, D: real;
║begin;
║read (a, b, c);
║write ('a=',a); write ('b=',b); write ('c=',c) ;
║D:=b*b-4*a*c;
║if Dкорней нет') else;
║if D0 then writeln ( 'x1=',(-b+sqrt(D))/(2*a)); writeln ('x2=', (-b-sqrt(D));
║else writeln ('x1=x2=', -b/(2*a));
║readkey;
║end.
Решение квадратных уравнений в Eхcel [5].
Набор таблицы.
В ячейку А1 набираем фразу «Решение квадратного уравнения вида Ах2+Вх+С=0», и выделяем ячейки строки А от 1 до той которая находится перед пунктирной линией. Форматируем расположение, начертание и размер букв через опцию ЯЧЕЙКИ меню ФОРМАТ. В подпанели Выравнивание устанавливаем значение «Центрировать по выделению». В подпанели Шрифт - размер и начертание букв (у нашем варианте это полужирный курсив и размер 14). Устанавливаем курсор на ячейке В4 и набираем А=, в ячейке В5 - В=, в ячейке В6 - С=, и производим форматирование по описанному выше методу. Ячейки С4, С5 и С6 выделяем рамкой в подпанели Рамка панели ЯЧЕЙКИ меню ФОРМАТ. Эти ячейки предназначены для ввода в них значений А, В, С.
Набор формулы. В ячейках Е4 и Е6 пишем соответственно х1= и х2=, и форматируем по методу, описанному выше. А в ячейки F4 и F6 записываем формулы так. Сначала ставится равно, потом значение ячейки В5 нажатием на ней мышки, функция Корень вставляется из пункта меню ВСТАВКА - ФУНКЦИЯ... Выбираем из математических функций - КОРЕНЬ. И нажимаем кнопку Далее - для ввода значения, находящегося под корнем. Следуя формуле дискриминанта вводим B5^2-(4*B4*B6), а общий вид формулы - =(-B5 + КОРЕНЬ(B5^2-(4*B4*B6)))/(2*B4) Такую же формулу вставляем и в ячейку F6, но со знаком минус: =(-B5 - КОРЕНЬ(B5^2-(4*B4*B6)))/(2*B4) Теперь после ввода пользователем значений А, В,С в ячейки В4, В5 и В6, в ячейках F4 и F6 будут выводится соответственно значения х1 и х2.
Рисунок 12 - Решение квадратных уравнений в Eхcel вида Ax^2+Bx+C=0
Решение квадратных уравнений в программе «AdvancedGrapher» [5]
Рисунок 13 - График второй зависимости – прямая в программе «AdvancedGrapher»
Если в уравнении х2 + px + q = 0 перенести второй и третий члены в правую часть, то получим х2 = - px - q.
Построим графики зависимости у = х2 и у = - px - q.
График первой зависимости - парабола, проходящая через начало координат. График второй зависимости - прямая (рис. 13). Все данные вводим в программу «AdvancedGrapher» и получаем ответы [5].
Искомая окружность пересекает ось абсцисс в точках B (х1 ; 0) и D (х2 ; 0), где х1 и х2 – корни уравнения ах2 + bх + с=0, и проходит через точки А (0;1) и С (0;) на оси ординат [4, c. 34].
Возможны следующие случаи:
- прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
Рисунок 14 - Решение графически уравнения х2 - 3х - 4 = 0 в программе «AdvancedGrapher»
- прямая и парабола могут касаться (только одна общая точка), т.е. уравнение имеет одно решение;
- прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
Примеры.
1) Решим графически уравнение х2 - 3х - 4 = 0 (рис. 14).
Решение. Запишем уравнение в виде х2 = 3х + 4.
Построим параболу у = х2 и прямую у = 3х + 4. Прямую у = 3х + 4 можно построить по двум точкам М (0; 4) и N (3; 13). Прямая и парабола пересекаются в двух точках А и В с абсциссами х1 = - 1 и х2 = 4.
Ответ: х1 = - 1; х2 = 4.
Рисунок 15 - Решение графически уравнения х2 - 2х + 1 = 0 в программе «AdvancedGrapher»
2) Решим графически уравнение (рис. 15) х2 - 2х + 1 = 0.
Решение. Запишем уравнение в виде х2 = 2х - 1.
Построим параболу у = х2 и прямую у = 2х - 1.
Прямую у = 2х - 1 построим по двум точкам М (0; - 1)
и N(1/2; 0). Прямая и парабола пересекаются в точке А с абсциссой х = 1. Ответ: х = 1.
Рисунок 16 - Решение графически уравнения х2 - 2х + 5 = 0 в программе «AdvancedGrapher»
3) Решим графически уравнение х2 - 2х + 5 = 0 (рис. 16).
Решение. Запишем уравнение в виде х2 = 5х - 5. Построим параболу у = х2 и прямую у = 2х - 5. Прямую у = 2х - 5 построим по двум точкам М(0; - 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.
Ответ. Уравнение х2 - 2х + 5 = 0 корней не имеет.
Нахождение корней квадратного уравнения с помощью
логических функций. [5]
В ячейку А1 набираем фразу «Решение квадратного уравнения вида Ах2+Вх+С=0»,
В ячейку А2 записываем А=, А3 – В=, в А4 – С=. Ячейки В2. В3, В4 выделяем рамкой.
В ячейки D2, D3, D4 записываем соответственно D=, x1=, x2=.
Напишем формулу для подсчета дискриминанта в информатике =В3*В3+4*В2*В4.
Рисунок 17 - Формула для подсчета дискриминанта в информатике =В3*В3+4*В2*В4 с помощью логических функций
Теперь запишем формулы, используя функцию “ЕСЛИ”:
Для X1: =ЕСЛИ(E20;(-B3-КОРЕНЬ(E2))/(2*B2);ЕСЛИ(E2=0;-(B3)/(2*B2); «корней нет»)) Для X2: =ЕСЛИ(E20;(-B3+КОРЕНЬ(E2))/(2*B2);ЕСЛИ(E2=0;-(B3)/(2*B2); «корней нет»))
Рисунок 18 - Формула, используя функцию «ЕСЛИ»:
Решение квадратного уравнения x2-2x+1=0
Решение квадратного уравнения x2-2x+1=0 с помощью
логических функций отображено на рисунке 19.
Рисунок 19 - Решение квадратного уравнения x2-2x+1=0 с помощью
логических функций
Решение уравнения х2-5х+6=0.
Рисунок 20 - Решение уравнения х2-5х+6=0 с помощью логических функций
Нахождение корней квадратного уравнения с помощью
средства «Поиск решения» [5].
Команда Подбор параметра является удобной для решения задач поиска определенного целевого значения, зависящего от одного неизвестного параметра. Для более сложных задач следует использовать команду Поиск решения (Решатель), доступ к которой реализован через пункт меню Сервис/Поиск решения.
Рассмотрим, как воспользоваться Поиском решения на примере того же квадратного уравнения.
После открытия диалога Поиск решения (рис. 21) необходимо выполнить следующие действия:
1) в поле Установить целевую ячейку ввести адрес ячейки, содержащей
формулу для вычисления значений оптимизируемой функции, в нашем примере целевая ячейка – это С4, а
формула в ней имеет вид: = C3^2 - 5*C3 + 6;
2) для максимизации значения целевой ячейки, установить переключатель максимальному значению в положение  , для минимизации используется переключатель минимальному значению, в нашем случае устанавливаем переключатель в положение значению и вводим значение 0;
, для минимизации используется переключатель минимальному значению, в нашем случае устанавливаем переключатель в положение значению и вводим значение 0;
3) в поле Изменяя ячейки ввести адреса изменяемых ячеек, т. е. аргументов целевой функции (С3), разделяя их знаком «;» (или щелкая
мышью при нажатой клавише Сtrl на соответствующих ячейках),
для автоматического поиска всех влияющих на решение ячеек используется кнопка Предположить;
4) в поле Ограничения с помощью кнопки Добавить ввести все ограничения, которым должен отвечать результат поиска: для нашего примера ограничений задавать не нужно;
5) для запуска процесса поиска решения нажать кнопку Выполнить.
Рисунок 21 - Нахождение корней квадратного уравнения с помощью
средства «Поиск решения»
Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения.
Заключение
Подводя итоги, можно сделать вывод, что квадратные уравнения играют огромную роль в развитии математики. Не менее важно и то, что в результате применения квадратных уравнений при решении задач не редко обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений. Хочется отметить и то, что излагаемая тема в этой работе еще мало изучена, поэтому она таит в себе много скрытого и неизвестного, что дает прекрасную возможность для дальнейшей работы над ней. Здесь мы остановились на вопросе решения квадратных уравнений, а что, если существуют и другие способы их решения?! Опять находить красивые закономерности, какие-то факты, уточнения, делать обобщения, открывать все новое и новое. Но это вопросы уже следующих работ. В результате изучения новых способов решения квадратных уравнений мы получили возможность решать уравнения не только по формуле, но и более интересными способами. Решил множество уравнений, изучили программы «TURBO Pascal», «Eхcel» и «AdvancedGrapher»[5].Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт. Данная исследовательская работа может быть использована учителями математики на уроках и элективных курсах по математике при изучении темы «Квадратные уравнения» (Приложения А-В), студенты для расширения и углубления знаний по решению квадратных уравнений. Любой учащийся, используя эту исследовательскую работу, может самостоятельно изучить данную тему (Приложения А-Б).
Так как эти методы решения квадратных уравнений просты в применении, то они, безусловно, должны заинтересовать увлекающихся математикой студентов, всё это нам даёт возможность по-другому посмотреть на те задачи, которые ставит перед нами математика.
Цель работы достигнута, задачи, поставленные в начале исследования, выполнены.
Список литературы
Брадис, В.М. Четырехзначные математические таблицы для средней школы. 23-е. изд./ В.М. Брадис / - М.: Просвещение, 2020. - 93 с.
Глейзер, Г.И. История математики в школе. 7-8 классы. / Г.И. Глейзер/ – М.: Просвещение, 2017. - 158 с.
Методические рекомендации по выполнению индивидуального проекта для обучающихся ГБПОУ ШКАИ / Сост. О. В. Воронцова, 2020. – 52 с.
Окунев, А.К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. / А.К. Окунев / - М.: Просвещение, 2016. - 130 с.
Программы «TURBO Pascal», «Eхcel» и «AdvancedGrapher».
Приложение А
Что необходимо знать для решения квадратных уравнений?
О чем надо помнить решая квадратные уравнения?
Рисунок А.1 - Медоты решения полных квадратных уравнений
Рисунок А.2 - Методы решения приведенных квадратных уравнений.
Рисунок А.3 - Методы решения неполных квадратных уравнений
Рисунок А.4 - Методы решения уравнений, сводящихся к квадратным
Рисунок А.5 - Корни квадратного уравнения и дискриминант
Распознание корней
| Знаки коэффициентов | Знаки корней |
| A0 | B0 | C | Разные: больший отрицателен |
| A0 | B | C | Разные: больший положителен |
| A0 | B0 | C0 | Одинаковые: оба отрицательные |
| A0 | B | C0 | Одинаковые: оба положительные |
Обобщенный приём алгебраического решения уравнений
Рисунок А.6 - Схема решения квадратных уравнений
Приём контроля решения уравнения алгебраическим способом
1. Проверить, правильно ли определён вид уравнения.
2. Проверить, приводят ли данное уравнение к простейшему выбранные тождественные и равносильные преобразования.
3. Проверить правильность выполнения преобразований.
4. Проверить применение правила (формулы, алгоритма) решения простейшего уравнения.
5. Проверить вычисления при проверке решения.
6. Проверить запись ответа.
Обобщение имеющихся знаний
о квадратных уравнениях и способах их решения
Рисунок А.7 - Общий вид квадратного уравнения
Рисунок А.8 - Полные уравнения
Рисунок 9.А - Полные уравнения с особым случаем
Рисунок 10.А - Неполные уравнения
Приложение Б
Нестандартные приемы решения квадратных уравнений
Рисунок 1.Б - Метод коэффициентов
Рисунок 2.Б - Уравнение вида ax2+(a2+1)x+a=0
Рисунок 3.Б - Уравнение вида ax2-(a2+1)x+a=0
Рисунок 4.Б - Уравнение вида ax2+(a2+1)x-a=0
Рисунок 5.Б - Уравнение вида ax^2-(a^2-1)x-a=0
Рисунок 6.Б - Приём «переброски» старшего коэффициента
Приложение В
Дидактический материал
по применению нестандартных приемов решения квадратных
уравнений.
1. Найди наиболее рациональным способом корни уравнения:
а) 4х2 – 13х + 9 =0 (1; 2,25)
б)1978х2 – 1984х + 6=0 (1; 6/1978)
в) 4х2 + 11х + 7 = 0 (-1; -7/4)
г) 319х2 + 1988х +1669=0 (-1; -1669/319)
д) 1999х2 + 2000х+1=0 (-1; -1/1999)
2. Решить квадратные уравнения с большими коэффициентами
а) 313х2 +326х+13=0 (-1; -13/313)
б) 839х2– 448х -391=0 (1; -391/839)
в) 345х2 – 137х – 208=0 (1;.-208/345)
г) 939х2+978х+39=0 (-1; -39/939)
3. Используя полученные знания, установи соответствие:
| 1)х2+5х+6=0
2)6х2-5х+1=0
3)2х2-5х+3=0
4)3х2-5х+2=0
5)х2-5х+6=0
6)6х2+5х+1=0
7)2х2+5х+2=0
8)3х2+5х+2=0 | 1)1/6;1/2
2)1;3/2
3)1;2/3
4)-2;-3
5)-1/3;1/2
6)-1;-3/2
7)-1;-2/3
8)-2;3 |
|
|
|
Анализ работы учащихся по решению квадратных уравнений нестандартными способами
Разработаны критерии оценки практикума:
За каждое верно выполненное задание ставится 1 балл;
Наиболее возможное количество набранных баллов-17
Если студент набирает:
Менее 7 баллов, то выставляется оценка «2»
от 7 до 11 баллов «3»
от 12 до 15 баллов «4»
от 16-17 баллов «5»
Результаты практикума.
Выполняли работу – 10 человек. Набрали баллов
От.16-17–8.человек.(80%)
От.12-15–2.человек.(20%)
Менее 12 – 0 человек.(0%)
Рисунок 1.В - График результатов практикума
Средний балл – 4,45. Процент качества – 100%
Типичные ошибки, допущенные в работе связаны с невнимательностью учащихся.
Выводы по результатам проведения практикума
Успешно выполненная работа студентов 170 группы, позволяет сделать следующие выводы:
Нестандартные приемы решения квадратных уравнений заслуживают внимания;
позволяют экономить время решения, что обусловлено применением тестовой системы экзаменов.






 (2)
(2) 1x2 = q,
1x2 = q,

 Согласно теореме Виета
Согласно теореме Виета (3)
(3)
 (5)
(5)
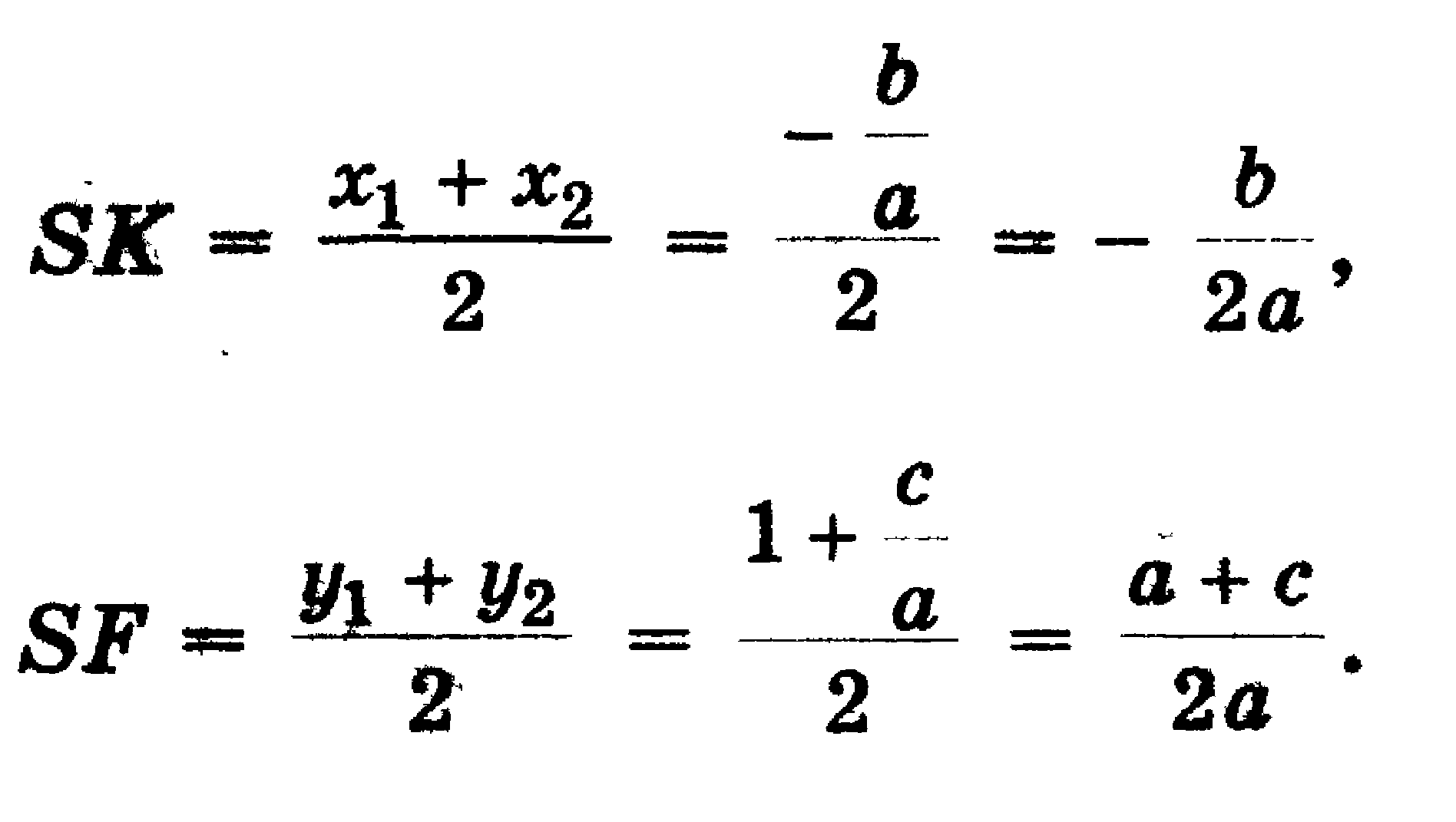



 (8)
(8) (9)
(9) (10)
(10)









