| 2-этап Жаңы тема | Окуучулар теманы китептен окуп чыгышат. Сабак боюнча түшүнүк алышып мисалдарды чыгарышат. Арифметикалык амалдар - бул берилген санга ылайыктуу шартты канааттандырган башка санды табуу ыкмасы. Мектеп арифметикасында натурал сандарды жана оң бөлчөлөрдү кошуу, кемитүү, көбөйтүү, бөлүү каралат. Берилген натуралдык сандарды кошуу - ошол сандарда канча бирдик болсо, ошончо бирдиктен турган санды табуу ыкмасы. Берилген сандар кошумчалар, ал эми кошуунун натыйжасы сумма деп аталат. Мисалы, 5 + 7 + 8 = 20, бул жерде 5, 7, 8 бириктиргичтер, 20 суммалар. Кошуу ыкмасы коммутативдик (коммутативдик) жана агрегативдик (ассоциативдик) мыйзамдарга баш иет. Илгери сандар сол жактан кошулуп турган. Кошуунун кадимки ыкмасы, анын белгиси (+) 15-кылымда киргизилген. Чакыруу методу - бул берилген сумманы жана бир мүчөнүн экинчи мүчөсүн табуу ыкмасы. Берилген сумма азайтуучу, берилген сумма азайтуучу, ал эми чыгаруунун натыйжасы айырма деп аталат. Ошентип, алып салуу ыкмасы кошуу ыкмасына тескери болот. Мисалы, 15-8 = 7; 15 - редуктор, 8 - редуктор, 7 - айырма. Мурда кыскартуу методу, тескерисинче, сол тараптан башталган. Салттуу ыкма Европада 15-кылымдан бери колдонулуп келе жатат. Минус белгиси (-) пайда болгон убакыт - убакыт.Натуралдык сандарды көбөйтүү - бир эле компоненттердин суммасын табуу ыкмасы. Кошумча иретинде кайталанган сан мультипликатор, канча жолу кошулгандыгын көрсөткөн цифра, ал эми амалдын натыйжасы мультипликатор деп аталат. Көбөйткүчтөр жана көбөйткүчтөр көбүнчө көбөйткүч деп аталат. Мисалы, 6X5 = 30, 6 көбөйткүч болуп саналат. 5 - көбөйткүч, 30 - көбөйткүч. Көбөйтүү ыкмасы бири-бирине алмашуу, топтоо жана бөлүштүрүү мыйзамдарына баш иет. Байыркы Индияда көбөйтүү сол тараптан башталган. Салттуу ыкма 15-кылымдан бери колдонулуп келе жатат. Көбөйтүү белгиси алгач чекит (•) катары жазылган (15-кылым), андан кийин киргизүү (X) (17-кылым).Ошол факторлордун бири менен эки фактордун көбөйтүмүн табуу ыкмасы бөлүнүү деп аталат. Бөлүнүүчү сан бөлүүчү, бөлүнүүчү бөлүүчү, ал эми бөлүнүүнүн натыйжасы бөлүүчү деп аталат. Мисалы, 12: 3 = 4, 12 бөлүнөт, 3 бөлүнөт, 4 бөлүнөт. Бөлүү ыкмасы - көбөйтүү ыкмасына тескери. Бөлүү методу эки түргө бөлүнөт: бүтүндөй бөлүнүү жана калдык бөлүү. Калдыкка бөлүү, чыгарылышы берилген бөлүнгүчтөн ашпаган эң чоң бүтүн санды табууну билдирет. Бул сиз издеп жаткан номер деп аталат. Бөлүүчү менен бөлүүчүнүн көбөйтүндүсүнүн айырмасы бөлүкчөдөн ар дайым кичине калдык деп аталат. Мисалы, 21ди 4кө бөлгөндө, ал толук эмес 5ке, калганы 1, башкача айтканда, 21 = 4x5 + 1. Бөлүнүүнүн учурдагы ыкмасы 15-кылымда италиялык окумуштуулар тарабынан ойлоп табылган. Бөлүнүүнүн биринчи белгиси (:) (1633-жылы) англис окумуштуусу Джонсон болгон.Теңдиктин белгисин (=) киргизген биринчи англис дарыгери Роберт Рекорд (1557) болгон. Арифметикалык операциялардагы заманбап белгилер 17-кылымдын аягында гана бардык өлкөлөрдө колдонула баштаган. 1-деңгээл. Байланыш түзүү: 0110 + 0110 = 1101 + 0110 = 11001 + 10111 = 1010 + 0101 = 10001 + 01101 = 1000 + 1110 = 2-деңгээл. Кыскартууну жүргүзүңүз: 1010 - 110 = 1101 - 110 = 1001 - 111 = 1101 - 10 = 10001 - 1101 = 1000 - 101 = 3-деңгээл. Төмөнкү кадамдарды аткарыңыз: 1010 + 110 = 1011 - 101 = 1011 + 111 = 1001 - 11 = 10101 - 1101 =
| -
Түшүндүрүү процесси жүрөт. -
Билими жогорулайт -
Тема боюнча ой жүгүртүүсү өсөт. -
Көңүл буурусу жогорулайт. -
Айырмалап билүүгө үйрөнөт. -
Так маалыматтарды ажырата алат. -
Толук жыйынтык чыгарганга үйрөнүшөт. | НК1, НК2 | ПК1, ПК2 |
|








 омпьютердин эсинде информация экилик коддо – нөл жана бир чынжырчалары түрүндө берилет. Клавиатурадагы ар бир символго, сегиз – 0дєн жана 1ден турган – уникалдуу чынжырчалар туура келет. Мисалы, «Q» тамгасынын экилик коду 01010001, ал эми «7» саныныкы 00110111.
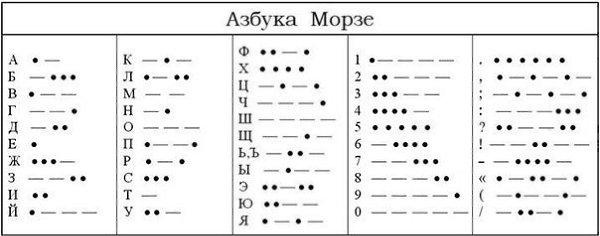
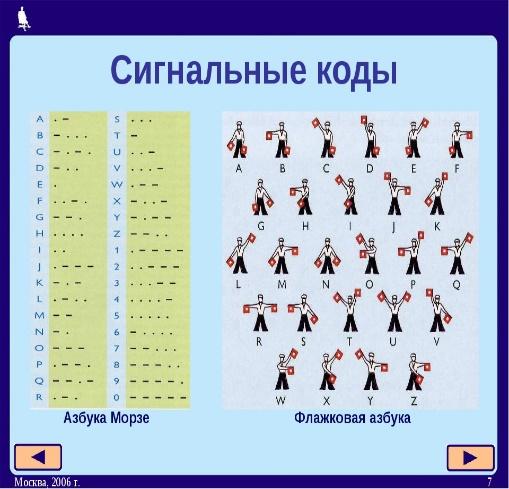
омпьютердин эсинде информация экилик коддо – нөл жана бир чынжырчалары түрүндө берилет. Клавиатурадагы ар бир символго, сегиз – 0дєн жана 1ден турган – уникалдуу чынжырчалар туура келет. Мисалы, «Q» тамгасынын экилик коду 01010001, ал эми «7» саныныкы 00110111.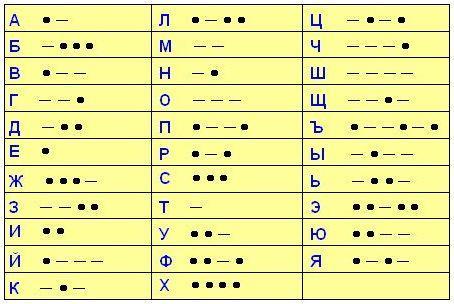 рзе коду, Морзе коду - шарттуу сигналдар тутуму. Морзе коду америкалык ойлоп табуучу Сэмюэл Морз (1791-1872) ойлоп тапкан аппаратка негизделген. Морзе коду менен билдирүүлөрдү кодлоп, кагаз тасмага жаздырууга болот. [1] Морзе кодунда ар бир тамга же символ токтун импульсунун кыска мөөнөттүү (чекит) жана үч узун (тире) сигналдарынын белгилүү бир айкалышына туура келет; алар чекиттин узундугуна барабар токсуз интервал менен бөлүнөт. Сөздөгү тамгалар жана көп орундуу сандар ар бир айкалышты аягына чыгарган үч эселенген ток эмес аралыгы менен, ал эми тексттеги сөздөр беш убакыттуу ток эмес аралыгы менен бөлүнөт. Морзе кодунда ар бир тамга байланыш линиясын жана батарейкага туташкан байланышты ачкыч менен туташтыруу аркылуу берилет.
рзе коду, Морзе коду - шарттуу сигналдар тутуму. Морзе коду америкалык ойлоп табуучу Сэмюэл Морз (1791-1872) ойлоп тапкан аппаратка негизделген. Морзе коду менен билдирүүлөрдү кодлоп, кагаз тасмага жаздырууга болот. [1] Морзе кодунда ар бир тамга же символ токтун импульсунун кыска мөөнөттүү (чекит) жана үч узун (тире) сигналдарынын белгилүү бир айкалышына туура келет; алар чекиттин узундугуна барабар токсуз интервал менен бөлүнөт. Сөздөгү тамгалар жана көп орундуу сандар ар бир айкалышты аягына чыгарган үч эселенген ток эмес аралыгы менен, ал эми тексттеги сөздөр беш убакыттуу ток эмес аралыгы менен бөлүнөт. Морзе кодунда ар бир тамга байланыш линиясын жана батарейкага туташкан байланышты ачкыч менен туташтыруу аркылуу берилет.