Информация о математиках

Составитель :Яралиева Р.А

А

Для древних историков Архимед, прежде всего, инженер,

специалист по фортификации, конструктор удивительных

военных машин. С помощью этих машин он успешно защи-

щал родной город Сиракузы от самой сильной в то время

армии - римской. На сухопутные войска римлян с шумом и

невероятной быстротой сыпались камни огромной величи-ны и веса тяжелые балки, загнутые на конце в виде журавлиных клювов, поднимали корабли высоко в воздух, а затем опускали в воду и так топили. Лишь через два года римлянам удалось взять город. Легенды рассказывают, что когда солдаты ворвались в город, Архимед был занят решением задачи и что-то чертил. Римский воин приказал ему встать, но старый ученый не повиновался, сказав, что хочет закончить решение. Тогда римлянин выхва-тил меч и убил Архимеда.

Но не только выдающимся инженером был Архимед, он прославился и своими математическими работами. Древние ученые разных стран пытались вычислить длину окружности и площадь круга. В работе "Об измерении круга" Архимед доказал, что 3/1071 π π 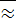_{ }3,14. Этим значением π мы пользуемся до сих пор.

У древних греков имелась собственная нумерация, которая была не очень удобной для записи больших чисел. В работе "Исчисление песчинок" Архи-мед разработал метод, позволяющий записать числа, превышающие число песчинок внутри сферы диаметра равного расстоянию между центром Зем-ли и небесным сводом. Представьте себе, какой величины эти числа!

Но сам Архимед своим наиболее важным достижением в геометрии счи-тал сочинение "О шаре и цилиндре", в котором доказал, что объем шара, вписанного в цилиндр, в полтора раза меньше объема этого цилиндра и что отношение поверхности описанного цилиндра к поверхности вписанного шара также равно 3:2. Работы Архимеда по вычислению площадей и объемов - вершина греческой математики.

Что же мы знаем об Архимеде как человеке? Увы, не так много. Известно, что ученый жил на юге острова Сицилия в городе Сиракузы в III веке дон.э. Предполагают, что учился в Александрии Египетской состоял в переписке с тамошними учеными. С именем Архимеда связывают открытие законов рычага, разработку основ гидростатики, введение понятия центра тяжести.

Творения великого Архимеда не забыты и всегда будут вызывать восхищение всех, соприкасающихся с красотой греческой науки.

Карл Фридрих Гаусс

Гаусса нередко называют наследником Эйлера. Они оба носили нефор-мальное звание "король математиков" и удостоились посмертной уважи-тельной шутки: "Он перестал вычислять и жить". Их родным языком был немецкий, но научные труды оба предпочитали писать по латыни. Впрочем, Гаусс оказался последним латинистом среди крупных ученых Европы.

Он с гордостью ощущал себя питомцем эпохи Просвещения. Действи-тельно, в какую иную эпоху талантливый сын садовника и водопроводчика мог удостоиться персональной стипендии от герцога Брауншвейгского и быть принятым в Геттингенский университет? Этот долг Гаусс вернул ро-дине с лихвой: математическая школа в Геттингене сделалась сильнейшей в Германии и процветала более ста лет - пока к власти не пришел Гитлер.

Математический талант Гаусса проявился в раннем детстве - и конечно, первым его увлечением стала арифметика. В 9 лет он открыл (во время школьного урока) формулу суммы арифметической прогрессии. Позднее Гаусс перенес все теоремы арифметики натуральных чисел на многочлены и на целые комплексные числа. Позднее ученик Гаусса - Петер Дирихле - намного превзошел учителя, доказав, что в любой арифметической прогрессии содержится бесконечное множество простых чисел (если первый член и разность этой прогрессии взаимно просты).

Гаусс до старости сохранил юношескую жажду знаний и огромное любо-пытство. Например, в 62 года он быстро выучил русский язык, чтобы само-му разобраться в трудах своего коллеги - Николая Лобачевского. Но обыч-но Гаусс избегал читать чужие статьи или книги. Ему хватало формули-ровки основного результата; доказательство он придумывал сам, заодно открывая многие факты, о которых не подумал сам автор. Такая привычка оформилась в юности - когда 19-летний Гаусс решил сам освоить все достижения и методы алгебры, не пропуская ни одного яркого приложения этой древней науки.

Гауссу удалось построить правильный 17-угольник. Он завещал изобразить эту фигуру на своем надгробии - что и было сделано.

К 24 годам Гаусс вошел в число самых известных математиков Европы. Но для полной славы нужно было отличиться в области небесной механи-ки; тут судьба подбросила Гауссу достойную задачу. В первую ночь 1801 года астрономы обнаружили на небе малую планету Цереру, чья траектория лежит между Марсом и Юпитером. После немногих наблюдений планета была потеряна, и астрономы обратились за помощью к математикам. Гаусс первым откликнулся на этот призыв: по трем наблюдениям он сумел предсказать все будущие положения Цереры. Полвека спустя теория возму-щений Гаусса позволила астрономам рассчитать положение на небе еще никем не виданной планеты - Нептуна.

Занимался Гаусс и математической физикой: он строил математическую теорию магнетизма, в то время как в Англии Фарадей изобретал способы технического использования этой природной силы.

Не забывал Гаусс и о комплексных числах, которые так славно помогли ему разобраться в тайнах геометрических построений. Как будто развлекаясь, одинокий мудрец придумывал все новые доказательства своей теоремы о том, что всякий многочлен имеет комплексный корень. Видимо, Гаусс хотел понять: имеет ли эта "чисто алгебраическая" проблема хоть одно чисто алгебраическое решение, или неизбежны комбинации алгебры с геометрией, либо с математическим анализом? Оказалось, что такие комбинации неизбежны. Любая сложная проблема решается лишь после нескольких ее переводов с одного математического языка на другой. И вот уже два столетия вся математическая наука развивается в режиме взаимо-помощи и сплетения ее различных ветвей. Гаусс первым начал работать в таком режиме: как бы перебрасывая горящий уголек из одной ладони в другую. За это его называют "отцом современной математики".

Н.И. Лобачевский (1792-1856)

В ноябре 1802 г. после смерти мужа Прасковья Александровна подала прошение в Казанскую гимназию о приеме в нее трех своих сыновей — Александра одиннадцати лет, Николая девяти лет и Алексея семи лет, и вместе с сыновьями переехала из Нижнего Новгорода в Казань. Все три мальчика были приняты в гимназию на казенное содержание. Режим и быт в гимназии были очень суровыми и тяжелыми. Лобачевский и его братья были предоставлены гимназическим воспитателям и самим себе; не изба-лованные жизнью дома, они легче других переносили трудные условия жизни в гимна-зии. Тяжелее других переносил суровый режим Николай, он не любил подчиняться и поэтому иногда энергично проявлял свой характер. Тем не менее, Николай Лобачевский аттестовался «весьма прилежным и благонравным» и «занимающимся с особенным прилежанием математикой и латинским языком».

Братья Лобачевские Николай и Алексей окончили Казанскую гимназию в 1807 г. и были зачислены в Казанский университет с письменного согласия их матери Прасковьи Александровны. В первый год занятий в университете преподавание математики было поручено двум студентам, но Николай знал математику лучше них и поэтому некоторое время он занимался медициной. Лобачевский уже в начале занятий в университете свободно читал научные мемуары на латинском, немецком и французском языках, хотя то время ему было всего 15 лет. В университете Лобачевский получил энциклопедии-ческое образование. Он изучил свыше тридцати научных дисциплин по всем матема-тическим, прикладным, языковым, историко-философским и другим наукам, получил углубленное специальное образование. 3-го августа 1811 года Лобачевский был утверж-ден в звании магистров.

В 1814 г. Лобачевскому и Симонову были присвоены звания адъюнктов физико-ма-тематических наук; в возрасте 21-го года Лобачевский становится преподавателем уни-верситета и получает назначение на чтение лекций по тригонометрии и теории чисел.

В мае 1827 г. Лобачевский был избран ректором Казанского университета, и эту должность он занимал 19 лет. В течение почти 35-ти лет преподавания в университете Лобачевский читал арифметику и геометрию, алгебру элементарную и высшую, прямо-линейную и сферическую тригонометрию, аналитическую и начертательную геомет-рию, дифференциальное, интегральное и вариационное исчисления, вычисление прира-щений, исчисление вероятностей, теорию чисел, физику опытную и математическую, теоретическую механику, гидростатику и гидравлику, астрономию теоретическую и физическую, геодезию и топографию, уравнения в частных производных первого и второго порядков. Вряд ли можно назвать другого профессора, научные и преподава-тельские интересы которого охватывали бы такое множество учебных дисциплин. Программы Лобачевского содержали все важнейшие разделы точного знания, которые были глубоко изучены и продуманы и преподавались студентам в обстоятельном и систематическом изложении.

Лобачевский постоянно следил за современной ему новой научной литературой во всех областях математических знаний, поэтому студенты получали образование, соот-ветствующее высокому уровню современной европейской науки. Лекции Лобачевского были увлекательны, содержали глубокие мысли, он читал их не торопясь, очень убеди-тельно, так что материал лекций усваивался без особых затруднений и его легко было записывать. Формулы и чертежи выписывались на доске красиво и четко, чтобы студенты испытывали удовольствие от предмета преподавания.

Фалес (624-547 гг. до н.э)

Фалес считается одним из семи мудрецов, оказавших большое влияние на жизнь древних греков. И это первый древнегреческий мыслитель, имя которого дошло до нас. Его основная деятельность связана с городом Милетом в Малой Азии. По имени род-ного города его стали называть Фалес Милетский. Население там было неоднородным, много было греков, финикийцев, и некоторые историки утверждают, что Фалес происходил из зажиточной финикийской семьи. Долгие годы он провел по торговым делам в Египте и этим пребыванием воспользовался для получения от египетских жрецов доступа к высшим тайнам их науки, прежде всего, к математике и астрономии.

Временной период жизни Фалеса датируют 624-547 годами до н.э. Это подтверждается косвенными данными: известно, что Фалес предсказал полное солнечное затмение, которое произошло 28 мая 585 года до н.э. Отец истории Геродот рассказывает, что затмение случилось во время битвы между персами и войсками ионийских городов, в число которых входил и Милет. Воины были так напуганы, что не захотели продолжить битву. Пришлось договариваться о мире.

Но более всего Фалес известен тем, что ввел в геометрию доказательства. Вдумайтесь: убеждая людей в чем-то при помощи доказательств, человек обращается только к разуму, верит только в разум, что было в древности далеко не ординарным. Верили во что угодно и кому угодно: оракулу, жрецу, колдуну. Они казались существами особенными, наделенными благословением богов. Но чтобы обыкновенный смертный человек вдруг брался с уверенностью судить о том, чего нельзя непосредственно потрогать, — это было совершенно непостижимо! Можно назвать величайшие цивилизации, которые обогатили мир ценнейшими изобретениями и знаниями, но до доказательств так и не додумались.

Появление доказательств у Фалеса не должно нас удивлять. Ведь греки восприняли геометрические знания из Египта и Месопотамии. Но в массе геометрических фактов, накопленных ко времени Фалеса, попадались и противоречивые. Например, для вычисления площади круга в Месопотамии пользовались одним способом, а в Египте — другим. Причем не было никакой возможности восстановить ход мысли жрецов, которые когда-то получили эти результаты. Их рассуждения нигде не фиксировались, и их безнадежно забыли. Оценить факты, полученные его предшественниками, отделить верные знания от неверных было проще всего с помощью доказательства.

Фалес начал строить геометрию на логических основаниях, постепенно переходя при помощи доказательств от одного положения к другому. Ему принадлежит только начало этой системы, но ее продолжение оказалось настолько грандиозным, что можно говорить о Фалесе как о родоначальнике науки.

Три истории: История первая «О практической сметке»

Размышляя, главным образом, над вопросами устройства мира, философ почти не обращал внимания на обыденную жизнь. Однажды, например, засмотревшись в небо, он упал в ров. Такие события не могли не вызывать насмешек окружающих. Видевшая это некая прекрасная рабыня сказала, что Фалес хотел увидеть происходящее на небе-сах, но не заметил того, что находится у него под ногами. И однажды Фалес захотел доказать своим состоятельным друзьям, что у него тоже есть практическая сметка.

Он взял у них громадный кредит и скупил на эти деньги все маслодавильни в округе, поскольку предвидел хороший урожай оливок. А оливковое масло, будучи одним из основных продуктов питания в Древнем мире, служило еще и главным предметом экспорта, поэтому урожаи плодов оливковых деревьев регулярно приносили доход как мелким крестьянам, так и собственникам крупных оливковых рощ. Когда благоприят-ный прогноз оправдался, владельцам урожая ничего не оставалось делать, как везти свои оливки к «монополисту» Фалесу и платить за отжим масла хорошие деньги. Так философ не только вернул долг своим кредиторам , но и сам разбогател.

История вторая «Об измерении высоты пирамиды»

Египетские жрецы, желая испытать Фалеса, предложили ученому измерить высоту пирамиды. Он дождался, когда длина его собственной тени стала равна его росту, и в этот момент измерил длину тени, которую отбрасывала пирамида. Эта измеренная длина тени и равна высоте пирамиды.

История третья «Морская»

Рассказывают, что Фалесу принадлежит первое доказательство шарообразности Земли. Оно состоит в том, что человек, смотрящий в морскую даль, сначала замечает верхушку мачты приближающегося к берегу корабля, потом ее нижнюю часть и только в последнюю очередь видит сам корабль. Ситуация такая же, как будто объект выныривает из-за бугорка.

А как определить, на какое расстояние от наблюдателя, находящегося на суше, удален корабль, видимый в открытом море? Метод определения, применявшийся в те времена, был основан на признаке равенства треугольников по стороне и двум прилежащим углам, который, как известно, был доказан Фалесом.

Пусть наблюдатель находится на суше, в точке А, а корабль — в море, в недоступ-ной точке Б. Проведем к отрезку АВ перпендикуляр АС произвольной длины и разделим его пополам точкой!). Из точки С проведем перпендикуляр к отрезку АС, а затем проведем прямую BD до пересечения ее с этим перпендикуляром в точке Е. Треугольники EDC и BDA равны, а значит, равны и отрезки СЕ и АВ. Задача сводится к измерению на суше длины отрезка СЕ.

Эратосфен Киренский (ок. 276-194 до н. э.)

Эратосфен Киренский - греческий ученый и литератор, основатель физической географии; получил образование в Александрии и Афинах, занимался астрономией, филологией.

Эратосфен высчитал окружность Земли, а также определил дату Троянской войны (1194 -1184 до н. э.). Руководил Александрийской библиотекой и был воспитателем наследника престола, впоследствии Птолемея IV Филопатра.

Необычайно разносторонний, он занимался филологией, хронологией, математикой, астрономией, географией, сам писал стихи. Среди математических сочинений Эратос-фена нужно назвать произведение Платоник, представляющее род комментария к Ти-мею Платона, в котором рассматривались вопросы из области математики и музыки. Исходным пунктом был так называемый делийский вопрос, то есть удвоение куба. Геометрическое содержание имело произведение О средних величинах в 2 частях. В известном трактате Решето Эратосфен изложил упрощенную методику определения простых чисел (так называемое "решето Эратосфена").

В Географии в 3 книгах Эратосфен представил первое систематическое научное изложение географии. Он начал с обзора того, что было достигнуто греческой наукой в этой области на тот момент. Создал математическую и физическую географию. Он также высказал предположение, что если плыть от Гибралтара на запад, то можно до-плыть до Индии (это положение косвенным путем достигло Колумба и подсказало ему идею его путешествия). Эратосфен снабдил свое произведение географической картой мира. В трактате Об измерении Земли Эратосфен высчитал длину Экватора (итог: 252 тысячи стадий, то есть примерно 39 690 км, подсчет с минимальной ошибкой, посколь-ку истинная длина экватора составляет 40 120 км). В объемном произведении Хроно-графия в 9 книгах Эратосфен заложил основы научной хронологии. Оно охватывало период от разрушения Трои (1184/83 гг. до н. э.) до смерти Александра (323 г. до н э.). Эратосфен опирался на составленный им список олимпийских победителей и разра-ботал точную хронологическую таблицу, в которой все известные ему политические и культурные события датировал по олимпиадам (то есть, четырехлетними периодами между играми). Произведение древней комедии в 12 книгах было литературным, лингвистическим и историческим исследованием и решало проблемы подлинности и датировки произведений.

Однако самым известным достижением Эратосфена в области географии был изобретенный им способ измерения размеров Земли, изложению которого посвящен трактат Об измерении Земли. И хотя остается спорным, получилось ли у Эратосфена в итоге 250 000 стадий или 252 000, в любом случае этот результат замечателен - диаметр Земли оказался всего лишь на 80 км меньше, чем фактический полярный диаметр. В этой же работе были рассмотрены и астрономические задачи, такие, как оценка размера Солнца и Луны и расстояния до них, солнечные и лунные затмения.

Эратосфен был первым ученым, который назвал себя "филологом" (philologos - любящий науку, подобно тому как philosophos - любящий мудрость).

(1850 – 1891)

Русский математик, писательница, первая русская

женщина-профессор. Основные научные труды посвяще-

ны математическому анализу, механике и астрономии.

В 1888 году Парижская академия наук присуждала

премию за лучшую научную работу, посвященную дви-

жению твердого тела, имеющего одну неподвижную точку. Эту задачу называли также задачей о движении волчка - ведь все точки быстро вращающеегося волчка находятся в движении, за исключением конца острия, которым волчок касается пола. Издавна волчки (или, как их еще называют, юлы) были любимыми игрушками детей. Но они привлекали к себе внимание и солидных ученых - слишком удивительны были свойства вращающихся тел.

Выполненное исследование так понравилось членам жюри, что они решили увеличить сумму премии с 3000 франков до 5000 франков, Когда вскрыли конверт с именем автора, неожиданно оказалось, что самую лучшую работу написала единственная женщина, занимавшая в то время должности профессора математики, - Софья Васильевна Ковалевская.

ЗАГАДКИ о МАТЕМАТИКАХ

- Разгадал загадку круга,

Метод площадей нам дал,

Знаем мы, как в Сиракузах

Родину он защищал.

Свой народ спасал от бед,

Его имя ….. (Архимед).

- На острове Самос

Философ сей родился.

И во главу угла

Поставлены им числа.

И, говорят, за теорему

Принес богам быка он в жертву.

Был чемпионом Олимпиады,

Имел своих учеников.

Надеюсь, догадался каждый,

Что его имя ….. (Пифагор)

- Все, что раньше люди знали,

Он собрал в своих «Началах».

Было их 13 книг,

Написал их все …. (Евклид)

- Очень слабым он родился,

Но науке все ж сгодился.

Открыл не кто иной,

А он притяжения закон.

Интеграл дал миру он,

Физик Исаак….. (Ньютон)

- Математики начала

По обоям изучала

И влюбилась в ту науку.

Только вот какая штука.

Ведь в России в это время

Не пускали в вузы женщин.

Чтоб в математике достичь вершин,

Пришлось уехать девушке в Берлин,

И стать для этого фальшивою невестою,

Такой мы знаем Софью……. (Ковалевскую).