Интегрированный урок физики и информатики. Использование информационных технологий на уроках физики в 11 классе.

Интегрированный урок физики и информатики. Использование информационных технологий на уроках физики в 11 классе.

Тема: Дифракция света.

Цель урока: 1. Научить учащихся объяснять явления дифракции света на основе зонной теории Френеля.

2. Показать, от чего зависит разрешающая способность микроскопов и телескопов.

Учебные

вопросы: 1. Дифракция волн.

2. Дифракция света.

3. Зоны Френеля.

4. Дифракционный предел разрешения оптических приборов.

5. Дифракционная решётка. Время: 45 минут.

Место: Кабинет информатики.

Материальное и методическое обеспечение: плакаты с зонами Френеля- 2 шт., компьютеры Pentium I (II) с программным обеспечением «ОТКРЫТАЯ ФИЗИКА 1.1» под ред. СМ. Козела, дифракционные решётки с линейками - 12 шт., источник света.

Ход урока. I. Организационный этап - 2 минут.

Общее знакомство с учащимися. Отметить отсутствующих, проверка внешнего состояния класса. Организация внимания.

П. Этап подготовки учащихся к активному и сознательному усвоению нового материала. - 3 минут.

Объявление темы, цели и задач урока.

Учебная проблема: Почему образуется светлое пятно (Пуассона) на экране, когда на пути распространения света находится непрозрачный экран ? Каким образом можно наблюдать тёмное пятно при прохождении света через маленькую щель?

Фронтальный опрос класса для повторения:

- Принцип Гюйгенса.

- Интерференция волн (определение).

- Необходимые условия возникновения интерференции света.

- Условие когерентности световых волн.

- Условия максимума и минимума интерференционной картины.

0

III. Усвоение новых знаний и проверка понимания учащимися нового материала. - минут.

Дифракция - изменение направления распространения волны, возникающее, когда волна встречает препятствие или проходит через отверстие. Степень изгибания волны зависит от размера препятствия или отверстия по сравнению с длиной волны А,. Чем меньше препятствие или щель, тем сильнее изгибается волна.

Опр. Дифракцией называют процесс огибания волнами препятствий, размеры которых сравнимы с длиной волны X.

Пример: распространение звука в лесу, в пространстве за препятствиями и т.д.

2. Дифракция света. - минут.

Опр. Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении у края препятствия. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии появляется система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране появляется система параллельных дифракционных полос.

Теория дифракционных явлений была создана французским физиком Френелем в 1818 г. на основе волновых представлений. Френель дополнил принцип Гюйгенса идеей об интерференции вторичных волн. Это позволило выполнить расчет дифракционных картин от различных простых препятствий.

Дифракционная теория была построена на основе понятия зон Френеля. Для круглых препятствий радиус r_m кольцевых зон Френеля равен

r_m = yfm*X*L ,

где X - длина световой волны, L - расстояние от препятствия до плоскости наблюдения. Результат дифракции сильно зависит от числа m зон Френеля, укладывающихся на препятствии (r_m=R)

m=R²/(X*L).

0

При нечетном числе m в центре дифракционной картины при дифракции на круглом отверстии наблюдается светлое пятно, при четном m - темное.

При дифракции на круглом диске (или шарике) в центре дифракционной картины всегда наблюдается светлое пятно (пятно Пуассона).

При дифракции на линейных препятствиях ширины d характер дифракционной картины также зависит от числа m полоскообразных зон Френеля, определяемого соотношением

m=(d/2)²/(X*L).

Число зон Френеля, укладывающихся на препятствии, однозначно характеризует вид дифракционной картины. Это позволяет моделировать дифракционные явления, используя волны другой области спектра и выбрав соответствующие геометрические размеры установки. Так, например, можно моделировать дифракцию радиоволн с помощью света.

На компьютере посмотреть интерференцию от круглого экрана, отверстия, примой щели, иголки. Посмотреть как меняется дифракционная картина при изменении значения Я и размеров препятствий. Учащиеся должны сделать обобщение опытов.

3. Зоны Френеля. - 6 минут. Зоны Френеля (вид сбоку и спереди)

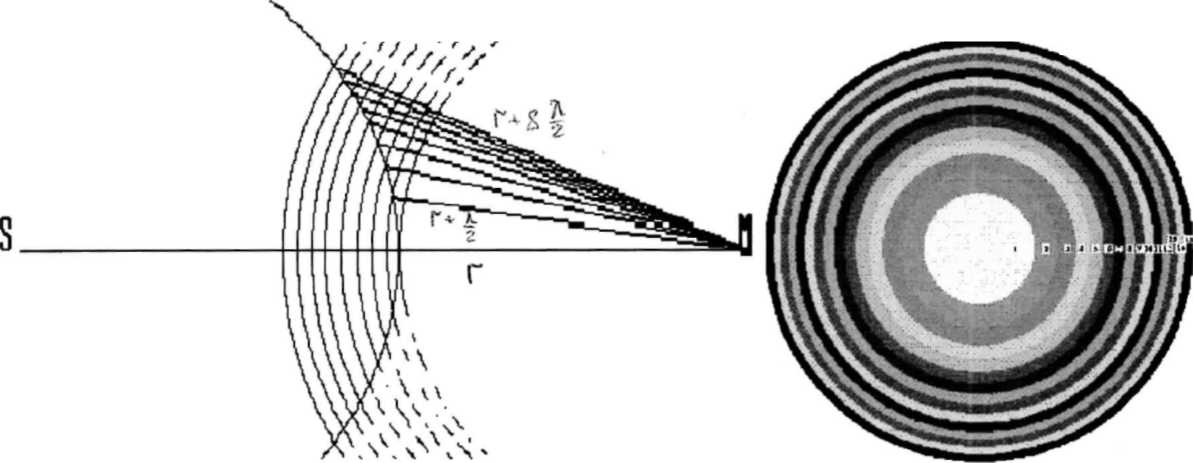
Для объяснения основных законов распространения света вблизи препятствий (отверстия, щели, непрозрачные диски) Френель дополнил принцип Гюйгенса постулатом об интерференции вторичных волн, приходящих в точку наблюдения от разных участков первоначального волнового фронта, не закрытых непрозрачными экранами. Этот новый постулат получил название принципа Гюйгенса-Френеля.

На основе принципа Гюйгенса-Френеля можно решить целый ряд дифракционных задач и рассчитать дифракционные картины от различных

0

препятствий. Одной из простых задач является дифракция на круглых отверстиях или круглых дисках. Если точечный источник света и точка наблюдения находятся на оси системы, то волновой фронт удобно разбивать на кольцевые зоны Френеля. Радиусы зон Френеля в плоскости экрана определяются выражением r_m = yjm*Я*L , где L - расстояние от экрана до плоскости наблюдения,

X - длина волны света.

Расчеты показывают, что площади зон Френеля одинаковы, (см. плакат №2). Поэтому амплитуды колебаний вторичных волн в точке наблюдения от каждой зоны одинаковы. Но колебания в точке Р, возбуждаемые соседними зонами, сдвинуты по фазе на тс, т.е. имеют разность хода Х/2.

Поэтому при увеличении размеров отверстия интенсивность света в центре дифракционной картины будет обращаться в ноль, если на отверстии укладывается четное число зон, и достигать максимума, когда число зон нечетное.

Если перекрыть непрозрачным экраном зоны Френеля через одну, то можно получить значительное усиление интенсивности колебаний в точке Р, так как колебания только от четных (или только от нечетных) зон происходят в одной фазе. Такие устройства называют зонными пластинками Френеля. Они действуют подобно линзе.

При дифракции света на круглом диске в центре дифракционной картины наблюдается светлое пятно {пятно Пуассона). Этот результат также может быть получен из теории зон Френеля.

Общий вид дифракционной картины при дифракции света на препятствиях круглой формы достаточно сложен. Он может быть найден для каждого положения точки наблюдения путем сложения колебаний от вторичных источников. Определение результатов интерференции вторичных волн является сложной математической задачей. Эта задача может быть решена с помощью компьютерного моделирования.

На компьютере посмотреть дифракцию от экрана, круглого отверстия когда на них помещаются чётное и нечётное число зон Френеля и сделать обобщение.

4. Дифракционный предел разрешения оптических приборов.

Если параллельный пучок света от удаленного точечного источника проходит через отверстие в непрозрачном экране, то вследствие дифракции пучок перестает быть параллельным; он испытывает дифракционное расширение. В фокальной

0

плоскости линзы, поставленной за экраном, изображение источника окажется размытым из-за дифракции. В случае круглого отверстия дифракционное изображение будет состоять из центрального светлого пятна и окружающих его концентрических колец.

Радиус центрального пятна в фокальной плоскости линзы равен: r=1.22*F*A,/D, где X - длина световой волны, D - диаметр отверстия, F - фокусное расстояние.

Если лучи света от удаленного источника падают на линзу непосредственно, то роль экрана выполняет оправа линзы. В этом случае под D нужно понимать диаметр линзы.

Дифракционное пятно уширяется при увеличении длины волны X и при уменьшении диаметра линзы D.

Дифракционный характер изображений ограничивает возможности оптических инструментов. Например, дифракционные изображения двух близких звезд в фокальной плоскости объектива телескопа могут сильно перекрыться, так что невозможно будет различить, наблюдаются две звезды или одна.

Если в объектив телескопа попадает свет от двух звезд, расположенных на угловом расстоянии , то в фокальной плоскости линзы диаметра D с фокусным расстоянием F центры дифракционных изображений звезд будут отстоять друг от друга на расстоянии (при малых углах ). Если это расстояние равно радиусу г центрального дифракционного пятна, то дифракционные картины сильно перекрываются, так что визуально трудно отличить изображение двух звезд от изображения одиночной звезды. В соответствии с этим условным критерием (критерий Релея) величина

называется дифракционным пределом разрешения линзы.

Аналогичным образом волновая природа света налагает предел на возможность различения близких деталей объекта, наблюдаемого в микроскоп.

На экране компьютера посмотреть как меняется дифракционные картины двойной звезды при изменении X и D.

5. Дифракционная решетка

0

_I

f

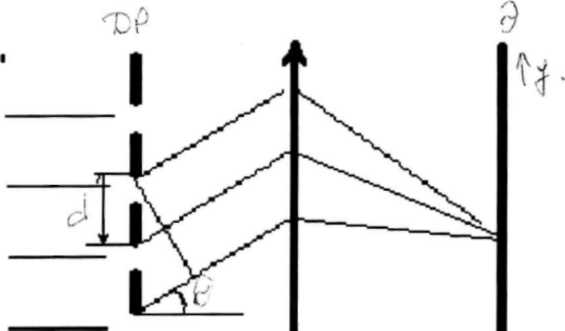
Простейшая дифракционная решетка представляет собой систему узких параллельных щелей, расположенных на одинаковом расстоянии друг от друга.

Если на решетку нормально падает монохроматический пучок света, то после решетки свет распространяется по нескольким направлениям. Если за решеткой поставить собирающую линзу, то в ее фокальной плоскости будут наблюдаться дифракционные максимумы различных порядков. Эти максимумы называются главными. Пучки света, образующие главные максимумы, распространяются после решетки в направлениях, определяемых формулой решетки:

^*sin#_m = т*X .

Здесь d - период решетки, - длина световой волны, m - целое число, называемое порядком дифракционного максимум .

Расстояние от максимума нулевого порядка (т=0) до максимума т-го порядка в фокальной плоскости линзы с фокусным расстоянием F при малых

Я

углах дифракции определяется формулой: у_т =т* — * F.

d

Так как положение максимумов (кроме нулевого!) зависит от длины волны, то решетка способна разлагать излучение в спектр, то есть она является спектральным прибором.

С помощью дифракционной решетки можно производить очень точные измерения длины волны. Если период решетки известен, то определение длины волн сводится к измерению угла , соответствующего направлению на выбранный максимум т-го порядка.

Если свет состоит из двух монохроматических волн с длинами волн Х\ и Х₂, то решетка в каждом спектральном порядке (кроме т=0) может отделить одну волну от другой.

IV. Закрепление нового материала. Задача.

На дифракционную решётку с периодом d= 2*10" см нормально падает монохроматический свет. Определите длину световой волны X, если угол между спектрами первого и второго порядка Дф=1°30'

(Ответ: 520 нм.)

V. Всестороняя проверка знаний. Фронтальный опрос.

VI. Подведение итогов урока.