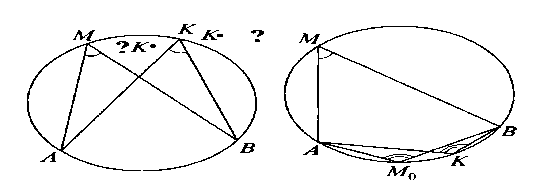Использование метода дополнительных построений при решении геометрических задач

Использование метода дополнительных построений при решении геометрических задач

Астахова Вера Григорьевна,

учитель математики МБОУ «Гимназия №3»

Большинство задач по геометрии, как планиметрических, так и стереометрических, не решаются по алгоритму, каждая требует своего подхода, но всё-таки можно при решении задач выделить общие идеи. Рассмотрим решение планиметрических задач. Решение геометрической задачи всегда начинается с построения чертежа, который выполняется с условием задачи, учитывается пропорциональность отрезков, углов, параллельности, перпендикулярности прямых и т.п. Аккуратное выполнение чертежа позволяет найти связь между элементами фигуры и наметить план решения. В ряде случаев решить задачу помогают дополнительные построения: отрезки, прямые, углы, треугольники, окружности и т.п. Дополнительные линии чаще всего проводятся для того, чтобы свести задачу к ранее решенной или просто более простой задаче, так как появляются другие фигуры, свойства которых известны учащимся, увеличивается число теорем, которые можно использовать. Метод дополнительных построений при решении геометрических задач является непростым, так как нужное дополнительное построение не всегда удается определить с первого взгляда. Иногда условие задачи подсказывает выбор дополнительного построения. Однако увидеть нужное дополнительное построение увидеть трудно. В одних случаях построения очевидны, в других требуют большого опыта того, кто решает задачу. Вместе с тем существуют достаточно типичные дополнительные построения, к выполнению которых учащихся можно подготовить. Для этого необходимо знать различные способы дополнительных построений, при которых решение геометрической задачи становится намного проще.

Приёмы дополнительного построения, которые используются при решении
геометрических задач можно разделить на два вида – это разбиение фигур и дополнение.
Разбиение фигур:

 проведение в многоугольнике прямой, параллельной одной из имеющихся (или
параллельных прямых), что позволяет применять подобие;

 разбиение фигуры на части с целью получения треугольника и параллелограмма (в том числе ромба, квадрата), что позволяет применять свойства этих фигур;

 проведение перпендикуляров, радиусов окружности в точки касания, высот в
трапеции позволяют получить прямоугольные треугольники.

Дополнение фигур:

 построение параллелограмма, с помощью продления медианы треугольника, что
позволяет применять свойства параллелограмма;

 построение дополнительного треугольника;

 построение вспомогательной окружности с целью применения свойств углов, хорд, касательных, связанных с окружностью.

Дополнительные построения встречаются по всему курсу планиметрии с 7 по 9 классы. В учебнике геометрии Л.С. Атанасяна имеются задачи, теоремы, при решении, доказательстве, которых применяются различные дополнительные построения, например, в темах: «Треугольники», «Параллельные прямые», «Соотношения между сторонами и углами треугольника», «Четырехугольники», «Площадь», «Подобные треугольники», «Окружность». В 7 классе вводится метод дополнительного построения при изучении темы «Свойства равнобедренного треугольника», при доказательстве признаков параллельности прямых, и теорем, обратных этим теоремам. В 8 классе при изучении темы «Четырехугольники», «Площади», «Теорема Пифагора» можно ознакомить обучающихся с удвоением медианы треугольника с последующим достраиванием треугольника до
параллелограмма, рассмотреть стандартные дополнительные построения в задачах на трапецию. При изучении планиметрии в 7-8 классах особое внимание
нужно уделять построению отрезков (соединение отрезком каких-либо точек, лежащих на
сторонах многоугольника, построение высот треугольника или четырехугольника,
радиусов или хорд окружности, диагоналей многоугольника, продолжение отрезков до
взаимного пересечения между собой и т.д.), при доказательстве теоремы о
сумме углов треугольника, неравенства треугольника. При этом общее представление о разновидностях дополнительных построений при решении геометрических задач у школьников не формируется, в учебниках нет систематизации разновидностей дополнительных построений.

Приведем некоторую квалификацию дополнительных построений.

1. Выделение элементов чертежа или фрагментальный чертеж.

Цель: более подробное рассмотрение нужной части чертежа.

1. Построение вспомогательной окружности, описанной около многоугольника.

Цель: получение вписанных, центральных углов, опирающихся на одну и ту же или равные дуги.

1. Построение боковых сторон трапеции до их пресечения.

Цель: получение треугольника и использование его свойств, использование замечательного свойства трапеции.

1. Удвоение медианы.

Цель: получение параллелограмма и использование его свойств.

1. Построение дополнительных прямых в треугольниках и многоугольниках, пересекающих их стороны или вершины, в частности, высот, медиан, биссектрис.

Цель: 1) получение равных ил подобных треугольников,

2) получение углов с соответственно параллельными или перпендикулярными сторонами,

3) перенос соотношений длин отрезков с одной стороны угла на другую.

1. Проведение дополнительных прямых в окружностях, в частности, радиусов, диаметров, хорд, секущих, касательных.

Цель: 1) получение вписанных и центральных углов,

2) получение углов между касательной и хордой,

3) использование теоремы о касательной и секущей.

Рассмотрим некоторые основные дополнительные построения, которые необходимо знать обучающимся.

Например, дополнительные построения в трапеции.

1) Проведение двух диагоналей.

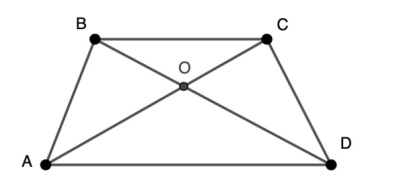
При проведении двух диагоналей образуются подобные треугольники, с которыми дальше можно работать.

В нашем случае это треугольники АОD и COB. В этих треугольниках можно отметить равные вертикальные углы, а также равные накрест лежащие углы при двух параллельных прямых AD и BC и секущей (на выбор берем одну из диагоналей).

2) Проведение двух высот.

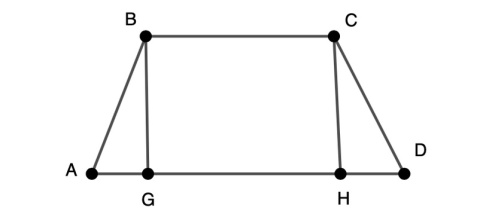
Проведя две высоты из вершин меньшего основания, мы делим трапецию на прямоугольник и два прямоугольных треугольника, имеющих одинаковые катеты (одинаковая высота трапеции).

Если такое дополнительное построение сделать в равнобедренной трапеции, то в этом случае мы получим два равных друг другу прямоугольных треугольника.

3) Продление боковых сторон до пересечения.

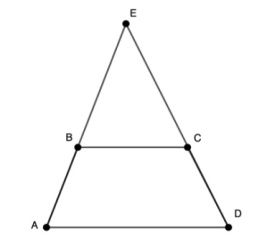
Продлеваем AB и DC до пересечения в точке Е. Если продлить боковые стороны до пересечения, мы получим треугольник, в котором проведена прямая, параллельная основанию.

За счет параллельных прямых мы снова получаем подобные треугольники (треугольники АЕD и BEC).

4) Из вершины малого основания внутри трапеции проводим прямую параллельно одной из боковых сторон.

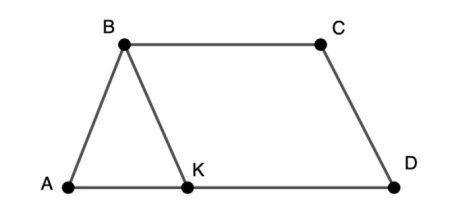
ВК параллельно CD. За счет параллельности мы отсекаем параллелограмм.

Особенно полезным данное дополнительное построение будет в том случае, когда мы знаем все стороны трапеции и нам необходимо найти какой-то угол в трапеции. Угол мы будем искать через теорему косинусов в треугольнике, который здесь образуется.

5) Из одной из вершин основания проводим прямую, параллельную одной из диагоналей до пересечении с прямой, которая содержит другое основание.

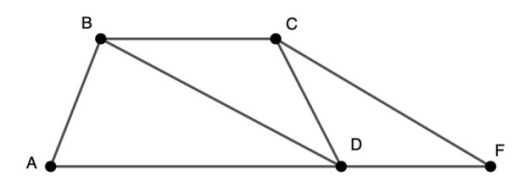
Проводим CF параллельно BD. Здесь мы также получаем параллелограмм, но дополнительно мы получаем сторону, которая равна сумме длин оснований исходной трапеции, что может пригодится в задачах на подобные идеи.

Построение вспомогательной окружности.

1. Если дан прямоугольный треугольник, то вокруг него описывается окружность,
   центром которой является середина гипотенузы.

2. Если дан четырехугольник, у которого суммы противоположных углов равны, то
   вокруг него описывается окружность. Признаком существования для четырехугольника
   описанной окружности обладают квадрат, прямоугольник и равнобедренная трапеция.

3. Если дан четырехугольник, у которого суммы противоположных сторон равны, то в него можно вписать окружность.

4. Если даны две окружности с общей внешней касательной, касающиеся друг друга
   внешним образом, то целесообразно рассмотреть треугольник, вершинами которого
   служат три точки касания данных фигур. Треугольник A₁AA₂ является прямоугольным с прямым углом А (А – точка касания окружностей).

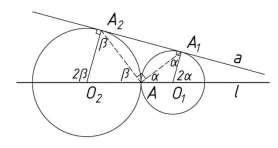
Вспомогательные окружности часто облегчают вычисление углов в задачах о
"некруглых" фигурах.

Теорема (условие принадлежности четырех точек окружности).

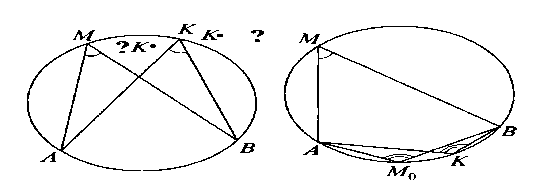
Если для четырех точек плоскости А, В, М, К выполняется одно из следующих условий:
а) точки М и К расположены по одну сторону от прямой АВ и при этом угол АМВ равен углу АКВ, то точки А, В, М и К лежат на одной окружности
б) точки М и К расположены по разные стороны от прямой АВ и при этом
АМВ + АКВ = 1800, то точки А, В, М и К лежат на одной окружности
Особенно важную роль играет частный случай.

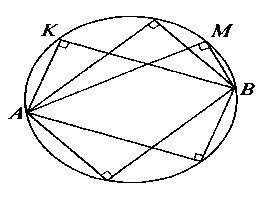
Теорема. Если АМВ = АКВ= 90⁰, то точки А, В, М, К расположены на окружности с диаметром АВ (здесь два случая слились в один: точки М и К могут располагаться как по одну, так и по разные стороны от прямой АВ)

Для примера рассмотрим решение геометрической задачи №16 ЕГЭ, где применяются дополнительные построения.

Задача. В трапеции АВСD боковая сторона АВ перпендикулярна основаниям. Из точки А на сторону СD опустили перпендикуляр АН. Точка Е принадлежит стороне АВ, прямые СD и СЕ перпендикулярны.

а) Докажите, что прямая ВН параллельна прямой ЕD.

б) Найдите отношение ВН к ЕD, если ВСD=150°.

Решение.

а) Докажем, что DЕА=НВЕ.

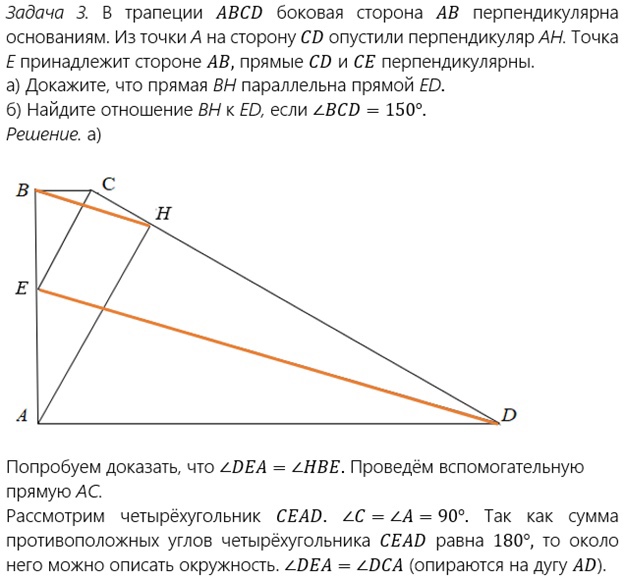
Для этого проведем вспомогательную прямую АС.

Рассмотрим четырехугольник СЕАD. С=А=90°. Так как сумма противоположных углов четырехугольника СЕАD равна 180°, то около него можно описать окружность. DЕА=DСА (опираются на дугу АС).

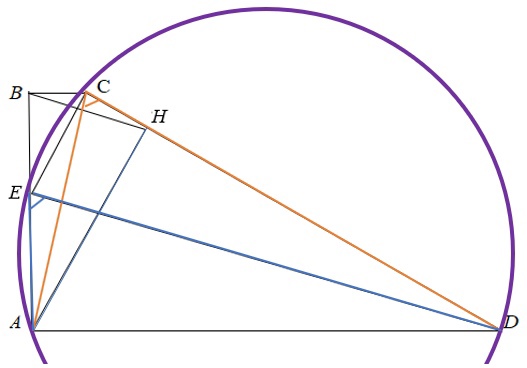
Рассмотрим четырехугольник АВСН. В=Н=90°. Так как сумма противоположных углов четырехугольника АВСН равна 180°, то около него можно описать окружность. НСА=НВА (опираются на дугу АН).

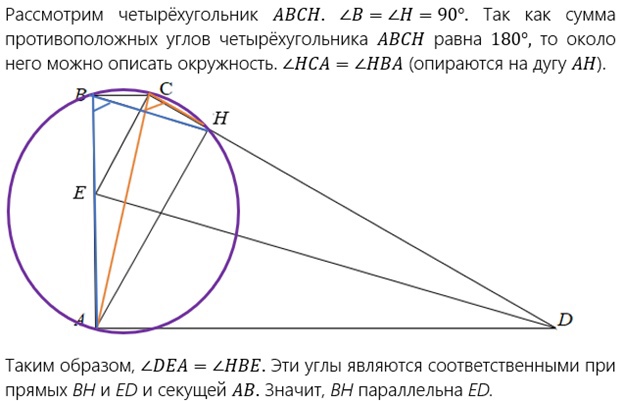
Таким образом, DЕА=НВЕ. Эти углы являются соответственными при прямых ВН и ЕD и секущей АВ. Значит, ВН параллельна ЕD.

б) Достроим трапецию АВСD до треугольника АМD продолжением боковых сторон.

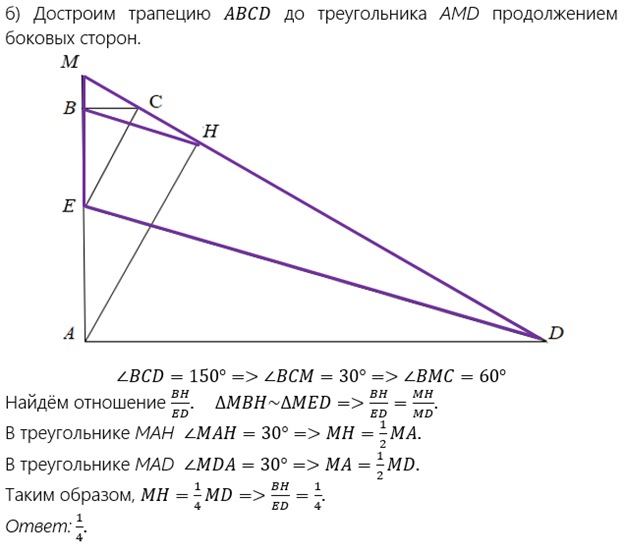
ВСD=150° = ВСМ=30° = ВМС=60°.

Найдем отношение ВН /ВD.

ΔМВН~ΔМЕD = ВН/ЕD=МН/МD.

В ΔМАН МАН=30° = МН=1/2МА.

В ΔМАD МDА=30° = МА=1/2МD.

Таким образом, МН=1/4МD = ВН/ЕD=1/4.

Ответ: ¼.