Использование различных приемов и методов
при решении дробно-рациональных уравнений
Цели: продолжить формирование умения решать дробно-рациональные уравнения, используя при этом различные приемы и методы.
Ход урока
I. Организационный момент.
II. Устная работа.
Какие из чисел –1; 0; 2; 3 являются корнями уравнения:
а) 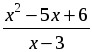 = 0; б)
= 0; б) 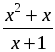 = 0.
= 0.
III. Объяснение нового материала.
1. Сначала необходимо актуализировать знания учащихся, попросив их рассказать алгоритм решения дробно-рациональных уравнений. После этого предложить учащимся использовать этот алгоритм при решении уравнения.
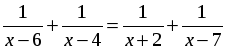 (пример 2 из учебника).
(пример 2 из учебника).
Далее делается в ы в о д, что решение данного уравнения по алгоритму является громоздким, поэтому целесообразно применить ряд преобразований.
2. Рассмотреть пример 4 из учебника. Здесь возникает такая же ситуация: решение данного дробно-рационального уравнения приводит к целому уравнению четвертой степени, корни которого известными методами найти очень сложно. Зато после введения новой переменной полученное уравнение решается довольно просто.
3. На основании рассмотренных примеров делаются следующие
в ы в о д ы:
1) Не всякое дробно-рациональное уравнение целесообразно решать по алгоритму.
2) Довольно эффективным методом решения дробно-рациональных уравнений является метод введения новой переменной.
IV. Формирование умений и навыков.
Упражнения:
1. № 293 (а), № 294 (а).
2. № 297 (а, б), № 298 (б).
В классе с высоким уровнем подготовки можно решить еще несколько дробно-рациональных уравнений.
3. № 299 (а).
Р е ш е н и е
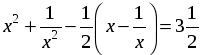 .
.
С д е л а е м з а м е н у: 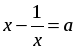 , тогда
, тогда
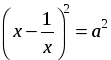
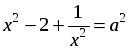
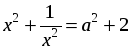
Получим уравнение:
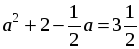 ;
;
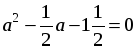 ;
;
2а2 – а – 3 = 0;
а1 = –1, а2 = 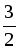 .
.
В е р н е м с я к з а м е н е:
| 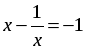 ; или ; или х2 + х – 1 = 0; D = 1 + 4 = 5; х1, 2 =  . . | 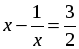 ; ;
2х2 – 3х – 2 = 0; D = 9 + 16 = 25; х1 = 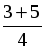 = 2; = 2; х2 = 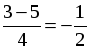 . . |
О т в е т: 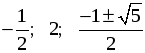 .
.
4. 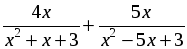 = –1,5.
= –1,5.
Р е ш е н и е
Проверим, что х ≠ 0, и разделим числитель и знаменатель каждой дроби на х:
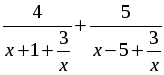 = –1,5.
= –1,5.
С д е л а е м з а м е н у: 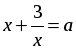 . Получим:
. Получим:
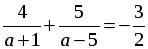 ;
;
8 (а – 5) + 10 (а + 1) + 3 (а + 1) (а – 5) = 0;
8а – 40 + 10а + 10 + 3а2 – 15а + 3а – 15 = 0;
3а2 + 6а – 45 = 0;
а2 + 2а – 15 = 0;
а1 = –5, а2 = 3.
В е р н е м с я к з а м е н е:
| 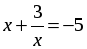 ; или ; или х2 + 5х + 3 = 0; D = 25 – 12 = 13; х1, 2 = 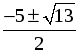 . . | 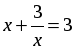 ; ;
х2 – 3х + 3 = 0; D = 9 – 12 = –3. Решений нет. |
О т в е т: 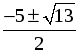 .
.
5.  = 3.
= 3.
Р е ш е н и е
Вычтем и прибавим к выражению, стоящему в левой части уравнения, выражение  , чтобы получить полный квадрат:
, чтобы получить полный квадрат:
;
;
;
.
С д е л а е м з а м е н у:  = t. Получим:
= t. Получим:
t2 + 2t – 3 = 0;
t1 = 1, t2 = –3.
В е р н е м с я к з а м е н е:
|  = 1; или = 1; или х2 – х – 1 = 0; D = 1 + 4 = 5; х1, 2 =  . . |  = –3; = –3;
х2 + 3х + 3 = 0; D = 9 – 12 = –3. Решений нет. |
О т в е т:  .
.
V. Проверочная работа.
В а р и а н т 1
Решите уравнение:
а) ;
б) .
В а р и а н т 2
Решите уравнение:
а) ;
б) .
VI. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какими приемами и методами можно решать дробно-рациональные уравнения?
– Опишите решение дробно-рационального уравнения по алгоритму.
– В каких случаях при решении дробно-рациональных уравнений целесообразно использовать метод введения новой переменной?
Домашнее задание: № 296 (б), № 294 (б), № 297 (в), № 298 (б).
Д о п о л н и т е л ь н о: № 299 (б).
У р о к 7 (30).
Алгоритм решения неравенств
второй степени с одной переменной
Цели: ввести понятие неравенства второй степени с одной переменной и изучить алгоритм решения таких неравенств.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Определите количество корней уравнения ах2 + bx + c = 0 и знак коэффициента а, если на рисунке изображен график функции у = ах2 +
+ bx + c.
а) б)
в)
2. Назовите промежутки знакопостоянства функции у = ах2 + bx + c, если ее график изображен на рисунке:
а) б)
в)
III. Объяснение нового материала.
1. В в е д е н и е п о н я т и я неравенства второй степени с одной переменной.
З а д а н и е. Какие из следующих неравенств являются неравенствами второй степени с одной переменной?
а) 2х2 + 3х – 1 0; г) 2х2 – х + 1 х4;
б) 4х2 – х ≤ 0; д)  х2 ≥ 1;
х2 ≥ 1;
в) 5х – 1 3х2; е) х2 – 4x .
2. С о с т а в л е н и е а л г о р и т м а решения неравенств второй степени с одной переменной.
Поставить перед учащимися проблему: как может быть решено неравенство подобного вида? Если учащиеся не догадаются, то можно вернуться к заданиям устной работы и наводящими вопросами помочь им сделать в ы в о д: неравенства второй степени с одной переменной решаются графически.
Желательно, чтобы учащиеся самостоятельно вывели алгоритм решения этих неравенств.
3. Р а с с м о т р е н и е п р и м е р о в решения неравенств второй степени с одной переменной.
IV. Формирование умений и навыков.
На этом уроке необходимо рассмотреть разные ситуации, возникающие при решении неравенств второй степени с одной переменной. Нужно, чтобы учащиеся запомнили алгоритм и применяли его без помощи учителя.
В соответствии с количеством корней трехчлена, получаемых в процессе решения неравенств, все задания можно разбить на три группы. В первую группу войдут неравенства, у которых квадратный трехчлен имеет два корня, во вторую – один корень, и в третьей группе будут неравенства, квадратный трехчлен которых не имеет корней.
Упражнения:
1-я г р у п п а.
№ 304 (а, в, ж), № 308 (а, в, д).
2-я г р у п п а.
1. № 304 (д).
2. 9х2 + 6х + 1 ≤ 0
3-я г р у п п а.
а) х2 + 2х + 4 0;
б) 2х2 – х + 3 ≤ 0;
в) –х2 + 3х – 7
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какие неравенства называются неравенствами второй степени с одной переменной?
– Опишите алгоритм решения неравенств второй степени с одной переменной.
– Какие решения может иметь неравенство второй степени с одной переменной, если соответствующий квадратный трехчлен не имеет корней?
Домашнее задание: № 304 (б, г, е, з), № 306 (б, в), № 308 (б, г).







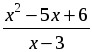 = 0; б)
= 0; б) 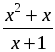 = 0.
= 0.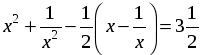 .
.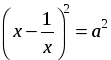
 .
.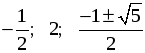 .
.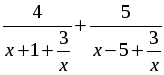 = –1,5.
= –1,5.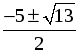 .
.


















