Обобщение опыта работы
Бостановой Светланы Умаровны
учителя математики и информатики
МКОУ СШ №2 г.Теберда имени М. И. Халилова
по теме: « Использование современных образовательных технологий на уроках математики»
Модернизация образования требует сегодня от учителя коренного улучшения учебно-воспитательного процесса. Последние годы сильно снизился интерес учащихся к предметам физико-математического цикла. Математика – царица наук перестала привлекать ребят красотой чертежей, формул, логической строгостью доказательств. Они не хотят посещать математические кружки, факультативы, практикумы по решению нестандартных задач.
Познакомившись с модулем «Современные педагогические технологии», я заинтересовалась технологиями дифференцированного обучения. Считаю, что каждому ребенку для развития и саморазвития нужна образовательная среда, включающая:
организацию и использование учебного материала разного содержания, вида и форм;
представление ученику свободы выбора способов выполнения учебных заданий (при снятии эмоционального напряжения в связи с боязнью ошибиться в своих действиях);
использование нетрадиционных форм, групповых и индивидуальных занятий в целях активизации творчества детей;
создание условий для творчеств в самостоятельной и коллективной деятельности;
постоянное внимание педагога к анализу и оценке индивидуальных способов учебной работы, побуждающих ученика к осознанию им не только результата, но и процесса самой работы;
разработку и использование индивидуальных программ обучения, моделирующих исследовательское (поисковое) мышление.
Моя главная задача, как учителя, обеспечивать условия для оптимального удовлетворения запросов учащихся и помогать становлению личности.
В основе дифференцированного подхода в обучении лежит внимание к каждому ученику, его творческой индивидуальности, самобытности в условиях классно-урочной системы обучения по образовательным программам. Предполагает сочетание фронтальных, групповых и индивидуальных занятий для повышения качества обучения и развития каждого школьника. Дифференцированный подход в обучении способствует более прочному и глубокому усвоению знаний, развитию индивидуальных способностей, развитию самостоятельного творческого мышления, созданию условий для возможности роста уровня приобретаемых знаний для каждого ученика.
На протяжении нескольких лет я работаю над проблемой «Дифференцированного подход в обучении на уроках математики».
Дифференциация и индивидуализация образовательного процесса не есть самоцель, а выступает лишь средством его гуманизации, ориентации на личность учащихся, более полный учет их интересов, склонностей, способностей, жизненных планов, особенно связанных с продолжением образования.
Школа, учитель теперь во многом самостоятельно вправе решать вопрос о том, чему и как учить. Быстрыми темпами идет процесс преобразования школ в дифференцированные самоуправляемые учебные учреждения самых разнообразных профилей. В связи с этим со всей остротой встает вопрос о том, чему и как учить математике в школах и классах разных профилей. Для определения стратегии дифференциации обучения предлагают условно разделить всех учащихся на три группы по отношению к курсу математики.
I группу составляют школьники, для которых математика является лишь элементом общего развития и в дальнейшей профессиональной деятельности будет использоваться лишь в незначительном объеме (учащиеся с минимальным уровнем знаний и умений). Для этой категории учащихся важно овладение общей математической культурой, а вовсе не ремесленными навыками решения каких-то стандартных задач.
Во II группу могут входить учащиеся, для которых математика будет важным инструментом в их профессиональной деятельности (учащиеся с хорошим уровнем умений и знаний). Для этой категории существенны не только знания о математических фактах, навыки логического мышления, пространственные представления, но и прочие навыки решения задач.
В III группу следует отнести тех учащихся, которые выберут математику (или близкие к ней области знаний) в качестве основы своей будущей профессии. Учащиеся этой группы проявляют повышенный интерес к изучению математики и должны творчески овладеть ее основами. Период разделения класса по уровням приходится на VII класс. Два предыдущих года обучения в средней школе учащиеся подвергаются наблюдению и диагностике. Для получения большей информации о каждом ребенке учитель предлагает всем учащимся заполнить разного рода анкеты. Одна из них приводится ниже.
Анкета
1. Класс.
2. Фамилия, имя.
3. Где и кем работают родители?
4. Отношение родителей к математике? (Имеют математическое образование; применяют математику в своей работе; увлечены математикой, не любят математику, совсем не интересуются ею). Подчеркнуть нужное.
5. Есть ли в домашней библиотеке математические книги, но не учебники по математике для средней школы? (Да, нет). Подчеркнуть нужное.
6. Кто больше всего помогает готовить уроки по математике?
7. Сколько времени занимает подготовка к математике?
8. Почему ты учишь математику? (Желательно ответить откровенно и полно.)
9. Хочешь ли ты знать больше, чем дают на уроке? (Да, нет.) Подчеркнуть нужное.
10. Как дается тебе математика? (Легко, много надо заучивать, трудно). Подчеркнуть нужное.
11. Твое отношение к математике? (Люблю; учу, чтобы получить хорошую оценку; чтобы не ругали дома; скучно на уроках; не хочу ее учить). Подчеркнуть нужное.
12. Какими знаниями по математике ты владел до прихода в школу? (Счет до 10 и обратно; сложение в пределах десятка; решение простых задач.) Подчеркнуть нужное.
13. Какого вида задания по математике тебе нравятся больше? (Задачи, примеры, задачи и примеры). Подчеркнуть нужное.
14. Мечтаешь ли ты связать свою жизнь с математикой? (Буду математиком; хочу поступить в вуз, где нужно будет сдавать математику; хочу знать как можно больше о разном, не только о математике.) Подчеркнуть нужное.
О том, в какую группу попал данный ученик, обязательно сообщалось его родителям. Беседа с родителями проходит в доброжелательном тоне. И родители, и учащиеся должны будут понять, что состав группы не закреплен раз и навсегда. Впоследствии можно перейти из одной группы в другую в соответствии с результатами обучения и желанием учащегося. Период неустойчивого состояния групп продолжается в VIII—IX классах.
Требования к уровню математической подготовки можно определить следующим образом. Учащиеся, овладевающие курсом на общекультурном уровне, должны хорошо понимать учебный материал, уметь его разъяснять и применять в бытовой сфере. Учащиеся, овладевающие материалом на прикладном уровне, должны помимо этого овладеть системой умений и навыков по применению знаний в самых разных областях, особенно в тех, которые связаны с выбранной профессией.
На творческом уровне учащимся предъявляются дополнительные требования в смысле доказательности математических фактов, у них должна быть выработана внутренняя потребность проведения достаточного строгих математических доказательств.
Таким образом, общее требование ко всем трем группам – глубокое понимание учебного материала и умение его разъяснить.
Расскажу, как я провожу дифференциацию на уроках математики в течение уже многих лет. И эта система дает результаты. В своей работе идею дифференциации обучения использую почти на каждом уроке.
В 5-9 классах учащихся условно делаю на варианты А и Б. Задания варианта А соответствуют обязательному уровню математической подготовки, варианта Б – более сложные.
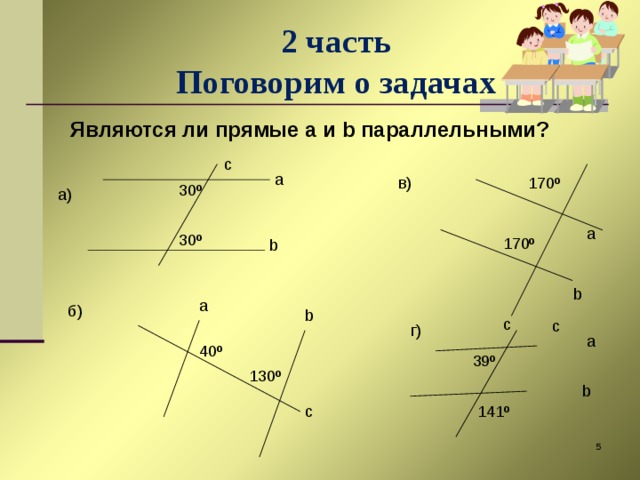
Сейчас расскажу, как дифференциация прослеживается на различных этапах урока.
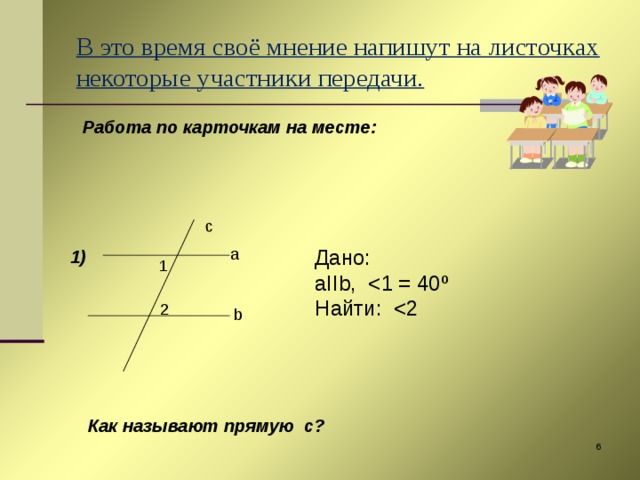
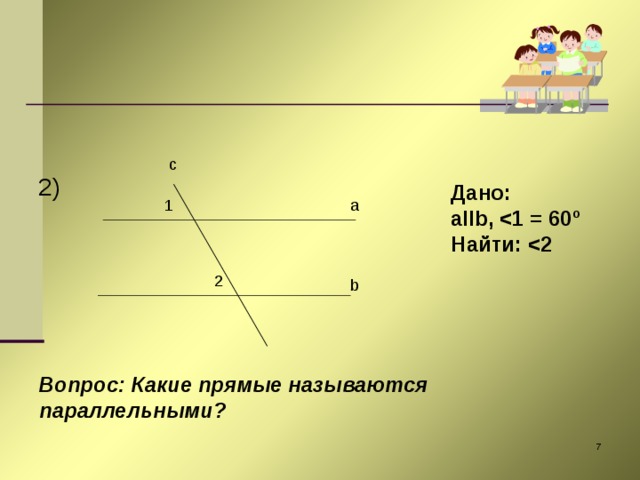
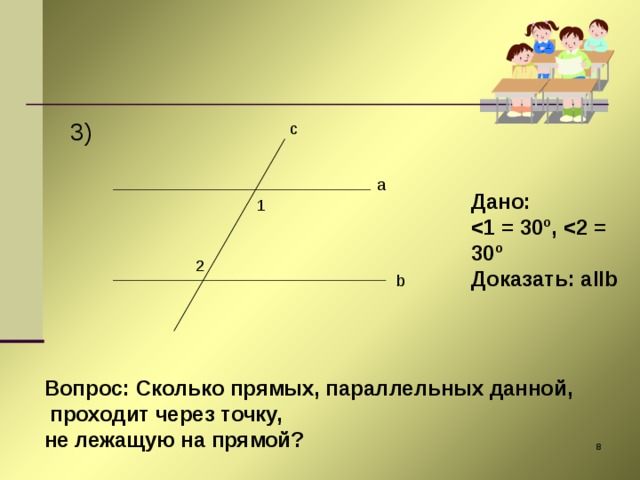
1) В начале урока на устном счете, на устных упражнениях, задания на доске пишу и для учащихся варианта А и Б, тем самым проверяя знания правил, теорем, свойств всеми учащимися и умением применить эти правила к конкретной задаче. Особенно это проявляется на уроках геометрии, так как этот предмет вызывает особые трудности. На доске заготавливаю чертежи к задачам и одношаговым, где надо сразу применить изученную теорему или свойства данной фигуры, и многошаговым задачам, комбинированным, чтобы проследить ход мыслей учащихся, их логическое мышление, заставить найти план решения, исходя из данных. Эти задачи для учащихся варианта Б.
2) При закреплении материала задания подбираю таким образом, чтобы сначала усвоение шло на более легких примерах, затем учащимся варианта Б даю усложненные задания , предварительно обсудив их. Ученики решают эти задания самостоятельно, а с учащимися варианта А продолжаем закреплять материал на основных заданиях. Правильность решения заданий варианта Б проверяю по ходу урока, подходя к учащимся на месте. Работу таким образом проводить трудно, но стараюсь не упускать из виду учащихся, которые материал усваивают быстро и пополнять запас их знаний более сложными заданиями. Так работаю во всех классах.
3) К урокам составляю дифференцированные карточки, с учетом возможностей учащихся. Это и перфокарты, и карточки многоразового использования, и математическое лото.
4) Дифференцированно провожу и контроль усвоения материала. Контрольные и самостоятельные работы составляю разноуровневые на три варианта. Вариант III рассчитываю на слабо подготовленных учащихся. Главная задача – проверить степень усвоения обязательного уровня математической подготовки, определенного стандартом образования. Вариант I и II усложняю: наряду с заданиями, направленными на проверку основных умений, в них содержатся задания, требующие логического мышления, комбинированные задачи и задания на сообразительность и внимание. Иногда, в зависимости от конкретного материала, провожу контрольные работы по-другому. В I и II вариантах даю пять заданий. Первые три – на проверку обязательного уровня – на оценку «3», четвертое задание, требующее дополнительных знаний – на «4», пятое задание, требующее не только свободного владения приобретенными знаниями и умениями, но и творческого подхода – на оценку «5». Такие задания включаю в каждую контрольную работу. Это дает возможность правильно оценить знания учащихся, судить об их возможностях, сформированных умениях и навыках, способов деятельности.
5) Дифференцированно подхожу и к домашнему заданию: учащимся даю задания для варианта А – самые простые, для в. Б – сложнее.
Итак, работая дифференцированно с учащимися, вижу, что их внимание не падает на уроке, так как каждому есть посильное задание, «сильные» ученики не скучают, так как всегда им дается задача, над которой надо думать. Ребята постоянно заняты посильным трудом.
Применение дифференциации при обучении математике, как одного из путей учета индивидуальных особенностей учащихся, необходимо и возможно.
Дифференциация способствует более прочному и глубокому усвоению знаний, развитию индивидуальных способностей, развитию самостоятельного творческого мышления. Разноуровневые задания облегчают организацию занятия в классе, создают условия для продвижения школьников в учебе в соответствии с их возможностями.
Слабые учащиеся охотно выполняют задания, содержащие инструктивный материал, особенно те упражнения, в которых приведены данные для самоконтроля. Это позволило сделать вывод, что таким школьникам недостаточно только показать ответ (как это делается в учебнике). Выяснив, что получен неверный ответ к заданию, ученик не в состоянии проследить всю цепочку и найти ошибку.
Предлагая задания творческого характера, нельзя рассчитывать, что учащиеся, тем более слабые, смогут самостоятельно их выполнить. Однако результаты показывают, что творческие задания стимулируют познавательную активность слабых школьников. Ребята, потратившие определенные усилия на творческие задания, охотно принимают участие в обсуждении этих заданий, с интересом выслушивают объяснения приемов их решения даже в тех случаях, когда они этих приемов сами найти не смогли.
Разноуровневые задания, составленные с учетом возможностей учащихся, создают в классе благоприятный психологический климат. У ребят возникает чувство удовлетворения после каждого верно решенного задания. Успех, испытанный в результате преодоления трудностей, даёт мощный импульс повышению познавательной активности. У учащихся, в том числе и у слабых, появлялась уверенность в своих силах, они уже не чувствуют страха перед новыми задачами, рисковать пробовать свои силы в незнакомой ситуации, берутся за решение задач более высокого уровня. Все это способствует активизации мыслительной деятельности учащихся, созданию положительной мотивации к учению.
Приложение 1
Приложение 2
Презентация 1
Презентация 2
При подготовке к ГИА эти уроки наиболее эффективны, так как позволяют учителю видеть, на каком уровне работает каждый ученик, позволяют повысить уровень обученности учащихся.
Технология применяется и в домашней работе. Я составляю дифференцируемые домашние задания , контрольные работы, зачеты по геометрии тоже содержат разноуровневые задания.
Контроль позволяет мне не только правильно оценить уровень усвоения учащимися изучаемого материала, но и увидеть свои собственные удачи и промахи, внести необходимые коррективы и в свою работу и в работу учащихся. Для проверки знаний, умений и навыков использую различного рода тесты:
на заполнение пропусков в истинных утверждениях или верно сформулированных определениях;
на установление истинности (ложности) предложенного утверждения;
на выбор правильного ответа.
По сравнению с другими видами контроля (зачет, самостоятельная или контрольная работа) тест позволяет при минимальных затратах времени проверить усвоение значительного по объему учебного материала.
Однако нельзя считать тестирование - основной формой контроля знаний учащихся. Так как распространение тестов как основной формы проверки в математике неизбежно приведет к вытеснению из процесса обучения соответствующей деятельности, формирующей и развивающей мышление растущего человека (школьника).
Открытость требований приводит к тому, что у учащихся появляется заинтересованность в получении знаний. Причем введенное уровнем обязательной подготовки «ограничение снизу» повышает и последующие более высокие уровни. «Четверки» и «пятерки» стали более полновесными. Ученик сам выбирает для себя уровень ответа и заинтересован прийти к зачету (или контрольной работе) с определенным багажом, позволяющим ему сдать его на должном (им самим определенном) уровне. Учащиеся учатся планировать свою деятельность, видеть конечные цели своей работы, распределять свои силы на достаточно долгий промежуток времени, добиваться поставленной цели.
Применяемые на уроках
дифференцированные задания ;
тренинговые задания;
задачи по готовым чертежам .
электронные образовательные ресурсы и т.д.
позволяют мне стимулировать творческий поиск учащихся; воспитывать самостоятельность и ответственность за результаты учебы и поступки; реализовать принципы: щадящей педагогики, равных условий, гласности и др. Организация учебно-воспитательного процесса на основе педагогики сотрудничества, умение создать благоприятный морально-психологический климат в детском коллективе, обладание психолого-педагогическим тактом привели к увеличению процента учащихся, испытывающих интерес к изучению математики.
На сегодняшний день информационно – коммуникационные технологии занимают всё большее и большее место в образовательном процессе. Главным преимуществом этих технологий является наглядность, так как большая доля информации усваивается с помощью зрительной памяти, и воздействие на неё очень важно в обучении. Применение информационных технологий в работе помогают мне сделать процесс обучения творческим и ориентированным на учащегося.
ИКТ использую на уроках, применяя образовательные и обучающие программы, создаю к урокам презентации, использую мультимедийное оборудование для показа видео по различным темам разделов курса математики.
Использование ИКТ на уроках математики мне позволяет: сделать процесс обучения более интересным, ярким, увлекательным за счёт богатства мультимедийных возможностей; эффективно решать проблему наглядности обучения; расширить возможности визуализации учебного материала, делая его более понятным и доступным для учащихся, индивидуализировать процесс обучения за счёт возможности создания и использования разноуровневых заданий.
Замечено, что учащиеся проявляют большой интерес к теме, когда при объяснении нового материала применяются презентации. Даже пассивные учащиеся с огромным желанием включаются в работу.
Использую ИКТ на разных этапах урока:
Устный счёт включает в себя устные упражнения, необходимые либо для закрепления, либо для дальнейшего изучения нового материала;
На этапе первичного закрепления. Предложенные учителем задания по новой теме, позволяют определить степень усвоения нового материала;
При проверке домашнего задания. Предлагаю выполнить домашнюю работу или её часть в форме презентации (По желанию ученика) .
При объяснении нового материала;
При закреплении, повторении используются готовые демонстрационные – энциклопедические программы из серии: "Виртуальная школа Кирилла и Мефодия” .
На этапе контроля ЗУН.
Использую ИКТ и на уроках решения тренировочных заданий при подготовке к ГИА.
Уроки- презентации играют важную роль. Они реализуют принципы доступности, наглядности. Они эффективны своей эстетической привлекательностью; между учителем и учеников существует посредник- компьютер, что способствует эффективному взаимодействию. Урок – презентация так же обеспечивает большой объем информации и заданий за короткий период. К тому же всегда можно вернуться к предыдущему слайду. Обычная школьная доска не вмещает всю нужную для урока информацию. Слайд такую возможность реализует.
Использование информационных технологий в образовательном процессе делает обучение более содержательным, наглядным, разнообразным, способствует развитию самостоятельности и творческих способностей обучаемого, существенно повышает уровень индивидуализации обучения.
Задания на тестовой основе получили широкое распространение в практике преподавания. Тестовые технологии я использую на различных этапах урока, при проведении занятий разных типов, в ходе индивидуальной, групповой и фронтальной работы, в сочетании с другими средствами и приемами обучения. Часто тестовые задания использую при проведении зачетов по геометрии, алгебре в 5- 9 классах. Сегодня существуют разнообразные варианты тестов. Тематические тесты очень удобно проводить после изучения всей темы. В результате тестирования можно увидеть, на сколько качественно, полно, осознанно ученик овладел материалом.
Тестовая технология помогает при контроле знаний учащихся. Тест обеспечивает субъективный фактор при проверке результатов, а так же развивает у ребят логическое мышление и внимательность.
Тестовые задания различаются по уровню сложности и по форме вариантов ответов. Использование тестовых заданий позволяет осуществить дифференциацию и индивидуализацию обучения учащихся с учетом их уровня познавательных способностей.
Моя задача, как учителя, организовать учебную деятельность таким образом, чтобы полученные знания на уроке учащимися были результатом их собственных поисков. Но эти поиски необходимо организовать, при этом управлять учащимися, развивать их познавательную активность.
Неоспорим тот факт, что весь процесс образования и воспитания должен строиться и на принципах здоровьесбережения. Сохранять и укреплять здоровье учащихся мне помогают здоровьесберегающие технологии. Как учитель, я должна на уроках создать условия для сохранения здоровья, сформировать у ученика необходимые знания и навыки по здоровому образу жизни, научить использовать полученные знания в повседневной жизни. Поэтому: на уроках соблюдаю требования САНПиНа; создаю обстановку доброжелательности, положительного эмоционального настроя, ситуации успеха и эмоциональные разрядки, т.к. результат любого труда, а особенно умственного, зависит от настроения, от психологического климата – в недоброжелательной обстановке утомление наступает быстрее;
чёткая организация учебного труда для предупреждения утомляемости; при планировании урока предусматриваю смену деятельности, чередую различные виды активности: интеллектуальная – эмоциональная– двигательная.
Системная работа по использованию мною современных педагогических технологий и их элементов в образовательном процессе приводит к тому, что успеваемость по математике составляет 100%, учащиеся принимают активное участие в предметных неделях, участвуют в олимпиадах, у слабых учащихся снижается порог тревожности, повышается познавательный интерес к предмету.







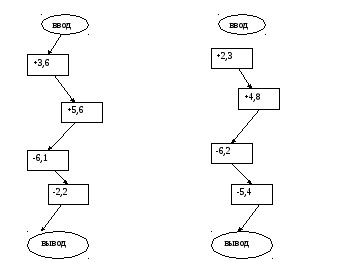
 I
I