Исследование функций а монотонность и экстремумы

Методические рекомендации по

исследованию функций на монотонность и экстремумы

Для исследования функции на монотонность и экстремумы необходимо уметь:

1. Вычислять производные функций;

2. Решать линейные и квадратные уравнения.

Знать:

1. Необходимый и достаточный признаки монотонности;

2. Необходимый и достаточный признаки экстремума.

Таблица производных функции f(x):

Необходимый и достаточный признаки монотонности: Если 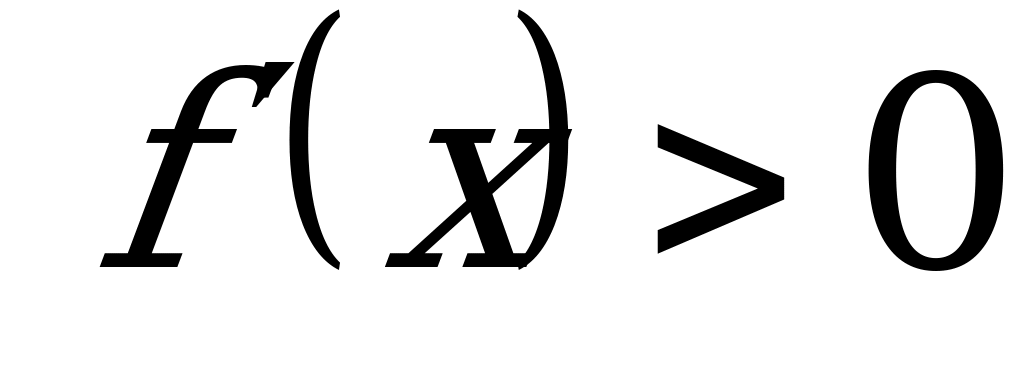на отрезке 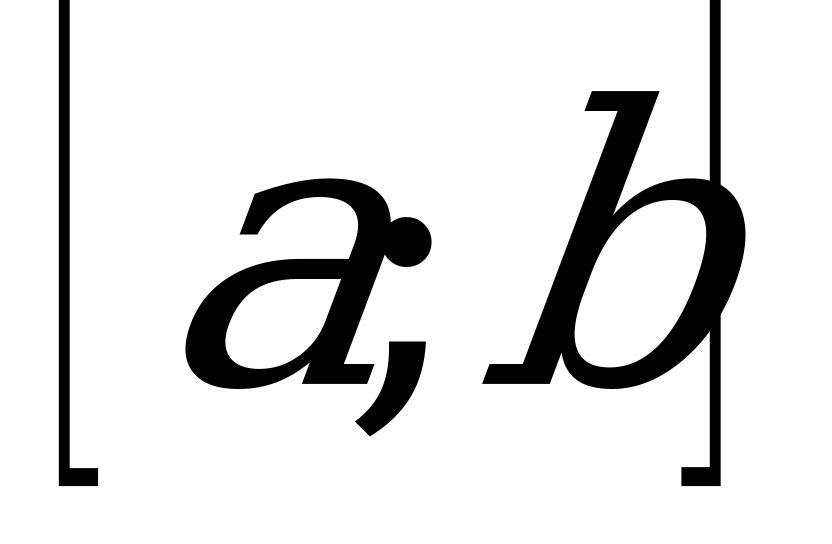, то функция 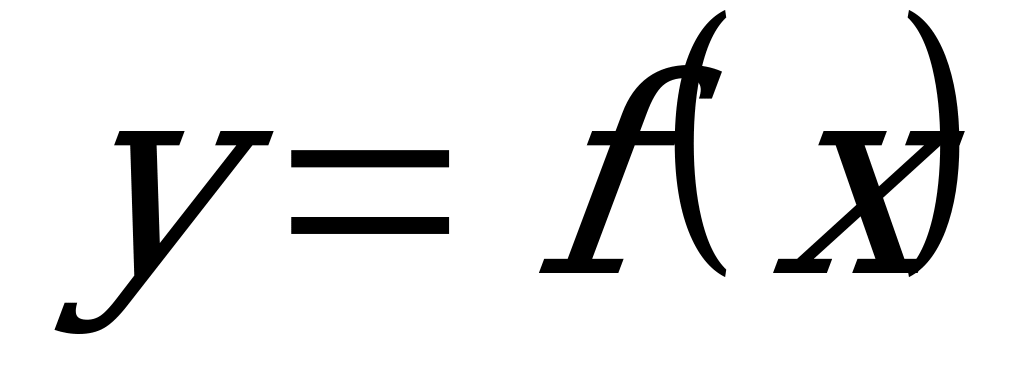возрастает на этом отрезке. Если 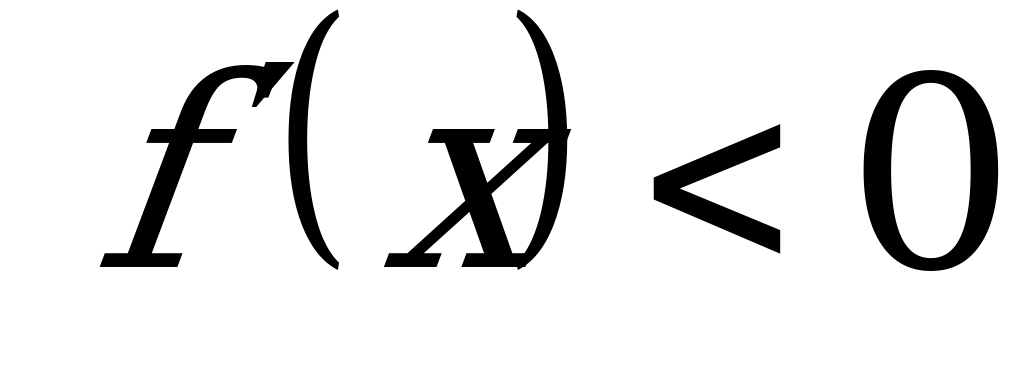на отрезке 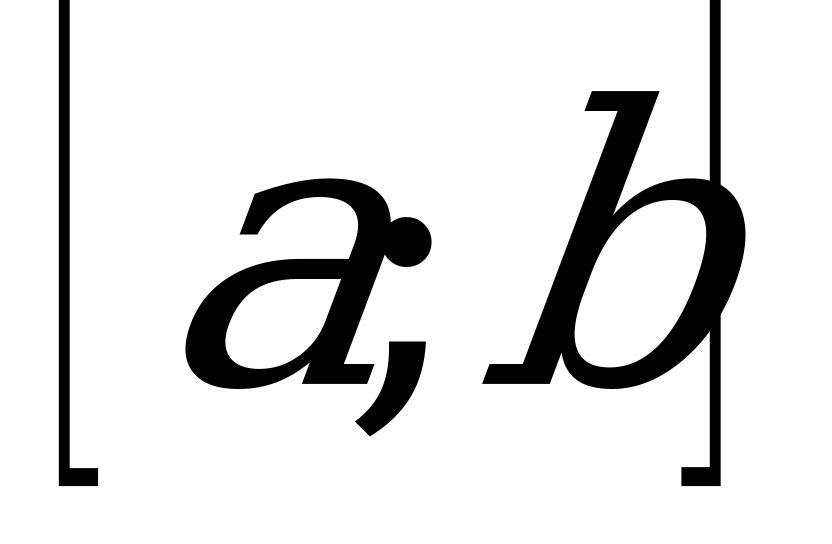, то функция 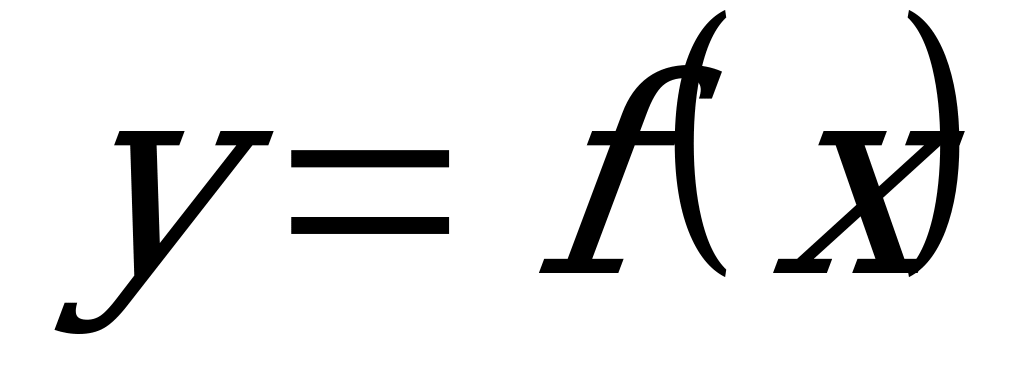убывает на этом отрезке.

Признак максимума функции: Если функция 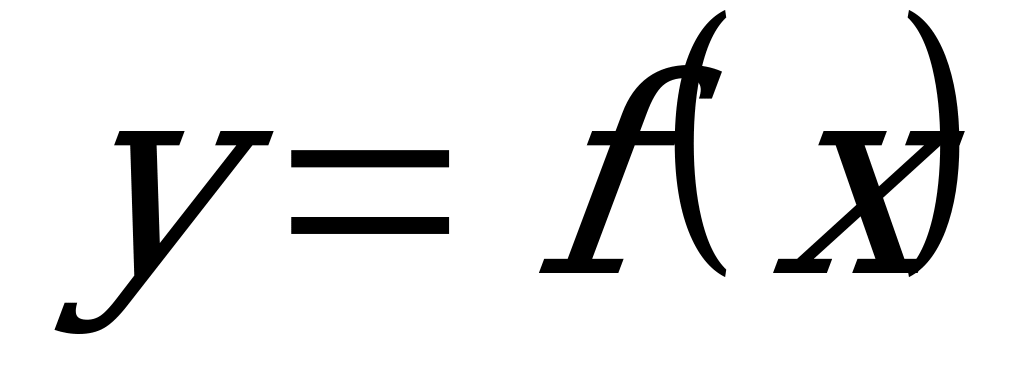непрерывна в точке 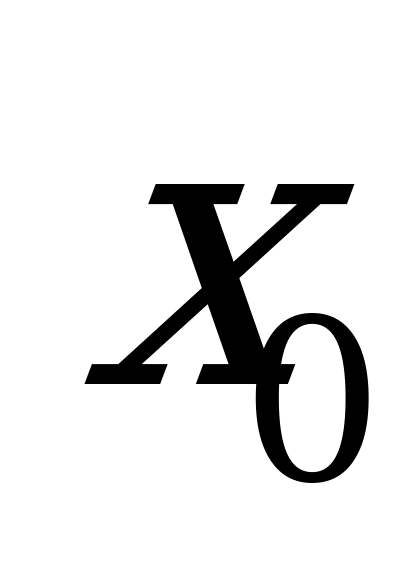, а ее производная при переходе через эту точку слева направо меняет знак с "+" на "-", то точка 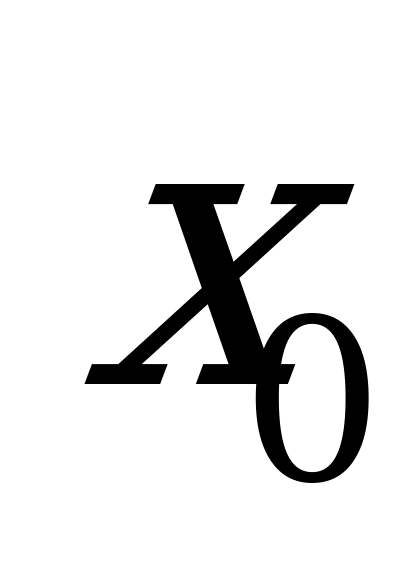является точкой максимума функции .

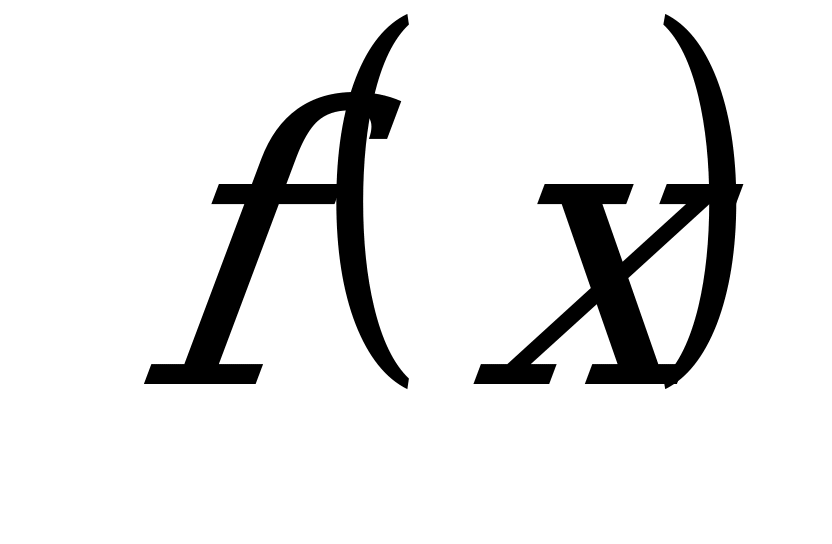Признак минимума функции: Если функция 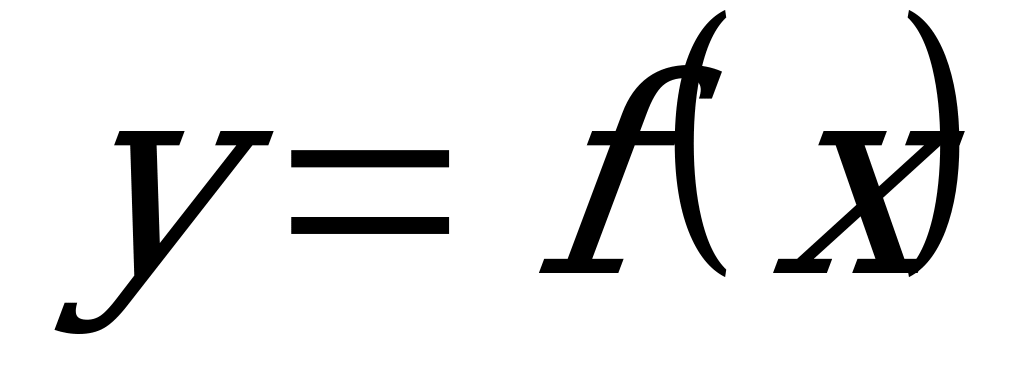непрерывна в точке 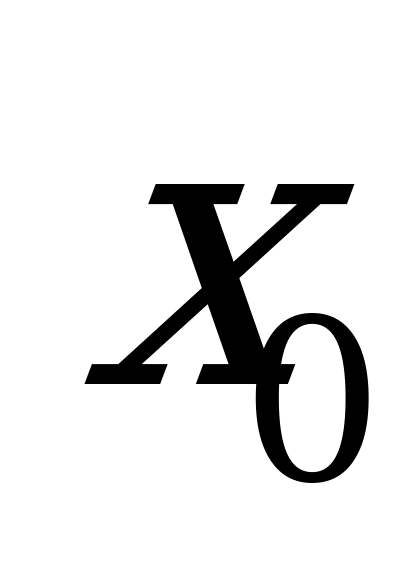, а ее производная при переходе через эту точку слева направо меняет знак с "-" на "+", то точка 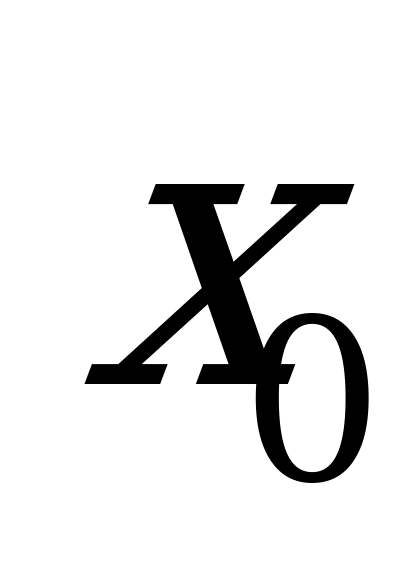является точкой минимума функции .

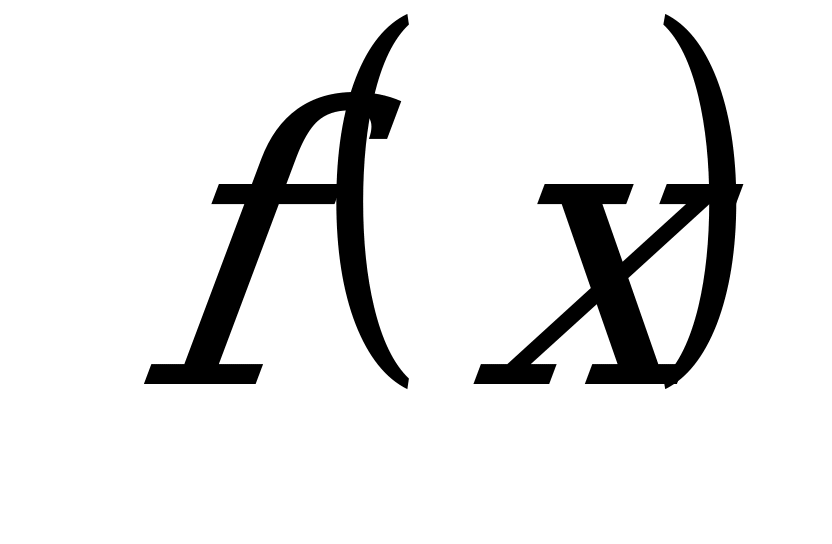Алгоритм исследования функции на монотонность и экстремумы:

1) Найти область функции.

2) Вычислить производную заданной функции .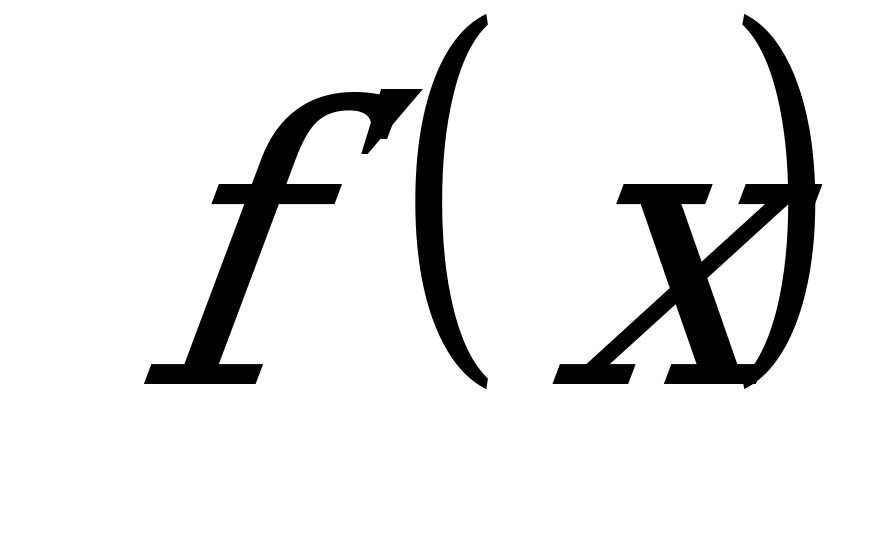

3) Найти критические точки, т. е. решить уравнение .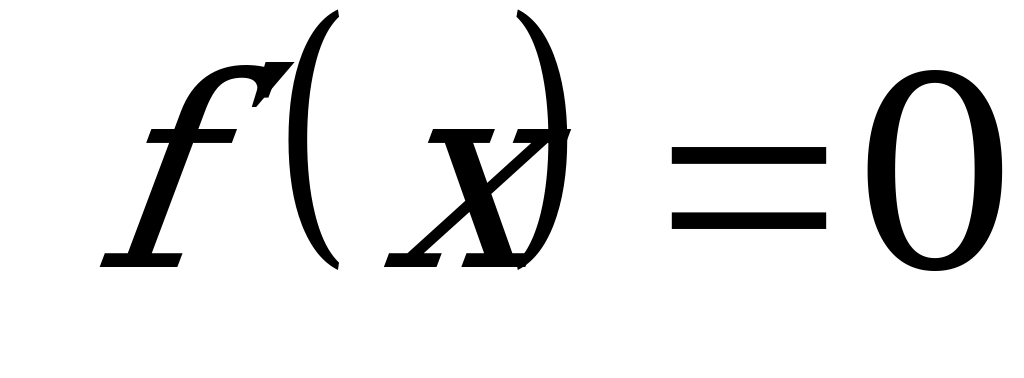

4) Исследовать знак производной в окрестности критических точек.

5) Используя необходимый и достаточный признаки монотонности и экстремумов, определить промежутки возрастания и убывания функции; точки максимумов и минимумов.

Пример 1. Определите промежутки монотонности функции .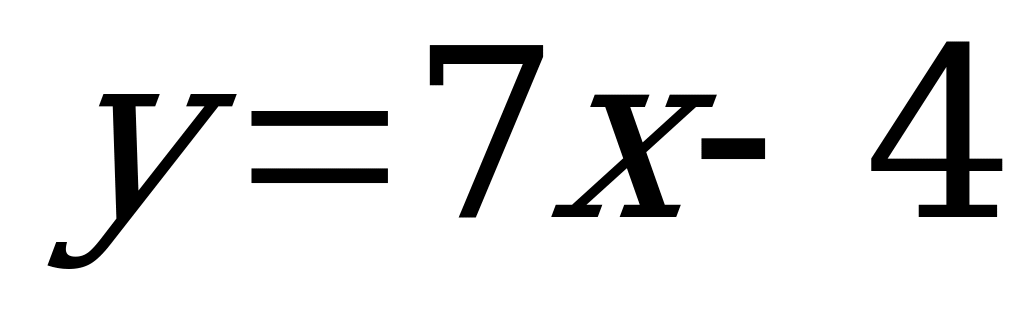

Решение:

1) Найдем область определения функции: .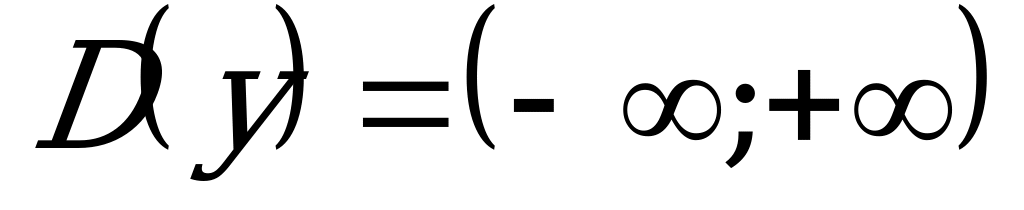

2) Вычислим производную функции: .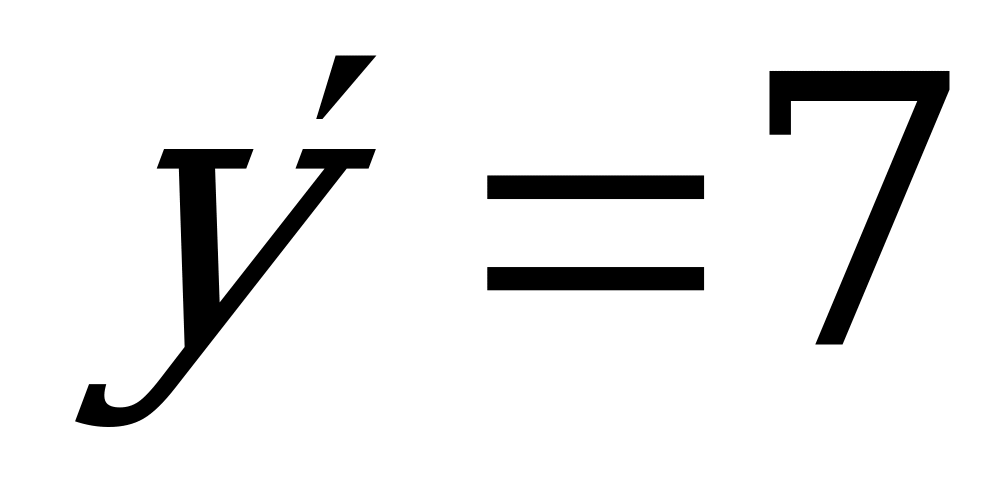

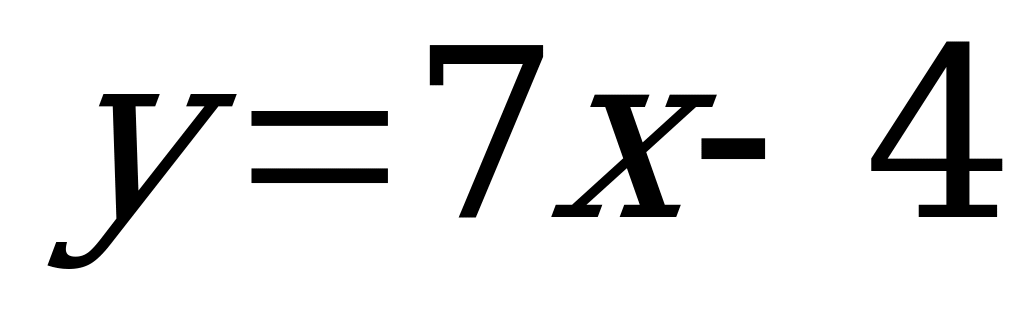Так как производная функции 0, то функция возрастает при любых значениях х.

Ответ: функция возрастает при х .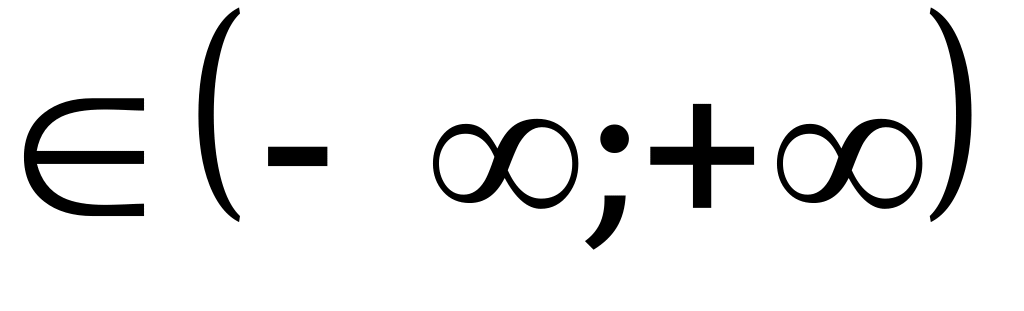

Пример 2. Дана функция 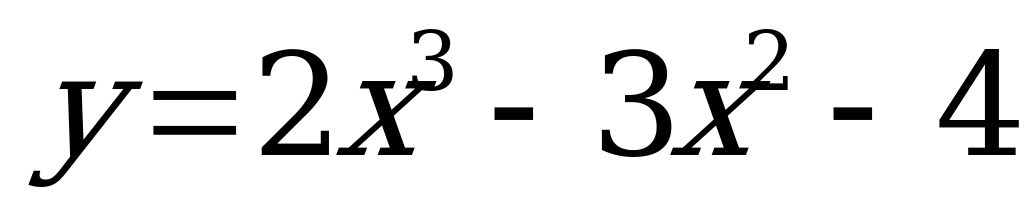. Найти:

а) промежутки возрастания и убывания;

б) точки экстремума;

Решение:

1) Найдем область определения функции: .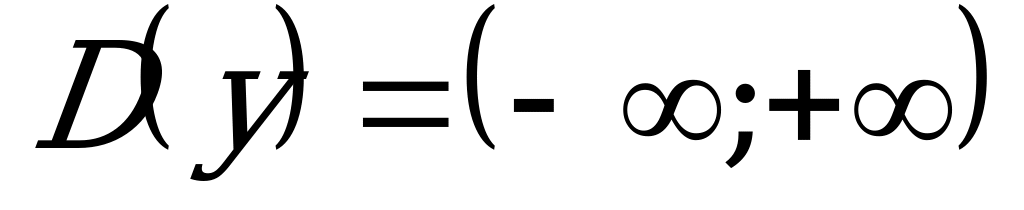

2) Вычислим производную функции: .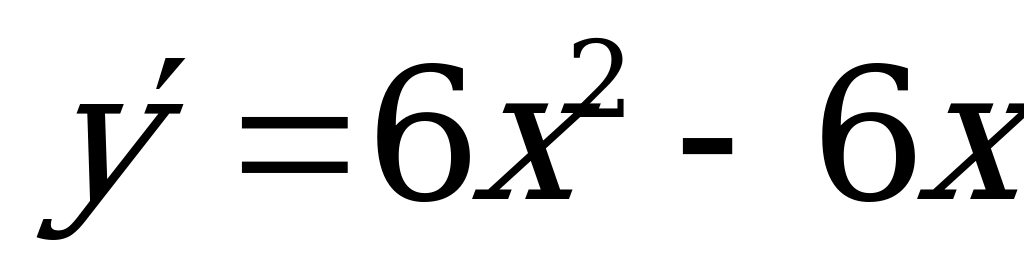

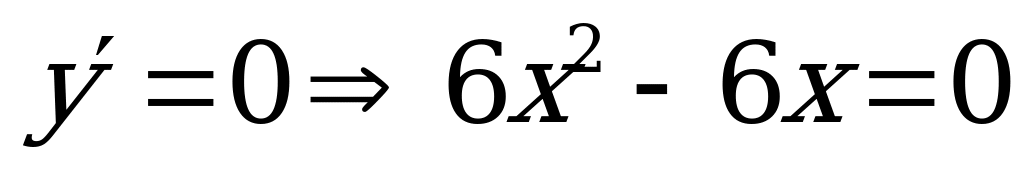
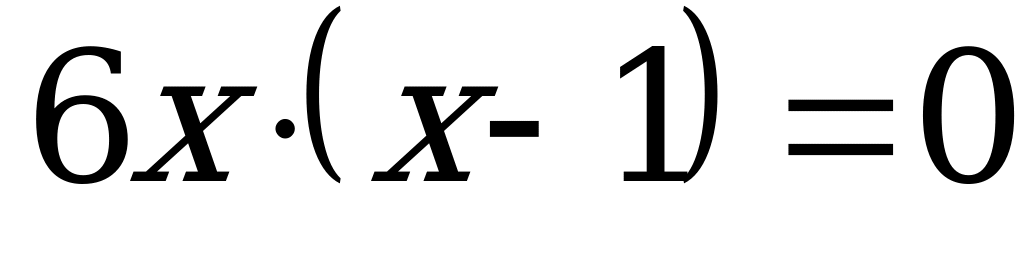
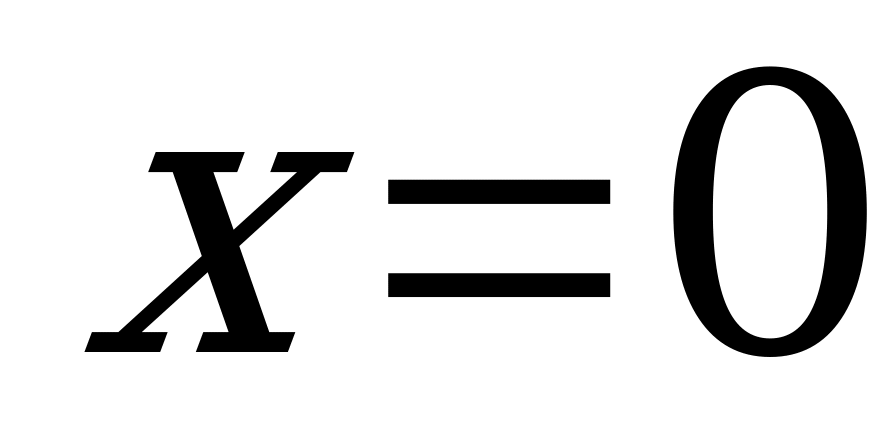3) Найдем критические точки функции:

или 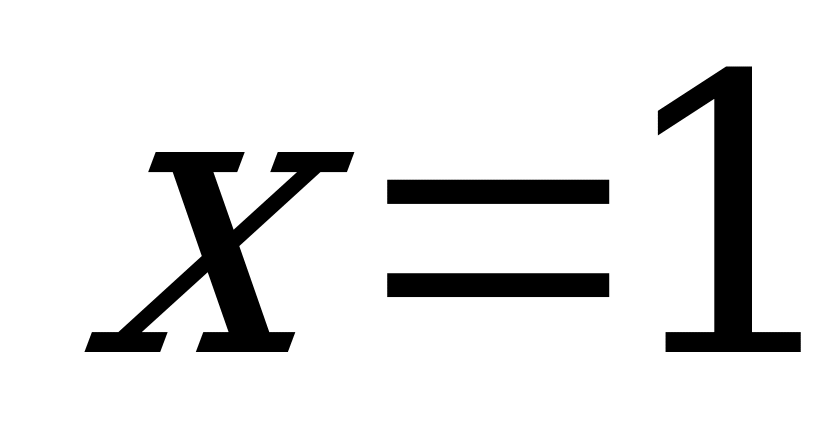- критические точки функции.

а) Исследуем знак производной в окрестностях критических точек:

Значит, функция убывает при х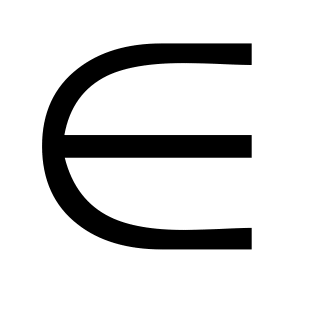 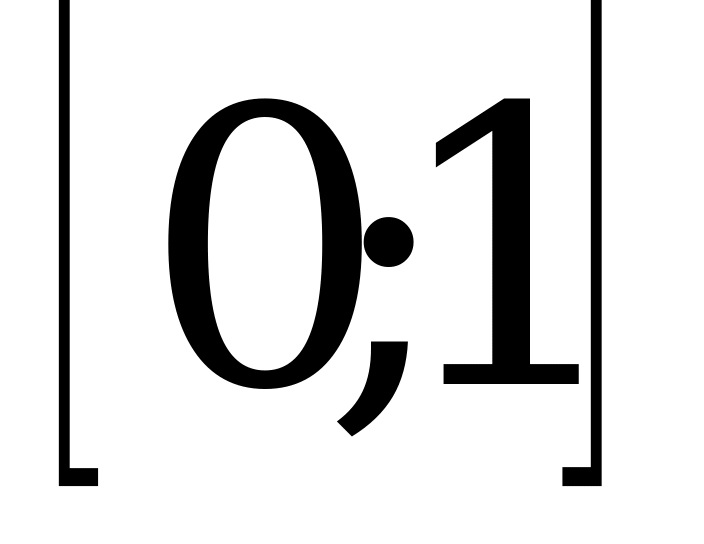,т.к. 0;

функция возрастает при х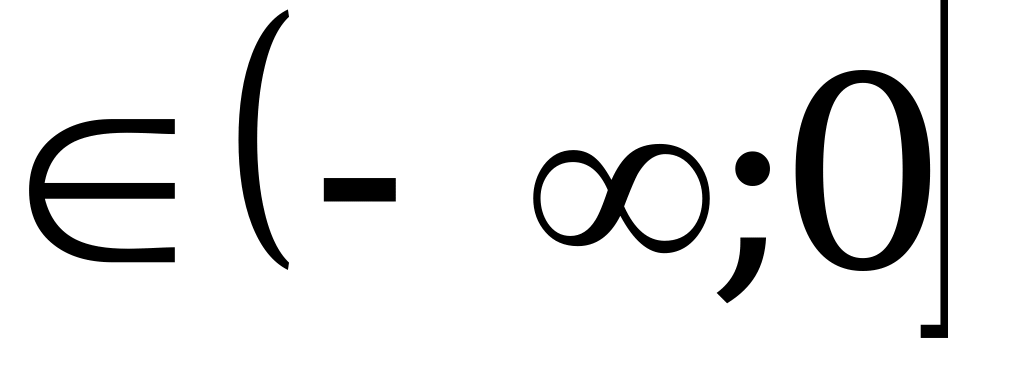 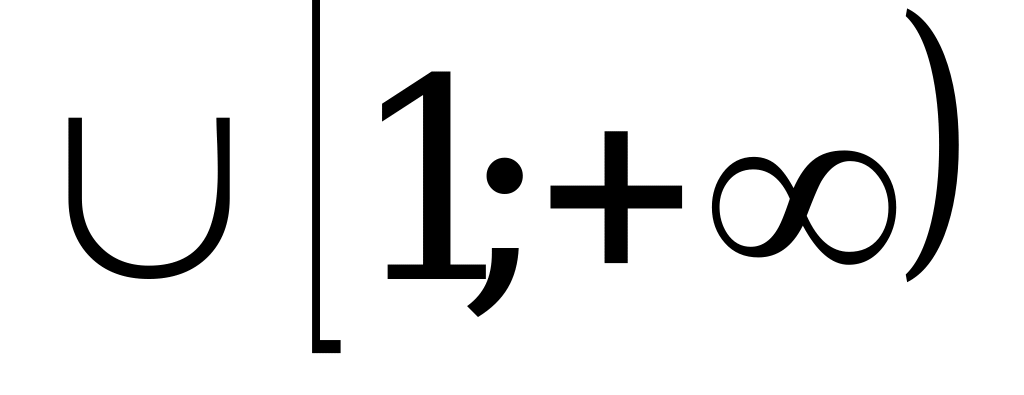,т.к. 0.

б) При переходе через точку х = 0 слева направо производная меняет знак

с плюса на минус, а при переходе через точку х = 1 – с минуса на плюс.

Значит, ; .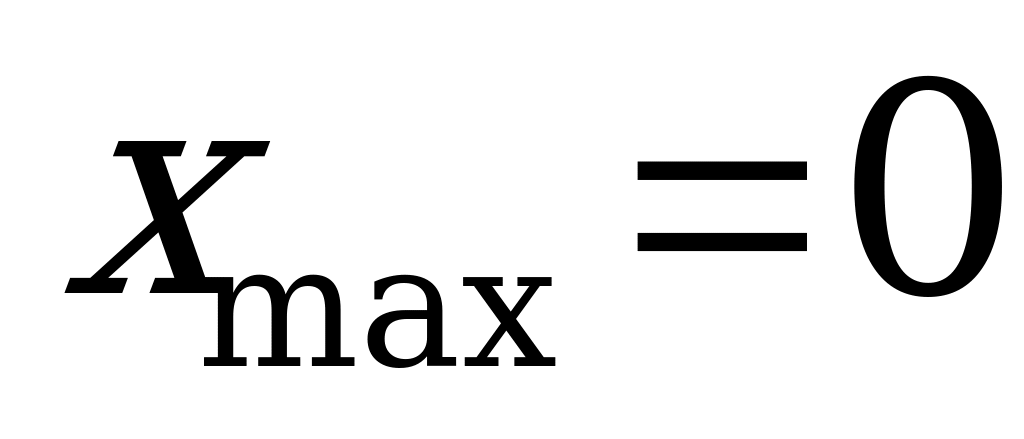

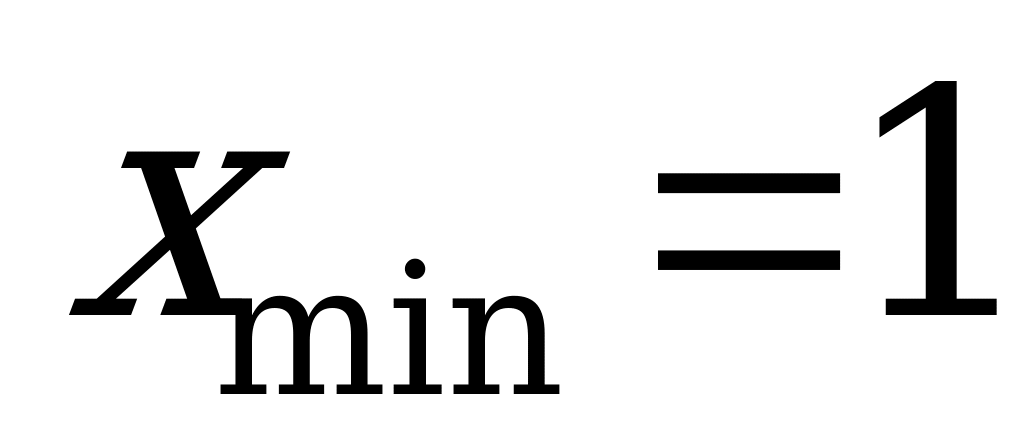Ответ: функция убывает при х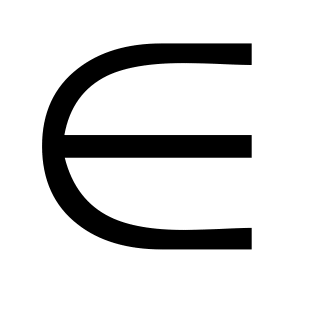 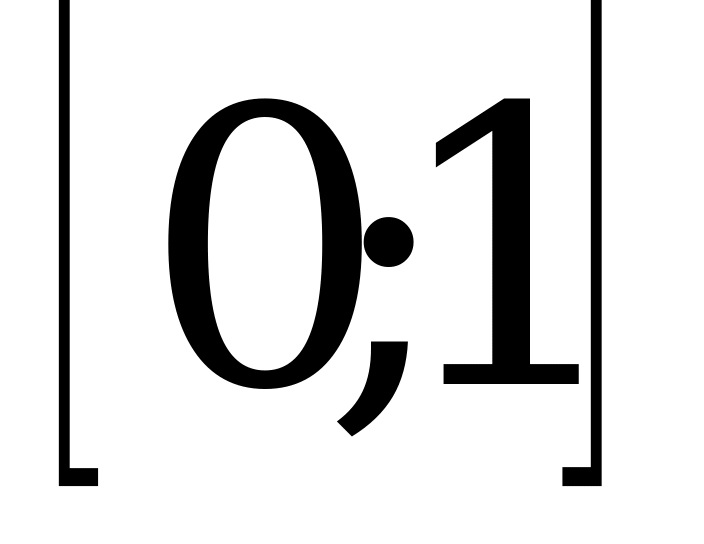, функция возрастает при х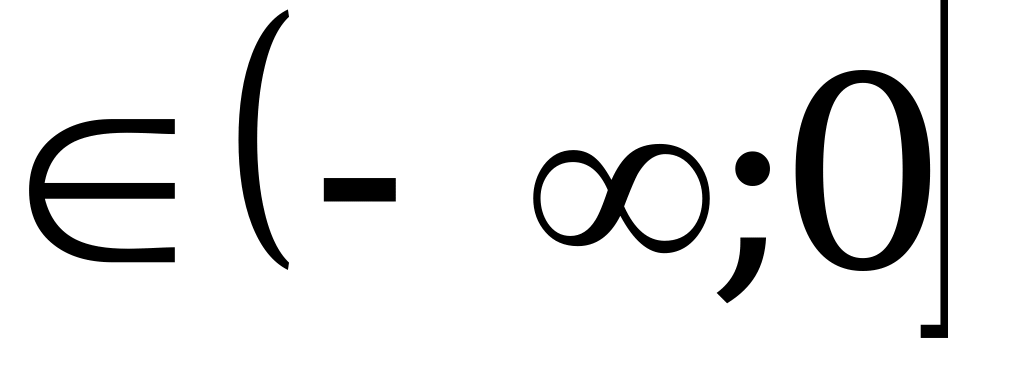 ; ; .
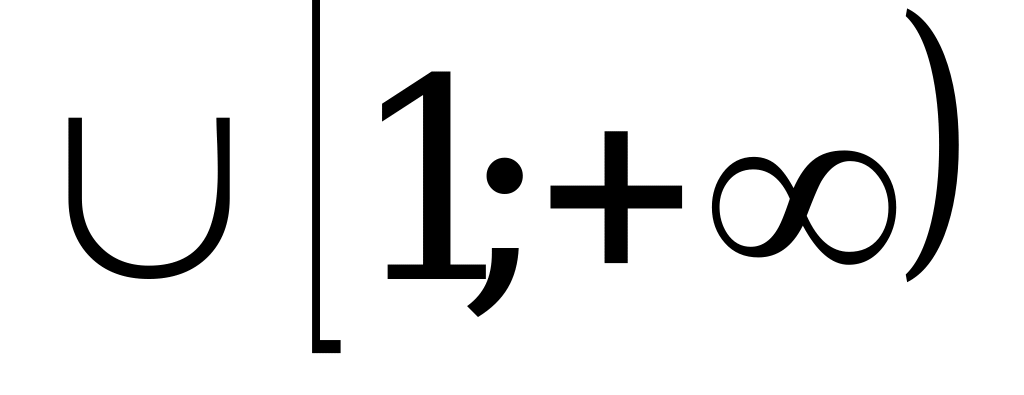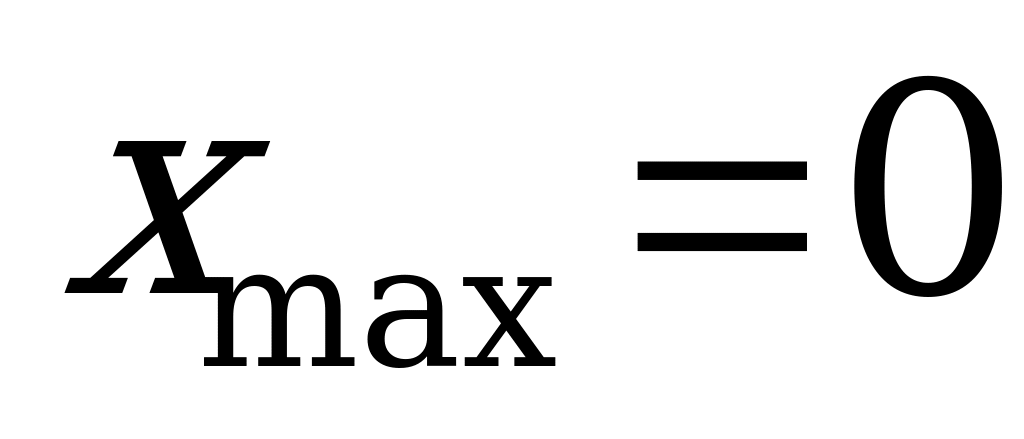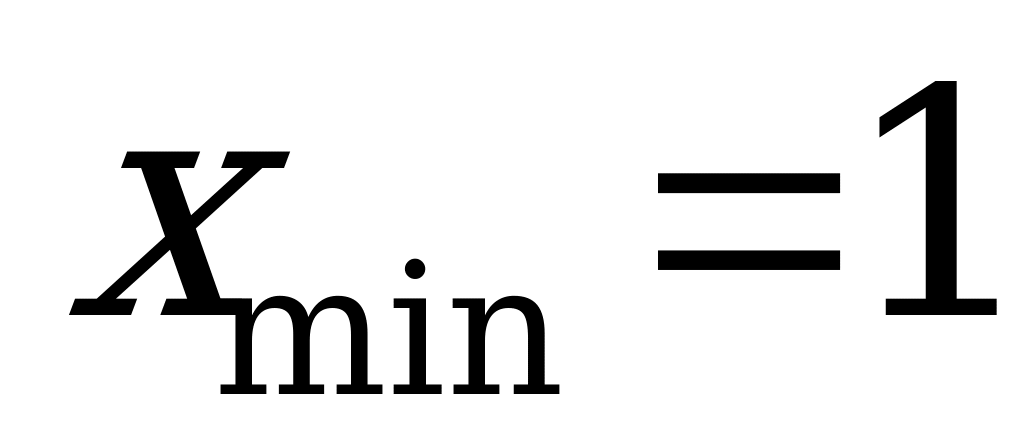