Тема «Свойства функции. Исследование функции»
Цель занятия: Обобщить знания по теме: «Функции и их свойства. Различные способы задания функций», выявить уровень овладения комплексом знаний по свойствам функции (область определения, четность, нечетность, периодичность, промежутки знакопостоянства и монотонности)
Задачи занятия:
Обучающие: повторение свойств функций; закрепление навыков исследования функций и построения их графиков;
Развивающие: развивать познавательный интерес к учебным дисциплинам и умение применять свои знания в практических ситуациях; расширить кругозор учащихся, повысить их интеллект; развивать логическое и критическое мышление.
Воспитательные: воспитывать культуру общения и культуру речи; воспитание чувства ответственности и солидарности.
Тип занятия: совершенствование знаний, умений и способов деятельности.
Материалы и оборудование: учебные пособия, мел, доска, карточки с самостоятельной работой
Технологическая карта занятия:
| Этап занятия | Деятельность преподавателя | Деятельность учащихся | Формы организации |
| Организационный момент | Проверка наличия учащихся на занятии. Объявление темы занятия | Подготовка к работе | Фронтальная |
| Проверка домашнего задания | Проверка наличия и правильности выполнения домашнего задания. Анализ типичных ошибок | Решение на доске заданий, вызвавших затруднения дома | Фронтальная, индивидуальная |
| Повторение опорных знаний | Организация фронтального и индивидуального опросов, комментирование ответов, координирование самостоятельной работы обучающихся (Приложение 1) | Ответы на вопросы преподавателя устно и на доске | Фронтальная, индивидуальная |
| Актуализация знаний | Решение тренировочных упражнений; пояснение фактов, вызвавших затруднения. Координирует рассуждения учащихся (Приложение 2) | Конспектирование решаемых упражнений, выяснение недопонятых моментов, ответы на вопросы преподавателя | Фронтальная, индивидуальная |
| Применение знаний на практике | Исследовательская работа. Корректирует недочеты. Организует самостоятельную работу учащихся. Индивидуальная помощь (Приложение 3) | Несколько учащихся у доски исследуют функцию по общей схеме, остальные работают самостоятельно, уточняя возможные несоответствия Самостоятельно проводят исследование функции с самопроверкой | Фронтальная, работа в малых группах |
| Закрепление знаний и способов деятельности | Ознакомление с ходом выполнения самостоятельной работы. Организует самостоятельную работу учащихся (Приложение 4) | Выполнение самостоятельной работы. | Индивидуальная |
| Домашнее задание | Инструктирует учащихся по выполнению домашней работы. | Записывают задания. Задают интересующие вопросы | Индивидуальная |
| Итоги занятия. Рефлексия | Организует фронтальную беседу, оценку результатов занятия (Приложение 5) | Высказывание собственного мнения, обобщение изученного | Фронтальная, индивидуальная |
Приложение 1
Фронтальный опрос.
1). Что такое функция?
2). Способы обозначения и задания функции.
4). Что такое область определения функции? Записать обозначение. Указать D(f) для нашей функции по графику.
5). Что такое область значений функции? Записать обозначение. Указать D(f) для нашей функции по графику.
6). Какая функция называется непрерывной на промежутке? Определи, будет ли наша функция непрерывна?.
7). Дополнить неуказанные свойства функции. Применить их для данной функции.
8). Какова зависимость между ограниченностью и наибольшим / наименьшим значениями функции?
9). Перечислить основные свойства функции.
Подводятся итоги по опросу. Отмечаются лучшие ответы
Приложение 2
Задача 1. Указать область определения функции: а) 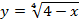 ; б)
; б) 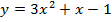 .
.
а) Т. к. функция представляет собой корень четной степени из выражения, содержащего неизвестную, то подкоренное выражение должно быть неотрицательным.
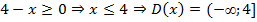 .
.
г) Указанная квадратичная функция 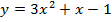 не имеет ограничений на область определения, т. к. функция будет иметь смысл при любых значениях аргумента, т. е.
не имеет ограничений на область определения, т. к. функция будет иметь смысл при любых значениях аргумента, т. е. 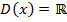 .
.
Задача 2. Указать область значений функции: а)  ; б)
; б) 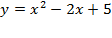 .
.
а) Получим ограничения на область значений данной функции путем преобразований ограничений на простейшую функцию 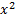 :
:
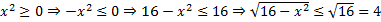
С другой стороны важно не забыть, что корень четной степени имеет неотрицательные значения, т. е.:
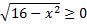
Таким образом, если учесть эти оба условия, то мы получим, что
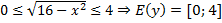 .
.
б) Мы уже обсуждали, что для определения области значений для квадратичной функции необходимо вычислить координату вершины ее параболы по оси ординат. Давайте вспомним из школьной программы как вычислить для начала иксовую координату вершины параболы:

Теперь найдем игрековую координату вершины, для этого подставим  в функцию:
в функцию:

Поскольку парабола имеет положительный старший коэффициент, то ее ветки направлены вверх, и 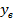 является ее минимальным значением, следовательно:
является ее минимальным значением, следовательно:
 .
.
На следующем уроке мы с вами еще подробно разберемся с определением вершины и построением параболы.
Задача 3. Определить тип четности функции: а) 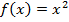 ; б)
; б)  .
.
Во всех случаях для определения типа четности функции необходимо подставить аргумент с противоположным знаком, т. е.  . Именно для того, чтобы это нагляднее продемонстрировать, мы и обозначили функции в виде
. Именно для того, чтобы это нагляднее продемонстрировать, мы и обозначили функции в виде 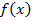 .
.
а)  - функция четная.
- функция четная.
б) 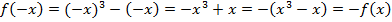 - функция нечетная.
- функция нечетная.
Ответ. а) функция четная; б) функция нечетная.
Задача №11. Указать промежутки монотонности функции, которая приведена на графике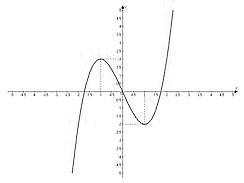
Функция возрастает там, где большему значению аргумента соответствует большее значение функции. Такие участки исходя из графика. 
Функция убывает там, где большему значению аргумента соответствует меньшее значение функции. Такие участки исходя из графика  .
.
Обратите внимание, что промежутки монотонности функции указываются именно для значений аргументов, т. е. иксов.
Ответ. Функция возрастает при  ; функция убывает при
; функция убывает при  .
.
И выполним чтение нескольких графиков функций. При этом нам необходимо будет указать основные характеристики и свойства функций.
Приложение 3
Дана функция у = f(х), где
f(х) =
1. Вычислить: а) f( -2), б) f ( 0), в) f( 1, 25), г) f(6).
2. Найти D (f) и E(f).
3. Выяснить, сколько корней имеет уравнение f(х) =а при различных значениях а.
4. Решить неравенства:
а) f(х)
б) f(х) 0,5.
Решение.
Дана кусочная функция.
1.а) значение х=-2 удовлетворяет условию -2 ≤ х ≤ 0, значит f( -2) надо вычислять по формуле f(х) =- х²; f( -2) = -(-2)² ==-4.
б) значение х =0 удовлетворяет условию -2 ≤ х ≤ 0, значит f ( 0) надо вычислять по формуле f(х) =- х²; f ( 0) =-0² =0.
в) значение f( 1, 25) удовлетворяет условию 0
г) значение f(6) удовлетворяет условию х 3, значит f(6) надо вычислять по формуле 3/х +1
f(6)=3:х +1= 3:6+1=1,5.
2. Область определения D (f) состоит из трех промежутков:
[-2;0], (0;3], (3; +∞). Объединив их, получим луч [-2; +∞).
Чтобы найти область значений функции, построим ее график. Он состоит из трех кусочков заданной функции. Спроецировав этот график на ось у, получим область значений функции.
E(f)= [-4; 0]U( 1; 2]
3. Выясним, сколько корней имеет уравнение f(х) =а при различных значениях а.
Для этого нужно определить, сколько точек пересечения имеет построенный график функции с прямой у=а при различных значениях параметра а.
1) При -4 ≤ а≤ 0 прямая пересекается с графиком в одной точке. Значит, уравнение имеет 1 корень.
2) При а
3) При 0
4) При а2 корней нет.
5) При а=2 1 корень.
6) При 1
4. Решим неравенство f(х)
f(х)0,5 при х0.
Приложение 4
Самостоятельна работа по теме «Свойства функции»
ВАРИАНТ 1.
Найти область определения функции 
1) 2)
2) 
3)  4)
4) 
2. Функции заданы формулами:
а)  б)
б)  в)
в)  г)
г) 
Какие из них являются возрастающими?
а и б 2) а и г 3) в и г 4) а, б и г
Какая из данных точек принадлежит графику функции  ?
?
А( - 6; 3) 2) В(8; 2) 3) С( -3; - 6) 4) D(2; - 8)
Найдите наименьшее значение функции 
4 2) 0 3) не существует 4) 8
Среди заданных функций укажите нечётные:
а)  б)
б)  в)
в)  г)
г) 
1) а и б 2) б и г 3) а и в 4) в и г
ВАРИАНТ 2.
Найти область определения функции 
1) 2)
2) 
3)  4)
4) 
2. Функции заданы формулами:
а)  б)
б)  в)
в)  г)
г) 
Какие из них являются убывающими?
а и б 2) а и в 3) в и г 4) а, б и г
Какая из данных точек принадлежит графику функции  ?
?
А( - 4; - 6) 2) В(- 6; 4) 3) С( 4; 8) 4) D(8; - 4)
Найдите наименьшее значение функции 
9 2) 0 3) не существует 4) 18
Среди заданных функций укажите чётные:
а)  б)
б)  в)
в)  г)
г) 
1) а и в 2) б и г 3) а и б 4) в и г
Приложение 5
Выполнить чтение графиков функций:
а)
1. Область определения 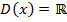 ;
;
2. Область значений  ;
;
3. Точки пересечения с осями: с осью ординат  ;
;
4. Т. к. все точки функции симметричны относительно оси ординат, то она четная;
5. Непериодичная;
6. Монотонно возрастает при  , монотонно убывает при
, монотонно убывает при  .
.
б)
1. Область определения  ;
;
2. Область значений ;
;
3. Точки пересечения с осями: с осью абсцисс  ;
;
4. Т. к. нет симметрии, то функция общего вида;
5. Непериодичная;
6. Монотонно возрастает при  , монотонно убывает при
, монотонно убывает при  .
.






























